y35 Εz
Cross-Sectional Effects of Common and Heterogeneous Regressors on Asymptotic Properties of Panel Autoregressive Unit Root Tests
Katsuto Tanaka
Faculty of Economics, Gakushuin University, Tokyo, Japan
The present paper deals with nonstationary panel autoregressive iARj models, and examines cross-sectional effects of regressors on the asymptotic properties of panel unit root tests for the ARi1j coefficient. We consider various types of common and heterogeneous regressors and compute limiting local powers of tests as T ¨ for each N, where T and N are the time and cross section dimensions, respectively. Dealing with tests based on the ordinary least squares estimator iOLSEj and the generalized LSEiGLSEj, we examine how common and heterogeneous regressors affect the tests as N becomes large. It is shown that the existence of common regressors does not affect the tests asymptotically as N ¨. This means that the power of the tests remains the same even if the model contains common regressors. We further derive the limiting power envelopes of the most powerful invariant iMPIj tests, which yields the conclusion that the GLSE-based tests are asymptotically efficient, unlike the time series case.
Keywords Asymptotically efficient test, Common regressor, Cross-sectional effect, Heterogeneous regressor, Moment generating function, Numerical integration, Panel unit root tests.
Address correspondence to Katsuto Tanaka:
Faculty of Economics
Gakushuin University
Mejiro, Toshima-ku, Tokyo 171-8588
Japan
e-mail: ![]()
1. INTRODUCTION
Nonstationary panel AR models were extensively discussed in Moon and Perron i2008j and Moon, Perron, and Phillipsi2007j, where the former deals with the case of heterogeneous intercepts, whereas the latter discusses the case of heterogeneous trends. In these papers, the limiting local powers of various panel AR unit root tests are computed as T and N jointly tend to under the local alternative that shrinks to the null at the rate of 1/iTNΘj, where T is the time series dimension and N is the cross section
y36
Εz
dimension with 0 Θ 1.
@@Unlike the above works, the present paper examines the effect of the cross section dimension N on the unit root tests as T ¨. This may be useful when T is bigger than N and it is desirable to see the intermediate situation rather than the final situation as both T and N go to . We consider four types of regressors:i1j a common intercept and trend,i2j heterogeneous intercepts and a common trend,i3j a common intercept and heterogeneous trends, i4j heterogeneous intercepts and trends. For these models we conduct panel unit root tests based on the OLSE and GLSE of the AR coefficient, and some other tests based on these residuals. To see the cross-sectional effect, we compute limiting local powers of
these unit root tests as T ¨ for each intermediate N under the AR coefficient close to unity in the order of 1/T. It is theoretically and graphically shown that, as N becomes large, the existence of common regressors does not affect the asymptotic properties of these tests, although that of heterogeneous regressors does affect. This fact was also partly observed in panel AR models discussed in Breitung i2000j and Moon et al.i2007j. We give more detailed analysis of this fact for each intermediate value of N. We also derive the limiting powers of these tests and envelopes of the most powerful invariant iMPIj tests as N ¨, utilizing the joint moment generating functions im.g.f.sj associated with the test statistics obtained in Nabeya and Tanakai1990j, Tanakai1996, Chap. 7j, and Tanakai2017, Chap. 10j.
@@The outline of the paper is as follows. In Section 2 we present panel AR models to be dealt with in this paper. In Section 3 we compute limiting local powers of various unit root tests. In Section 3.1 we deal with OLSE-based tests, followed by GLSE-based tests in Section 3.2. The limiting power envelopes are derived in Section 3.3, and it is found that the GLSE-based tests are asymptotically efficient, unlike the time series case. The effect of temporal or cross-sectional dependence of the error term on the tests is discussed in Section 3.4. Section 4 concludes the paper. Proofs of theorems are provided in the Appendix.
2. PANEL AR MODELS
The panel AR models to be discussed in this paper are the following types:

where i refers to cross section, whereas t refers to time series. The processoΕit p is defined for all models by
y37 Εz

where it is assumed thatoΕit p starts from Εi0 0 for each i, and is driven byoΓit p. We initially assumeoΓit p` i.i.d.i0, Π2 j for simplicity of presentation. The case of temporal or cross-sectional dependence will be discussed in Section 3.4.
Model A is the most restricted model with common intercept and trend. Model B has heterogeneous intercepts, whereas Model C has heterogeneous trends. Model D is the most unrestricted model with heterogeneous intercepts and trends. Note that these four models coincide with each other when N1.
@@For the above models we consider the panel AR unit root test

where we assume that, under H1, Οi takes the following form:

with c 0 and 0 Θ 1. This is a simple extension of the time series unit root test. A more general alternative allows the true value of Οi to be different among cross sections. Moon and Perroni2008j and Moon, Perron, and Phillips i2007j assume such an alternative, but we maintain i7j to simplify subsequent discussions.
@@Under the above setting we shall explore asymptotic properties of various unit root tests. For this purpose we define the Ornstein-UhlenbeckiO-Uj process by
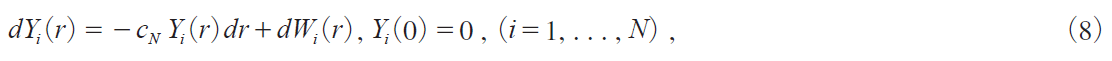
where r Έ m0, 1n and oWi irjp is the standard Brownian motion independent of oWkirjpiikj so that Y1 irj, . . . , YN irj are i.i.d. for any r Έm0, 1n.
3. LIMITING POWERS AND POWER ENVELOPES
We first compute the limiting local powers of various unit root tests for Models A through D. In Section 3.1 we deal with OLSE-based tests, followed by GLSE-based tests in Section 3.2. The limiting power envelopes of the MPI tests are derived in Section 3.3. The effect of temporal or cross-sectional dependence of the error term is discussed in Section 3.4.
3.1. OLSE-Based Tests
The present test was earlier considered in Moon et al. i2007j, and Moon and Perron i2008j. The limiting local power was also computed in these works as both T and N go to under a more general setting. Here we examine the cross-sectional effect of regressors as T ¨ for each N.
y38 Εz
Let ![]() itiM jbe the OLS residual obtained from Model M iMA, B, C, Dj. Then we compute the estimator
itiM jbe the OLS residual obtained from Model M iMA, B, C, Dj. Then we compute the estimator ![]() iM j of Οi Ο under H0 by
iM j of Οi Ο under H0 by
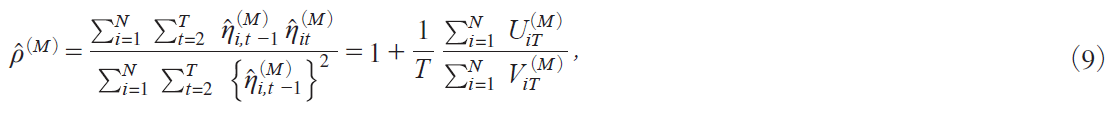
where
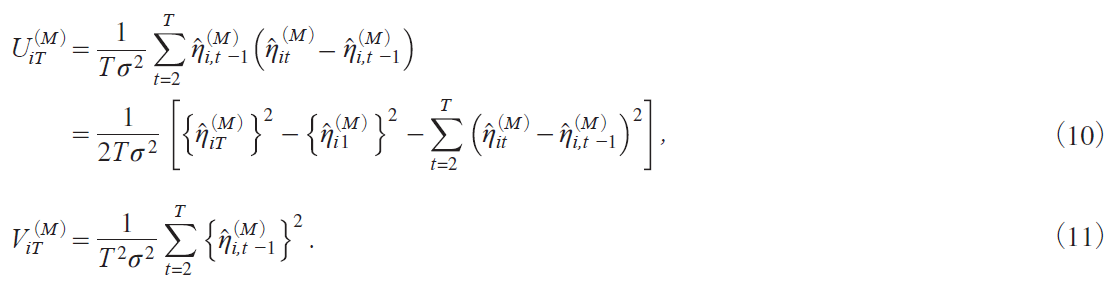
@The following theorem describes the asymptotic distribution of ![]() iM j as T ¨ for each N, the proof of which is given in the Appendix.
iM j as T ¨ for each N, the proof of which is given in the Appendix.
Theorem 1. As T ¨ with N fixed under Οi 1|cN / T , the asymptotic distribution of ![]() iM j in Model M iMA, B, C, Dj follows
iM j in Model M iMA, B, C, Dj follows
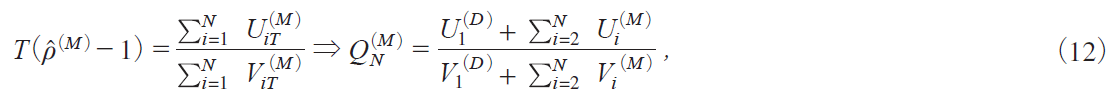
where
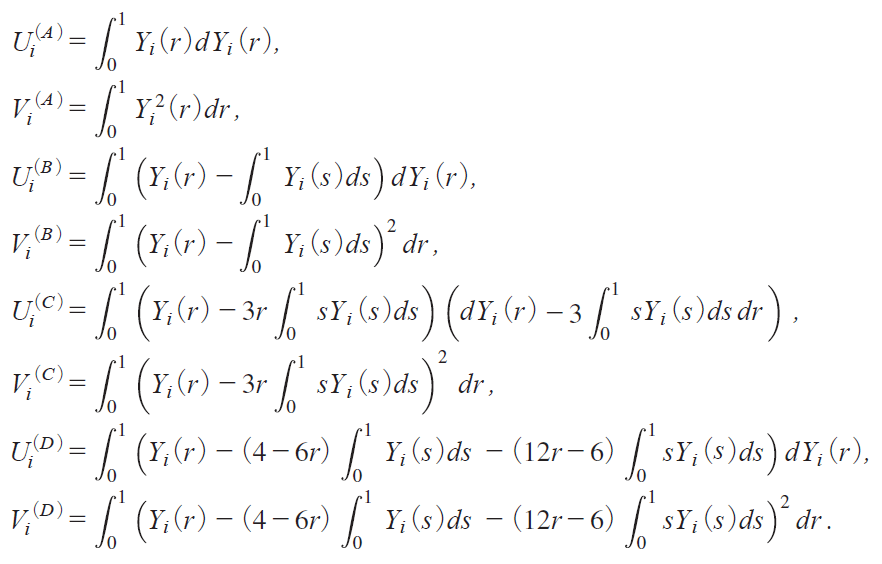
y39 Εz
@Some remarks follow.
iaj When N1, that is, in the time series case, the distribution of QNiM j in i12j reduces to Q1iD jU1iD j/V1iD j for all M. Note also that U1iA j/V1iA j corresponds to the popular near-unit root distribution associated with the time series model xtΟxt|1{Γt with Ο1|c/T .
ibj As N becomes large, it holds that
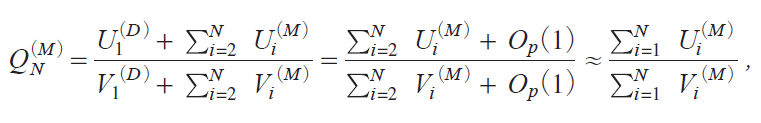
where the distribution of this last quantity is obtained from Model M without common regressors, which means that the effect of common regressors fades away as N becomes large.
icj We can deal with some other variations of the above models, for which we can also consider the
statistics T i![]() iEj|1j. For example, we can show that, as T ¨ with N fixed under Οi 1| cN /T ,
iEj|1j. For example, we can show that, as T ¨ with N fixed under Οi 1| cN /T ,
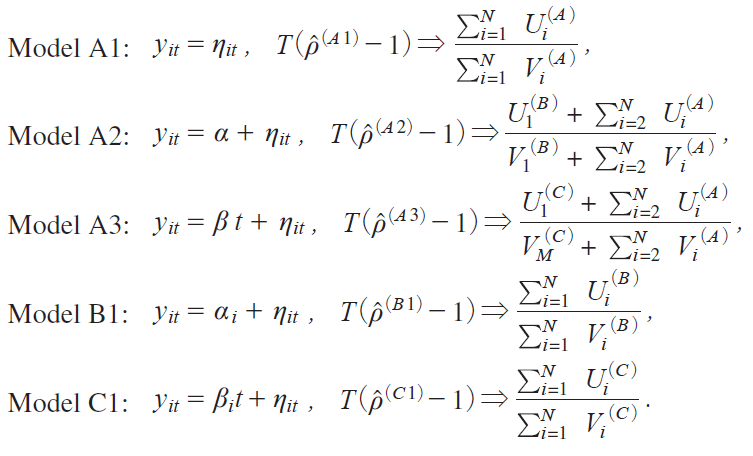
Thus we also conclude that, for these models, the existence of common regressors does not affect the asymptotic behavior of the OLSE-based tests as N ¨, which was also described inibj.
idj Ui iC j and Vi iC j behave differently from the other quantities, which may be because Ui iC j/Vi iC j results from the restricted regression without intercept yit ΐi t{Εit . It can also be shown that Ui iM j and Vi iM j are uncorrelated under Ο1 for MB, D, but are correlated for MA, C. In fact, it holds that CoviUi iA j, Vi iA jj1/3 and CoviUi iC j, Vi iC jj1/175 when cN0. These can be computed easily from the joint moment generating functionim.g.f.j described below.
To compute the distribution of QNiM j in i12j for each N, we use the joint m.g.f.miM jix, y j of Ui iM j and Vi iM j defined by
y40 Εz
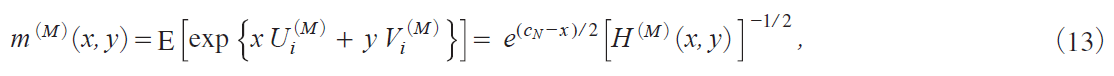
where, by putting Κ 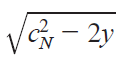 , we havemTanakai2017, Chap. 10jn
, we havemTanakai2017, Chap. 10jn
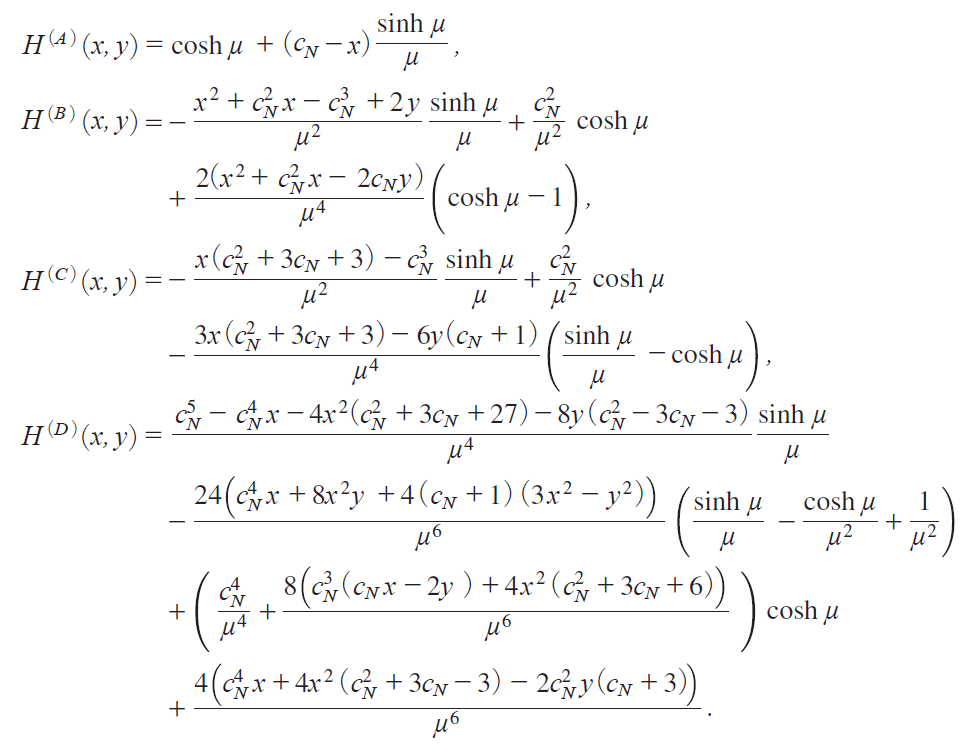
Then the distribution of QNiM j can be computed by using Imhoffs formulamImhof i1961jn
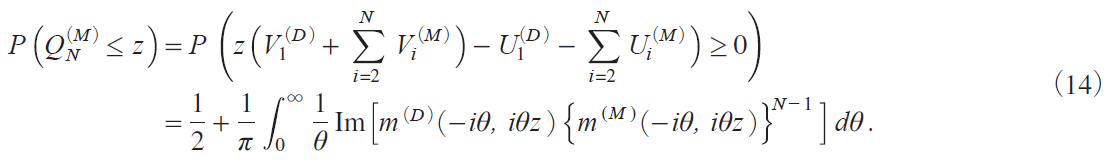
Numerical computation like Simpsonfs formula can be used to compute i14j by taking care of the computation of square roots of complex-valued quantitiesmTanakai1996jn.
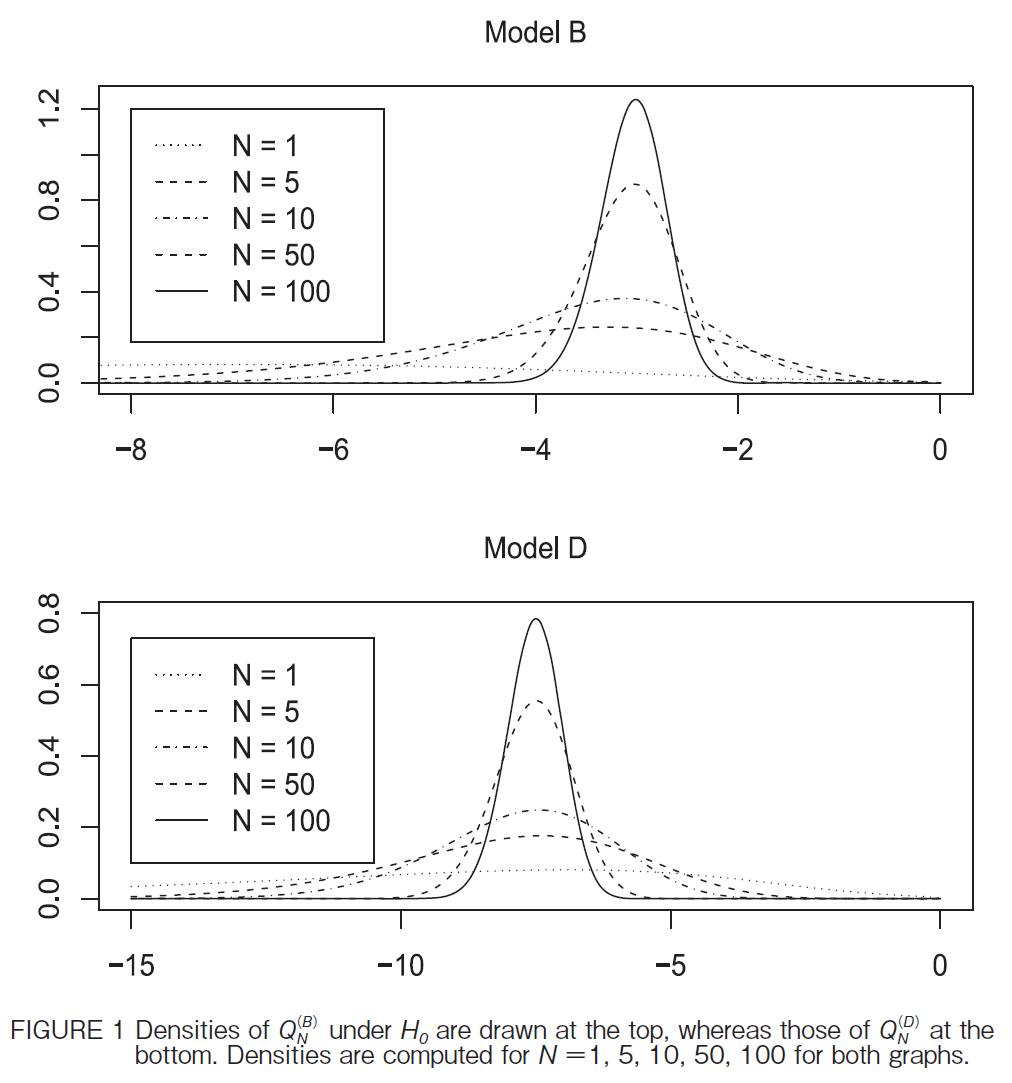
@@Figure 1 draws the probability densities of QNiB j and QNiD j for various values of N under H0icN0jto examine the cross-sectional effect of N. As Theorem 2 below indicates, these distributions converge to |3 and |15/2, respectively, as N becomes large. Note that Q1iB jQ1iD j. The distributions QNiB j for N 1 are shifted from Q1iD j, whereas QNiD j for N 1 are just the convolution since P iQNiD j≤ z jPi![]() izVi iD j|Ui iD jj≥0j, as is seen fromi14j. The general feature of QNiA j and QNiC j are the same as QNiB j, although those densities are not presented here.
izVi iD j|Ui iD jj≥0j, as is seen fromi14j. The general feature of QNiA j and QNiC j are the same as QNiB j, although those densities are not presented here.
@@We next compute limiting powers of the tests based on QNiM j as N ¨ under Ο1|cN with cN y41 Εz c/NΘ. We need to find the limiting distribution of normalized QNiM j by suitably choosing Θ. For this purpose, let us put
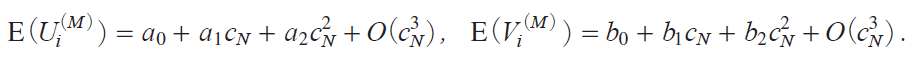
The joint m.g.f. miM jix, y j of Ui iM j and Vi iM j shown above can be used to compute these moments using the Taylor expansion, as is shown in the Appendix. We have, by the week law of large numbersiWLLNjand the central limit theoremiCLTj,
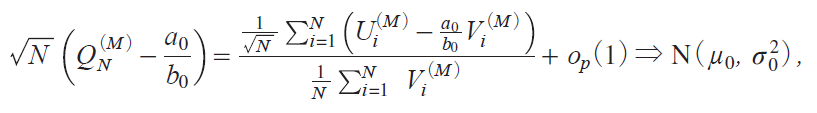
y42 Εz
where
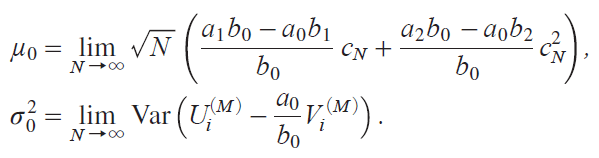
Then it is recognized that, for the asymptotic distribution of normalized QNiM j to be nondegenerate, cNOi1/![]() j when a1b0|a0b10, and cNOi1/N 1/4j when a1b0|a0b10 and a2b0|a0b20. It is shown in the Appendix that cNOi1/
j when a1b0|a0b10, and cNOi1/N 1/4j when a1b0|a0b10 and a2b0|a0b20. It is shown in the Appendix that cNOi1/![]() j for QNiA j and QNiB j , whereas cNOi1/N 1/4j for QNiC j and QNiD j, and we have the the following theorem.
j for QNiA j and QNiB j , whereas cNOi1/N 1/4j for QNiC j and QNiD j, and we have the the following theorem.
Theorem 2. The limiting powers of the tests based on QNiM jiMA, B, C, Dj under Ο1| c /iNΘT j at the 100Α% level are given as follows:
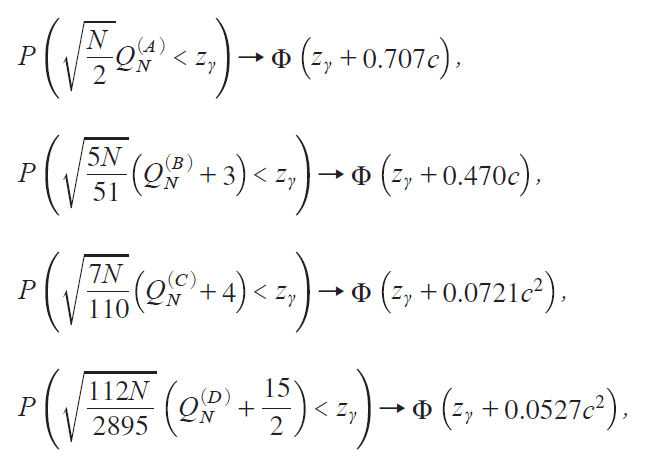
where ³iEj is the distribution function of Ni0, 1j, and zΑ is the 100Α% point of Ni0, 1j, whereas Θ1/2 for Models A and B, and Θ1/4 for Models C and D.
@@It follows that the OLSE-based unit root tests in Models A and B have nontrivial powers in a N |1/2T |1 neighborhood of unity, whereas the powers for Models C and D are nontrivial in a N |1/4T |1 neighborhood of unity. It is also seen that the limiting power decreases as the model complexity increases.
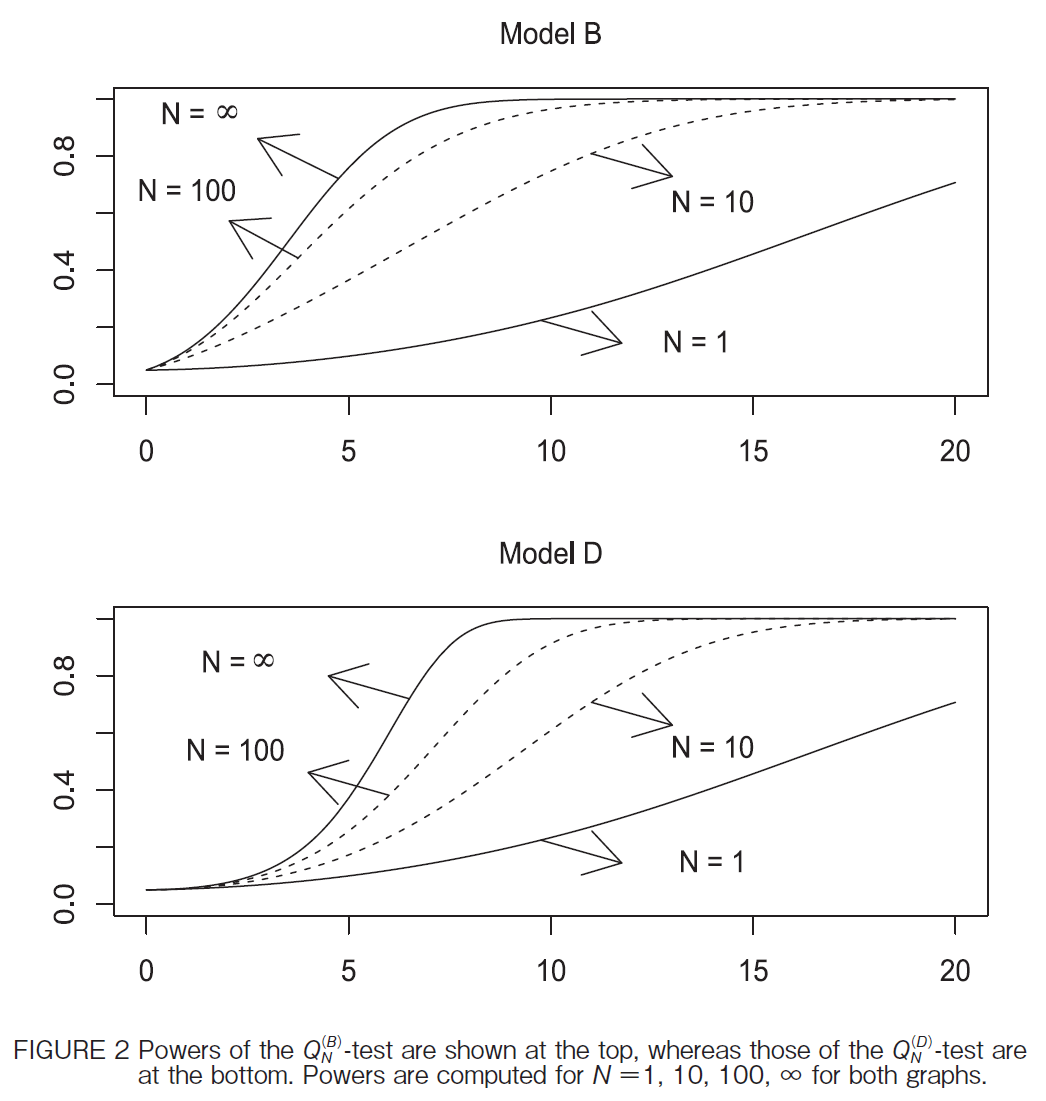
Figure 2 shows powers of the QNiB j - and QNiD j -tests against ccN NΘΈm0, 20n at the 5% level for N1, 10, 100, , where the powers for N are obtained fromi14j by putting z at the 5% point of the null distribution of QNiM j, whereas those for N are obtained from Theorem 2. It seems that the powers for N100 are still not well approximated by the limiting powers. This is particularly true of Model D. The powers of the QNiB j -test are higher than those of the QNiD j -test, which is also evident from Theorem 2. This means that the existence of heterogeneous trends decreases the power.
@@In the next subsection we consider the GLSE-based tests, which will be shown to be better than the
y43 Εz
OLSE-based tests.
3.2.GLSE-Based Tests
Let us express Model M iMA, B, C, Dj as y X iM jΑiM j{Ε, where X iM j and ΑiM j are the regression matrix and parameter vector in Model M, respectively, whereas
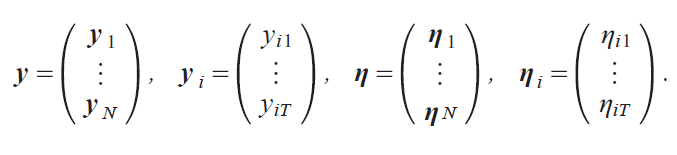
y44 Εz
Then we define the GLS residual by ![]() iM jy | X iM j
iM jy | X iM j![]() iM j, where
iM j, where
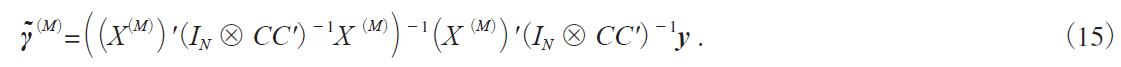
Here ⊗ is the Kronecker product and C is the T ~ T lower triangular matrix with is, t j-th element
being 1 for s ≥ t and 0 otherwise. The GLSE ![]() iM j of Ο can be computed followingi9j with
iM j of Ο can be computed followingi9j with ![]() iM j replaced by
iM j replaced by ![]() iM j.
iM j.
@@The following theorem describes the asymptotic distribution of ![]() iM j as T ¨ for each N, the proof of which is given in the Appendix.
iM j as T ¨ for each N, the proof of which is given in the Appendix.
Theorem 3. As T ¨ with N fixed under Ο1| cN /T , the asymptotic distribution of ![]() iM j for Model M iM A, B, C, Dj follows
iM j for Model M iM A, B, C, Dj follows

where
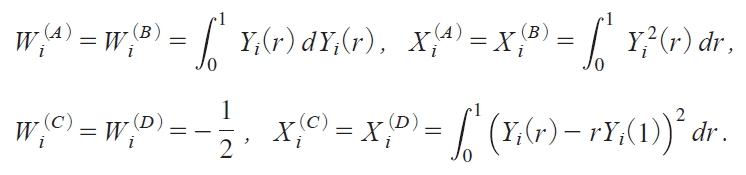
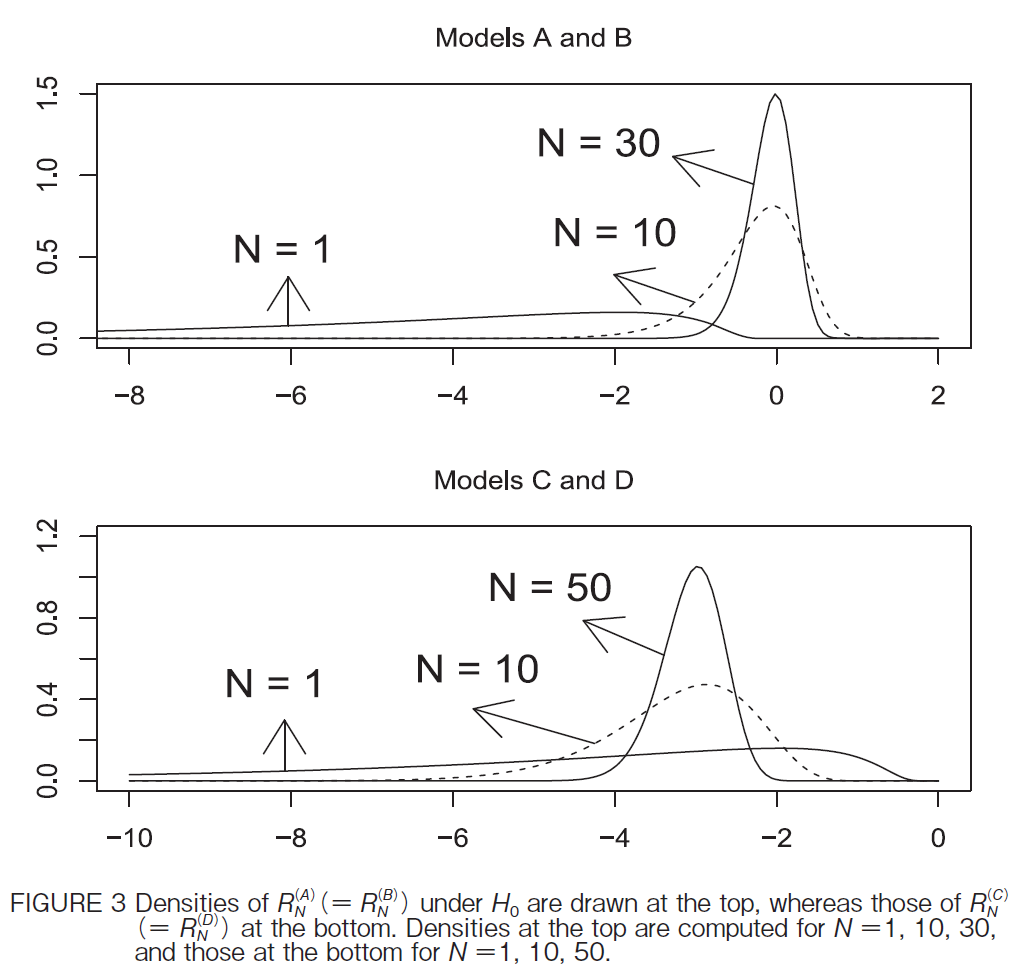
@@It is noticed that the distributional structure of the GLSE-based statistics RNiM j remains the same as that of the OLSE-based statistics QNiM j. It is also seen that RNiA j coincides with RNiB j. The same is true of RNiC j and RNiD j, and these properties are also shared in the time series casemTanakai1996jn. The densities of RNiA ji RNiB jj under H0 are drawn at the top of Figure 3 for N1, 10, 30, whereas those of RNiC jiRNiD jj at the bottom for N1, 10, 50. The former densities are seen to be shifted from the latter as N becomes large. Both RNiA j and RNiB j converge to 0, whereas both RNiC j and RNiD j converge to |3, as is described in Theorem 4 below.
@@We next consider limiting powers of the tests based on RNiM j as N ¨ , which is described in the following theorem, the proof of which is given in the Appendix.
Theorem 4. The limiting powers of the tests based on RNiM jiMA, B, C, Dj as N ¨ under Ο1|c /iNΘT j at the 100Α% level are given as follows:
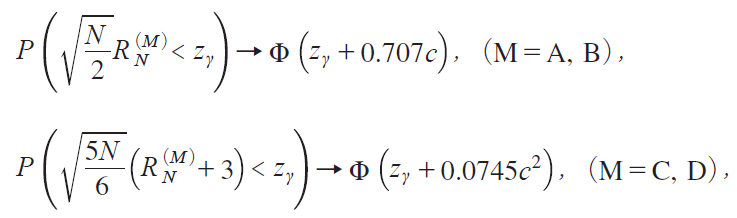
y45 Εz
where Θ1/2 for Models A and B, and Θ1/4 for Models C and D.
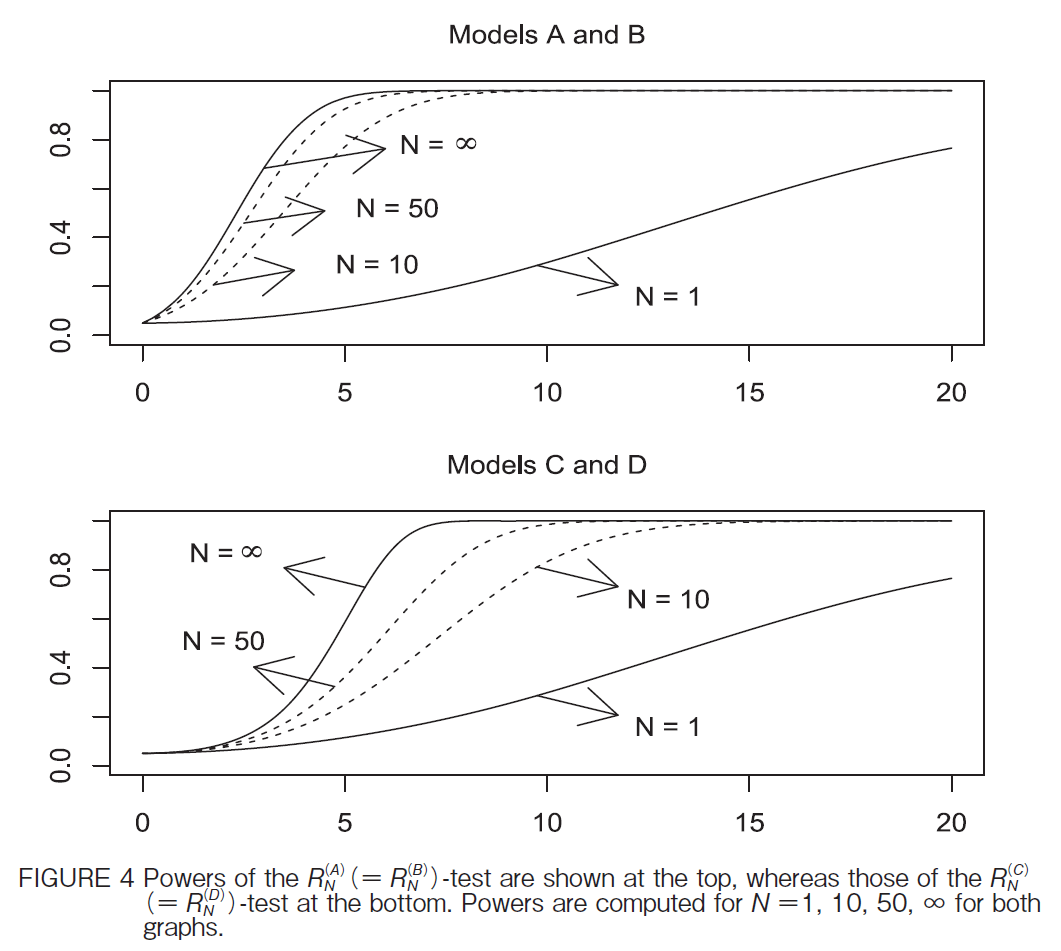
@@It follows from Theorem 4 that RNiM j converges to 0 for M A, B, whereas it converges to |3 for MC, D, as was mentioned before. It is also noticed from Theorems 4 and 2 that the GLSE-based tests are better than the OLSE-based tests in Models B, C, D, although those are the same in Model A. The top of Figure 4 shows powers of RNiA jiRNiB jj-tests at the 5% level for N1, 10, 50, , whereas the bottom of Figure 4 those of the RNiC ji RNiD jj-tests. It is seen that, for Models A and B, the powers for N50 are reasonably well approximated by the limiting powers, whereas, for Models C and D, the aprroximation is still not good enough for N50. It is seen that the former powers are higher than the latter, as is anticipated from Theorem 4. This means that the existence of heterogeneous trends decreases the power, as in the OLSE-based tests.
y46 Εz
3.3. Limiting Power Envelopes
In previous subsections, dealing with Models A through D, we considered panel unit root tests based on OLSE and GLSE, for which the limiting local powers were computed and power comparisons were made among those tests, examining the cross-sectional effects. In this subsection we derive the power envelopes, from which the performance of these tests can be evaluated. The idea was earlier developed in the time series context by Elliott et al. i1996j, and was extended to the nonstationary panel data by Moon et al. i2007j. Here we derive the power envelopes for Models A through D, paying attention to the cross-sectional effects.
@@Let us consider the testing problem
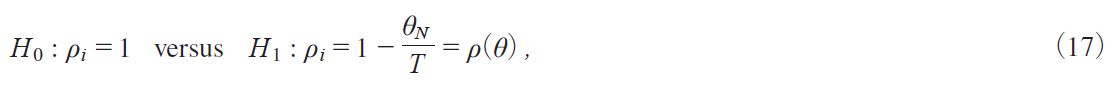
where ΖN Ζ/NΘ with Ζ being a known positive constant. We assume that the true value of Ο under H1 is y47 Εz given by Οicj1|cN /T with cNc/NΘ. AssumingoΓit p` NIDi0, Π2j, the Neyman-Pearson lemma tells us that the test which rejects H0 for small values of
is MPI, where ![]() itiM ji0j and
itiM ji0j and ![]() itiM ji1j are the GLS residuals obtained from Model M under H0 and H1, respectively. The residual
itiM ji1j are the GLS residuals obtained from Model M under H0 and H1, respectively. The residual ![]() itiM ji0j is the same as the GLS residual dealt with in the last subsection, that is,
itiM ji0j is the same as the GLS residual dealt with in the last subsection, that is, ![]() iM ji0j
iM ji0j![]() iMj, whereas
iMj, whereas ![]() iM ji1jy | X iM jΑiM ji1j, where
iM ji1jy | X iM jΑiM ji1j, where
with ΆiΖjIN ⊗ CiΟiΖjjC'iΟiΖjj. Here CiΟiΖjj is the T ~ T lower triangular matrix withis, T j-th element being Ο|s-t|iΖj for s ≥ t and 0 otherwise. The test based on SNTiM jiΖj with fixed Ζ is called the point optimal invariantiPOIj testmKingi1987jn.
@@The following theorem gives the weak convergence of SNTiM jiΖj as T ¨ for each N, the proof of which is given in the Appendix.
Theorem 5. As T ¨ under Ο1| cN /T for each N, the MPI test statisticSNTiM jiΖj ini18j follows
where
with ΒN 1{ΖN {![]() Ζ2N .
Ζ2N .
@@It is seen that the expression for SNiM jiΖj ini19j is of a similar nature to QNiM j ini12j and RNiMj in i16j. It is also noticed that the distribution of SNiM jiΖj depends on Ζ that is the value under H1. Thus the MPI test based on SNiM jiΖj is not uniformly best, but we can modify SNiM jiΖj so that the distribution of the modified statistic does not depend on Ζ as N ¨. Then we can compute the limiting power of the test based on a modified statistic which yields the limiting power envelope of all the invariant tests for Model M. The following theorem gives such statistics and the power envelopes.
y48 Εz
Theorem 6. The limiting powers of the tests based on the MPI statistics SNiM jiΖj ini19j at the 100Α% level as N ¨ under ΖN Ζ/NΘ and cNc/NΘ are given by
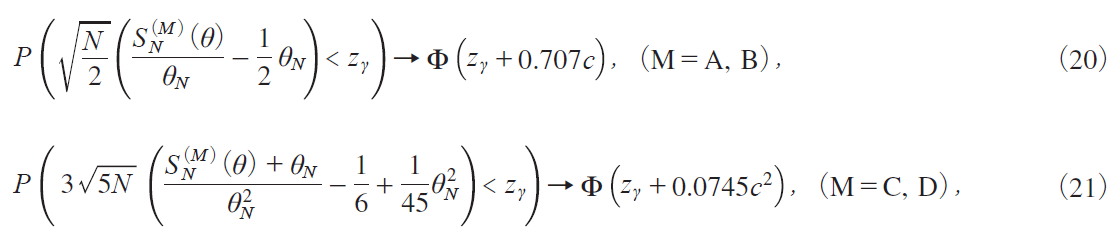
where Θ1/2 for Models A and B, and Θ1/4 for Models C and D.
@@The limiting powers of the modified tests give the power envelope of all the invariant tests. Comparing Theorem 6 with Theorem 4 it is seen that the power functions of the GLSE-based tests coincide with the power envelopes. Thus the GLSE-based tests are asymptotically efficient, unlike the time series case. This is a merit of panel tests as N ¨.
@@There are some other tests that are asymptotically efficient. Here we take up two such tests. Define
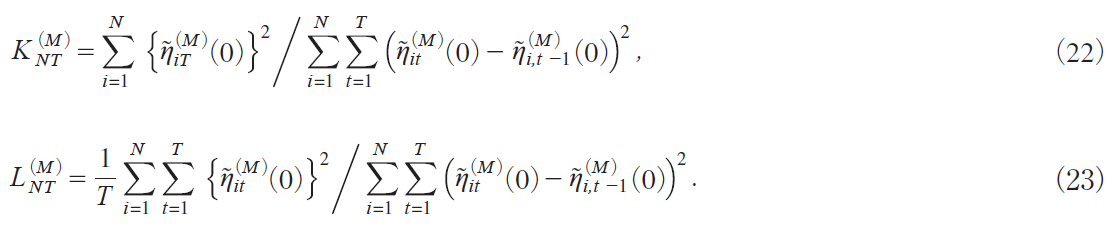
The test that rejects H0 for KNTiM j small is locally best invariantiLBIj, although the test is inapplicable to Models C and D because KNTiM j ί 0 for M C, D, whereas the test that rejects H0 for LNTiM j small is LBI and unbiasediLBIUj for MC,D mTanakai2017, Chap. 10jn. We have, as T ¨ for each N,
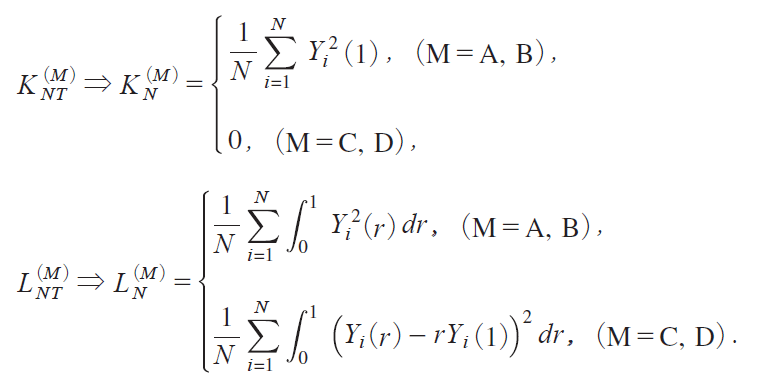
Since it can be shown that, for MA, B,
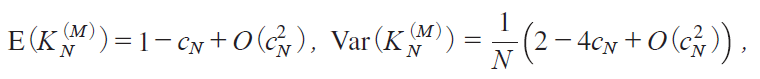
we have ![]() iKNiM j|1j Λ Ni|c, 2j by putting cNc /
iKNiM j|1j Λ Ni|c, 2j by putting cNc /![]() , which implies that the KNiM j-tests for MA, B are asymptotically efficient. It is evident that the LNiM j-tests are asymptotically efficient for MC, D.
, which implies that the KNiM j-tests for MA, B are asymptotically efficient. It is evident that the LNiM j-tests are asymptotically efficient for MC, D.
y49 Εz
Note that the LBI and LBIU tests in the time series caseiN1j are asymptotically inefficientmTanaka i1996, Chap. 9jn. We also note in passing that, if the GLS residual in i23j is replaced by the OLS residual, the resulting statistic is essentially the Durbin-Watson statistic and the corresponding test is asymptotically inefficient.
3.4. Effect of Temporal or Cross-Sectional Dependence
Here we consider the situation where there exists temporal or cross-sectional dependence of the error term oΓit p in i5j and examine the effect of such dependence on the test statistics obtained in previous subsections.
@@Let us first consider temporal dependence. For this purpose we assume
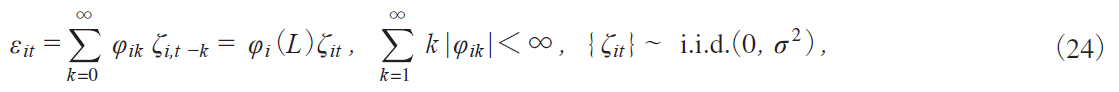
where Σi iLj1{Σi 1L{Σi 2L 2{E E E with L being the lag-operator. The distributional properties of the statistics T i![]() iM j|1j in i12j and T i
iM j|1j in i12j and T i![]() iM j|1j in i16j are affected by this relaxation. In fact, it can be shown that, as T ¨ for each N,
iM j|1j in i16j are affected by this relaxation. In fact, it can be shown that, as T ¨ for each N,
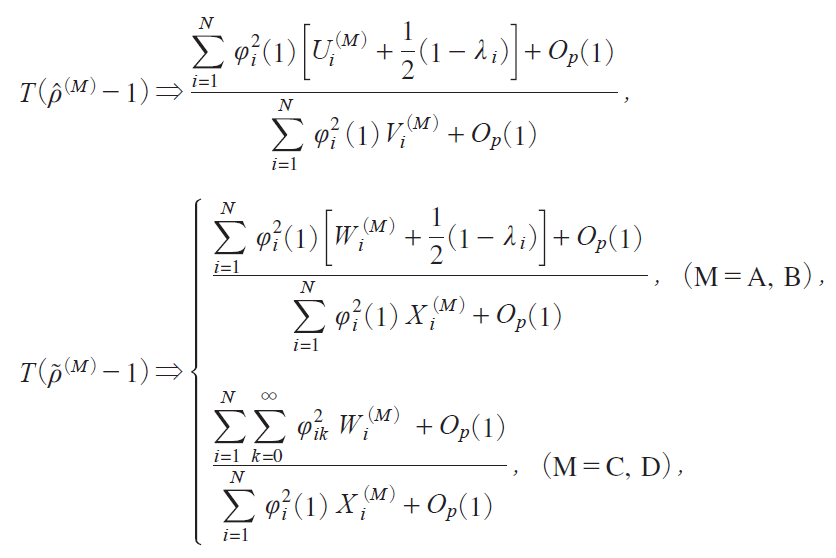
where Ui iM j and Vi iM j are defined in i12j, and Wi iM j and Xi iM j are defined ini16j, whereas Ιi is the ratio of the short-run to long-run variances of oΓit p given by![]() i1j. The above statistics depend on the short-run and long-run variances of the error term that characterize temporal dependence.
i1j. The above statistics depend on the short-run and long-run variances of the error term that characterize temporal dependence.
@@We next consider cross-sectional dependence, for which we assume that
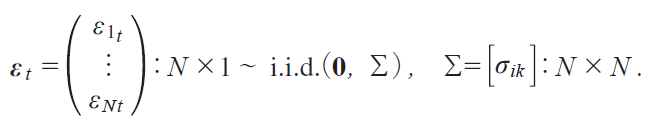
@It then follows that
y50 Εz
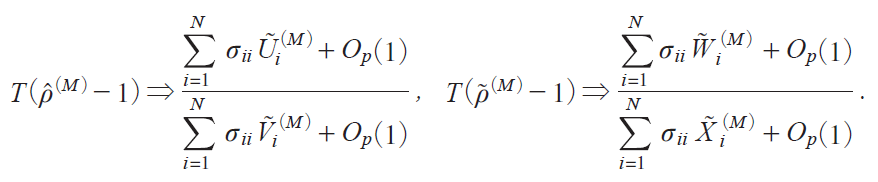
Here ![]() iiM j,
iiM j, ![]() iiM j,
iiM j, ![]() iiM j, and
iiM j, and ![]() iiM j replace Ui iM j, Vi iM j, Wi iM j, and Xi iM j, respectively, with Yi irj replaced by
iiM j replace Ui iM j, Vi iM j, Wi iM j, and Xi iM j, respectively, with Yi irj replaced by ![]() iirj, where
iirj, where
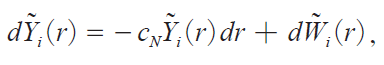
and o![]() iirjp is the standard Brownian motion with
iirjp is the standard Brownian motion with
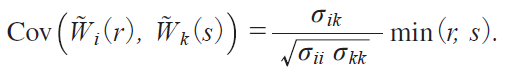
The test statistics depend on the covariances Πik of the error term that characterize cross-sectional dependence.
@@It is recognized from the above observations that, to use the asymptotic results obtained in previous subsections, we need to modify the statistics to make them independent of nuisance parameters. This remains to be done.
4. CONCLUDING REMARKS
Under a simple setting, we have presented a unified approach to deriving the limiting local powers of panel AR unit root tests, paying attention to the cross-sectional effect of N. For this purpose it is necessary to compute moments up to the second order of the limiting statistic in the time series direction. We found it easier to use its m.g.f., unlike in the literature. It happened that the tests that were not powerful in the time series case become more powerful in the panel case. It was also found that the existence of a common intercept and/or a common trend does not affect the asymptotic behavior of the tests. This holds for not only the tests based on OLS and GLS residuals, but also power envelopes.
@@The present approach can be applied to unit root tests for other types of panel models such as panel moving average models or panel error components models. Some simple extensions are found in Tanaka i2017, Chap. 10j. For these models the panel LBI or LBIU tests can be used and the corresponding statistics have a distributional structure similar to the panel AR unit root tests discussed in this paper. Details are reported in Tanakai2018j.
5. APPENDIX: PROOFS OF THEOREMS
Proof of Thereom 1: We first deal with Model D. Given the OLSEs ![]() i and
i and ![]() i of Ώi and ΐi , respectively, the OLS residual is
i of Ώi and ΐi , respectively, the OLS residual is
y51 Εz
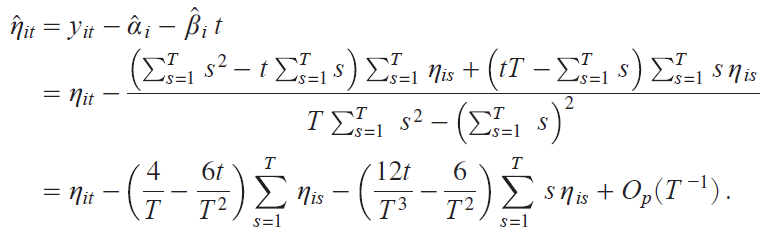
The continuous mapping theoremiCMTj yields, as T ¨ with N fixed,
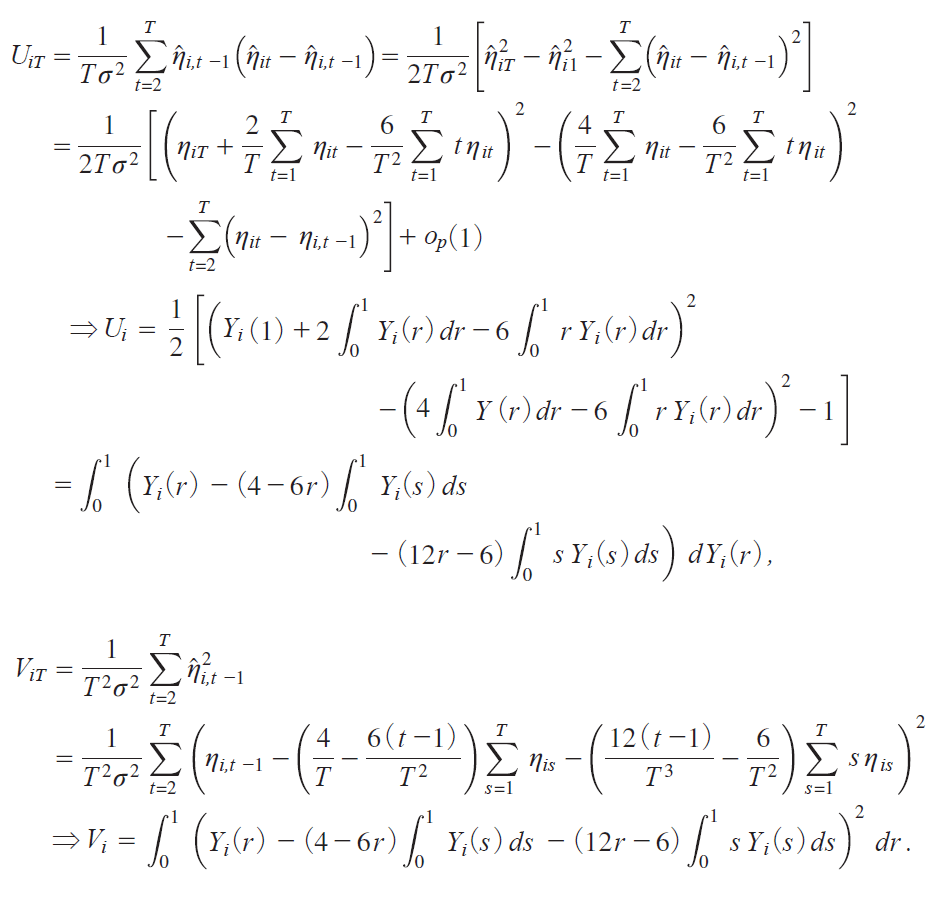
Thus the relationi12j is proved for Model D by the CMT.
@@We next deal with Model B, for which the OLSEs ![]() and
and ![]() of Ώ and ΐ are given by
of Ώ and ΐ are given by
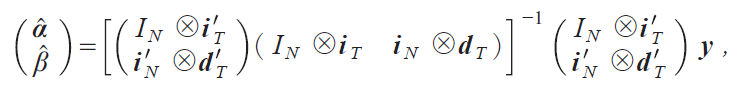
where IN is the identity matrix of order N, ⊗ is the Kronecker product, and
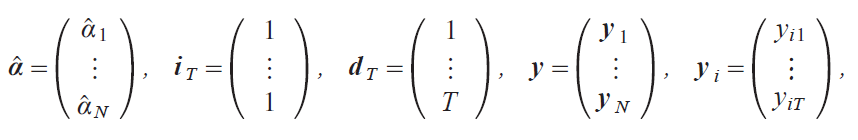
y52 Εz
We then have
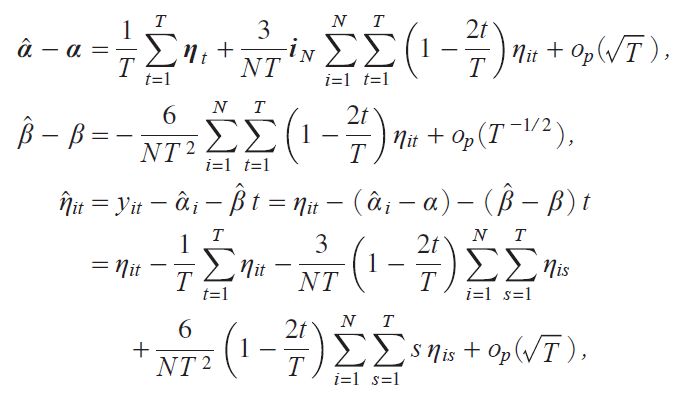
where ΕtiΕ1t , . . . , ΕNt j'. It follows that T i![]() iB j|1j
iB j|1j![]() UitiB j/
UitiB j/![]() VitiB j, where it holds that, as T ¨ with N fixed,
VitiB j, where it holds that, as T ¨ with N fixed,
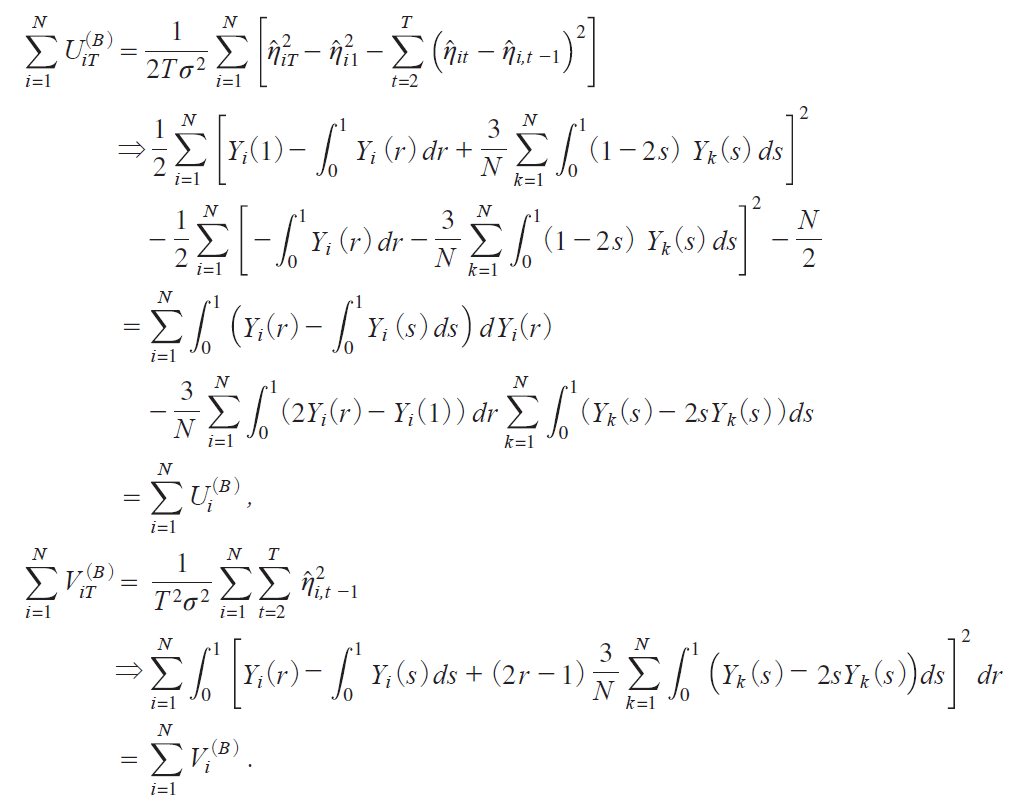
Let us put Y irjiY1irj, . . . , YN irjj'. Following Nabeya i2000j, consider Z irjHY irj, where H is the N ~N orthogonal matrix with the first row being i'N /![]() so that oZirjp
so that oZirjp![]() oYirjp and Y'irjiNY'irjH'HiN
oYirjp and Y'irjiNY'irjH'HiN ![]() Z1irj. Then it holds that
Z1irj. Then it holds that
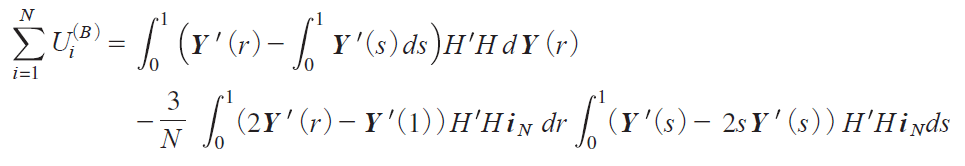
y53 Εz
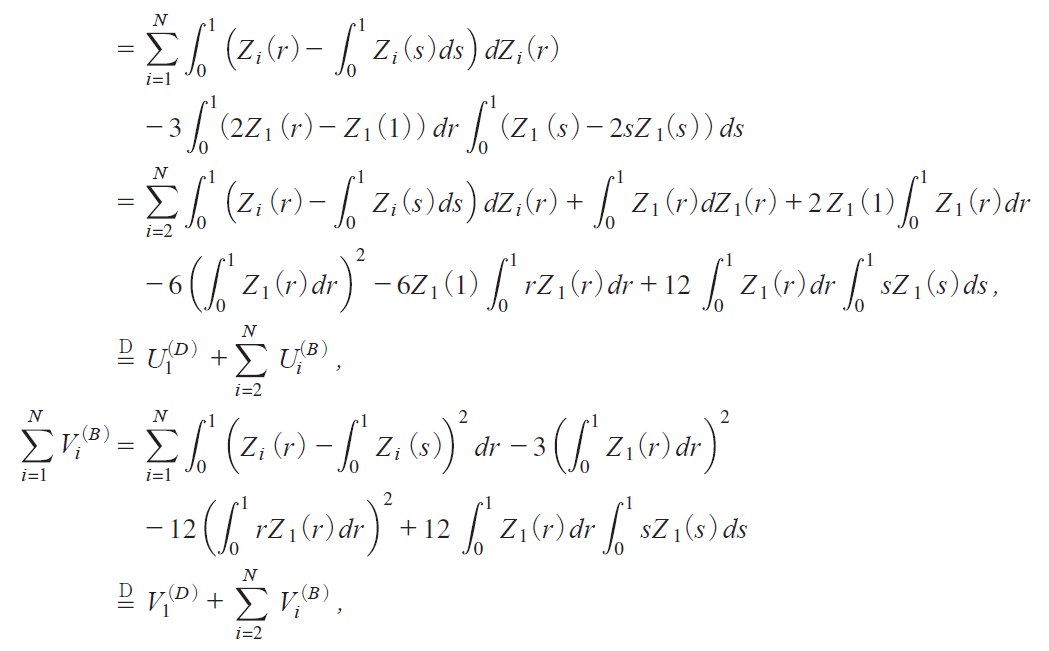
which shows thati12j holds for MB by the CMT. We can provei12j for MA and C similarly.
Proof of Theorem 2: Let us consider Model B. The joint m.g.f of Ui iB j and Vi iB j is given in the text, which can be used to compute first and second moments of these quantities as cN ¨ 0 by employing computerized algebra and the Taylor expansion. Here we show how to compute EiUi iB jj and VariUi iB jj. It follows fromi13j that
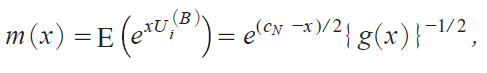
where
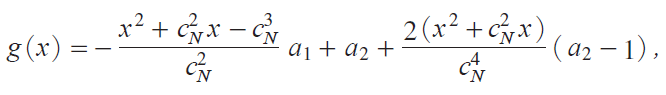
with gi0jecN , a1isinhcNj/cN and a2coshcN. Then we have
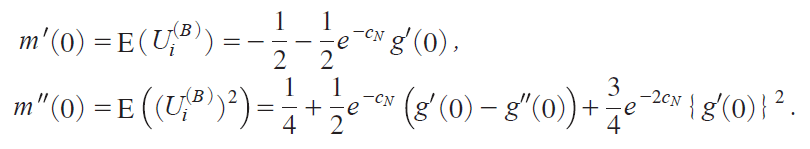
Here it holds that
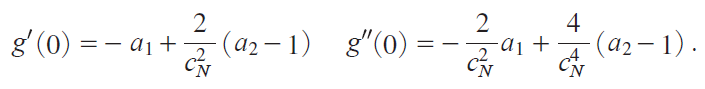
Then, using the expansions for e-cN , e-2cN , a1, and a2 as cN ¨ 0,
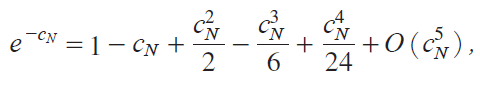
y54 Εz
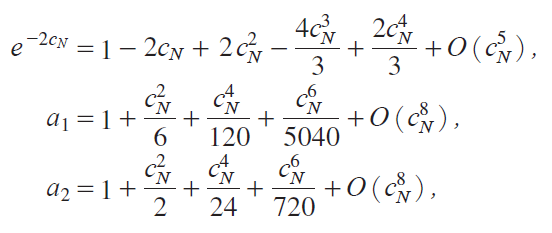
we can obtain moments of Ui iB j. We now have
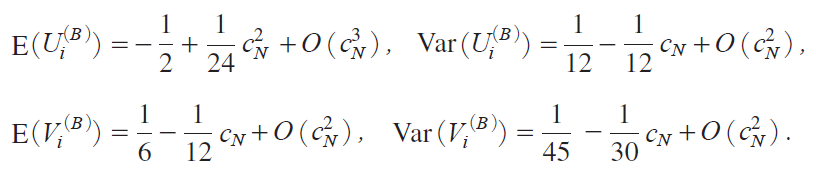
It follows from the WLLN that QNiB j ¨ |3 in probability. Thus we consider
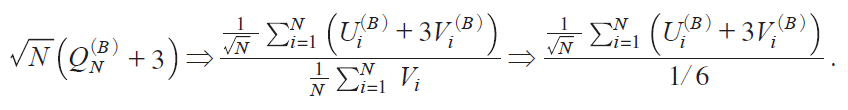
The m.g.f. of Ui iB j{3Vi iB j can be obtained from miB jix, y j by putting y3x, which yields
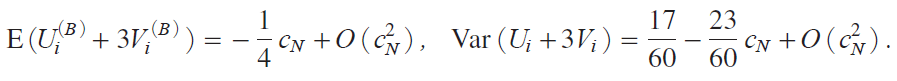
Putting cNc/![]() , we now have
, we now have
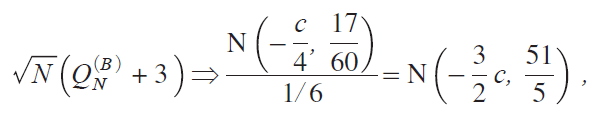
which proves the second relation in the theorem. We note in passing that
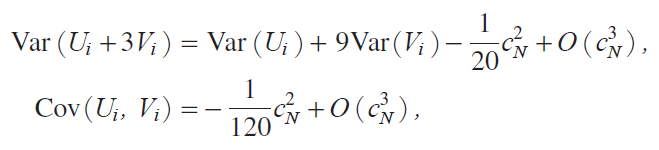
so that it holds that
are uncorrelated.
@@For the other models the first two moments of Ui iM j and Vi iM j as cN ¨ 0 can be obtained from their joint m.g.f.s given in Tanakai2017, Chap. 10j. More specifically we have
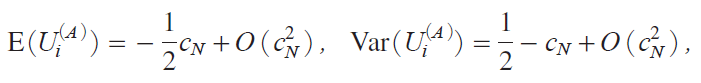
y55 Εz
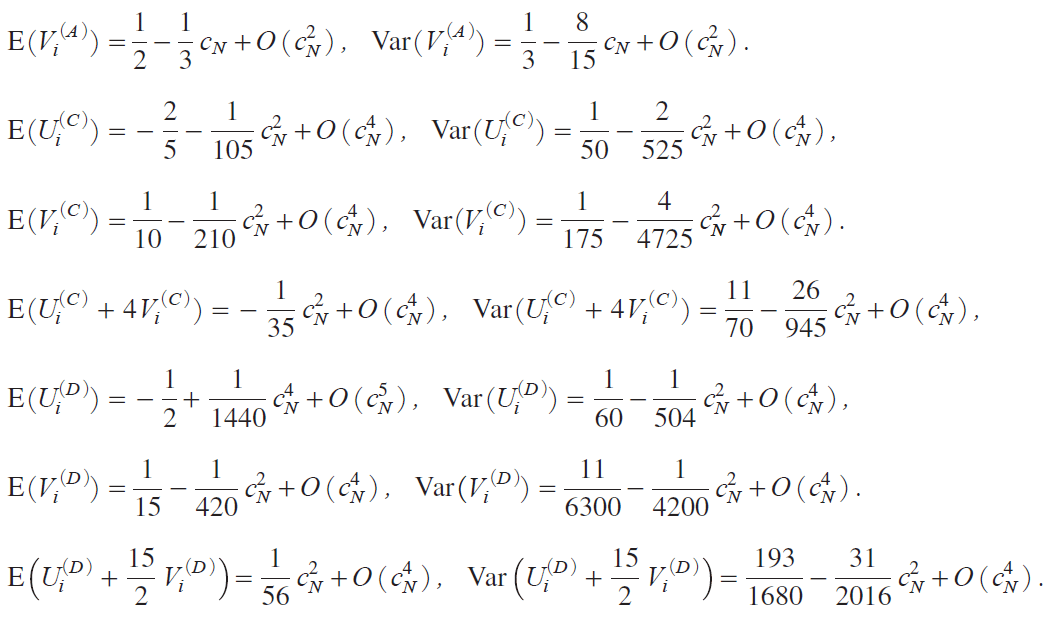
These moments yield the limiting powers for MA, C, D shown in the theorem, which establishes Theorem 2. We note in passing that, when cN0,
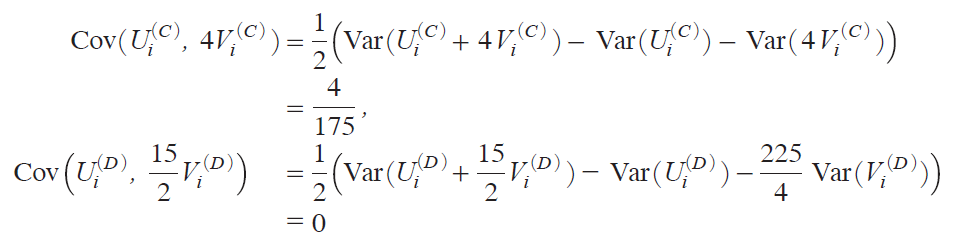
so that Ui iC j and Vi iC j are correlated, whereas Ui iD j and Vi iD j are uncorrelated.
Proof of Theorem 3: We first deal with Model D. Defining the T ~T lower triangular matrix C with C is, t j1 for s ≥ t and C is, t j0 for s t, the GLSEs of Ώi and ΐi are given by
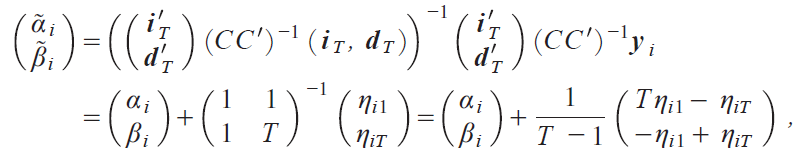
so that we have
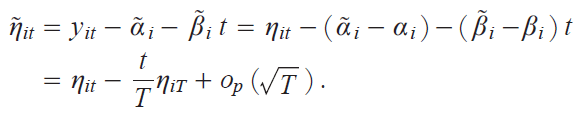
Consider T i![]() |1j
|1j ![]() Uit iD j/
Uit iD j/![]() Vit iD j. It holds that, as T ¨ with N fixed,
Vit iD j. It holds that, as T ¨ with N fixed,
y56 Εz
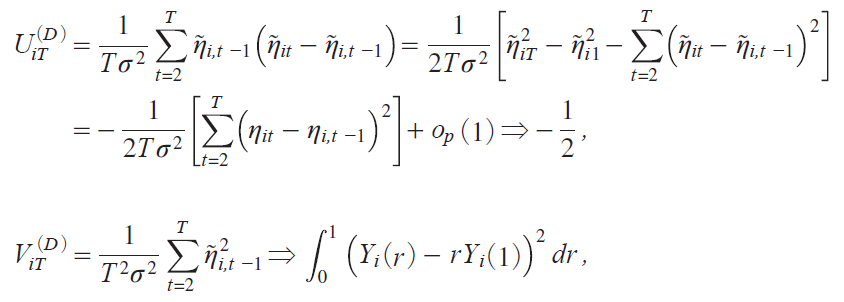
which provesi16j for MD.
@@We next consider Model B. The GLSEs of Ώ =iΏ1, . . . , ΏN j' and ΐ are given by
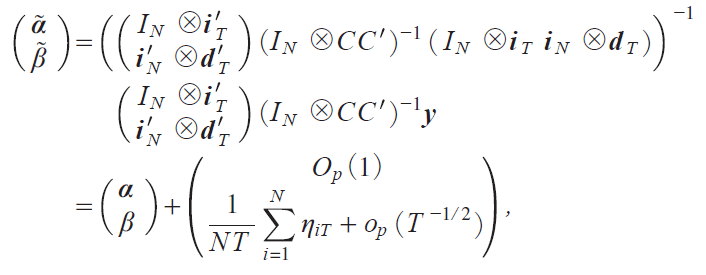
which yields
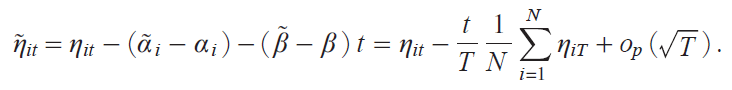
Then, applying the orthogonal transformation ZirjHYirj used in the proof of Theorem 1, it holds that, as T ¨ with N fixed,
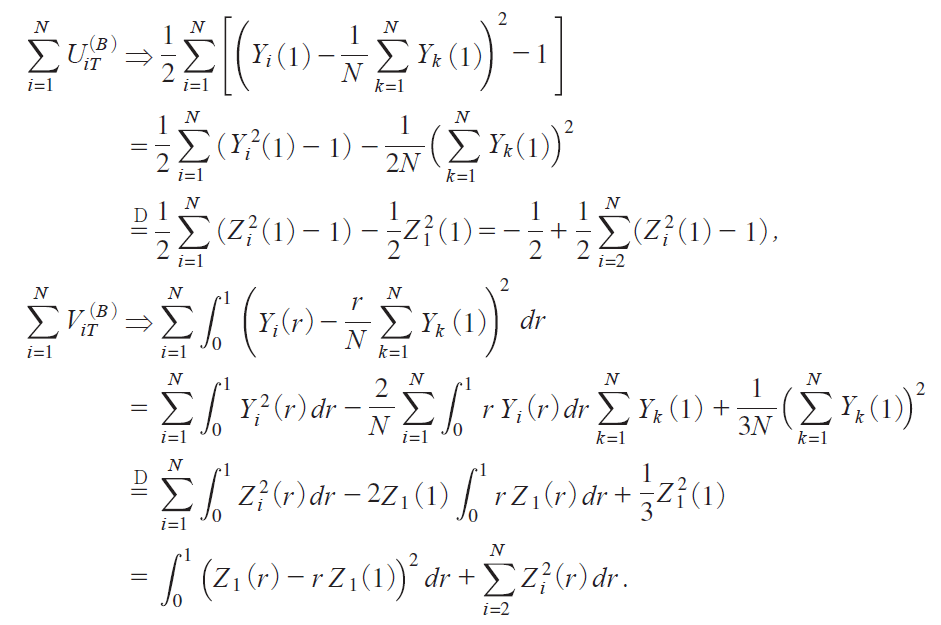
Noting thatoZ irjp![]() oY irjp, the relationi16j is proved for MB. We can provei16j for MA and C similarly, which establishes Theorem 3.
oY irjp, the relationi16j is proved for MB. We can provei16j for MA and C similarly, which establishes Theorem 3.
y57 Εz
Proof of Theorem 4: It follows from Theorem 3 that, as N becomes large,
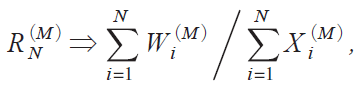
where Wi iM j and Xi iM j are defined in i16j. The limiting distribution of RNiM j for MA, B is the same as that of QNiA j in i12j, which proves the first relation. For Models C and D, Wi iM j|1/2, whereas the m.g.f. of Xi iM j is given in Tanakai2017, Chap. 10j and
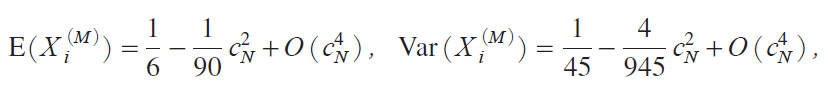
which yields RNiM j ¨|3 in probability. Then we consider
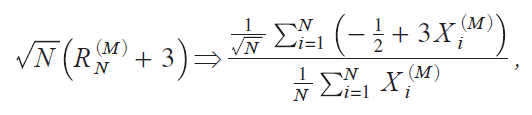
where
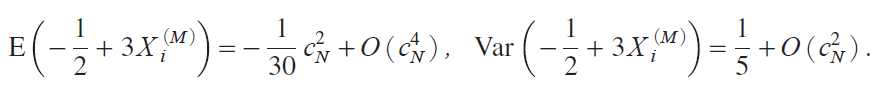
Putting cNc/N 1/4, we now have
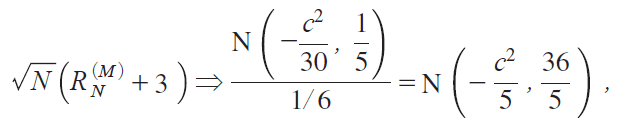
which proves the second relation, and Theorem 4 has been established.
Proof of Theorem 5: The relationi19j for Model D was proved in Tanakai2017, Chap. 10j. Let us consider Model B, for which it holds that
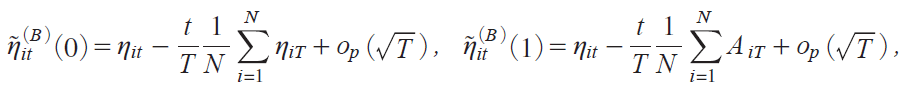
where
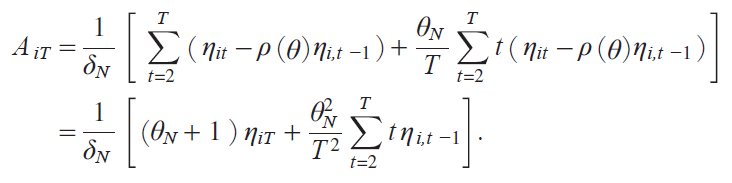
It holds that
y58 Εz
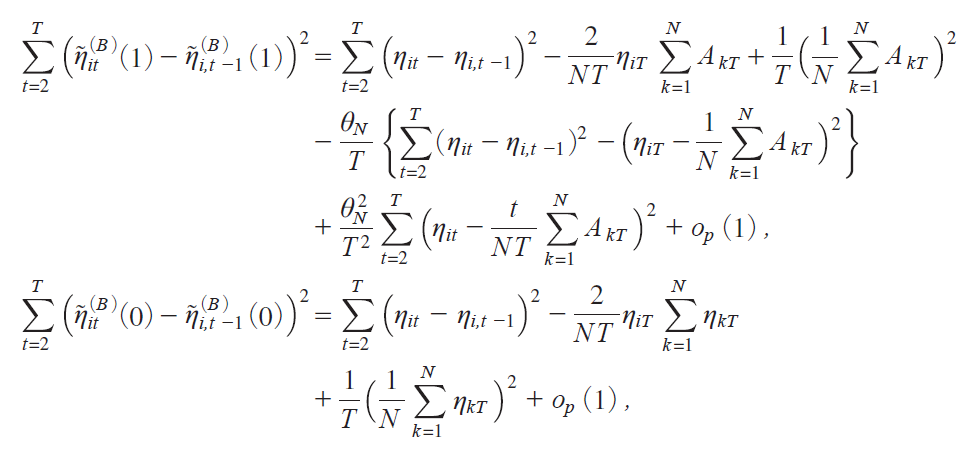
which gives
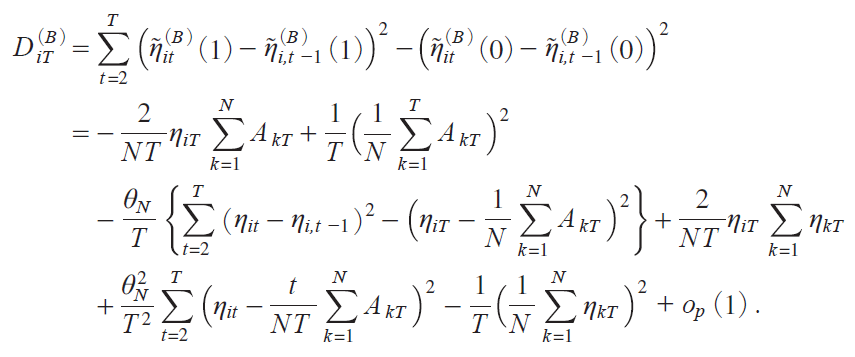
Thus it holds that, as T ¨ with N fixed,
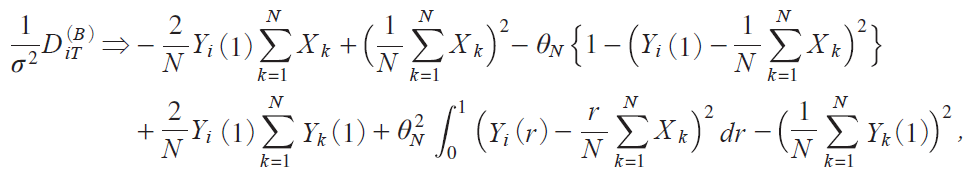
where
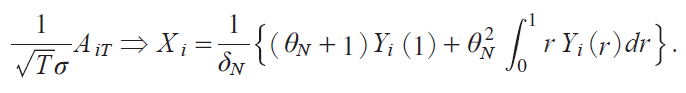
Applying the orthogonal transformation ZirjHYirj, we obtain
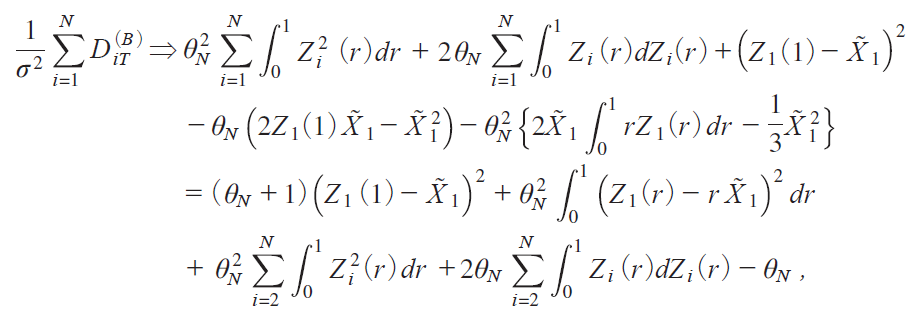
where
y59 Εz
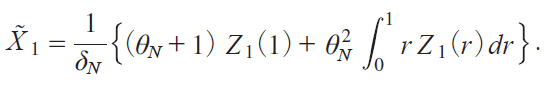
Noting that oZ irjp![]() oY irjp and
oY irjp and ![]() i
i![]() itiB ji0j|
itiB ji0j|![]() i,t|1iB ji0jj2/T ¨ Π2 in probability, we prove i19j for MB after some manipulations. We can prove i19j for MA and C similarly, which establishes Theorem 5.
i,t|1iB ji0jj2/T ¨ Π2 in probability, we prove i19j for MB after some manipulations. We can prove i19j for MA and C similarly, which establishes Theorem 5.
Proof of Theorem 6: For Models A and B we have SNiA jiΖj ![]() Zi iA jiΖj/N{opi1j, where Zi iA jiΖjis defined in i19j and the m.g.f. of iZi iA jiΖj{ΖN j/Ζ2N is given in Tanakai2017, Chap. 10j as
Zi iA jiΖj/N{opi1j, where Zi iA jiΖjis defined in i19j and the m.g.f. of iZi iA jiΖj{ΖN j/Ζ2N is given in Tanakai2017, Chap. 10j as
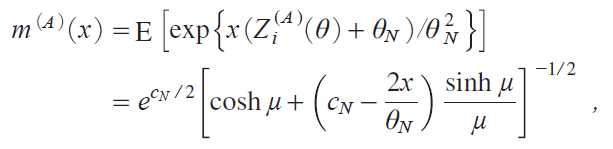
where Κ ![]() Differentiation of miA jixj gives us
Differentiation of miA jixj gives us
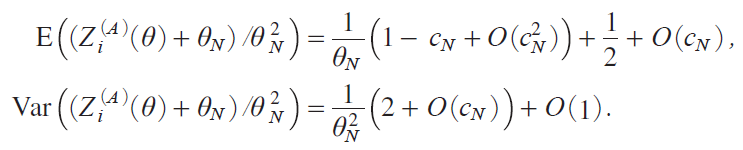
It follows from the CLT that, as N ¨ under ΖN = Ζ/N 1/2 and cN = c/N 1/2,
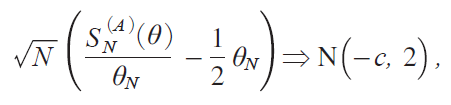
which yieldsi20j.
@@For Models C and D we have SNiC jiΖj![]() Zi iC jiΖj/N{opi1j, where Zi iC jiΖj is defined ini19j and the m.g.f. of iZi iC jiΖj{ΖN j/Ζ2N is given in Tanakai2017, Chap. 10j as
Zi iC jiΖj/N{opi1j, where Zi iC jiΖj is defined ini19j and the m.g.f. of iZi iC jiΖj{ΖN j/Ζ2N is given in Tanakai2017, Chap. 10j as
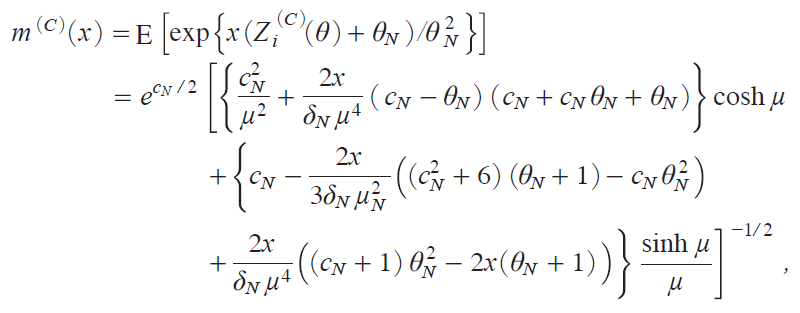
where Κ ![]() . Differentiation of miC jixj gives us
. Differentiation of miC jixj gives us
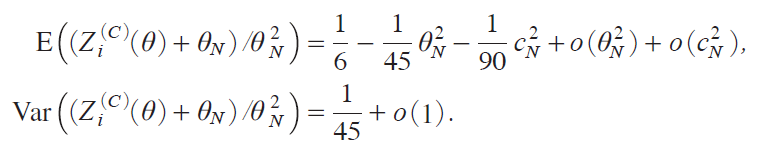
It follows from the CLT that, as N ¨ under ΖN =Ζ/N 1/4 and cN =c/N 1/4,
y60 Εz
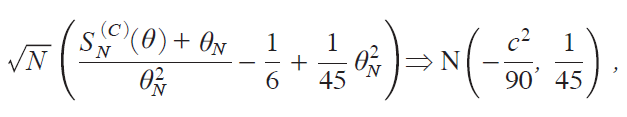
which provesi21j, and Theorem 6 has been established.
REFERENCES
Breitung, J. i2000j. The local power of some unit root tests for panel data. Advances in Econometrics 15:161-178.
Elliott, G., T. Rothenberg, and J. Stock i1996j. Efficient tests for an autoregressive unit root. Econometrica 64:813-836.
Imhof, J.P. i1961j. Computing the distribution of quadratic forms in normal variables. Biometrika 48:419-426.
King, M.L. i1987j. Towards a theory of point optimal testing. Econometric Reviews 6:169-218.
Moon, H.R. and B. Perron i2008j. Asymptotic local power of pooled t-ratio tests for unit roots in panels with fixed effects. Econometrics Journal 11:80-104.
Moon, H.R., B. Perron, and P.C.B. Phillips i2007j. Incidental trends and the power of panel unit root tests. Journal of Econometrics 141:416-459.
Nabeya, S. i2000j. Asymptotic distributions for unit root test statistics in nearly integrated seasonal autoregressive models. Econometric Theory 16:200-230.
Nabeya, S. and K. Tanaka i1990j. A general approach to the limiting distribution for estimators in time series regression with nonstable autoregressive errors. Econometrica 58:145-163.
Tanaka, K.i1996j. Time Series Analysis: Nonstationary and Noninvertible Distribution Theory. New York: John Wiley & Sons.
Tanaka, K. i2017j. Time Series Analysis: Nonstationary and Noninvertible Distribution Theory. 2nd ed. New York: John Wiley & Sons.
Tanaka, K. i2018j. Computing limiting local powers and power envelopes of panel MA unit root tests and stationarity tests. to appear in Econometric Theory.