�y281�Łz
���w�pWeb���ގ��������̂��߂�
���ޓ��e�̈Ӗ��Ɋւ���XML�^�O��`
���c�@�R���� ��
�@
�{�e�ł́C�}�N���o�ϊw�ɂ����ďd�v�ȍ����������胂�f�����������Web���ނ�����Ƃ��āC��X�̊J������e-Math Interaction Agent�Ƃ������w�pWeb���ގ��������V�X�e�����Љ��B�{�V�X�e���͐l�Ԃɑ�����XML�t�@�C�������邪�C�{�_���ł́C���w�p�}���`���f�B�A���ޒ�`�ɂ��ĕK�v�ƂȂ�XML�^�O���C���C�A�E�g��`�p�Ɩ��̈Ӗ���`�p��2��ޕK�v�ł��邱�Ƃ�������C��������������ɂ����Ē�`�����Ӗ��IXML�^�O���������B�����������̈Ӗ��I�^�O��`�͉��z���t�̃K�C�_���X���C����̐����y�ѕϐ��Ԃ̊W�����t�C2�������邢��3�����̃O���t�ȂNJe��̕\�����@�Ő�������ꍇ�ɕK�{�ł���B
�@
XML Tag Definition for Expressing Semantics of Mathematical Contents in Web-Based Courseware Automation
Yukari SHIROTA ��
In the paper, Web-based learning materials for a national income determination problem in macroeconomics are presented as sample materials for explanation of our developed mathematical courseware automation system named e-Math Interaction Agent. This system automatically generates target XML files instead of human programmers. In the paper, it is described that there are two kinds of XML tags should be defined for the automation. One is defined for a Web page layout and another is for definition of semantics in the given mathematical problem. This semantic definition is required for generation of higher qualitative virtual teacher's guidance so that the teacher can explain semantics of an equation or a relationship between two variables in various expressions such as words, 2 or 3 dimensional graphs.
�@
�y282�Łz
1�D�͂��߂�
��X�͐��w�pWeb���ނ̎��������V�X�e���ɂ��Č������Ă���C���̎���Ƃ��Đ��w�œK��������������Web���ނ̎��������V�X�e��"e-Math Interaction Agent"���J�����C��N�x����w���Ɏ��K�p�Ƃ��Č��J���Ă���B�{e-Math Interaction Agent�V�X�e���̓����́C�������ꂽ���ނ��w�������s����Ɖ��z�L�����N�^���t����ʏ�ɏo�����Đ������ĕ������Ă���邱�ƁC���̉��z�L�����N�^�ɂ���b�@�\���\��XSLT��Ƀv���O���~���O���Ă��邱�ƁC�y�сC���w�̌�����o�ς̊T�O�E�m���Ȃǂ�\�ߒm���x�[�X�Ɋi�[���C���̌�����g�ݍ��킹�邱�ƂŃS�[���ł���W�������邱�ƁC�y�сC���������V�X�e���ɂ��MathML��C���[�W�t�@�C���Ȃǂ�Web��̐����\�����v�Z���C������������@�\�������������Ƃ���������B�����̋@�\�ɂ��C���t�͐��w�ׂ̍����v�Z�y�т��̐����\����Web���ɔ����ώG�ȍ�Ƃ���������C����ɁC�R���s���[�^�m�����Ȃ����t�ł����z�L�����N�^��p�����w���Ƃ̉�b�@�\�������w���ނ����������\�ƂȂ���1,2�B
���̃V�X�e���̌��ƂȂ鋳�ގ����������f���́C���w�̌�����S�ʂɓK���\�Ȕėp���f���ł���C���p�͈͂��L���B�e��̐��w���̉�@�v�������`���邱�Ƃɂ��C���̃^�C�v�̐��w�����������鋳�ނ������������邱�Ƃ��\�ƂȂ�B����������ׂ�����C�Ώۖ��Ƃ��Čo�ςɂ����鍑�������������グ���B
����̎����ɂ�����O��̊g���@�ł��邪�C�����I�Ȃ��̂Ƃ��ẮC���������V�X�e��Maple�̃X�N���v�gMaplet�ɂ��O���t�������\�Ƃ����_����������B����ɂ��w���̓O���t�̃p�����[�^���ʂɁC���Θb�I�ɕς��邱�Ƃ��\�ƂȂ����B�O�o�[�W�����ł̓O���t�͐Î~��̕\���݂̂ł������B�{�w�ł�2004�N�t����L�����p�X���̑S�R���s���[�^���Maple���ғ��\�Ƃ������߁C�N���C�A���gPC��Ōʂɐ��������y�уO���t�`����s����C���̂悤�ȃV�X�e���\�����\�ƂȂ����B�܂��_���I�Ȋg���Ƃ��ẮC���w���̈Ӗ��Ɋւ���^�O��`��XML�^�O��`�ɂ����čs�Ȃ����_�ł���B�{�e�ł́C���̐��w���̈Ӗ��Ɋւ��郁�^�f�[�^���������B
���߂ł́C��X����Ă��鐔�w�p���ނ̎��������Ɋւ���ėp���f�����������B�����Ă�����ǂ̂悤�Ɏ������邩�C�ėp�̃V�X�e���\�����q�ׂ�B��3�߂ł́C��X����`������������������p���ނ̉�@�v���Z�X�d�l�ɂ��ďq�ׂ�B��4�߂ł́C���������}���`���f�B�A���ޒ�`�ɂ��ĕK�v�ƂȂ�XML�^�O���C���C�A�E�g��`�p�Ɩ��̈Ӗ���`�p��2��ޕK�v�ł��邱�Ƃ�������C��������������ł͂ǂ̂悤�ɈӖ��IXML�^�O���`���������������B�ŏI�͂͂܂Ƃ߂Ƃ���B
2�De-Math Interaction Agent�̃V�X�e�����f���y�уV�X�e���\��
�{�߂ł͉�X����Ă��鐔�w�p���ނ̎��������Ɋւ���ėp���f�����������B�܂��C������ǂ̂悤�Ɏ������邩�ėp�̃V�X�e���\�����q�ׂ�B
���w���ɂ́C������Əؖ�����2��ނ����邪�C��X�̊J������V�X�e��e-Math Interaction Agent���ΏۂƂ�����͌�����S�ʂł���B������Ƃ́C���m�������߂邽�߁C�܂��A���������𗧂ĂāC�����Ă���������Ƃ����`���̖��ł���B�o�ϐ��w���܂ޏ������y283�Łz�w�ɂ����Ă͏ؖ�������������̂ق����p�o���Ă���C�w���ɂƂ��Ă܂������肪�m���ɉ����邱�Ƃ��d�v�ƌ�����B�܂����w��苳�ގ��������̎����\������l�����ꍇ���C�ؖ����ɔ�r���Č�����̕������̎����\���������ƍl�����D����ĉ�X�͂܂��C�����肩�璅�肷��B�ؖ����������������邽�߂ɂ́C���������V�X�e�������ł͕s�\���ł���CProlog�x�[�X�̎����ؖ��V�X�e�����K�v�ƂȂ�B���Ƃ��CMelis�̃O���[�v�ł͎����ؖ��V�X�e����MEGA3��p���ďؖ������������鋳�ނ̎��������̌������s���Ă���4�B
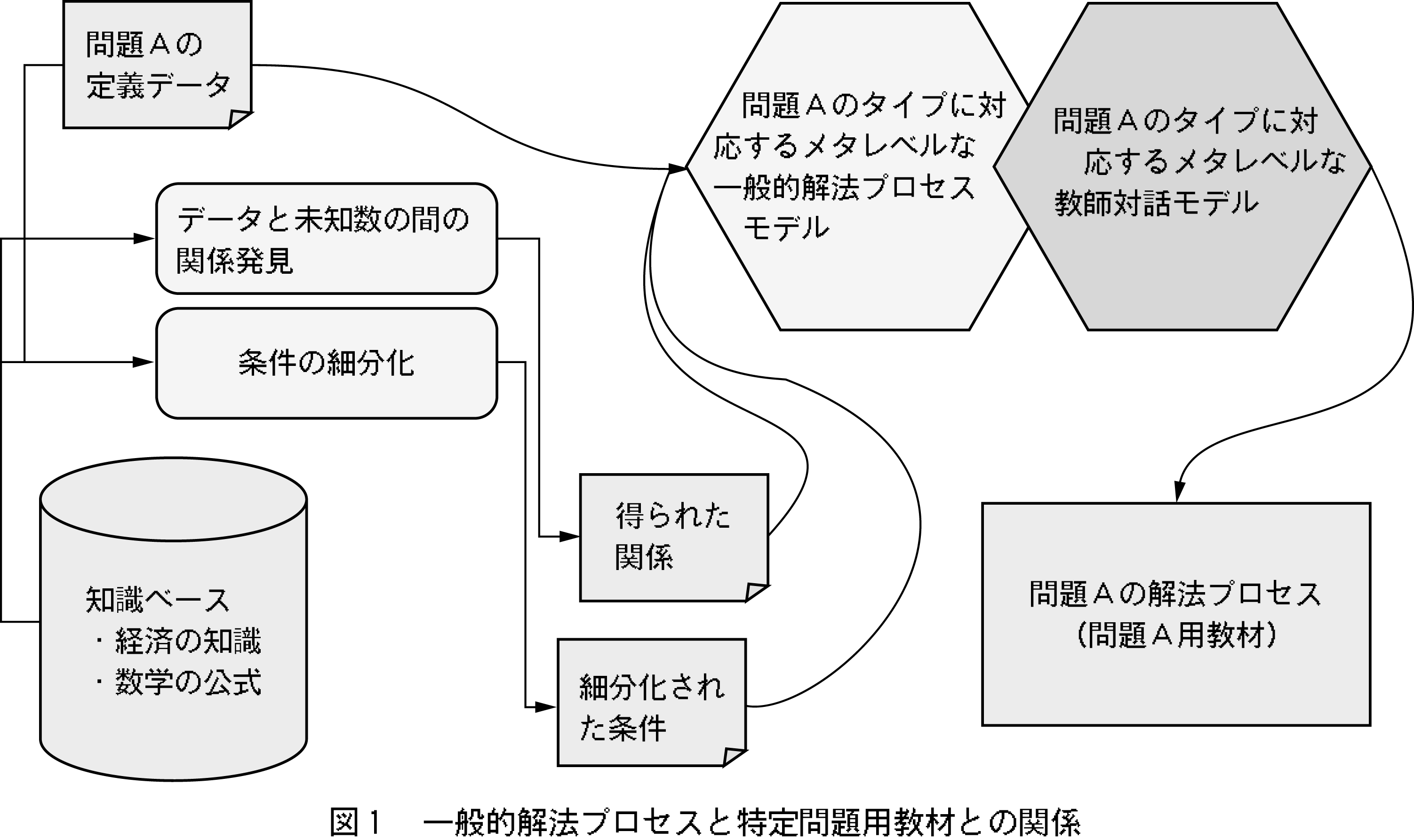
���߂ɉ�X�̒�Ă��鐔�w���ސ�����@�̃��f�����������i�}1�Q�Ɓj�B�܂��C�������鐔�w���������@�v���Z�X�ɂ�蕪�ނ���B�܂��@�v���Z�X������̃X�L�[�}�������̏W�������B�Ⴆ�C�u1�Ɨ��ϐ��̍œK�����v�C�u���ϐ��̍œK�����v�C�u���O�����W�F�̖���搔�@�v�ȂǂƂ��������̏W�������B�����@�v���Z�X�ʼn�������́C���̃^�C�v���������ƌĂԁB�����āC�\�߂��ꂼ��̖��^�C�v���ƂɑΉ������@�v���Z�X���f�����쐬���Ă����B�}1�ł͂�����u���`�̃^�C�v�ɑΉ����郁�^���x���Ȉ�ʓI��@�v���Z�X���f���v�ƋL�ڂ��Ă���B����͐��w��@�A���S���Y���ɑ�������B��ʓI��@�v���Z�X���f���쐬���s���l���V�X�e���E�X�[�p�[�o�C�U�[�ƌĂԁB�V�X�e���E�X�[�p�[�o�C�U�[�Ƃ́C���w���t�ł���C���R���s���[�^�Z�p�ɐ��ʂ����G�L�X�p�[�g�ł���B�V�X�e���E�X�[�p�[�o�C�U�[�̓��^���x���Ŗ��^�C�v�ɋ��ʂȐ��w��@�v���Z�X�C�y�сC�w���ւ̐��w��苳���@���`����\�͂������Ȃ��Ă͂Ȃ�Ȃ��B
�@

�@
����Ɋw���ւ̋����@�ɂ����āC�ǂ̂悤�Ɋw���ɋ������邩�Ƃ����v���[���e�[�V�����w�ɑ������郂�f�����K�v�ƂȂ�BInteraction Agent�V�X�e���ɂ����Ă͉��z�L�����N�^���t�ɂ��Θb���d�����Ă���̂ŁC���^�C�v���Ƃɉ��z���t�Ƃ̑Θb�e���v���[�g���쐬���Ă����B���ꂪ�}1�ɂ���u���A�̃^�C�v�ɑΉ����郁�^���x���ȋ��t�Θb���f���v�ł���B�V�X�e���E�X�[�p�[�o�C�U�[�͗\�߃��^���x���őΘb�e���v���[�g���`���Ă����B�����ċ��ސ������܂�C�X�̐��w���̒�`��V�X�e���ɓ��͂��ꂽ���_�ŁC�V�X�e���͂��̖����y284�Łz�L�̏������̃e���v���[�g�ɖ��ߍ��ނ��Ƃɂ���āC�ŏI�I�ȑΘb��������������B
�}1�Ɏ�����ʓI��@�v���Z�X���f���C�y�сC���t�Θb���f�����C�����^�C�v�̖��S�̂ɋ��ʂ��郁�^���x���ȃ��f���ł���B�����ɁC���������ŗL�̖���`������͂��邱�ƂŁC���̖��ŗL�̋�̓I������K�p������@�v���Z�X�C�y�сC���̖����w���ɋ������邽�߂̋��ނ������������邱�Ƃ��\�ƂȂ�B�d�v�Ȃ��Ƃ̓V�X�e���E�X�[�p�[�o�C�U�[���u�ǂ̂悤�ɂ��̐��w�����w���ɋ�������C������ʂ��������v�ƍl���ʂ����Ƃł���B���̃��f���쐬�Ɏ��Ԃ������邱�Ƃɂ��C����ȍ~�C���ꃁ�^���f�������ʂɎ������������e�푽�l�Ȑ��w���ނ̎��̌��オ�}���B���w���t�����̋����@�ɂ��Ċe�l�̃m�E�n�E�����悤�ɁC���w���^�C�v�̕��ދy�т��̉�@�v���Z�X���f���̒�`�̓V�X�e���E�X�[�p�[�o�C�U�[�X�l�Ɉˑ�������̂ł���C�V�X�e���E�X�[�p�[�o�C�U�[���قȂ�ΈقȂ��@�v���Z�X���f������`�����B
Interaction Agent�V�X�e���ł̓V�X�e���E�X�[�p�[�o�C�U�[���\�߁C��@�v���Z�X���f���y�ы����@���f����Perl�Ńv���O�������Ă����B����Perl�v���O�������l�Ԃ̃v���O���}�ɑ�����XML�t�@�C���������o���B�܂�������XML���p����XSLT�X�^�C���V�[�g���Ŏg����XML�^�O�̒�`�C�y�сC�X�^�C���V�[�gXSLT���̂̍쐬���V�X�e���E�X�[�p�[�o�C�U�[�̎d���ł���B
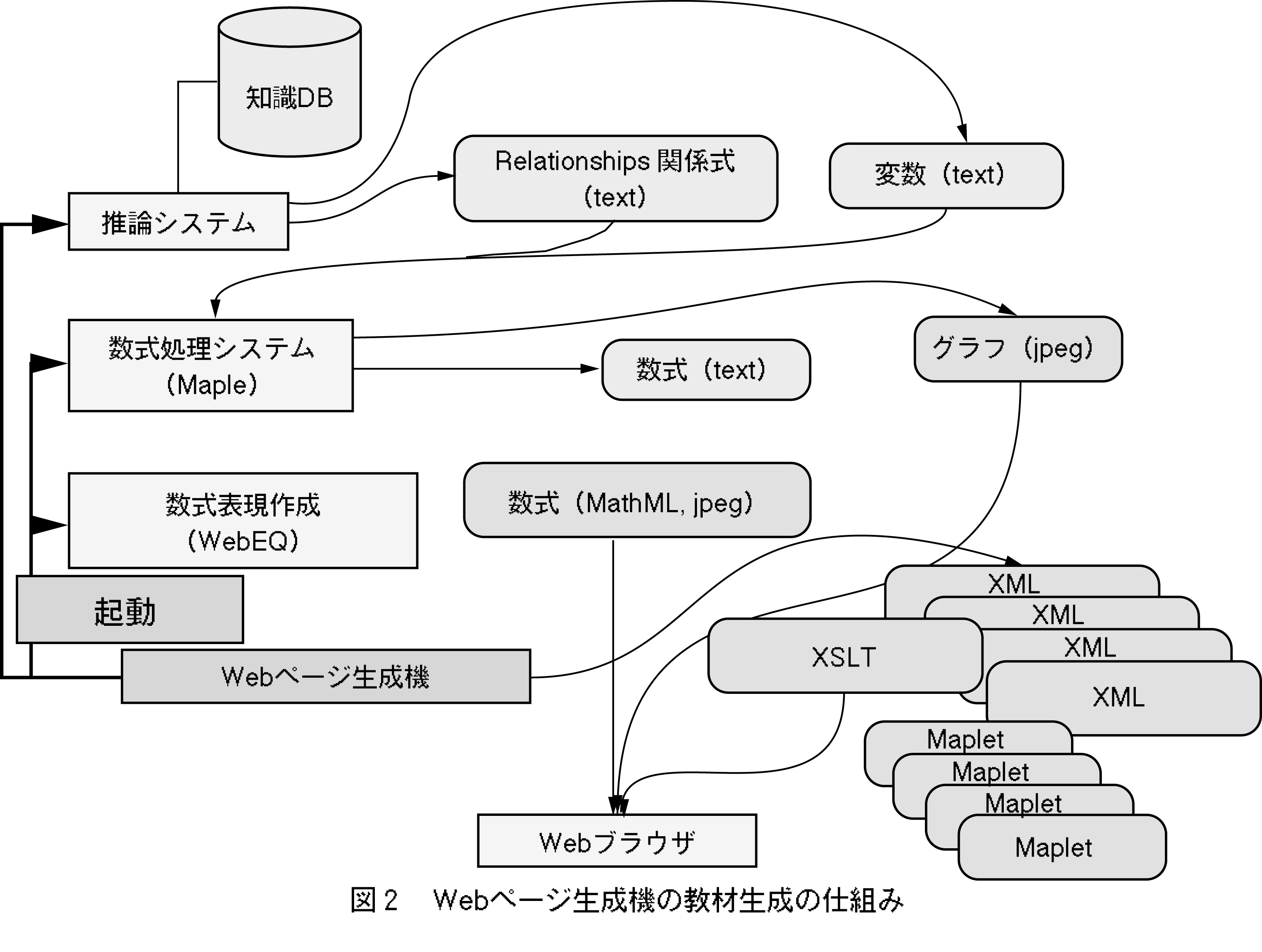
�����L�̖���`�������^���x���L�q�t�@�C���ƌĂԁB���^���x���L�q�t�@�C���̗�͎��߂Ŏ����B�{Interaction Agent�V�X�e���́C���̃��^���x���L�q�t�@�C���̓��݂͂̂����ɂ��C�Ή�����XML�t�@�C����������������B���̍ۂ�,���C���v���Z�X�ƂȂ�Web�y�[�W�����@����C�ȉ���3�̃T�u���W���[�����K�v�ɉ����ČĂяo�����i�}2�Q�Ɓj�B
�@
�@
�y285�Łz
�i1�j���_�G���W���iProlog�C���^�v���^�j�B
�i2�j���������V�X�e���iMaple5�j�B
�i3�j�����\���쐬�V�X�e���iEquation Server, WebEQ6�j�B
���������V�X�e���͐l�Ԃɑ����ė^����ꂽ�A������������ϕ��Ȃǂ̖����L���I�ɉ����B�܂��K�v�ɉ����ē��I�ɃO���t��`�悷�邽�߁C���������V�X�e���̃O���t�`��@�\��p���Ă���B��X�̑�w�ł͑S�Ẵp�\�R����Ő��������V�X�e��Maple�����p�\�ł���C�{�V�X�e����Maple�𗘗p���Ă���B�œK����苳�ނ��쐬����O�o�[�W��������CMaple�Ɋւ��Ĉȉ��̊g�����s�����B
�i1�jOpenMaple API�Ƃ��Ăb����p�C���^�t�F�[�X���V�������[�J�[������ꂽ�̂�Maple�̃A�N�Z�X�����ׂĂ���API���g���ď����������B����ɂ��啝�Ƀp�t�H�[�}���X�����サ���B
�i2�j�O���t�\���̍ہC����3�����O���t��Θb�I�Ɋw�����������Ċώ@���邱�Ƃ��ł���悤�ɂ��邽�߁CMaple�̃O���t�\���p�ȈՃX�N���v�g�ł���Maplet�i���[�v���b�g���邢�̓}�v���b�g�Ɠǂށj���̗p�����B�}2�̍\���}�ɂ�����悤�ɁCWeb�����@�͂���Maplet�t�@�C����K�v�ɉ����ď����o���BMaplet�̎��s�̗l�q�͎��߂Ŏ����B
Maplet��p���闘�_��2����B
�i1�j�w�����w�K���Θb�I��3�����O���t�������Ƃ��\�ƂȂ�B�����Maplet�t�@�C������w���̃��[�J���R���s���[�^��ɑ��݂���Maple�̃v���Z�X���N������邩��ł���B
�i2�jMaplet�̃R�[�h�͍��@�\�Ȃ̂ŏ����R�[�h�s�����Ȃ��Ă��ށB����ăO���t����p�X�N���v�g�̎��������������ȒP�������B
���ގ����������}2�Ɏ����悤�ɁC�A�����������������邽�߂ɐ��������V�X�e�����N������B���̌��ʂƂ��ăe�L�X�g�`���̐������Ԃ�B���̃e�L�X�g�`��������Web�ŕ\���\��MathML�y��jpeg�Ȃǂ̌`���ɕϊ�����̂��C�����\���쐬�V�X�e���ł���B�܂��CWeb�y�[�W�����@�ɂ�萶�����ꂽXML�ł́C�������ꂽ�����̐}�t�@�C���y��Maplet�t�@�C���Ȃǂ��t�@�C���Q�Ƃ���`�ł��̉�ʂɊ܂߂ĕ\������B�g�p����XSLT�́C�\�ߎg���������z�L�����N�^�̎�ނȂǂɂ��w�肵�Ă����B���݂�Interaction Agent�V�X�e���ł́C���z�L�����N�^�Ƃ���Microsoft Agent7�𗘗p���Ă���B����Microsoft Agent�̐����VBScript����ɂ����XSLT��Ƀv���O��������B
3�D����������������������鐔�w����
�{�߂ł͖��^�C�v�̎���Ƃ��āC������������������グ�āC���ދy�і{�V�X�e���̎d�l���������B��������������Ɋւ�������͌o�ϐ��w�̃e�L�X�g���Q�Ƃ��Ē�������8,9,10�B�}�N���o�ϊw�͍����������x���Ɋւ���o�ϊw�I���_�y�ѐ���Ɋւ���w��ł���C���̒��S���Ȃ���������������𗝉����邱�Ƃ͌o�ϊw���̊w���ɂƂ��ċɂ߂ďd�v�Ȃ��Ƃł���B�Ⴆ�C���ԓ�����{�̌������ƂȂǂɂ��x�o�ɂ���Ďx�o�S�̂����������ꍇ�C���ꂪ���������̑����ɂ����ɉe�����y�ڂ����ɂ��āC��������������͉���^���邪�C�y286�Łz�������I�ɗ������邾���ł͐[�����𗝉������Ƃ͌����Ȃ��B�����Ōo�ϓI�t�@�N�^�[�Ԃ̊W��A���������̏�Ő��w�I�ɂ����������邱�Ƃ������]�܂��B�܂����w�Ȃ̊w���ɂƂ��Ă��C�A���������̎��Љ�ł̉��p�Ƃ��āC�����B�̌o�ώЉ�̎d�g�݂𗝉����邱�Ƃ͔��ɈӋ`������B���ގ��������V�X�e���Ƃ��Ă̗��_�����_�ł��C��������������̋��ނ�������������Ӌ`�͑傫���B���R�́C�ݒ肷��o�σ��f���̈Ⴂ�ɂ�葽���̃o���G�[�V���������݂��邩��ł���B�܂����̃��f�����ɂ͑����̌o�ϕϐ������݂����G�Ȉˑ��W�����̂ŁC���f�����Ƃɂ��̘A���������ɂ�����t�@�N�^�[�Ԃ̊W�C�܂�u���̕ϐ������ƌ��ʂƂ��đ��̕ϐ����ǂ��ω����邩�v�Ƃ����W�𐔊w�I�ɐ��������������邱�Ƃ͈Ӌ`������B����ɁC��������������́C���̃V�t�g�������Љ�̌��ۂƌ��т��ċ������邽�߂̍œK�̋��ނƌ�����ł��낤�B
�{e-Math Interaction Agent�V�X�e���͘A��������������������S�ʂɓK���\�Ȃ̂ŁC�A�����������\�����Ă��镨�i�ϐ��j�ƕ��Ƃ̊Ԃ̊W�𗝉������邽�߂̊e��̐���������@�\�́C�o�ϖ�肾���Ɍ��肳�ꂸ�C�L���K�������B����č�������������Ő��������e�틳�ނ�������͂́C�����܂ł�����ł���B
�{�߂Ő������鐔�w���̃^�C�v���́u��������������v�Ƃ����B����͌o�ϊw�W�҂̊Ԃł͂��̕����C�����������̂ł����������C���w�I�Ɍ���Ɓu�ύt�l�ւ̉e�����͖��v�Ƃ��������K�ł���B��ʂɈȉ��̂悤�ɒ�`�ł���^�C�v�̖��ł���B
�u�A������������2�ϐ��`�y�тa�̊ԂɁC���̑��̓Ɨ��ϐ��w�����ύt�WA(X)=B(X)������ꍇ�C�ύt��Ԃ̂w�̒l���C���̕ϐ��̕ϓ��ɂ��ǂ̂悤�ȉe�����邩���߂�v
�o�ϊw�ɂ����Ă��̃^�C�v�̖��͕p�o���Ă���B�����͕č���GRE Economics�̖��ɂ������o�肳��Ă���11�B��������������ȊO�ł��C�Ⴆ�Ύ��v�Ƌ����̋ύt�W�Ɋւ��鑽��̖�肪����B����Ė{���Ɋւ��鎩�������͗L�p���������ƌ�����B
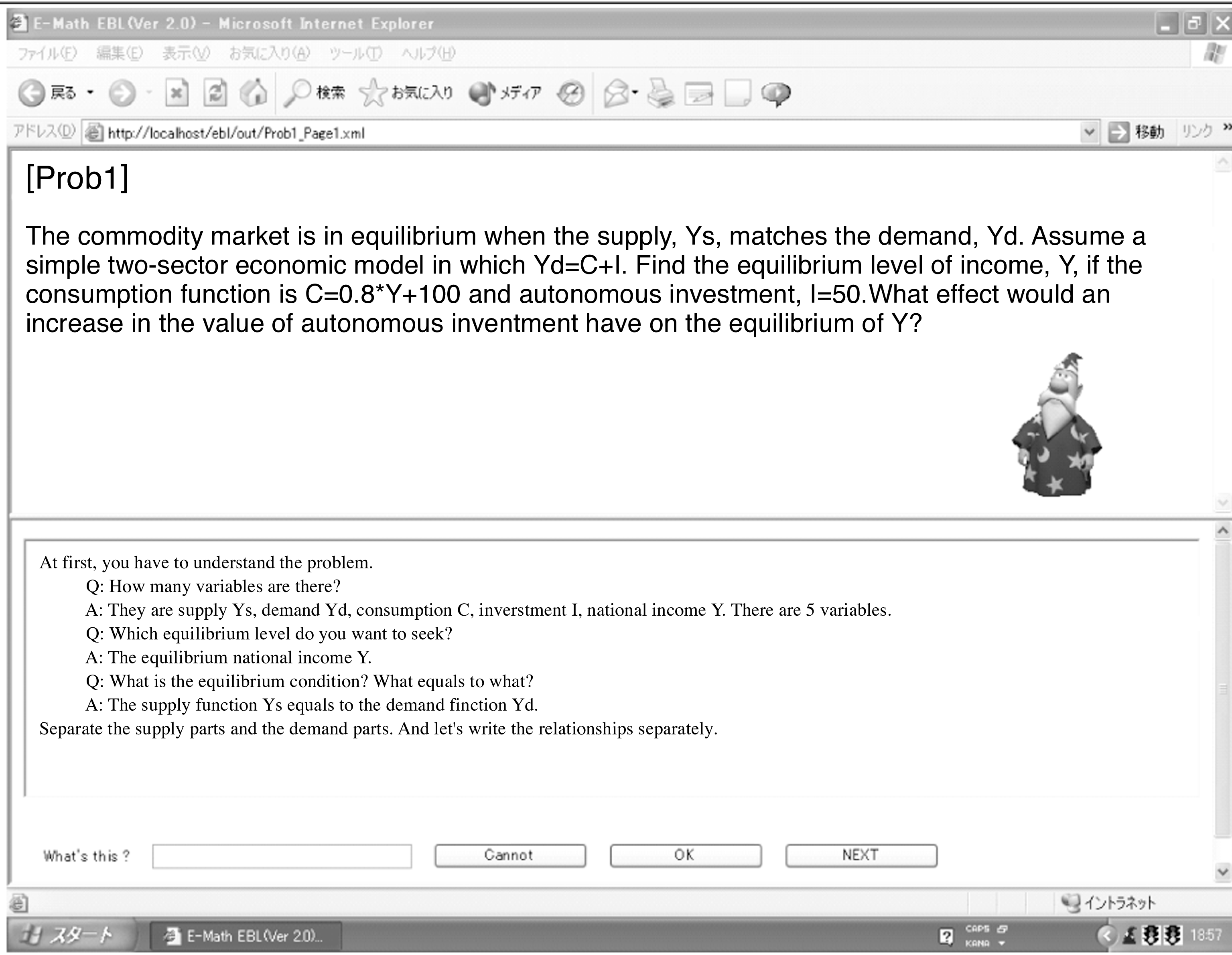
�{�߂ł́C��������������̗�Ƃ��āC�}3�Ɏ����������������ƂƂ���B���̖��ł́C������������ɂ����ē����iInvestment�j�̕ϓ��ɂ��ύt���������iY*�j�ւ̌��ʂ����₵�Ă���B�{Web���ނ́C�{�w�̃L�����o�X�l�b�g���[�N���ɂ����Ċw���̎��K�p�Ɍ��J����Ă��邪�C�V�X�e���\���Z�p��̖��C���̑��̗��R���狳�ނł͉p����g���Ă���B
�@
�@
�n�߂ɒ���镶�͑�̕��͂ł��邪�C����̓t���[�t�H�[�}�b�g�ŋ��t���앶��������w���ɕ�����Ղ��̂ŁC���͑蕶�͂͐l�ԋ��t���������̃t�@�C�����V�X�e���ɗ^���邱�ƂƂ����B
�V�X�e���E�X�[�p�[�o�C�U�[�Ƃ��ĉ�X�́u��������������v1��ɑ��C6�X�e�b�v�C�܂�6�y�[�W����Ȃ�Web���ނ��쐬���邱�ƂƂ����B�ȉ����ɃX�e�b�v��ǂ��Đ�������B
Step1: �A�����������쐬����
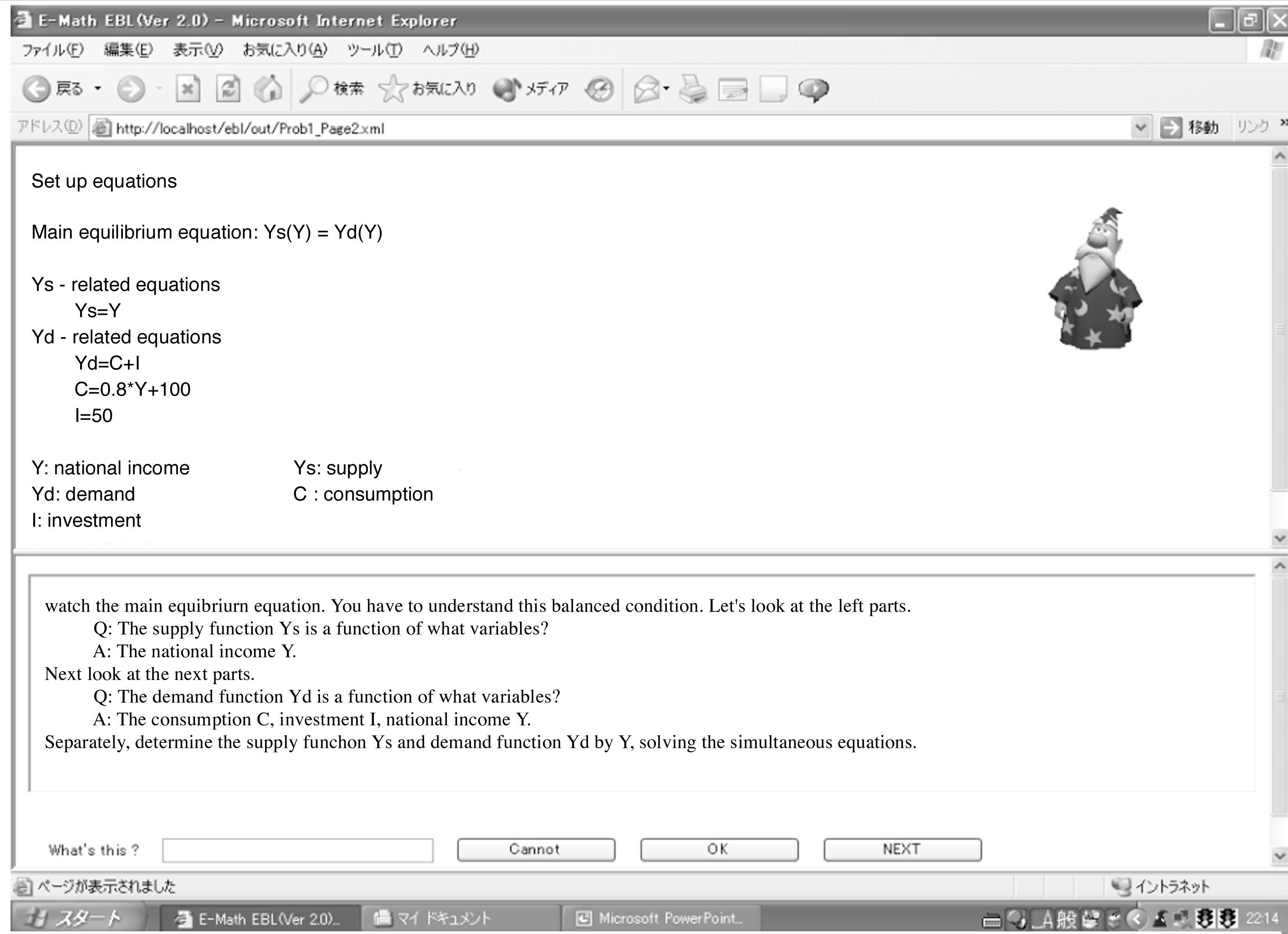
�����ׂ��A�����������쐬����i�}4�Q�Ɓj�B���̖��ł́C���s��ɂ�����u�������iYs�j �������v�iYd�j�v�ɒ��ڂ���B���̋ύt�������C���ύt���ƌĂ�.���C���ύt���Ƃ����Ӗ��ɑΉ�����XML�^�O�̒�`�ɂ��Ă͎��߂ŏq�ׂ�B�A���������̎��́C���̃��C���ύt���̍��E�ǂ��瑤�̐��E�ɊW���鎮�ł��邩�ɂ���āC2�������B�܂��CYs�Ɋւ��鐢�E�ł��邪�C�������iYs�j�͍P���I�ɍ��������iGDP:Y�j�ɓ������B����CYd�Ɋւ��鎮�͐��{����C�C�O������l���邩�ۂ��Ɉˑ����Ċe��̃��f�������s����B���̖��ł́C���{����y�ъC�y287�Łz�O������l���Ȃ��P����Yd=C+I�Ń��f�������Ă���B�b�͏���iConsumption�j�CI�͓����iInvestment�j��\�킷�ϐ��ł���B
�@
�@
Step2: ���ӂ̊������߂�
���ɁC���C���ύt���̍��ӂƉE�ӁC���ꂼ��ɂ��ė^����ꂽ�ϐ��������Ƃ�����ƂȂ�悤�ɘA���������������B���̖��ł́C���ӂ�Ys��Ys�iY�j�̌`�̊��ƂȂ�悤�Ɍv�Z����B���ʂ́CYs=Y�ł������B���̗�ł́C1�������Ȃ��̂Ōv�Z�s�v�ł���B���̊����ɂ̓����N�������Ă��āC�N���b�N����ƃO���t���\�������B
Step3: �E�ӂ̊������߂�
���ɉE�ӂ̎�Yd�ɂ���Yd�iY�j�����߂�B���ʂ́CYd=0.8*Y+150�ł������B
Step4: ���C���ύt�����^�[�Q�b�g�ϐ��ɂ��ĉ���
�ȏ�Ń��C���ύt���̍��ӂƉE�ӂ̎����C�^�[�Q�b�g�ϐ��ɂ���ĕ\���ł����B���ɁC���C���ύt���̗��ӂɂ��̎��������āC�^�[�Q�b�g�ϐ��̋ύt�l�����߂�B���̖��ł́CY=750�ł������B
Step5: ����ϐ��̕ϓ��ɂ��ύt�l�ւ̌��ʂ��݂�
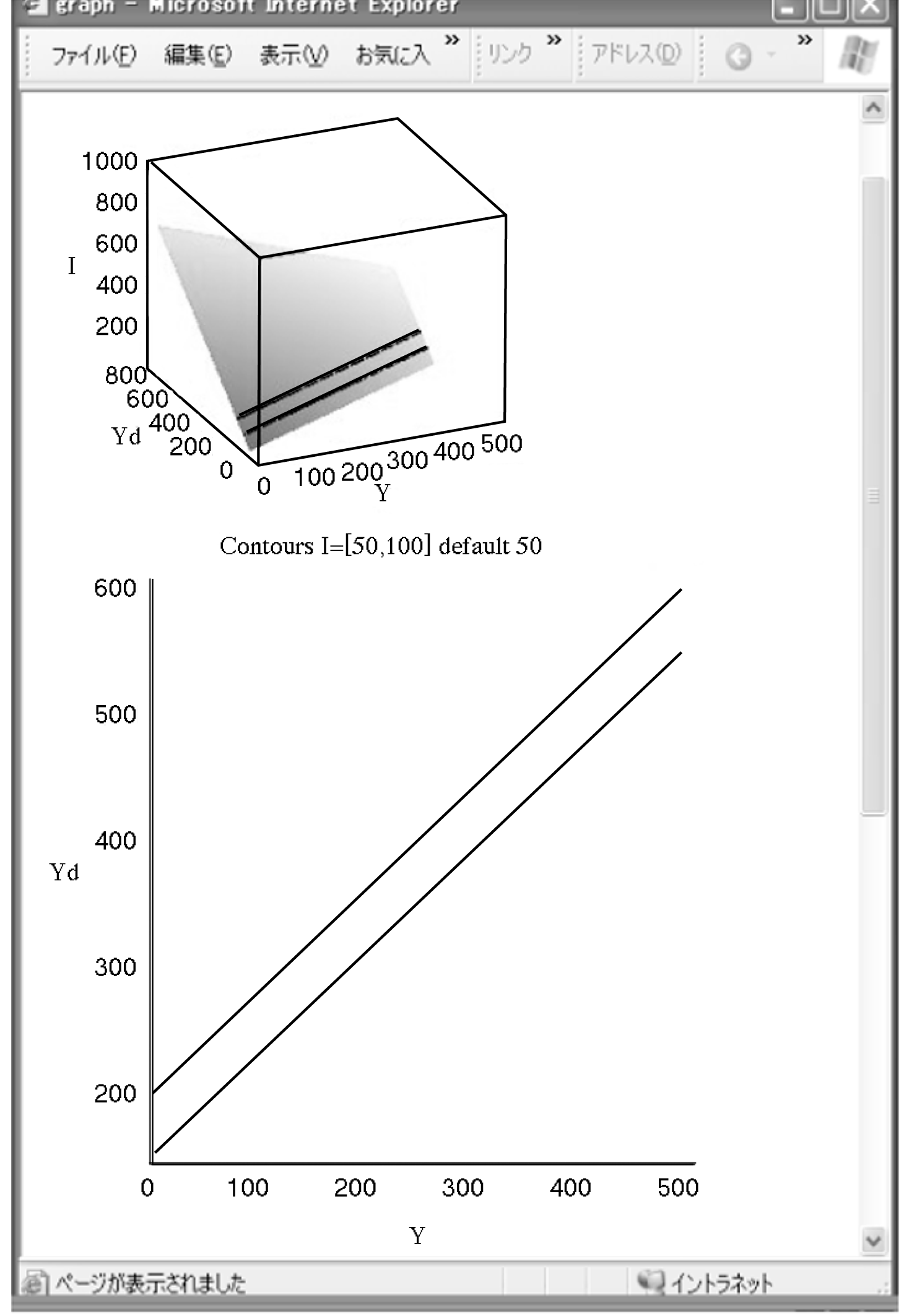
���悢�����ϐ���ϓ������ă^�[�Q�b�g�ϐ����ǂ̂悤�ɕω����邩�ׂ�B���̖��ł́C�����iI�j��I=50����I2=100�ɑ���������Y�ւ̌��ʂ����Ă���i�}5�Q�Ɓj�B�{�^��"Go"���N���b�N����ƁC�}6�̃O���t���\�������B���ނƂ��Ẵ|�C���g�́CI�y��I2=I+��I��2�l�y288�Łz�ɑ��āC3�����I��Yd�iY,I�j�̋Ȑ��������Ă���_�ł���B��X��Web���ނł́C���C���ύt���̉E�ӂ̎����邢�͍��ӂ̎����^�[�Q�b�g�ϐ��i���̖��ł�Y�j�ȊO�̕ϐ��i���̖��ł�I�j���܂�ł����ꍇ�i�܂�CYd=Yd�iY,I�j�̂悤�ȏꍇ�j�C3�����O���t��`���Ƃ�����@�v���Z�X�Ƃ����B���̗�ł́C���Web�y�[�W�Ŏw�肵��I=50�����I=100��2�{�̓��������`����Ă���B�w���́C����3�����O���t��Θb�I�ɁC���_��ς��Ȃ��瓮�����Ȃ���O���t�\�����邱�Ƃ��\�ł������CYd�`Y�̕��ʂ��ォ��`�����ꍇ�C�}6�̉��ɂ���悤�ȕ��ʏ��2�{�̋Ȑ��ƂȂ�B�}6��Maplet�ɂ���č쐬���ꂽ���̂ł���B
�@
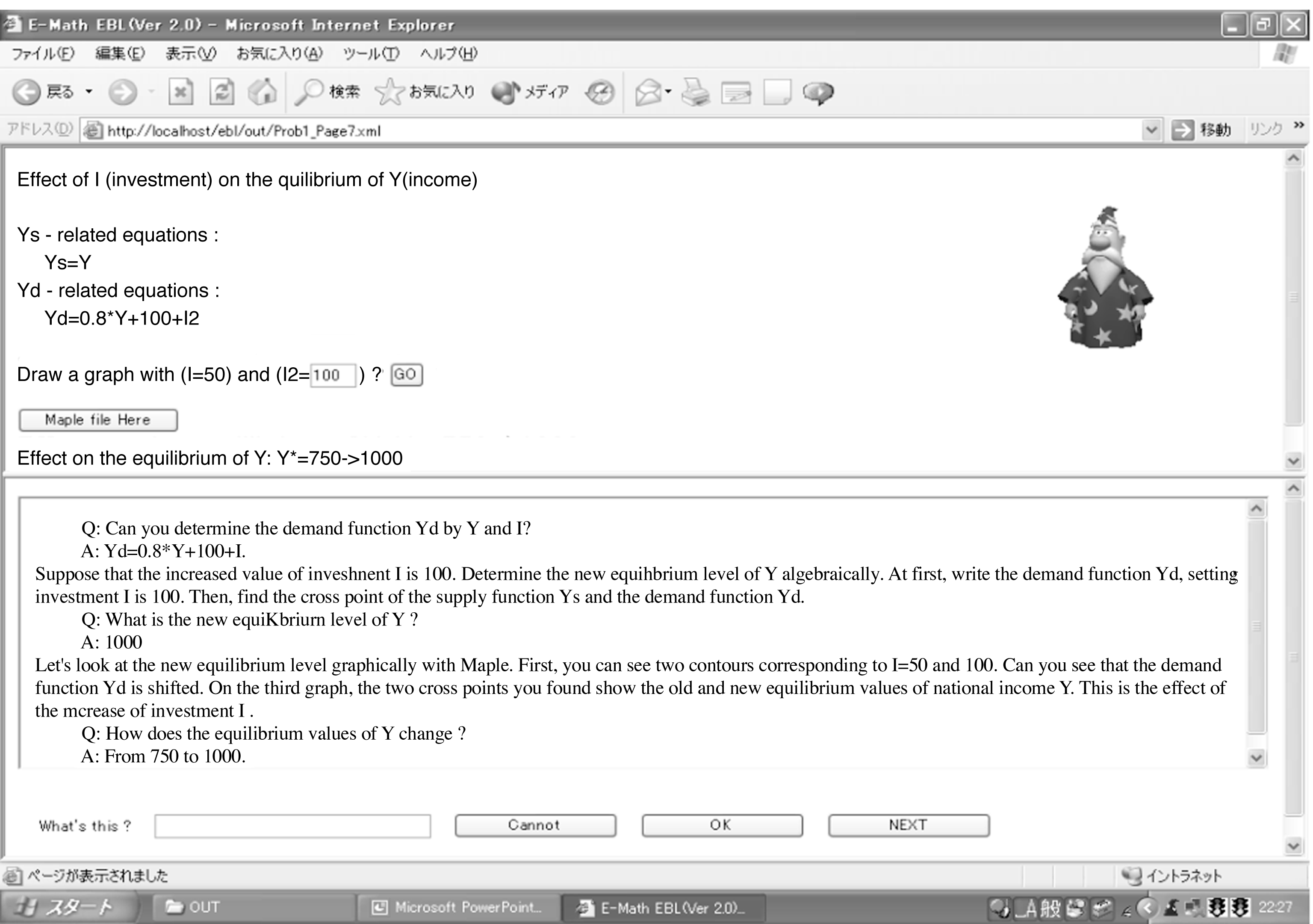
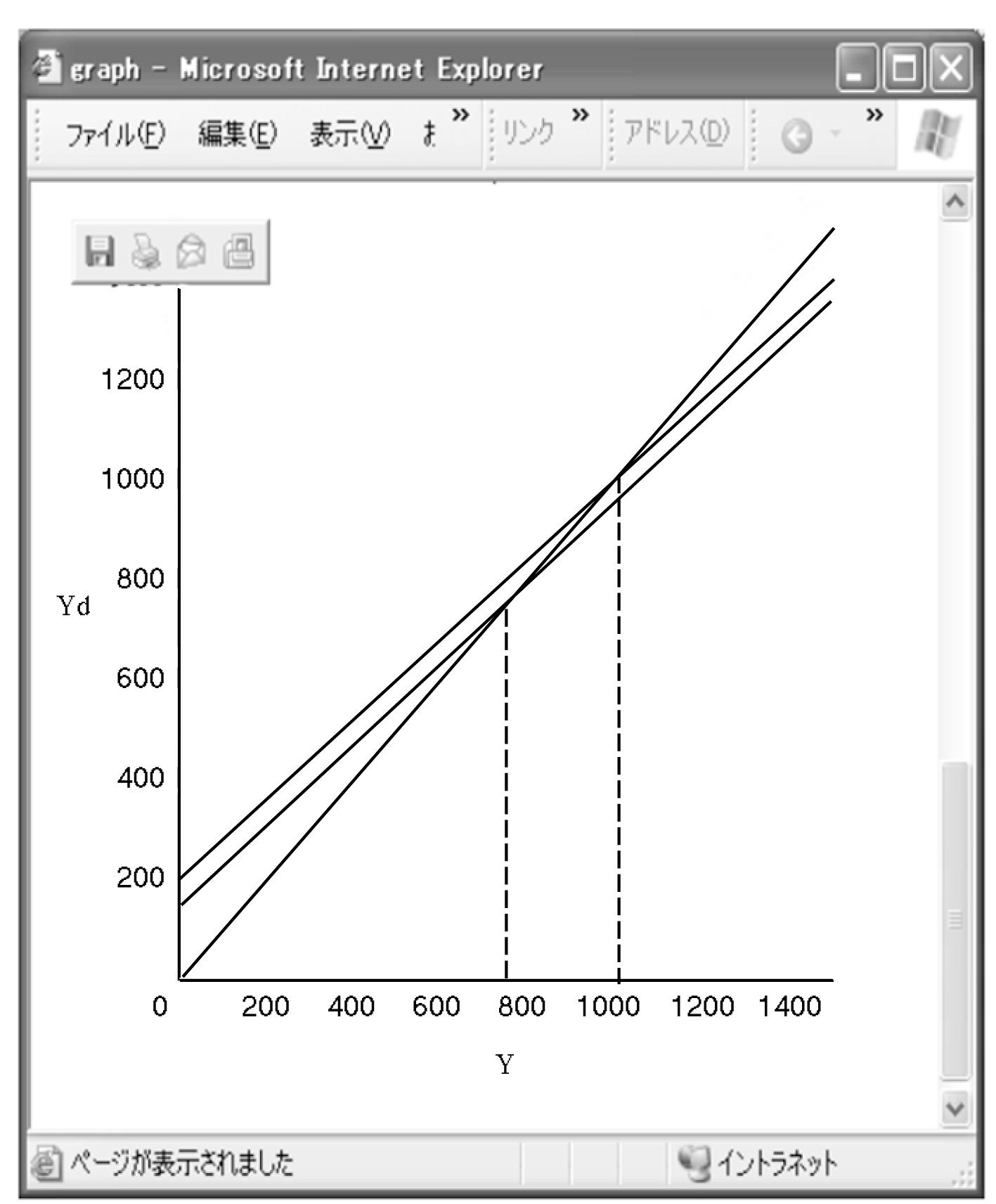
����ɁC��ɋ��߂���_�̐}�ɑ��āC����2�{�̓�������NjL���邱�Ƃɂ��C�}7�̂悤�ȋύt�l�ւ̌��ʂ�������B���̗�ł͋ύt�lY*��750����1000�ɑ������Ă��邱�Ƃ�������B�w���̓O���t�������œ������Ď��_��ς��邱�ƂŁC���̌��ʂ͐}5�Ɏ������㐔�I�ɉ��������ʂƓ����ł��邱�Ƃ��m�F�ł���B
Step6: �ϐ��ϓ��̔g�y�v���Z�X���݂�
�ϓ��������ϐ��ƁC�^�[�Q�b�g�ϐ��̋ύt�l�̕ω��ւ̔g�y�v���Z�X���C���ɒǂ��Ď����B����ϐ��̕ϓ��ɂ�葼�̕ϐ��������ǂ���̕����ɕϓ����邩���C���C���ύt���̍��ӂɂ�����g�y���ʁC���ɁC���ӂ���E�ӂփ^�[�Q�b�g�ϐ�����Ă̔g�y�C�E�ӂɂ��ւ�g�y���ʁC��2�̐��E�����Č��ʂ�������邱�Ƃɂ��C�w�������̔g�y�v���Z�X�̏ڍׂ𗝉����y289�Łz����悤�x�����Ă���B
����Web���ލ쐬���j�y�э쐬���ꂽ���w���ނ̓����́C�ȉ��̓_�ł���B
�i1�j�A�����������̎��W�����C���C���ύt���̍��ӂƉE�ӂɂ����2�����邱�ƂŁC���ŗ^����ꂽ�ϐ��Ԃ̊W�����ʂ��̂悢���̂Ƃ��Ă���B
�i2�j�ϓ��������ϐ��Ƃ��̍�����2�{�̓�������3�����I�ɃO���t�\�����C������w���Ɏ��_��ς��ē������Ă��炤���ƂŁC�ϐ��̕ϓ��̑��̕ϐ��ւ̌��ʂ�}�I�ɕ\���\�B
�i3�j�ϐ��̕ϓ��̔g�y�v���Z�X�����C���ύt���̍��ӂƉE�ӂ̊ԂŁC�ǂ̂悤�Ɍ��ʂ��g�y���Ă����̂��X�e�b�v�o�C�X�e�b�v�ɐ�������̂ŁC�w���̗������e�ՂɂȂ�B
���ɖ{�����������̃��^���x���L�q�t�@�C���������C������������B���^���x���L�q�t�@�C���͈ȉ��̂悤�ɂȂ�B����œ��͏��Ƃ��ď\���ł��邱�Ƃ̐��w�I�����ɂ��Ă͊��ɍs����12�B
data: nationalIncome, Y, ,Y>0
data: supply, Ys, ,Ys>0
data: demand, Yd, Yd>0
data: consumption, C, C=0.8*Y+I, C>0
data: investment, I, I=50, I>0
unknown: nationalIncome
given: consumption, investment
relationship: Ys=Y, Yd=C+I
�y290�Łzfind: equilibrium (Y, Ys=Yd),
effectOfvariance (Y, I, Ys=Yd)
���ނ͈ȉ���2�̉�@�v����������\�������B
�i1�j�ύt�l�����߂遨 equilibrium�i�j
�i2�j����ϐ��ϓ��̉e�����݂遨 effectOfvariance�i�j
��X�̓V�X�e���E�X�[�p�[�o�C�U�[�Ƃ��Ă���2�̉���v���Z�X���f������ы��t�Θb���f����Perl�ō쐬�����B
�@
�@
4�D���w���ɂ�����Ӗ��I��XML�^�O
�{�߂ł͉�X�������Ă���悤�ȃ}���`���f�B�A���w�p���ޒ�`�ɂ��ĕK�v�ƂȂ�XML�^�O���C���C�A�E�g��`�p�Ɩ��̈Ӗ���`�p��2��ޕK�v�ł��邱�Ƃ�������C��������������ł͂ǂ̂悤�ɈӖ��IXML�^�O���`���������������B
4.1�@���C�A�E�g��`�pXML�^�O
�Œ�I�ȉ�ʂ̃t���[���Ƃ��Ĉȉ����`�����B
�y291�Łz�i1�j���G���A�ibb area�j
�i2�j�Θb�G���A�iinteraction area�j
�i3�j�w�����̓G���A�istudent input area�j
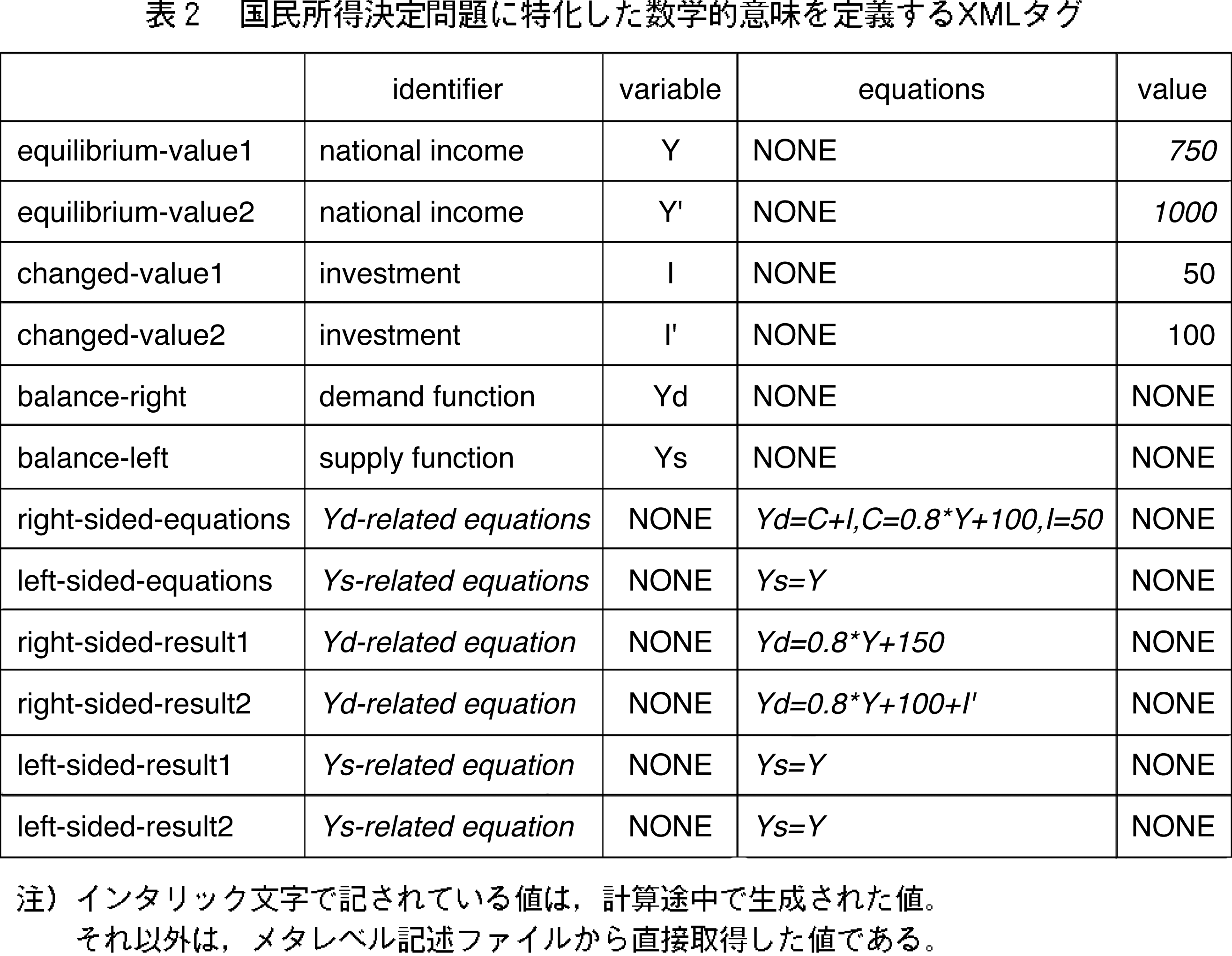
��`����XML�^�O�̎�Ȃ��̂�\2�Ɏ����B���G���A�ɂ́C����������̕��͂��\�������B�ǂ̕����������ł��邩������<expr>�^�O���`�����B���̃^�O�l�͏���"Q^3+2*Q^2"�̂悤�Ƀe�L�X�g�ŏ�����邪�C�����\���p�t�B���^��ʂ��ƁC���̐��������̐Î~��t�@�C������������C<img>�Ƃ���XML�^�O�ɂ���Ă��̐Î~��t�@�C�����Q�Ƃ����悤�ɂȂ��Ă���B�܂��C�Θb�G���A�̓`���b�g�V�X�e���̂悤�ɉ�b�������X�ɕ\�������B���t�̉�b�͉��z�L�����N�^�����������B�����<Q>��<A>�Ƃ�������Ɖp��XML�^�O�ɂ���Ē�`�����B�����Œ�`�����^�O�͉�ʃ��C�A�E�g�ƑΘb�̗���Ɋւ�����̂ł���C�ΏۂƂ��鐔�w���̈Ӗ��ɑΉ�������̂ł͂Ȃ������B
4.2�@���w���̈Ӗ��I�^�O
���w���u�`����ہC�u�������C���̋ύt�����v�Ƃ��C�u�������ӎ���������Ɓv�Ƃ����悤�ɁC���̐��w���ɂ�����Ӗ��Ő������邱�Ƃ������B�����̏ꍇ�l�ԋ��t�́C���̌ŗL�̖����ł���͋�̓I�ɉ����w���Ă���̂��C���̕ϐ����y�ѐ����Ȃǂ��ȗ����邱�Ƃ������B���邢�́C�t�ɁC��̋�̓I�\������ėp���f�����w���ɑz�N�����悤�Ƃ���B�܂�l�ԋ��t��generalization��specialization���w���̔��������Ȃ���C�_��ɍs���Ă���B�V�X�e���ɂ���generalization��specialization�Ƃ̎��R�ȍs��������点�邽�߂ɂ́C���w���̈Ӗ��I�ȃ^�O���`����K�v������B
��X�͍�������������ɂ�����Ӗ��I�^�O���ǂ̂悤�ɒ�`��������������i�\2�Q�Ɓj�B�\2�ł�1�s����̊T�O���^�f�[�^�ɑΉ�����4�̑���XML�^�O�������Ă���B�d�v�ȃ��^�f�[�^�Ƃ��āC���C���ƂȂ�ύt���C�����āC���̍��Ӂibalance-left�j�C�y�сC�E�Ӂibalance-right�j�C�y292�Łz�ύt�ϐ��iequilibrium-value�j�Ȃǂ�����BEquilibrium-value1�y��2�́C���V�t�g�̑O����Ӗ�����B���z���t�̉�b�e���v���[�g��XML��ŏ��߂����̖��Ӗ��IXML�^�O�Ƃ��Ē��ۓI�ɏ������B����XSLT��̃}�b�s���O�����ɂ���̓I�Ȓl����������B�}3�̑Θb�G���A�ɉ��z���t�ɂ���b���\������Ă��邪�C�����̕��͂ɂ͒�`���ꂽ�^�O�����p����Ă���B
�@

�@
�@
�ʂȐ��w���^�C�v�ɑ��Ă��̂悤�ȈӖ��I�ȃ^�O��`���s�����Ƃ͈Ӗ������邩�l�@����B���Ȃ��Ƃ��V�X�e���̃v���O������\2�̂悤�ɈӖ��I�^�O���`���邱�Ƃ͌�������Ɍq�������B��X�͍���������������Ɏ��삵���œK�����̂悤�Ȕ��ɓK���͈͂̍L�����^�C�v�Ɋւ��Ă͂��̂悤�ȈӖ��I�^�O��`���s�����Ƃ͈Ӌ`������ƍl����B��������ƁC���̂悤�ȈӖ��I�^�O�̕\���w���̓��̒��ɍ\�z���邱�Ƃ��C�w�K�Ƃ��Ă��̖��𗝉��������ƂɂȂ�ƌ����悤�B�܂肱�̖��̖{���ł���i�o�ρj���f���̈Ӗ������^�f�[�^���x���Œ�`�������ƂɂȂ�B
���w���ނ�XML�y��XSLT��p���Ď����������錤���͂���13�B��������X�̂悤�ɁC��莿�̍������t�̃K�C�_���X������ڎw���Ė��̈Ӗ��ɑΉ�����XML�^�O���`������͂Ȃ��BIEEE LOM�iLearning Object Metadata�j14�Ȃǂ̋��ލ쐬�p���^�f�[�^�ɂ����ẮC���ނ��\������v�f�̒�`�͂Ȃ���Ă��邪�C���w�̓���̃^�C�v�̖��ɏo������Ӗ��C���邢�͊T�O�ɑ��郁�^�f�[�^���`����Ƃ��������͂܂��Ȃ��B���w���̈Ӗ��I���^�f�[�^��`�Ɋւ��錤���Ƃ��āC�M�҂��s���Ă���ȊO�ł́C�����̒ߋT�Z�ɂ����郁�^�f�[�^��`�����邾���ł���15,16�B���������w���ɂ����郁�^�f�[�^���`���邱�Ƃɂ��C���̃��^�f�[�^�ɑ��āC���t�C�O���t�C�ȂNJe��̐����p�\���f�ނ����邱�Ƃ��\�ł���C���͑�̈Ӗ���`���^�f�[�^�𗘗p���邱�ƂŁC����Ɏ��̍����K�C�_���X���\�ƂȂ�B���w�y293�Łz����`�p���^�f�[�^�̂���Ȃ錤�����]�܂��Ƃ���ł���B
5�D�܂Ƃ�
�{�e�ł́C��X���J�����Ă���e-Math Interaction Agent�Ƃ������w��莩�������V�X�e���̍������������萶���v���Z�X�ɂ��Đ��������B�܂��C��X����Ă��鐔�w�p���ނ̎��������Ɋւ���ėp���f������������B�����Ă�����ǂ̂悤�Ɏ������邩�C�ėp�̃V�X�e���\�����q�ׂ��B
�����Ď��������������ގ���Ƃ��āC��������������pWeb���ނ��Љ���B����Web���ނ̖������v�����y�сC�����̂��߂̃X�L�[�}�́C��ʓI�Ȗ��u�A������������2�ϐ�A�y��B�̊ԂɁC���̑��̓Ɨ��ϐ�X�����ύt�WA(X) =B(X) ������ꍇ�C�ύt��Ԃ�X�̒l���C���̕ϐ��̕ϓ��ɂ��ǂ̂悤�ȉe�����邩�H�v�ɑ��L���K���\�ł���B�܂��Ă���Web���ނ̉�@�v�����y�ѐ����X�L�[�}�͓K���͈͂��L���B�������C���̍�������������͂����܂Ŏ���ł���B���̗�ɂ����āC�ǂ̂悤�ɈӖ��I���^�f�[�^���`���������|�C���g�ł���B���݁C����v���Z�X���f���y�сC���t�Θb���f���̓V�X�e���E�X�[�p�[�o�C�U�[�������ŏ����Ă��邪�C�����I�ɂ́C�w���̔����ɍ��킹�ē��I�ɑΘb���e���v���[�g�Ȃǂ��\�������B���̂��߂ɂ��{�_���ŏq�ׂ����w���̈Ӗ��I���^�f�[�^�̒�`�͕K�{�ƍl����BIEEE LOM�Ȃǂ̋��ލ쐬�p���^�f�[�^�ɂ����ẮC���ނ��\������v�f�̒�`�͂Ȃ���Ă��邪�C���w�̓���̃^�C�v�̖��ɏo������Ӗ����邢�͊T�O�ɑ��郁�^�f�[�^���`����Ƃ��������͂܂��Ȃ��B���������w���ɂ����郁�^�f�[�^���`���邱�Ƃɂ��C���̃��^�f�[�^�ɑ��āC���t�C�O���t�C�ȂNJe��̐����p�\���f�ނI�ɐ������邱�Ƃ��\�ł���C���͑�̈Ӗ���`���^�f�[�^�𗘗p���邱�ƂŁC�e�푽�l�Ȑ��������Ă����C����Ɏ��̍������ނ������\�ƂȂ�B��X�͍�������w���̈Ӗ���`�p���^�f�[�^�ɂ��Č����𑱂��鏊���ł���B
�ӎ�
�{�����̈ꕔ�́C����15�N�x�Ȍ����Ռ����iC�j�i2�j�u�}���`���f�B�A����x���V�X�e��eMath�ɂ����鋳��p�f�[�^�x�[�X�̍\�z�v�i�ۑ�ԍ��F15606014�C��\�F���c�R�����j�ɂ��B�����ɋL���Ďӈӂ�\���܂��B�܂����w�ƌo�ς̗̕���𗝉������^���x���ȃv���O���~���O�������Ă��ꂽ�c粖q�q���Ɋ��ӂ��܂��B