【33頁】

レベニューマネジメントにおける統計的手法

福地　純一郎＊, 砂見　しづゑ†

概　要

レベニューマネジメントにおける統計的手法をホテル業を例にとって概観する. 特に, ブッキングデータによって将来の予約客室数および販売客室数を予測する方法について, 確率モデルを仮定した上で詳細に論じる. また, 打ち切られた客室需要量データから確率分布のパラメータを推定する方法についても述べる.

１　序論

レベニューマネジメント（Revenue Management, 以降RMと呼ぶ）とは, 基本的には同一のリソースを利用した商品の価格および割当量を変化させることにより, 売上高を増加させるためのORの手法の体系である. RMは米国の航空業界において, 1978年のディレギュレーション以降, 著しい発展をとげてきた. さらに, 航空業と同様のの収益構造を持つ他の輸送業およびホテル業においても導入と発展が進んでいる. これらのビジネスは以下のような共通する収益構造を持つ.

1．リソースの容量に上限が存在する.

2．在庫はある日時を過ぎると無価値になる, 陳腐化在庫（perishable inventory）である.

3．固定費が高い.

4．可変費が低い.

5．季節, 曜日, 一日の時間, 周辺のイベントなどに応じて需要の変動が激しい.

6．将来の需要をある程度の精度で予測することが可能である.

RMの包括的な書物Talluri and van Ryzin (2004) では, 小売業におけるディスカウントの手法などもRMに含まれており, 上記のような特徴をRMの適用範囲の必要条件とはしていない.

RMに関する総合的な解説については, Cross (1997), Ingold, et. al. (2000), Talluri and van Ryzin (2004) などの書物, Kimes (1989), McGill and van Ryzin (1999) などの解説論文を参照せよ.

RMでは最適化法などORの手法とともに, 統計的手法が重要な役割を果たす. RMにおける統計的手法の利用例としては, 予約客室数および販売客室数の予測, キャンセル数予測, ノーショウ数予測などが挙げられる. これらの予測の精度を上げることによってホテルのサービスおよ【34頁】び利益の向上に結びつけることができる. 本論文では特に, 予約客室数と販売客室数の予測方法を詳細に説明する.

２　ピックアップ・モデルによる販売客室数および予約客室数の予測

Weatherford and Kimes (2003) によれば, 販売客室数の予測方法は主に以下の3種類である.

1．販売客室数の時系列データを用いる予測

2．予約客室数の時系列データ（ブッキングデータ）を用いる予測

3．上の2つ方法による予測値を合わせる方法

Weatherford and Kimes論文は2つのホテルチェーンのデータを用いて, 7つの予測方法の事後的精度を比較している. 本節では2のブッキングデータを用いた予測法を詳細に説明する.

2.1　ブッキングデータ

ある特定の日に宿泊するための予約客室数の時系列データをブッキングデータと呼ぶ. 通常最初の予約が入った日から宿泊当日まで毎日, 一日単位で入った予約数とキャンセル数が記録される. 一定期間中の予約数の増分をピックアップ（pick up）といい, 販売客室数の予測で重要な役割を持つ. ピックアップの値は計測期間の取り方によって変わる. 本論文ではこの期間をピックアップの期間と呼ぶことにする. 以下ではピックアップの期間を1週間として説明をする.

予約客室数は宿泊日までの時間をインデックスとして表すと分析する上で便利である.

まず, 予測対象となる宿泊日の販売客室数をで表す. ただし販売客室数とは宿泊当日の晩に決まる客室の販売数を意味する. 宿泊日の1週間前におけるオンハンドの予約客室数をで表す. 同様に週間前におけるオンハンドの予約客室数をで表す. したがって予測対象となる宿泊日のブッキングデータは

と表される. 予測対象宿泊日からちょうど週間前の日に宿泊するための, 宿泊当日から週間前におけるオンハンドの予約客室数をで表す. つまり週間前宿泊のブッキングデータは

と表される. また宿泊当日週前から週前までのピックアップをで表す. つまりは

【35頁】

で定義される. 本論文では, 記号を必要以上に複雑にしないために時間のインデックスの単位とピックアップの期間を一致させている. ピックアップの期間としては, 1日, 1週間, 2週間, 1ヶ月などが考えられ, それぞれの期間に応じて以下で述べる分析手法の詳細が異なるので注意が必要である. 3.1節で述べる需要増分の平均の推定方法もピックアップの期間によって手法の詳細が変わる.

以下では, ピックアップの期間が1週間のピックアップ法（pick-up method）について説明する. ピックアップの期間を1週間とする場合, 宿泊当日からちょうど1週間の整数倍前の時点からの予測は可能であるが, それ以外の時点からの予測は多少複雑になるという決定がある. しかし, ピックアップの期間が1週間のときには, 需要増分の確率分布が正規分布などの連続型確率分布で近似されることが多いので, センサーデータの扱いかたが比較的容易である. ピックアップの期間を1日にすることの長所は, 宿泊当日何日前からでも予測が可能であることである. これに対して, ピックアップの期間が1日である場合, センサーデータの分析が煩雑になる可能性がある.

ピックアップ法による予測を説明している論文としてGorin (2000), Zeni (2001), Weatherford and Kimes (2003) などがある. しかし確率モデルを定式化して予測を論じた文献が見当たらない. 以下の節では, 予約客室数の確率モデルを記述した上で, 予約および販売客室数の予測方法を説明する.

2.2　加法的ピックアップ法

同じ曜日の宿泊予約数（Booking）データが利用可能とする. そのうち個のデータはすでに closed の宿泊予約数データである. 現時点から日後の宿泊日の販売客室数と現時点から宿泊日前日までの毎日の宿泊予約数（On hand のブッキング数）を予測することが目的であるとする. 宿泊当日以前の宿泊予約数の予測値は, オーバーブッキングポリシーや販売促進の方法を決定する上で有用である.

ここでの目的は予測対象の宿泊当日から週前の時点において

を予測する方法を考察することである. これはいわゆるブッキングカーブ１の残りの部分を予測するということである.

予測対象の宿泊日週間前（以下では簡単に第週と言うことにする）の宿泊日の, 宿泊当日日前のオンハンドの宿泊予約数をで表すとする.

ホテルの客室総数は固定されているので, 時点における個人客予約客室数はからグループ客予約客室数を除きオーバーブッキング数上限値を足した値

　　　　　(1)

【36頁】を超えない. この上限値は通常ブッキングリミットと呼ばれる.も確率変数とみなすのが自然である. したがって

が成り立つ. 時点におけるオーバーブッキング数上限値の決め方はRMにとって重要であるが本論文では扱わない. 詳しくは Talluri and van Ryzin (2004), Chapter 4を参照せよ.

ブッキングリミットが存在することから, ピックアップにも上限値が存在する. 週前のピックアップの上限値はブッキングリミットから前日までの予約数を引いた値

　　　(2)

である.

次に予約客室数の時間的変化を表す確率モデルを記述する.

は初めて予約が入る週を表すとする. も本来確率変数とするべきであるが, ここではに依存する定数であるものとする. 次に, は週前から週前までに入る需要（つまり, 仮にブッキングリミットがない場合に入る予約数）を意味する確率変数であるとする.

これらの変数を用いて, 予約客室数とピックアップの間に以下のようなモデルを仮定する.

　　　(3)

　　　(4)

ピックアップは以下のように決定される.

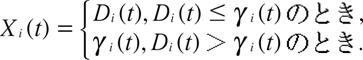　　　(5)

(5) 式は, 需要増分がピックアップの上限値を超えたとき, 需要増分の値が打ち切られる（センサーされる）ことを意味している.

確率変数列に対して以下の仮定をする.

仮定1：各に対して, は独立に同一の確率分布にしたがう.

仮定2：各に対しては独立で, 周辺確率分布は同一であるとは限らない.

また

【37頁】

と書く. 仮定1, 2よりも弱い仮定を考えることも可能であるが, 仮定1, 2のもとで理論の構築が行いやすいので本論文ではこの2つの仮定が成り立っているものとして議論する.

(3), (5) で記述されるモデルを加法的ピックアップモデルとよぶ.

次に加法的ピックアップモデルに基づく予測法の説明をする.

宿泊当日週前の予約客室数から1週間後の予約数を予測したいとする. 宿泊当日日前の予約客室数は

　　　(6)

と表される. したがっての自然な予測量は

　　　(7)

である. ただしはの推定量である. またはの最小値を意味する.

の求め方, つまりの推定方法にはいくつかの方法が考えられるが, 代表的なのものを第2.4節と第2.5節で述べる. (7) 式と同様の式を用いて, から逐次予測量が得られ, 結局の予測量

を得る.

2.3　乗法的ピックアップ法

乗法ピックアップモデル（multiplicative pick-up model）は以下の式で表される.

　　　(8)

ただしは正の値をとる確率変数である. 両辺の対数をとれば

　　　(9)

となり,についての加法的モデルになる. と書けば

　　　(10)

【38頁】となる. の自然な予測量は

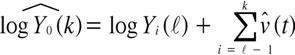　　　(11)

である. ただし, はの推定量である. の自然な予測量は

　　　(12)

で与えられる．

2.4　古典的ピックアップ法

予測量 (7) を得るために, 需要増分の期待値の推定量が必要である. 仮定1のもとでは過去の需要増分の標本平均がの推定量として適当である. 2.4節と2.5節では, 過去の需要増分は打ち切られていないことを仮定して説明する. この場合であるから, すべての需要増分は観測されており, 過去のピックアップの標本平均でを推定すればよい. 過去の需要増分が打ち切られるている場合のの推定方法は3節で扱う.

予測の時点と同一の日および予測時点以前の宿泊日のブッキングデータだけを利用してを推定する方法は古典的ピックアップ法（classical pick-up method）と呼ばれている.

予測対象の宿泊日から週間前の同じ曜日までのブッキングデータが利用可能であるとする. このとき, 完備なブッキングデータ（complete booking data）としては

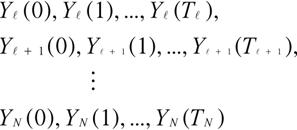
までが利用可能である. したがっては

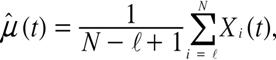
で求める.

2.5　発展的ピックアップ法

の推定に, まだ宿泊日が来ていないブッキングデータも用いる方法があり, これは発展的ピックアップ法（advanced pick-up method）と呼ばれている. このとき, 部分的ブッキングデータ（partial booking data）としては

【39頁】

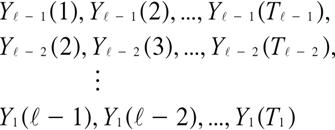
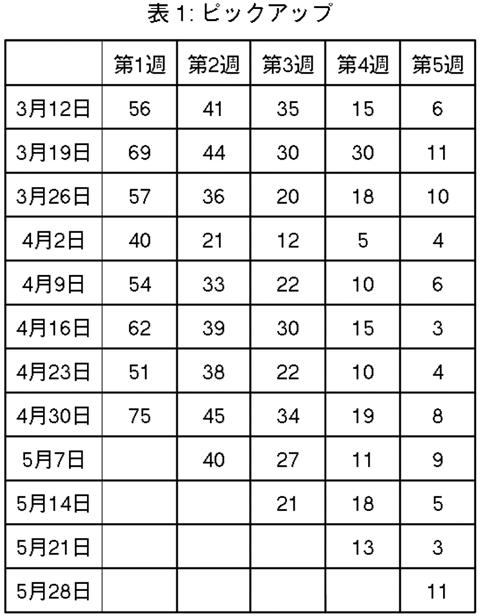
が利用可能である. 表1はピックアップの架空データで, 完備ブッキングデータと部分的ブッキングデータの例である. 表1列目は宿泊当日の日付を表す. 表1行目は宿泊当日から何週前かを表す. この表のピックアップ値の記録時点が4月30日夜で, 5月28日からちょうど4週前の時点である. たとえば4月30日宿泊の宿泊前の1週間のピックアップは75である. 空白部分は, まだその時点に到達していないためにピックアップがわかっていないことを意味する.

各に対して

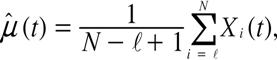
と定義する. これらのを（7）式に代入して得られる予測が発展的ピックアップ法による予測である.

以下に挙げるのはピックアップ法による予測量の基本的な性質であり, 実際に予測をする際に知っておく必要がある.

1．リードタイムが大きいほど予測誤差分散は大きくなる. つまり予測の精度は悪くなる.

2．が大きいほど, 不完備なブッキング系列の個数が多くなるので, 発展的ピックアップ法と古典的ピックアップ法の予測誤差分散の差が大きくなる.

【40頁】

３　データの打ち切り（Censoring）

リソースに上限がある場合, 販売量は上限値を超えることができないので, 販売量が需要量と一致するとは限らない. 販売量が上限値に一致する場合, 需要量は販売量を上回っていたと考えられる. このようなデータをセンサーデータ（censored data）という. センサーデータをどのように扱うかはレベニューマネジメントにおける重要な問題の一つである.

3.1　客室需要の平均の推定

一定の条件下における客室需要の確率分布の平均を推定する方法を説明する２.

ホテル客室販売量のデータから客室需要の確率分布の平均を推定することを考える. 以下では, 簡単化のためをで表す.

一つのホテルの客室総数は固定されているので, 個人客用に販売できる客室数には上限が存在する. 上限の値をで表す. この上限値は通常ブッキングリミットと呼ばれている. はたとえば

　　　(13)

で与えられる. ただしは個人客以外（グループ客, 無料扱い客など）による客室販売数である. つまり

が成り立つ. つまり販売量は上限値の制限を受けており, 真の需要量とは異なる. したがって販売量そのものの平均は需要量の平均をを過小推定することになる.

まず打ち切り（censoring）が生じるモデルを与える. 第宿泊日の真の需要をで表す. は独立で

であると仮定する.

客室販売量は以下のように定まる.

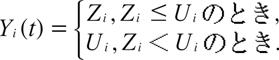
このように, 需要の確率分布のパラメトリック形が既知のときにはパラメータの推定に最【41頁】尤法が用いられることが多い. センサーデータが存在するときに最尤推定量を求める一般的な方法が Dempster, et. al. (1977) によるEMアルゴリズムであり, RMでも用いられることが多い. 以下では需要量の確率分布が正規分布のときのEMアルゴリズムについて説明を与える. 確率分布が他のパラメトリック族のときには, 用いる公式が変わるだけで基本的方法は同じである. まず

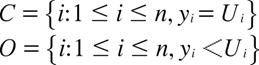
と定義する. はセンサーされている需要の添え字の集合, はセンサーされていない（観測されている）需要の添え字の集合である. が与えられたときの尤度関数は

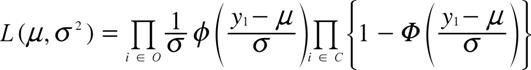　　　(14)

で与えられる. ただしはそれぞれ標準正規分布の確率密度関数, 確率分布関数である.

尤度関数を最大にするの値を最尤推定値という. 尤度関数（14）は複雑であり最適解（最大にする解）を数値的に求めることが困難であるので, EMアルゴリズム３を用いる. このとき以下の公式が必要になる.

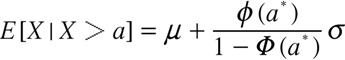　　　(18)

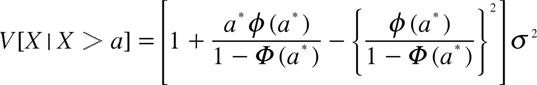　　　(19)

ただし

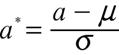
である. EMアルゴリズムは以下のステップで記述される. と書く.

ステップ1：センサーされていない販売客室数だけを用いた標本平均, 標本分散を初期値とする. とする.

ステップ2：

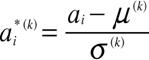
と置き,

【42頁】

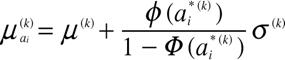
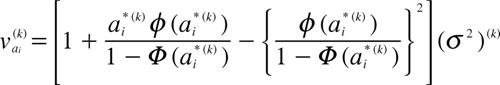
を計算する.

　　　(20)

を計算する.

ステップ3：

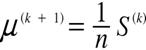
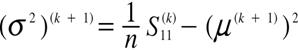
を求める.

ステップ2と3をパラメータ推定値が収束するまで繰り返す.

3.2　客室需要増分の平均の推定

ピックアップ法による販売客室数の予測は一定期間に発生する需要の増分の予測に基づいているので, 需要増分のセンサーデータの扱いが重要になる.

時間における追加的ブッキングつまりピックアップは, から時間における個人客予約数を差し引いた

　　　(22)

を超えることができない. つまり時間のピックアップをで表せば

が成り立つ. つまりピックアップは上限値の制限を受けており, 真の需要量増分とは異なる. したがってピックアップそのものの平均は将来のピックアップを過小予測し, それを用いたピックアップ法の予測は過小予測になる.

【43頁】一つの方法として日次ベースで宿泊予約を断った件数のデータ（denial data）を利用する方法が考えられる. しかし Zeni (2001) は Denial data を取得することが難しく, 取得できてもその信頼性は低いことが多いと述べている.

3.2.1　代入法

EMアルゴリズム以外の簡便な方法を説明する. これらの方法については Zeni (2001) が詳しい. まずセンサリングデータがあることを無視した通常の標本平均はマイナスの偏りを持つので望ましくない.

センサーデータを除いたデータの標本平均で平均を推定する方法もある. この方法は標本の大きさが小さくなり, 推定の精度が悪くなるという欠点を持つ. もともとホテル客室需要は季節性を持ち, 同質と考えられるピックアップの数は多くとれない. したがってセンサーデータを除くことによって標本の大きさが十分でなくなることが多く, この方法は望ましくない.

欠損値のあるデータの分析でよく使われるのが平均代入法（mean imputation）である. この方法は以下のように記述される.

1．センサーされていないピックアップはその値のままにする.

2．センサーされているピックアップは, それ以前のセンサーされていないピックアップの平均によって置き換える. もしこの平均がもとの値（センサーされている値）よりも小さい場合, もとの値を使う.

3．同質な標本になるように適当な標本の大きさを決め, 1で得られたピックアップの標本の平均を求める. この値によって母平均を推定する.

Zeni (2001) が指摘しているように, 上のステップ2でセンサーされていないピックアップは比較的小さい値であることが多いので, その平均でセンサーされているピックアップを置き換えることによって, やはり真の需要増分の平均を過小推定してしまう.

3.2.2　EMアルゴリズム

変数が打ち切られているデータから変数の母平均の望ましい推定値を得るためには, やはり打ち切りのメカニズムを十分情報として活用した推定方法を使う必要がある. そのための一つの方法がEMアルゴリズムである.

第宿泊日の時間における真の需要増分をで表す. は独立で

であると仮定する. ピックアップは以下のように定まる.

【44頁】

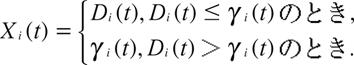
したがっての確率分布のパラメトリック形が既知のときにはEMアルゴリズムを使って最尤推定値を近似することができる. ただし, ピックアップの期間が短い場合, 需要量増分は平均的に小さな値をとり, その場合需要量増分の確率分布は正規分布よりも離散型確率分布が適しているだろう. この場合, 正規分布以外のパラメトリック形を仮定しEMアルゴリズムを実行する必要がある.

Liu, Smith, Orkin and Carey (2002) はピックアップの確率分布の種類（ポワソン分布, ウェイブル分布, 正規分布など）がリード時間, ピックアップの期間, ホテルのサイズなどに依存して変わることを報告している. EMアルゴリズムによって得られたの最尤推定量を（7）式に代入することによっての予測量が得られる.

3.3　その他のモデル

ピックアップ法による予測では, 将来の需要増分の値を予測することが重要である. Liu, Smith, Orkin and Carey (2002) は需要増分を説明するモデルとして, 料金フェンスなどの変数を説明変数とするいつかの回帰モデルを使い需要増分の予測を行っている. 彼らの論文では, 被説明変数（需要増分）がポワソン分布, ウェイブル分布, 正規分布のときの適切な回帰モデルを説明している.

McGill (1995) は複数の料金クラスへの拡張が存在するときに, センサリングの仕組みを明示的に組み入れた回帰モデルを研究した.

４　宿泊室数予測に関する注意

本論文で解説あるいは提案した予測法は, 予測時点以降宿泊価格など客の購買行動に影響を与えるような変数の変更がないことを前提としている. したがって, たとえば予測に基づき価格変更などの販売促進を行えば, 結果的に予測と実績値が大きく乖離することになる.

参考文献

岩崎学（2001）. 不完全データ統計解析, エコノミスト社．

Dempster, A. P., Laird, N. M. and Rubin, D. B. (1977). “Maximum likelihood estimation from incomplete data via the EM algorithm (with discussion).” Journal of the Royal Statistical Society, Series B, 39, 1-38.

Gorin, T. (2000). “Airline revenue management: sell-up and forecasting algorithm”, Master thesis, MIT.

Ingold, A., U. McMahon-Beattie and I. Yeman (ed.) Yield Management : Strategies for the service Sector, second edition. Continuum, London.

Kimes, S. (1989). “The basics of yield management”. Cornell Hotel and Restaurant Administration 【45頁】Quarterly, 30, 14-19.

Liu, P. H., S. Smith, E. B. Orkin and G. Carey. (2002). “Estimating unconstrained hotel demand based on censored booking data.” Journal of Revenue and Pricing Management.

Little, R. J. A. and Rubin, D. B. Statistical Analysis with Missing Data. John Wiley and Sons, New York.

McGill, J. I. (1995). “Censored regression analysis of multiclass passenger demand data subject to joint capacity constraints.” Annals of Operatoins Research, 60, 209-240.

McGill, J. I. and G. J. van Ryzin (1999). “Revenue management : Research overview and prospects.” Transportation Science, 33, 233-256.

Talluri, K. T. and van Ryzin, G. J. (2004). Theory and Practice of Revenue Management. Kluwer, Boston.

Zeni, R. H. (2001). Improved Forecast Accuracy in Revenue Management by Unconstraining Demand Estimates from Censored Data. Ph. D. thesis. Rutgers, State University of New Jersey.

Weatherford, L. R. and S. E. Kimes, (2003). “A comparison of forecasting methods for hotel revenue management”. International Journal of Forecasting, 19, 401-415.