【325頁】
Licensing
of a lower-cost production process to an asymmetric Cournot duopoly
Dimitry
Rtischev１
Abstract
An outside inventor of a new production process seeks
to license it to Cournot duopolists which have unequal ex ante costs. Distinguishing “leading-edge” innovations
(new cost below both firms’ costs) from “catch-up” innovations
(new cost between the two firms’ costs), we
compare the equilibria of two license-selling mechanisms: exclusive license
auction and non-exclusive price-setting.
In contrast to the often-studied case of an innovation that reduces the
cost of any licensee by the same amount, we show that licensing of a new
process may attenuate the ex ante cost asymmetry, allow the inefficient firm to
leapfrog its competitor, and raise the licensee’s net
profits.
1. Introduction
The modern theory of licensing of a cost-reducing
innovation uses game-theoretic models to analyze the interaction among an
inventor and potential licensees who compete in a downstream market. The externalities that the innovation
generates among the downstream competitors makes the upstream trade in
technology a much more complex and subtle affair than trade in a typical market
for procuring inputs. After more
than twenty years of increasingly elaborate models, the theory has examined and
clarified many issues that influence the structure, pricing, and allocation of
licenses, including royalties vs. fixed-fees, auctions vs. price-setting,
inside or outside inventors, and exclusivity. However, the conception of what
constitutes “a cost-reducing innovation” remains elementary. Specifically, most licensing theory
developed so far has focused on identical firms and assumed that a given
cost-reducing technology can bring down unit cost by the same amount at any
firm that licenses it. One goal of
this paper is to propose alternative conceptions of a cost-reducing innovation
that may plausibly arise in a manufacturing industry and engender distinct
strategic consequences. A second
goal is to explore one of those alternatives in detail and compare the results
with previous findings. A third
goal is to demonstrate that doing away with the usual assumption that firms are
identical leads to substantively richer as well as more realistic models of
technology licensing.
We begin in the next section by attempting to ground
the conception of a cost-reducing innovation in specific conditions that may
arise in a typical manufacturing industry, without assuming that firms have
identical costs. This leads us to
interpret the prevalent conception of a cost-reducing innovation as an
innovation 【326頁】that eliminates one step in the production process,
and to identify other plausible kinds of cost-reducing innovations. Focusing on an innovation which
constitutes an entirely new way of producing the downstream good, we proceed to
specify a duopoly model in Section 3 and use it to analyze the sale of a
new-process license via an auction (Section 4) and via price-setting (Section
5). In contrast to step-eliminating
innovations, we show that licensing of a new process can attenuate the ex ante
cost asymmetry and allow the inefficient firm to leapfrog its competitor. We also show that an exclusive-license
auction does not necessarily earn the inventor more revenue than non-exclusive
price-setting.
2. Alternative conceptions of a
cost-reducing innovation
A very general conception of licensing has been put
forth in Katz and Shapiro’s seminal
paper “How to license intellectual property” (1986).
Although they conduct much of their discussion in the specific context
of an inventor licensing an innovation to an oligopoly, they stress that their
model applies to the licensing of any “intangible
property” (IP) that satisfies the following conditions
1. there is only one licensor, and it has access to an
infinite supply of the IP at zero marginal cost (i.e., development costs have been sunk)
2. there are several identical potential licensees,
each of which has use for at most one unit of the IP
3. the profit of the licensee (gross of the license
fee) is higher than the profit of a non-licensee
4. the profit of a non-licensee decreases as more of
its competitors acquire licenses (i.e. ,
by becoming a licensee, a firm imposes a negative externality on a
non-licensee)
Katz and Shapiro stress than these assumptions
describe not only the case of licensing of a cost-reducing technology but also
the licensing of an industry standard or the sale of access to some central
facility. Notably, the authors
abstain from specifying a model of how potential licensees compete in the
downstream market and how obtaining access to the IP affects a firm’s competitive standing. Remaining at a high level of
abstraction, Katz and Shapiro (1986) and Shapiro (1985) derive interesting
general results including:
(i) an inventor obtains more licensing revenue via
auctioning off a limited number of licenses than by setting a price and letting
any interested firm buy, and
(ii) licensing that maximizes inventor’s revenue leaves both licensees and non-licensees with
less net profit than ex ante (i.e.,
the inventor appropriates some of the licensee’s ex ante
profit).
These results have been confirmed and elaborated in
the context of specific models of competition among potential licensees in a
downstream market. Following the
seminal papers of Kamien and Tauman (1984, 1986), most models assume identical
firms with constant marginal cost c>0
engaged in Cournot competition in a market with linear demand. (Kamien, 1992;
Wang, 1998; Sen and Tauman, 2007)
The innovation is defined as a reduction in cost from c to 
, assuming 
. All
firms are assumed identical ex ante and it is also assumed that any firm can
realize the same amount of cost-reduction 
if it puts
the innovation to use.
The case of ex ante cost asymmetries has been largely
ignored. Although the asymmetric
case is much less tractable, there are at least three important reasons why it
deserves attention. First, perfect
cost symmetry is unlikely in any real industry. Second, the assumption of perfect cost
symmetry leads 【327頁】to auction equilibria in which potential
licensees make identical bids, which then requires a random draw to allocate
the license. Some properties of
such equilibria may arise from the tie-breaking rather than from substantive
aspects of downstream competition.
In particular, as our analysis will show, findings (i) and (ii) above
may be violated when firms are not identical. Thirdly, including ex ante cost
asymmetries in a model forces us to clarify the conception of a cost-reducing
innovation by identifying and distinguishing specific ways in which a new
technology may reduce production costs.
This is so because, if firms are not identical in terms of their ex ante
costs, it is likely that they may also differ in the extent to which the
innovation can reduce their costs.
We propose that the following three types of
cost-reducing innovation may plausibly arise in a manufacturing industry and
engender distinct strategic consequences for the allocation and pricing of
licenses.
Step-eliminating innovation.
Ex ante, the unit production cost is 
for firm i.
The production processes used by the firms may differ, but each process
includes a step that is common to all firms. The cost of this common step is 
per
unit. The innovation eliminates
this step, thereby reducing the production cost of a licensee to v. This type of innovation is
congruent to the innovation assumed in most models of the strategic licensing
literature cited above.
New process innovation.
Ex ante, the unit production cost is for firm i.
The innovation is a whole new process to produce the same output good at
a per-unit cost 
. To use
the innovation, a licensee must abandon its previous process and replace it
with the new process. We will take
up this case in detail in the following sections and show that licensing of a
new process innovation is substantively different from licensing a
step-eliminating innovation.
General cost-reducing
innovation. Ex ante, the unit production cost is for firm i.
By adopting the innovation, firm i
can achieve a unit cost 
. Such
firm-specific cost-reductions may arise if a particular input (e.g., electricity) is used by firms in
different amounts and the innovation reduces the cost of procuring that input (e.g., new electricity generator). Since cost-reductions are firm-specific,
the gains to becoming a licensee and the losses from not becoming a licensee
are also firm-specific. An auction
to allocate a limited number of licenses to such an innovation is a special
case of an auction with identity-dependent externalities, a difficult problem
that has received some attention from auction theorists. (see Aseff and Chade, 2008; Das Varma,
2002; Funk, 1996) Applying the
theory of auctions with interdependent valuations to the specific case of
licensing appears to be a promising new direction.
In the remainder of the paper we analyze the licensing
of a new process innovation and compare the results to the case of a
step-eliminating innovation.
3. Model
A Cournot duopoly producing undifferentiated goods
faces inverse demand given by 
, where qi is the quantity produced by firm 
, a>0 is a demand
parameter, and p is the market-clearing
price. We assume that firms have
positive costs and that firm 1 is more efficient.２
To 【328頁】focus attention on non-drastic innovations,
we further assume that the inefficient firm would produce a positive amount
even if the efficient firm were to succeed in reducing its unit cost to
zero. The following condition
incorporates these assumptions about costs:
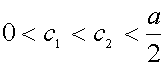(1)
We will use the following notation to denote the
Cournot equilibrium profit of firm i
as a function of its and rival’s unit costs:
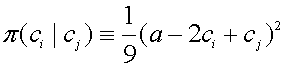
where 
and 
. Ex-ante
profits of the duopolists will be denoted by 
and the ex
ante cost difference by 
.
An independent inventor patents a new production
process that can be used to produce the same goods more efficiently than the
inefficient firm. Specifically, the
new process has a unit cost e
< c2. We
distinguish innovations that are a breakthrough for the industry from
innovations that can help the inefficient firm catch up, as follows.
Definition.
A leading-edge innovation is a
new production process with unit cost e
that satisfies 
.
Definition.
A catch-up innovation is a new
production process with unit cost e
that satisfies 
.
As the following analysis will show, the strategic
consequences of licensing leading-edge and catch-up innovations are quite
distinct.
4. Exclusive licensing via
auction
The inventor may choose to hold an auction to allocate
an exclusive zero-royalty license to the innovation.３ Each firm’s bid in the
auction represents a per-period fixed fee the firm is willing to pay to become
the exclusive licensee. The auction
is conducted as a sealed-bid second-price auction. Let Wi represent the profit of firm i if it wins at auction, gross of the
license fee it will have to pay.
Let Li represent
the profit of firm i if it loses the
auction. Since the auction is
second-price, it is optimal for each firm to enter a bid equal to its
willingness-to-pay. The firms thus
bid 
, the highest bidder becomes the licensee, and
thereafter pays a license fee 
per
period. We can decompose the
willingness to pay for the license into “use value” and “loss-prevention
value.”
The use value of the license to firm i
is 
, since this is how much it can gain from using the
new technology. The loss-【329頁】prevention value
is 
, which represents the loss a firm will suffer if its
rival gets the license.
4. 1 Exclusive licensing of a catch-up
innovation
The efficient firm has zero use value for a catch-up
innovation, since if it obtains the license, it would be most profitable to
shelve the new technology and keep producing with the old process. However, the efficient firm has
loss-prevention value for a catch-up innovation, because by obtaining a license
it can prevent its rival from becoming more efficient. Specifically, the gross payoffs to the
efficient firm from winning or losing the auction are:
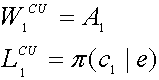
The inefficient firm has zero loss-prevention value
but positive use value for a catch-up innovation, since the inefficient firm
loses nothing if the efficient firm licenses the innovation and then shelves
it. Specifically, after the auction
the inefficient firm stands to earn one of the following gross profit levels:
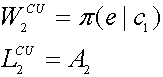
In the auction, the firms bid 
.
Regardless of which firm wins the license, the inefficient firm will not
suffer a loss in net profit but the efficient firm will. The next proposition makes this precise.
Proposition 1. Allocation of an exclusive license to a
catch-up innovation via an auction weakly increases the net profit of the
inefficient firm and strictly decreases the net profit of the efficient firm.
Proof.
The inefficient firm can retain its ex ante profit by bidding zero in
the auction, letting the efficient firm win the license and shelve the new
process. Thus, if the inefficient
firm chooses to make a positive bid, it must be for the purpose of obtaining a
higher net profit in the case of winning the auction. If the efficient firm wins the license,
it shelves the technology. Its
profit from production remains unchanged but net profit falls by the amount of
the license fee. ■
Which firm wins the license leads to different
consequences not only for the firms’ profits but
also for consumer surplus and the source of inventor’s compensation.
If the inefficient firm gets the license, the inventor appropriates part
of the new profit the innovation brings to the licensee, but not any of its ex
ante profit. The lower cost enjoyed
by the licensee will lead to more output, lower price, greater consumer
surplus, higher net profit for the inefficient firm, but lower profit for the
efficient firm. Thus, by licensing
a catch-up innovation to the inefficient firm, the inventor ends up hurting the
efficient firm indirectly, via competition in the output market, and ends up
helping its direct client - the licensee - as well as downstream
consumers. However, if the
efficient firm wins the license, there will be no change in 【330頁】quantities,
prices, consumer surplus, or the inefficient firm’s
profit. The inventor will have
simply appropriated part of its client’s ex ante
profit − a pure transfer of an incumbent’s rent with no efficiency consequences.
Which firm will win the license to a catch-up
innovation depends on the ex ante cost asymmetry and the size of the
innovation. The next three
propositions specify the relevant conditions.
Proposition 2.
If the ex ante cost asymmetry is larger than 
then any catch-up
innovation will be licensed by the inefficient firm.
Proposition 3. If the ex ante cost asymmetry is smaller
than 
then any
catch-up innovation will be licensed by the efficient firm.
Proposition 4. If the ex ante cost asymmetry falls in
the range 
then there
exists a critical size of a catch-up innovation 
such that
any more significant catch-up innovation 
will be
licensed by the inefficient firm and any less significant catch-up innovation 
will be
licensed by the efficient firm. The
critical size of a catch-up innovation is 
. The
bigger (smaller) the ex ante cost asymmetry, the broader (narrower) the range
of catch-up innovations licensed by the efficient firm.
Proof. The bids of the efficient and
inefficient firms for an exclusive license to a catch-up innovation are,
respectively, 
and 
. From
this it follows that 
if and
only if 
. Imposing
the restrictions 
and 
, and using the definition of ex ante cost asymmetry 
leads to
Propositions 2 through 4. ■
The overall picture that emerges from these results is
that a catch-up innovation will end up being put to use by the inefficient firm
only when the ex ante cost asymmetry is large enough and if the innovation
promises a large enough cost reduction.
Thus, only significant catch-up innovations in significantly asymmetric
duopolies can be expected to end up in the hands of the inefficient firm and
thereby reduce the cost asymmetry and increase consumer surplus. Conversely, a sufficiently small ex ante
cost asymmetry will be perpetuated in spite of any catch-up innovations offered
for licensing by outside inventors.
Such inventions will be kept out of use by preemptive licensing by the
efficient firm. This implies that
it is possible for a slightly more efficient firm to be driven to progressively
lower profit levels by a series of outside inventors auctioning off catch-up
innovations. Considered in
isolation, each such auction for a catch-up innovation makes it rational for
the efficient firm to outbid the inefficient firm and then shelve the
innovation. However, by
accumulating such licenses the efficient firm will progressively pay out more
of its gross profit to the inventors, eventually ending up with zero net
profit.４ We caution that the rationality of such
preemptive licensing may be questioned in a model that allows firms to
anticipate 【331頁】future innovations.
4.2 Exclusive licensing of a leading-edge
innovation
A leading-edge innovation has both use value and
loss-prevention value for both firms.
Specifically, the gross payoffs to firm i from winning or losing the auction, respectively, are:
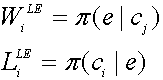
For each firm, winning a license auction increases
gross profit 
whereas
losing decreases it (
).
This win-or-lose situation is structurally similar to the case of a
step-eliminating innovation that is the focus of most strategic licensing
models cited earlier. However,
because the licensing of a new process to an asymmetric duopoly engenders
different amounts of cost-savings for the two firms, there are equilibria
different from those identified in the literature on step-eliminating
innovations. Specifically, whereas
in the case of a step-eliminating innovation the efficient firm always outbids
the inefficient firm and thereby increases the cost asymmetry via licensing,
the opposite outcome is possible in the case of a leading-edge new process
innovation. The next three
propositions make this precise.
Proposition 5. If the ex ante cost asymmetry is larger
than then any
leading-edge innovation will be licensed by the efficient firm.
Proposition 6.
If the ex ante cost asymmetry is smaller than 
then any
leading-edge innovation will be licensed by the inefficient firm.
Proposition 7. If the ex ante cost asymmetry falls in
the range 
then there
exists a critical size of a leading-edge innovation 
such that
any more significant innovation 
will be
licensed by the efficient firm and any less significant leading-edge innovation
will be
licensed by the inefficient firm.
The critical size of a leading-edge innovation is 
. The
bigger the sum of the ex ante costs, the larger the range of leading-edge
innovations licensed by the efficient firm.
Proof. Firm
i bids for an
exclusive license to a leading-edge innovation 
in the
amount of 
. From
this it follows that if and
only if 
. Imposing
the restrictions 
and 
, and using the definition of ex ante cost asymmetry leads to
Propositions 5 through 7. ■
The overall picture that emerges from these results is
that a sufficiently large ex ante cost gap will be widened by a leading-edge
innovation. However, if the initial
cost asymmetry is not too large and the leading-edge innovation is not too
significant, then the inefficient firm will license the innovation and leapfrog
the efficient firm. Such
leapfrogging is not possible when licensing a step-eliminating innovation,【332頁】 as the next
proposition shows.
Proposition 8. Any step-eliminating innovation 
is
licensed by the efficient firm.
Proof. Firm i
bids for an exclusive license to the step-eliminating innovation in the amount
of 
. From
this it follows that 
, which implies firm 1 wins the auction. ■
In particular, if a step-eliminating innovation
satisfies 
, then potentially the inefficient firm could leapfrog
its competitor if only it could obtain the exclusive license. However, according to Proposition 8, the
efficient firm will outbid the inefficient firm in the auction and thereby
widen the cost asymmetry.
5. Non-exclusive licensing of a new
production process via price-setting
Instead of holding an auction to allocate an exclusive
license, the inventor can set a price and offer a non-exclusive license to any
firm willing to pay the price. In
this section, we consider the allocation of licenses and inventor revenue under
such price-setting, and identify conditions under which the inventor prefers
price-setting to auctioning.
5.1 Licensing of a catch-up
innovation via price-setting
An inventor choosing how to sell license(s) to a
catch-up innovation would choose to hold an auction only for those innovations
that would be won and shelved by the efficient firm. If the auction would lead to licensing
by the inefficient firm, the inventor could earn more by non-exclusive
price-setting. The next proposition
makes this precise.
Proposition 9. If the inventor offers non-exclusive
licenses to a catch-up innovation, then (i) the efficient firm will not buy a
license at any positive price, and (ii) the inventor will earn higher licensing
fees than via exclusive auctioning if the innovation satisfies conditions in
Propositions 2 and 4 under which the inefficient firm wins the auction.
Proof.
(i) The efficient firm would not pay for a
non-exclusive license since the use value is zero and loss-prevention value
cannot be realized without exclusivity.
(ii) If an auction for an exclusive license is won by
the inefficient firm, then the firms’ bids must
have satisfied 
and the
license fee must be the smaller bid 
. If
instead of holding an auction, the inventor were to set the price slightly
below 
, then the inefficient firm would have bought the
license, since doing so would raise its profit. Since 
, the inventor would have earned more revenue. ■
Thus, it makes sense for the inventor to hold an
exclusive auction for a catch-up innovation only if the loss-prevention value
for the efficient firm exceeds the use value for the inefficient firm. Otherwise, 【333頁】price-setting is a more profitable way for
the inventor to sell the license to the inefficient firm. Even though price-setting potentially
makes the innovation available to both firms on a non-exclusive basis, in
effect the outcome is a single license to the efficient firm.
5.2 Licensing of a leading-edge
innovation via price-setting
If both firms obtain a license to a leading-edge
innovation, then each firm will earn a gross profit which we will denote by 
. Figure 1
shows the firms’ payoff matrix in the price-setting licensing
game in which the inventor first announces a license fee F per period and then each firm decides whether to buy a license or
not. As the following propositions
establish, there are two candidate prices that the inventor must choose from
when setting a non-exclusive license fee to a leading-edge innovation: either 
or 
.
Lemma 1. For any leading-edge innovation 
and any
cost and demand parameters satisfying (1), Cournot profits gross of the license
fee satisfy all of the following inequalities:
(i) 
(ii) 
(iii) 
(iv) 
Proof. Inequalities (i), (ii) and (iii) follow
from the definitions of the Cournot profit functions. To prove (iv), we note that the equation
reduces to
, which has no real roots in e. Thus 
as a
function of e is a parabola with no
zero-crossings. Therefore, for all e, either or 
. When e = c1, ; therefore this must hold for all e. ■
Proposition 10.
The highest price an inventor can set such that both firms will buy a
license to a leading-edge innovation is . Both
firms will suffer a decrease in net profit as a result of buying a license at
this price.
【334頁】Proof.
From the payoff matrix in Figure 1, it can be seen that (Buy, Buy) is a
Nash equilibrium of the price-setting licensing game if and only if 
and 
.
According to Lemma 1(i), 
.
Therefore, is the
binding upper limit on the license fee. After the firms purchase licenses
at this price, each firm’s net profit
will be 
, which is less than A1 and A2 by Lemma
1(i). ■
Proposition 11.
The highest price an inventor can set such that exactly one firm will
buy a license to a leading-edge innovation is . This
price will induce only the inefficient firm to become a licensee. The licensee’s net profit
will be the same as ex ante; non-licensee’s profit will
be lower than ex ante.
Proof. From the payoff matrix in Figure 1, it
can be seen that (Don’t buy, Buy) is a Nash equilibrium of the
price-setting licensing game if and only if 
and 
. Such a
fee F exists by Lemma 1(iv). Next, we need to confirm that the
inventor cannot obtain a higher license fee in the (Buy, Don’t buy) equilibrium. (Buy, Don’t buy) is a
Nash equilibrium if and only if 
and 
.
According to Lemma 1(iii), the upper bound on F in this equilibrium is below that of the (Don’t buy, Buy) equilibrium. Finally, ex post profits in the (Don’t buy, Buy) equilibrium with the price are 
for firm 1
and 
for firm
2. ■
The next proposition identifies conditions under which
the inventor prefers to set the license fee aiming to license both firms, and
conditions under which the inventor prefers to set the fee so as to license
only the inefficient firm.
Proposition 12.
An inventor who uses price-setting to sell licenses to a leading-edge innovation
maximizes licensing revenue by setting the fee to , and thereby licensing both firms, if 
and 
.
Otherwise (i.e., if 
, or and 
), the inventor maximizes licensing revenue by setting
the fee to and
thereby licensing only the inefficient firm.
Proof. The inventor can set the price to
attract either one or both firms.
Propositions 10 and 11 establish the highest price possible for each
case. Inventor’s maximum revenue from licensing both firms is 
, which exceeds the maximum revenue from licensing one
firm 
iff 
. This inequality
reduces to 
. Applying
assumption (1) constrains e to the
range 
. ■
Finally, we consider conditions under which an
inventor of a leading-edge innovation earns more via exclusive auctioning than
via non-exclusive price-setting. As
the next proposition establishes, if price-setting results in licensing only a
single firm, the inventor can earn more revenue by instead holding an auction
for an exclusive license.
Proposition 13.
If licensing a leading-edge innovation via price-setting would result in
licensing only one firm, the inventor can earn more revenue by instead
auctioning off an exclusive license.
【335頁】
Proof. If or if and , then, according to Proposition 12, the
profit-maximizing price is 
, only the inefficient firm buys, and the licensing
revenue is F2. An auction for an exclusive license
would yield 
in
licensing revenue, which exceeds F2 according to Lemma 1(i). ■
As can be easily verified with a numerical
counter-example, the converse of Proposition 13 does not hold. Thus, in cases when price-setting would
result in both firms buying a license, the inventor may or may not find it more
profitable to instead auction off an exclusive license. Unlike in models with identical firms
licensing a step-eliminating innovation, the inventor in our model does not
necessarily earn more via exclusive-license auctioning than via non-exclusive
price-setting.
6. Conclusion
We began by inquiring into how the usual theoretical
definition of a cost-reducing innovation may be interpreted in the context of a
typical manufacturing industry, and whether there are other plausible kinds of
cost-reducing innovations. We have
outlined a brief typology of cost-reducing innovations that distinguishes
step-eliminating, new-process, and general cost-reducing innovations. We then focused on the licensing
of a new process innovation, keeping track of its two sub-types: leading-edge
and catch-up innovations. The
licensing equilibria that we have derived are substantively different from
those in previous studies focused on the case of symmetric firms licensing a
step-eliminating innovation. We
have shown that when firms with different ex ante costs engage in a game to
allocate a license to a new process via auction or price-setting, outcomes that
have been ruled out in many strategic licensing models become possible. In particular, the relatively inefficient
firm may catch-up to and even leapfrog its rival, price-setting without
quantity restrictions may yield higher licensing revenue to the inventor than
auctioning off a restricted number of licenses, and the licensee does not
necessarily end up with less net profit than ex ante.
References
Aseff, J., Chade H., 2008. An optimal auction with
identity-dependent externalities. RAND Journal of Economics 39:3, 731-746
Das Varma, G., 2002. Standard auctions with
identity-dependent externalities. RAND Journal of Economics 33:4, 689-708
Funk, P. 1996. Auctions with interdependent
valuations. International Journal of Game Theory 25, 51-64
Kamien, M., 1992. Patent Licensing. In: Aumann, R.,
Sergiu, H. (Eds.), Handbook of Game Theory with Economic Applications, Vol. 1,
Kamien, M., Tauman Y., 1984. The private value of a
patent: a game theoretic analysis. Journal of Economics (Suppl) 4, 93-118
Kamien, M., Tauman, Y., 1986. Fees versus royalties
and the private value of a patent. Quarterly Journal of Economics 101:3,
471-492
【336頁】Katz, M., Shapiro, C., 1986. How to license
intangible property. Quarterly Journal of Economics 101:3, 567-589
Sen, D., Tauman, Y., 2007. General licensing schemes
for a cost-reducing innovation. Games and Economic Behavior 59:1, 163-186
Shapiro, C., 1985. Patent licensing and R & D
rivalry. American Economic Review 75:2, 25-30
Wang, X., 1998. Fee versus royalty licensing in a
Cournot duopoly model. Economics Letters 60, 55-62