�y293�Łz
�o�c�w�Ȋw���̐��w������Ɋւ���I�D����
���c�@�R������
�v�|
�{�_���ł́C�o�c�w�Ȃɂ����鐔�w���Ƃ����P���邽�߁C�w�����l���闝�z�̐��w������Ɋւ���I�D�͂���B��@�́C�o�c�w�Ȃ̐��w�֘A�̎��Ƃ̎�u�҂�ΏۂɁC�A���P�[�g�������s���C�R���W���C���g���͂��s�����B���ʂƂ��āC�w���́C�u����������Ȃ��Ƃ��̎�����@�v�C���Ɂu�S�������ł��Ȃ��Ƃ��̎w���@�v���ŏd�v�����Ă��邱�Ƃ����炩�ɂȂ����B�����u����������Ȃ����̎�����@�v�Ɋւ��ẮC�u���ƒ��ɐ搶�Ɏ���v�̌��p�l�������C�u�@���ɂ��w���v�f�X�N�v�͒Ⴉ�����B�����u�S�������ł��Ȃ����̎w���@�v�Ɋւ��ẮC�u�w��e�L�X�g�C�h�����v�̌��p�l�������C�ue-Learning�v�͒Ⴉ�����B���̒������C�ŏd�v�����́u����������Ȃ��Ƃ��̎�����@�v�ł��邱�Ƃ��������ꂽ�B
�P�D�͂��߂�
�{�_���ł́C�o�c�w�Ȃɂ����鐔�w���Ƃ����P���邽�߁C�w�����l���闝�z�̐��w������Ɋւ���I�D�͂���B
�ߔN�C�����̑�w�ɂ����Ċw���ɂ����ƕ]�����s���Ă���C�{�w�ɂ����Ă�2006�N�x�����{����Ă������B���ƕ]���̖ړI�͂��̌��ʂ����ɁC���Ɖ��P���s���邱�Ƃł��邪�C�A���P�[�g�͌��ݍs���Ă�����Ƃɑ���]������ړI�Ƃ���B�{�����̖ړI�͂���Ƃ͈قȂ�C�w���ɂƂ��čD�܂������z�̐��w������m�����邱�Ƃł���B�������ڂɂ́C���{������Ȃ��̂��܂܂�Ă��邪�C����ł́C���̂悤�Ȑ���̖�������z�肵�ĉ��Ă�������B
�{�����́C��w�S�̂ōs�����ƕ]���̃A���P�[�g�����Ƃ͕ʂɁC�M�҂��S�����Ă���ȉ��̍u�`�̎�u�҂̋��͂�2008�N6������7���ɂ����Ď��{�����B
�� �o�c���w1�i�o�c�w�Ȃ�1�N������j
�� �o�c���剉�K�i1�N���̂݁j
�� ���}�l�W�����g�i�z���N��3�N�C4�N�j
�� �o�c�w����u�`�i�o�c���w��b1�j�i�z���N��3�N�C4�N�C��w�@���j
���͂ɂ̓R���W���C���g���͂𗘗p�����B�R���W���C���g���͂̓}�[�P�e�B���O�E���T�[�`�̕���ŐV���i�R���Z�v�g���J������ۂɗ��p����Ă������͎�@�ł��邪�C�����ł͋�����y294�Łz�����̕���ł����p����Ă���[1�C2]�C[3]�B
�R���W���C���g���͖@�ł́C���i�̎d�l���L�q����ϐ����ƌĂсC�����Ƒ����̎�肤��l�𐅏��ƌĂ�ł���B�����̑g�������ЂƂ̐��i�R���Z�v�g�ɑΉ�����B�����ĉ҂ɕ����̃R���Z�v�g����C�R���Z�v�g�Ԃ̑I�D���ʂ����߂Ă��炤�B�팱�҂������̃R���Z�v�g�ɑI�D���ʂ�^���邱�ƂŁC�팱�Ҏ��g���C�Â��Ă��Ȃ������I�D�ɑ��鑮���̌��p���ipart worth
function�j�������\�ƂȂ�[4]�B
�{�_���ł́C���w������Ɋւ���w���I�D�Ɋւ��R���W���C���g���͂��s�Ȃ��C���̌��ʂ����B���߂ł́C���̓��f���C�܂�ݒ肵�������Ƃ��̐����ɂ��Đ�������B��3�߂ł́C�R���W���C���g���͂̂��߂̃A���P�[�g�����[�ɂ��Đ�������B��4�߂́C���͂̌��ʂł���B��5�߂͂܂Ƃ߂Ƃ���B
�Q�D���̓��f��
����̕��͂Őݒ肵����������ё����������������B�A���P�[�g�ɍۂ��C�������鑮���������߂���Ɖ҂̊w���͔�r������ɂȂ�C�̐M������������Ƃ�����肪��������B�����ŁC�ȉ���5�����Ƃ����B�e������3���邢��2�̐��������B
�P�D����������Ȃ��Ƃ��̎�����@
��e-Learning�V�X�e����FAQ��T���B
�i�r�f�I���ނʼnB24���ԉj
���w���v�f�X�N�ʼn@���������Ă����B
�i24���ԑΉ��ł͂Ȃ��C���Ԃ͌��肳���j
�����ƒ��ɐ搶�Ɏ��₵�ĉ�������B
�Q�D�S�������ł��Ȃ��Ƃ��Ɏw�������߂���@
��e-Learning�V�X�e���� �u�`�̓��������B
�i�r�f�I���ނŎ����B24���ԉj
���w��e�L�X�g�Ǝw��h����������C����ɂ����Ă��悢�悤�ɂȂ��Ă���B
���搶�Ɏ����ɂ����������@���ʂɎw�����Ă��炢�����B
�i�Z�����ԂƂȂ邱�Ƃ͎d�����Ȃ��j
�R�D���Ɠ��e����
�������������Ԃ��ŏ��ɂ���C���Ƃ��������B
�����������C���̒��Ő搶�����������B
�S�D���[�N�h�����̎��Ԕz��
�����ƒ��Ƀ��[�N�h�����̎��Ԃ𑝂₵�Ăق����B
�����Ǝ��Ԃɂ̓h�����͏��Ȃ��C�h��ɂ��Ăق����B
�T�D�\�͕ʕҐ��N���X�̐���
���\�͕ʃN���X���悢
����������̂͌���
��L�̑����͂�������M�Ҏ��g�C�w�����ǂ̂悤�ȉ�����̂��\�z�����Ȃ��̂ŁC�����������Ɗ��������⍀�ڂł���B�����ʼn��肵������`�Ԃɂ��āC�������̐����ɂ��Đ������K�v�Ǝv����̂Ő�������B
�y295�Łz�܂��C�����u����������Ȃ��Ƃ��̎�����@�v�ƁC�����u�S�������ł��Ȃ��Ƃ��Ɏw�������߂���@�v�̈Ⴂ���������B���w�Ƃ����ۖڂ̏ꍇ�C�e�l��
�o�b�N�O���E���h�����̉ۖڂɔ�ׁC�傫���قȂ�B���Z���w�ŗ��C���Ă����Ȗڂ̈Ⴂ�C��w�ȖڂƂ��Đ��w��I���������ۂ��̈Ⴂ�C�Ȃǂɂ��C�K�n�x�̌l�����傫���B���̂��߁C���Ƃ��S�������ł��Ȃ��C�Ƃ������p�ɂɋN����₷���B���̂悤�ȑS��������Ȃ��ɑ���w�����@�ƁC�������₵�ĕ����Ε�����Ƃ����ł̎w�����@�͎��I�ɈقȂ���̂��K�v�ł���C�ƕM�҂͍l�����B
�����u����������Ȃ��Ƃ��̎�����@�v�̐����ɂ��Đ�������B�܂�e-Learning�V�X�e���Ƃ��đz�肵�Ă�����̂́C24���ԁC�C���^�[�l�b�g��ʂ��ăA�N�Z�X�\�Ȃ��̂ł���B����̃r�f�I�f�[�^�x�[�X��z�肵�Ă���B����Ƃ́C���t���u�`���Ă���l�q�C����уv���[���e�[�V������ʂ̓���C�R���s���[�^��ʂ̓���Ȃǂł���B���݂̋Z�p�ł́C����ɑ��Ĕ������I�ɃC���f�b�N�X�L�[�Ȃǂ�t�����邱�Ƃ��\�ł���[5�C6]�B�����̋Z�p�����邱�Ƃɂ��C�����͍u�`�̓���ɑ��ăL�[���[�h�������s�����Ƃ��\�ƂȂ�B�Ⴆ�C�u�����̃`�F�C�����[���v�Ƃ����L�[���[�h�Ō������s�����ƂŁC�����̃`�F�C�����[�����������r�f�I���ނ��q�b�g���C�R���s���[�^��ʏ�ł��̃r�f�I���ނ������\�ƂȂ�B
�A���P�[�g�ɍۂ��ẮC���̂悤�ȏ����I�ȋZ�p�̉\���܂ł��܂߂āC�����ue-Learning�V�X�e���v�̐������s�����B
���ɐ����u�w���v�f�X�N�v�ɂ��Đ�������B�w���v�f�X�N�Ƃ́C�R���s���[�^�ł͂Ȃ��C���g�̐l�Ԃ��Θb�I�ɑ�������Ă���鎿����@�ł���B��w�����ł͂Ȃ��C���w�ɏK�n������w�@��������ɓ����Ă����悤�ȏ��z�肵���B�`���[�^�[���x�Ƃ��Ă�Ă�������ł���B��������Ƀw���v�f�X�N�ƌĂԁB�Ⴆ�Ίw�����ۑ���Ƃł���Ă��ĕ�����Ȃ��Ƃ��ł��C�w���v�f�X�N�ɍs���C�@��������������`���Ă����B
�{�w�Ȃ̐��w����ɁC��L�̂悤�ȃr�f�I�f�[�^�x�[�X�Ɋ�Â�e-Learning�V�X�e�����C��������Ă���킯�ł͂Ȃ��B�����܂ł����z�̊��ł���B�܂��C�w���v�f�X�N�����݂͓�������Ă��Ȃ��B�w���v�f�X�N�ɂ��ẮC�o�ϊw���Ƃ���2009�N�x�����{����v�悪����B
���̓��f�����C2�Ԗڂ̑����u�S�������ł��Ȃ��Ƃ��Ɏw�������߂���@�v�Ƃ́C�w�����S���u�`�̓��e�𗝉��ł����C�r���ɂ��ꂽ��Ԃł���Ƃ��̎x�����@�Ɋւ��鑮���ł���B�܂�e-Learning�ł��邪�C��L��e-Learning�̊��p�@�ƈႤ�Ƃ���́C������Ȃ��ӏ����w�ǑS�Ăł��邱�Ƃł���B��L�̂悤�ɏ��Ȃ���C�s���|�C���g�̏��Ȃ��ʂ̐����ʼn����ł���B�������C�S�������ł��Ȃ��ł́C�u�`�̃r�f�I�����߂���̌n�Â��Č��Ă����K�v������B�{���f���쐬�ɂ������ẮC�E�ړI�ɉ����āC���ރR���e���c���Ⴄ�����z�肵�Ă���B�܂��C����͉҂̊w���ɂ��������Ă���B
2�Ԗڂ̐����u�w��e�L�X�g�E�h�����v�ɂ��Đ�������B����́u�w�K�̎w�j�����������̍����e�L�X�g��������C�����̃y�[�X�Ŋw�K�\�ƂȂ�C���ʂƂ��ču�`�������ł���悤�ɂȂ�ł��낤�v�Ƃ��������̂��ƁC�ݒ肵�������ł���B
���f���쐬���ɂ����āC�S�������ł��Ȃ��Ŋw���͉����D�܂����Ǝv�����́C���t�Ƃ��Đ���Ƃ��m�肽���_�ł������B�w�����ϋɓI�ɓƊw�Ŋw�ڂ��Ƃ���^�C�v�ł���Ce-Learning����юw��e�L�X�g�̌��p�l�������Ȃ�ł��낤�ƁC�M�҂͗\�������B��ʓI�Ɍ��āC�I�ԓx�ł���C���C���t�ɕ����ɗ���ł��낤�B���������ʁC�w�����I�ł����Ă��C�S��������Ȃ����ł́C���t�Ɏ�������邱�Ǝ��̂�����ł���C���ׂ��傫���̂ŁC�u�y296�Łz�搶�Ɏ����ɂ����������@���ʂɎw�����Ă��炢�����v�͑I������ɂ����̂ł͂Ȃ����Ƃ��\�������B���͌��ʂ́C��q����悤�ɁC�u�w��e�L�X�g�C�h�����v�̌��p�l�������C���Łu�搶�Ɍʂɑ��k�v�C�����āue-Learning�v�͒Ⴉ�����B
�����u���Ɠ��e�v�́C�n�߂Ƀh�������������Ă������������ق����C�������e�Ղł��邩�ۂ���₤�����ł���B���i�擾�̂��߂̗\���Z�Ȃǂł́C�����������Ƃ��d�����C�܂�������������Ă���C�����ɓ��邱�Ƃ������Ǝv����B�o�c���w����̏ꍇ�C�]������̑�w�u�`�̂悤�ɑ̌n�Â��Ă�������ƕ������u�`����`�Ԃ��]�܂�邩�C���邢�́C�S�[���ƂȂ�����ɉ������Čォ�����������ق����]�܂��̂��C�͂��邽�߂ɐ݂��������ł���B�O�҂̏ꍇ�ł��C���������Ƃ������Ԃ͏\���܂ށC�Ɖ��肵�Ă���B
�����u���[�N�h�����̎��Ԕz���v�́C�h��̗L���ɂ��Ă̐ݖ�ł���B�����������邱�Ƃ����[�N�h�����ƌĂ�ł���B���[�N�h�����͎��ƒ��ɂ����ق����悢���C�h��ɂ����ق����悢���C�Ƃ������ł���B
�����u�\�͕ʕҐ��N���X�̐���v�́C�����ʂ�C�\�͕ʂɃN���X�����������ق����]�܂������ۂ���₤�Ă���B�ߋ��̊w���ւ̃A���P�[�g�̌��ʂ�����ƁC�u���Z�Ő��w1�������C���Ă��Ȃ������̂ŁC��������̂�����B���������O�i�K�̍u�`��ʓr����Ăق����v�Ƃ����ӌ����������B����̓N���X�ʕҐ��^���̑�\�I�ӌ��ƌ����悤�B
���āC�R���W���C���g���͂ł̓��f���ɑ��āC�e�����݂͌��ɓƗ��łȂ��Ă͂����Ȃ��C�Ƃ���������[7]�B�{���f���ɂ����ẮC�����ԂɊ֘A�͂Ȃ��C�݂��ɓƗ��ł���B�h��C�h�����Ɋւ��鑮���Ƃ��āC�u���Ɠ��e�����v�Ɓu���[�N�h�����̎��Ԕz���v������B�u���[�N�h�����̎��Ԕz���v�͏h��̗ʂ̖��ł���C�u���Ɠ��e���ԁv�ł͂��̗ʂ̂�����ɂ�����炸�C���ʂ̖������Ɠ��ʼn����Ƃ��̏����ɒ��ڂ��Ă���̂ł��邩��C�֘A�͖����B����đ����݂͌��ɓƗ��ł���B
�{�߂̍Ō�ɁC���f������͂����������ɂ��ďq�ׂ�B�R���W���C���g���͂̐�������C�������͈�萔�ɉ�����K�v������B���̂��߂Ɉȉ��̑����̓��f������폜�����B
�E�N���X�̐l��
�E���ށF�i1�j�����S�C�i2�j�v���[���e�[�V�������S
�܂��C�N���X�̋K�͂ł��邪�C�w���ɕ����܂ł��Ȃ����l�����]�܂��Ǝv��������ł���B�A���P�[�g�ł́C50�l�ȏ�́C�����闧���u�`��z�肵�Ď�����s���Ă���B�A���P�[�g�����{�����N���X�̂����C�����u�`�͌o�c���w1�݂̂ŁC����3�N���X��10�l���x�̏��l���N���X�ŁC��l1��̃R���s���[�^�������IT���[���ōs���Ă���B��҂�3�N���X�̎�u�҂��w�ǂ�1�N���̍ہC�o�c���w1�𗚏C���Ă���C���̌o�c���w1���w�ȓ��̌o�c���w�̊�b�I�Ȗڂƌ�����̂ŁC�ÖقƂ��āC�w�������ɃC���[�W���鐔�w�̎��ƂƂ́u�o�c���w1�v�ł���ƍl������B
�����u���ށv�́C���삪�R���s���[�^�E���e���V�[�̎��Ƃ̃R���W���C���g���͂̍ہC�g���Ă��鑮���ł���[3]�B���̌��ʂƂ��ẮC�v���[���e�[�V�����̕������ɔ�r���Č��p�l�����������C�Ƃ���B�M�҂��R���s���[�^�E���e���V�[���u�`����ۂ́C���ނ̓v���[���e�[�V�����Ƃ��Ă���B�������C���w�ƃR���s���[�^�E���e���V�[�̎��Ƃ́C��������e�̎��ɈႢ������B���w�ł́C�o�c���w�̖��������Ȃ�����C��㈓I���_�Ȃǂ̃V�X�e�}�e�B�b�N�ȍl�����������邱�Ƃ��d������B����Ď��̕ό`�Ȃǂ͔����g���C���t���l���C�������y297�Łz���Ă���l�q�������邱�Ƃ��d�v�ł���C�ƍl����B����āC�w���͗��҂̓K�ȕ��p��]�ނł��낤�Ɛ��@���āC���̑��������f������͂������B
�R�D�R���W���C���g���͂̕��@
��2�߂ŋL�q����5�̑�������\������镪�̓��f���ɑ��ăR���W���C���g���͂��s���B
���������̑g�������X�̃Z�b�g���R���Z�v�g�ƌĂԂ��C�������₻�̐������������ƃR���Z�v�g�̐���������B�R���Z�v�g���������Ɖ҂̕��S�����債�C���ʂ̐M�������Ⴍ�Ȃ�̂ŁC�R���Z�v�g���͑������Ă͂����Ȃ��B���̂��߂ɒ��s���v���p���ăR���Z�v�g�̐������炷�B����̃��f���ł́C���s���v����s�������ʁC�R���Z�v�g����16�Ɍ��炷���Ƃ��ł����B
����16�̃R���Z�v�g��1�������J�[�h�ɂ��āC�҂��R���Z�v�g�J�[�h�S�̂ɖ]�܂������ɏ��ʂ�^����C�Ƃ��������^�̎�����@��������B�{���̓R���Z�v�g�J�[�h����肻����҂ɓn���Ĕ�r�������s���Ă��炤�ׂ��ł��邪�C���{�̗e�Ր����l�����C�܂����{���Ԃ̒Z�k�̂��߁CA4�T�C�Y�̗p����16�̃R���Z�v�g�����X�g�A�b�v���C��r�������Ă�������i�}1�Q�Ɓj�B

�A���P�[�g�ɐ旧���C���̓��f���̐������҂̊w���ɑ��ĕM�Ҏ��g�ōs�����B�z�肵�Ă���e-Learning�V�X�e���̗p�@�Ȃǂɂ��ẮC���ɏڂ������������B
�u����������Ȃ��ꍇ�̖]�܂�������̌`�Ԃ́H�v�u�S�������ł��Ȃ��ꍇ�̖]�܂����w���̌`�Ԃ́H�v�Ƃ����悤�Ȏ���ɑ��āC�A���P�[�g�p���̃R���Z�v�g���C���[�W���邱�Ƃ͗e�y298�Łz�Ղł͂Ȃ��B�҂́C�ЂƂ̃R���Z�v�g���C���[�W���邽�߂����ł��C�����������ǂ̂悤�ɐ��w���w�K���Ă���̂��C�����Ď��₳��Ă���R���Z�v�g�ł͂ǂ̂悤�Ȋ��ɕς��̂����C���ԓI�y�ы�ԓI�Ɋe��̏�ʂ�z�����Ȃ���l����K�v������B����ĉɍۂ��āC���Ȃ�W���͂�v����B
�M�҂�����ꍇ�ł��C�R���Z�v�g����16�����E�Ɗ������B16�̔�r�����͂��Ȃ�̃��[�L���O��������K�v�Ƃ���B���̕��ɘa�̂��߁C�D�������̃}�[�N����ݒ肵���i�}�P�Q�Ɓj�B�D���C�����ŁC�n�߂�2�̃O���[�v�ɃR���Z�v�g�ނ��邱�ƂŁC��x�ɔ�r��������R���Z�v�g������8�Ɍ��炷���Ƃ��ł��邩��ł���B
����78�ł��邪�C���L�����̗��R�Ŗ����ȉ����������߁C���͂ɗp�����f�[�^����57�ł���B�A���P�[�g�����{����4�̃N���X�̗��C�҂ɂ́C���Ȃ�d�������邪�C�͈�l���Ƃ��ďd�����������B
�S�D���͌��ʂƍl�@
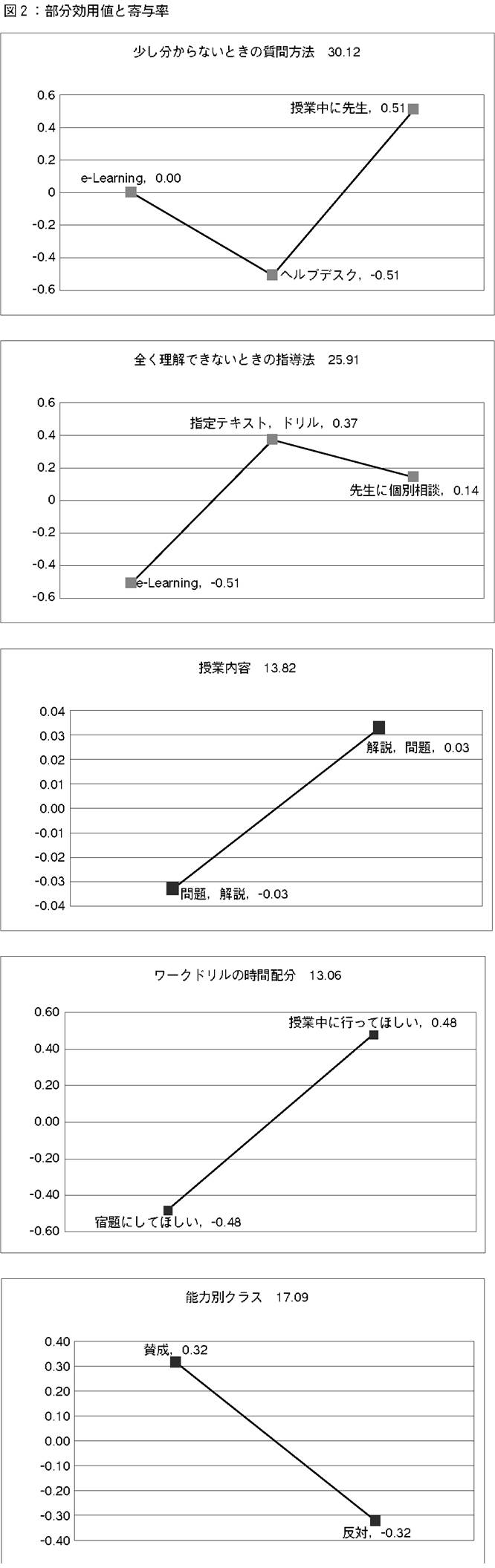
�}2�ɁC�e�����̕������p�l�Ȃ�тɊ�^���������B��^���Ƃ́C�����̒��ŁC�ǂ̑������I�D�����肷��ɓ�����d�v�ȗv�f�ƂȂ��Ă��邩��\���C���葮���̏d���x�ł���C��ʓI�ɂ́i1�j���p�l�̐U�ꕝ�ɂ��Z�o���@�C�i2�j���p�l�̕��U�̔�ɂ��Z�o���@��2��ނ�����[8]�B�{���͂ł́C�i2�j��p�����B
�s�A�\���̑��W���́C�ϑ����ʁi�팱�҂ɂ��I�D���ʕt���j�ƁC���菇�ʁi���肳�ꂽ�������p���瓱���o����鏇�ʁj�Ƃ̊Ԃ̑��W���ł���B1�ɋ߂��قǁC���͌��ʂ��Ó��ł���Ɖ��߂ł���B�{���͂ł�0.938�ł���C�Ó��ł��邱�Ƃ�������B�܂��C�P���h�[���̏��ʑ��W���Ƃ́C���ʕϐ��Ɋւ��鑊�W���ł���B1�ɋ߂��قǁC�Ó��ł���Ɖ��߂ł���B�{���͂ł́C0.717�ł���C�Ó��ł��邱�Ƃ�������B
�e�����̊�^��������ƁC�ȉ��̏��ƂȂ�C�����u����������Ȃ��Ƃ��̎�����@�v�y�сu�S�������ł��Ȃ��Ƃ��̎w���@�v���C��^���C30.12���C�y�� 25.91���ƁC���ɔ�ׂč�����^���ƂȂ��Ă���B
�@�@����������Ȃ��Ƃ��̎�����@ 30.12��
�A�@�S�������ł��Ȃ��Ƃ��̎w���@ 25.91��
�B�@�\�͕ʕҐ��N���X 17.09��
�C�@���Ɠ��e�̏��� 13.82��
�D�@���[�N�h�����̎��Ԕz�� 13.06��
�������p�l�͐��̒l�������Ă��鐅�����C�I�D�x�������Ɖ��߂���i�}2�Q�Ɓj�B
�����u����������Ȃ����̎�����@�v�Ɋւ��ẮC�u���ƒ��ɋ��t�Ɏ���v�̌��p�l�������C���Łue-Learning�v�͒��ԓI�ʒu�ł���C�u�@���ɂ��w���v�f�X�N�v�͒Ⴉ�����B���̌��ʂ���w���́C�u����������Ȃ��Ƃ��̎�����@�v�Ƃ��ĉ@���ɂ��w���v�f�X�N�́Ce-Learning�����I�D�x���Ⴂ���Ƃ����炩�ɂȂ����B�w���v�f�X�N���J�݂���ꍇ�ɂ́C���̂��Ƃ𗝉����C�w���v�f�X�N�̃V�X�e�����ɔz������K�v�����邩������Ȃ��B
�����u�S�������ł��Ȃ����̎w���@�v�Ɋւ��ẮC�u�w��e�L�X�g�C�h�����v���Łu���t�Ɍʂɑ��k�v�̌��p�l�������C�ue-Learning�v�͒Ⴉ�����B���̌��ʂ���C�S�������ł��Ȃ��y299�Łz�w���̎w���@�Ƃ��ẮC���̍����e�L�X�g���]�܂�Ă��邱�Ƃ�������B
�����u�\�͕ʕҐ��N���X�v�́C��^��17.09���ŁC��3�Ԗڂɏd�v������Ă���B�\�͕ʕҐ��Ɋւ��ẮC�^���̂ق������������p�l�����������B�܂��C�u���Ɠ��e�̏��ԁv�Ɋւ��ẮC0.03�Ƃ킸���ł͂��邪�C�]���ʂ�́u���������v�Ƃ����ق����C���p�l�����������B�����u���[�N�h�����̎��Ԕz���v�́C�u���ƒ��ɂ��Ăق����v���C���p�l�����������B
�Ō�ɁC�S�������ł��Ȃ��Ƃ��̎w���@�Ƃ��āC�ue-Learning�V�X�e���v�̌��p�l���Ⴉ�������Ƃɂ��āC�l�@���s���B����e-Learning�V�X�e���̌����҂ł���C�����ł��V�X�e���\�z���s���C���Ƃɗp���Ă���[9-13]�B����e-Learning�V�X�e���́C����ɂ�����R�X�g�Ƌ�����e�̎��Ƃ̃o�����X���l������ł̑Ë��_�ƂȂ������ł���ƍl���Ă���B���z�I�ȋ�����Ƃ́C���l���N���X�̋��t�Ƃ̑Θb�ɂ�鋳��Ə�X�l���Ă���̂ŁC���̓_�ł́C�u�搶�Ɍʂɑ��k�v�̂ق����ue-Learning�v�������p�l�������Ƃ�������̌��ʂɑ��ẮC�[�����C�܂����g�����B
���Ɂu�w��e�L�X�g�E�h�����v�Ɓue-Learning�V�X�e���v���r����B e-Learning�V�X�e���̗����Ƃ��āC�J��Ԃ��w�K���\�Ȃ��ƁC�������x���̋���R���e���c��24���ԁC�ǂ�����ł��A�N�Z�X�\�ł��邱�Ƃ��������邪�C�u�w��e�L�X�g�E�h�����v�ɂ����Ă��C�����͎����\�ł���B���ɐ��w��e-Learning�V�X�e���ł́C�����̓��̖͂������݂���̂ŁC�e�L�X�g�̗����̂ق����������̂ƌ����邾�낤�B����̒�������Ce-Learning�V�X�e���̔��W�͌����ł͂��邪�C�܂���y���Ɨ����̓_�ł́C�u�w��e�L�X�g�E�h�����v�̂ق������p�l�������C�Ɗw���͍l���Ă��邱�Ƃ��������ꂽ�B
�T�D�܂Ƃ�
�{�_���ł́C�o�c�w�Ȃɂ����鐔�w���Ƃ����P���邽�߁C�w�����l���闝�z�̐��w������Ɋւ���I�D�͂����B����̒����ɂ��C�{�w�o�c�w�Ȃ̊w���̐��w�̎��Ƃɑ���v�]���R���W���C���g���͂ɂ���ʉ����邱�Ƃ��ł����B���͎�@�Ƃ��ẮC�o�c�w�Ȃ̐��w�֘A�̎��Ƃ̎�u�҂�ΏۂɁC�A���P�[�g�������s���C�R���W���C���g���͂��s�����B
���ʂƂ��āC�w���́C�u����������Ȃ��Ƃ��̎�����@�v���ŏd�v�����C����Ɋւ��Ắu���ƒ��ɐ搶�Ɏ���v�̌��p�l�������C�t�Ɂu�@���ɂ��w���v�f�X�N�v���Ⴉ�����B���ɏd�v������Ă��鑮���u�S�������ł��Ȃ����̎w���@�v�Ɋւ��ẮC�u�w��e�L�X�g�C�h�����v���Łu���t�Ɍʂɑ��k�v�̌��p�l�������C�ue-Learning�v�͒Ⴉ�����B���̌��ʂ���C�S�������ł��Ȃ��w���̎w���@�Ƃ��ẮC���̍����e�L�X�g���]�܂�Ă��邱�Ƃ����������B�����u�\�͕ʕҐ��N���X�v�́C��3�Ԗڂɏd�v������Ă���B�\�͕ʕҐ��Ɋւ��ẮC�^���̂ق������������p�l�����������B
���_�Ƃ��ẮC�w�����ł��d�v���������́C�u����������Ȃ��Ƃ��̎�����@�v�ł���C����Ɋւ��ẮC�]���ʂ�́u���ƒ��ɐ搶�Ɏ���v�̌��p�l���������Ƃ����炩�ɂȂ����B
�ӎ�
�e���I����ɂ�����C�f�[�^���͂���`���Ă��ꂽ���c�[�~�̐A�ؗI从q����Ɋ��ӂ������܂��B�܂��C�M�d�Ȏ��Ǝ��ԂɃA���P�[�g�����ɋ��͂��Ă��ꂽ�w���̊F�l�ɁC���߂Ċ��ӂ������܂��B
�y300�Łz
�y301�Łz
�Q�l����
[1]�@�^��m�ȁC�g���{���̓��ꋳ�珔�w�Z�����̑�w�ɂ����鋳��Ƌ���擾�ւ̗v�]�Ɋւ��钲���C�h���{���B��Q�w�� �ҁ^���{���B��Q�w���Cvol. 20�Cno. 3�Cpp. 91-97�C1998�B
[2]�@�^��m�ȁCSPSS�ɂ��R���W���C���g����−����E�S���E��������ł̊��p�@�C�����}���C2001�B
[3]�@����֎q�C�k���r��C���B��� ���C�g��w�ɂ�������ƕ]���Ǝ��Ɖ��P�̘A�g : �R���W���C���g���͂����p���āh�C ���{������w���20��N��_���W�Cvol. 20�Cpp. 138-141 2004�B
[4]�@��c�O�C�g�R���W���C���g���̗͂��_�Ɖۑ�h�CAHP�ƃR���W���C���g�����C�؉��h���C���h���i�ҁj�Cpp. 123-158�C���㐔�w�ЁC2004�B
�y302�Łz[5]�@����j�C���ї��u�C���R�T ���C�g�u�`�E�u���V�[�������ɂ�����X���C�h����щ������̌�����o���Ɋ�Â����[�U�[�|�C���^���̃t�B���^�����O�h�C����w����C�f�[�^�x�[�X�E�V�X�e��������C�Вc�@�l����w�� �ie-Learning�C�Ẵf�[�^�x�[�X���[�N�V���b�vDBWS 2006�j�Cvol. 2006�Cno. 77�Cpp. 7-13�C2006�B
[6]�@�R��T�I�C�����i�C�c�_��C�È���� ���C�g�u�`�����F���ɂ�����u�`�X���C�h���̗��p�C�h�d�q���ʐM�w��Z�p�����CNLC�C���ꗝ���ƃR�~���j�P�[�V�����Cvol. 106�Cno. 442�Cpp. 43-48�C2006�B
[7]�@�������F�C���� ���ϗʉ�͂̎��ہi��2�Łj�C�u�k�ЁC2000�B
[8]�@���쒩�q�C�g���i�R���Z�v�g�̖��͓x�̐��ʓI�c��:�R���W���C���g���͂ɂ��I�D�\����́h�C�i���@�Вc�@�l���{�i���Ǘ��w���Cvol. 24�Cno. 3�Cpp. 28-34�C1994�B
[9]�@���c�R�����C�g���w�pWeb���ނ̌����I�������@�h�C���{�o�c���w��C���{�o�c���w���Cvol. 27�Cno. 2�Cpp. 71-81�C2005�B
[10]�@Y.
Shirota�C�gA Semantic
Explanation and Symbolic Computation Approach for Designing Mathematical
Courseware,�h in Proceedings of the Third International
Conference on Creating, Connecting and Collaborating through Computing, IEEE
Computer Society, 2005, pp. 158-165.
[11]�@���c�R�����C�g�o�ύœK�������Ƃ��鐔�wWeb���ގ����쐬�V�X�e���h�C�w�K�@��w�o�Ϙ_�W�Cvol. 41�Cno. 1�Cpp. 1-15�C2004�B
[12]�@���c�R�����C�g�A�N�Z�X�r���e�B�ƊJ���R�X�g���d�������}���`���f�B�A����x���V�X�e���̍\�z�C�h���{�o�c���w��C���{�o�c���w���Cvol. 25�Cno. 2�Cpp. 127-140�C2003�B
[13]�@���c�R�����C�g���w�pWeb���ގ��������̂��߂̋��ޓ��e�̈Ӗ��Ɋւ���XML�^�O��`�h�C�{�K�@��{�S�Z�_�W�Cvol. 41�Cno. 4�Cpp. 281-294�C2005�B