�y31�Łz
�O���o�ϐ��̍l�@�i���v�Ȗʕ��́����̂Q���j
�\�\���Љ�։v�̍ő剻�ƍœK���v�����C�œK�ېŊz�C�y�эœK�⏕���z�\�\
��C�@�������A�쓈�@�C�F�����A�����@�K�V��
�P�@�͂��߂�
�{�e�̍l�@�������ė��O�e�P�j�ł́C�u�w����T�[�r�X�̏����ʂ��ď���҂��o������p�̐����ɉe�����y�ڂ��x�O���o�ϐ��i���y�ѕ��j���I�ɓ��܂���v���v�Ȗʂ̍\�z�����݁C���ȖʂɊ�Â����o���v�Ȑ��Q�j�ƌ��E�Љ�։v�Ȑ��R�j�����߂��B�{�e�ł͂���2�Ȑ��S�j�ɁC���i�Ȑ��y�т���ɑΉ�������E�Љ��p�Ȑ���������4�{�̋Ȑ��ɏƏ��āC����3�_���l�@����B
�y32�Łz�i1�j�ő�̎Љ�։v�T�j�������v�����i�����C�œK���v�����j�C
�i2�j�ő�̎Љ�։v�����ېŒ����z�i�����C�œK�ېŊz�U�j�j�C
�i3�j�ő�̎Љ�։v�����⏕����t�z�i�����C�œK�⏕���z�V�j�j�B
��L�̖ړI�ɏƂ炵�{�e�ł͎��̑�2�߂ŁC�O�e�ō\�z�E�ᖡ����5��ނ̎��v�Ȗʂ���3��ނ̎��v�Ȗʁi���l��|1�C2�y��3�j��I�����C�����̎��v�Ȗʋy�ѓ��Ȗʏ�𑖂鏀���o���v�Ȑ��C���тɊe���v�ȖʂɊ�Â����߂��铱�o���v�Ȑ��y�ь��E�Љ�։v�Ȑ��ɂ��āC�����̓������ȒP�ɍĐ�������B��3�߂ł́C2��ނ̉��i�Ȑ�������ƂƂ��ɁC�e�X�̉��i�Ȑ��ɑΉ�������E�Љ��p�Ȑ��ɂ��ĐG���B�ȏ�̏�����Ƃ̌�C�{�e���f�����v�e�[�}�̍l�@�Ɉڂ�C�œK���v�����C�œK�ېŊz�y�эœK�⏕���z�ɂ��đ�4�߂Ř_����B�Ō�ɁC�܂Ƃ߂̍l�@���5�߂ŊȒP�ɋL���B
�Q�@3��ނ̎��v�Ȗ�
�Q�|�P�@���v�ȖʂƏ����o���v�Ȑ�
�u����T�[�r�X�̏������҂������p�����������v�̈����ɓ��Y�T�[�r�X�ɑ��鉼�z�ύt���v�����W�j���܂߂�ϓ_�ɗ����C�����������W���̈�Ɍ����钼��3���W���i�����C���v����N�C���i����P�C�y�щ��z�ύt���v����M��v�X�Ӗ�����3�{�̒������W���j�ɂ���č\�������3������ԓ��ɁC5��ނ̎��v�Ȗʂ�O�e�ł͕`�o�����B�{�e�ł͂����̂����C����3��ނ̎��v�Ȗʁi�����C���l��1�`3�ɓ�������v�Ȗʁj���l�@�̑Ώۂɐ�����B
�i1�j���l��|1�F�uM�̑S�l��ɘi��O���s�o�ϐ��i���y�ѕ��j��S�����܂��Ȃ��v���v�� �@�@�@�@�@���X�j
�@�@�@���v�Ȗʔ����FP��0.72�|N2�{0�~M�B
�@�@�@�@�@�@�@�@�@�@�A���C0.0��M��2.0�CN��0 ����P��0�B
�i2�j���l��|2�F�u�O���o�ϐ��i���y�ѕ��j�Ɋւ��Ē����I�ȕ����ƊO���s�o�ϐ�����܂� �@�@�@�@�@ �镔�������ɗL����v���v�Ȗ�
�y33�Łz�@�@�@���v�Ȗʔ����F�@0.0��M��0.4 �̂Ƃ��CP��2�|N2�{0�~M�B
�@�@�@�@�@�@�@�@�@�@�@�A���CN��0 ����P��0�B
�@�@�@�@�@�@�@�@�@�@�A0.4��M��1.4 �̂Ƃ��CP��2�|N2�|2�iM�|0.4�jN2�B
�@�@�@�@�@�@�@�@�@�@�@�A���CN��0 ����P��0�B
�i3�j���l��|3�F�u�O���o�ϐ��i���j���тɊO���s�o�ϐ������ɓ��܂���v���v�Ȗ�
�@�@�@���v�Ȗʔ����FP��2�|N2�|2�iM�|0.8�j2�B
�@�@�@�@�@�@�@�@�@�@�A���C0.0��M��2.0�CN��0 ����P��0�B
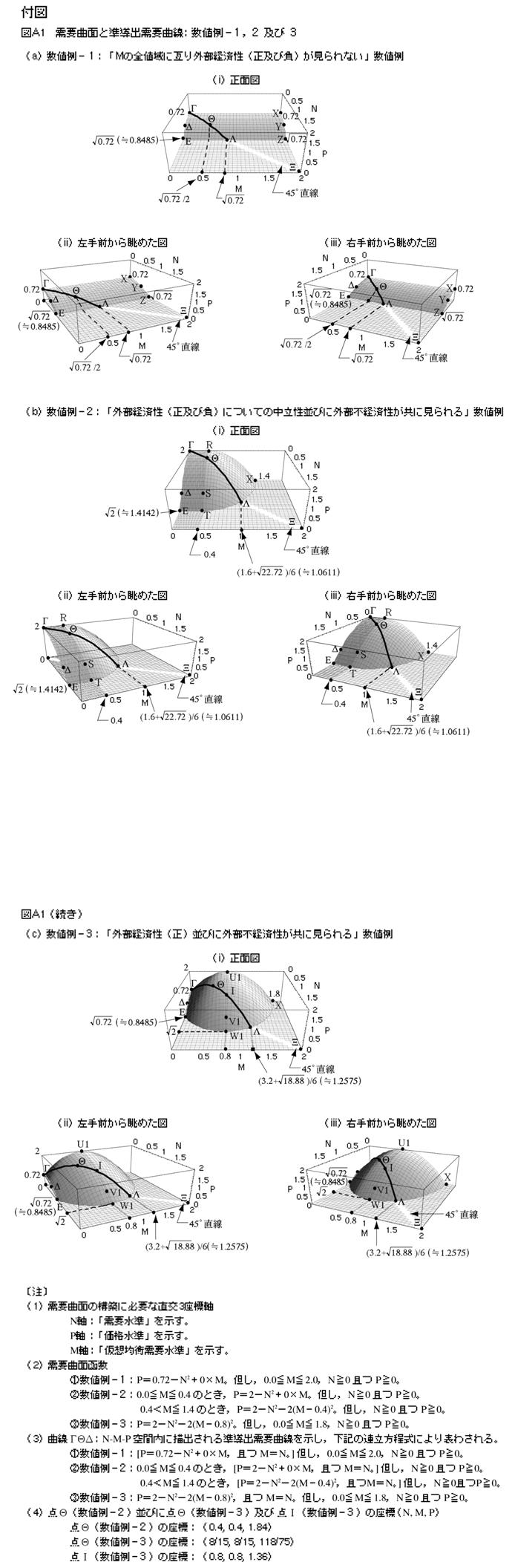
��L�̐��l��|1�C2�y��3���������v�Ȗʂ�N-M-P��ԓ��ɕ`���ƁC�t�}�̐}A1��B���}�̎��v�Ȗʏ�ɂ͏����o���v�Ȑ����C���l��ʂɃg���b�L���O�E���[�g�̃C���[�W10�j�ɂ��`����Ă���C�����͎��̘A���������ɂ��\�킳���B
�i1�j���l��|1�ɓ�������v�Ȗʏ�𑖂鏀���o���v�Ȑ�
�@�@�@P��0.72�|N2�{0�~M
�@�@�oM��N
�@�@�@�A���C0.0��M��2.0�CN��0 ���� P��0�B
�i2�j���l��|2�ɓ�������v�Ȗʏ�𑖂鏀���o���v�Ȑ�
�@�@�@0.0��M��0.4�̂Ƃ��C
�@�@�@P��2�|N2�{0�~M
�@�@�oM��N
�@�@�@�A���CN��0 ���� P��0�B
�@�@�A0.4��M��1.4�̂Ƃ��C
�@�@�@P��2�|N2�|2�iM�|0.4�j2
�@�@�oM��N
�@�@�@�A���CN��0 ���� P��0�B
�i3�j���l��|3�ɓ�������v�Ȗʏ�𑖂鏀���o���v�Ȑ�
�@�@P��2�|N2�|2�iM�|0.8�j2
�@�oM��N
�@�@�A���C0.0��M��1.8�CN��0�CP��0�B
�Q�|�Q�@���o���v�Ȑ��ƌ��E�Љ�։v�Ȑ�
���v�Ȗʏ�𑖂鏀���o���v�Ȑ���N-P���ʂ��ˉe����ƁC���o���v�Ȑ����w�I�ɓ�����B�㐔�I�ɂ́C���v�Ȗʔ��� h�iN, M�j�� M��N�������邱�Ƃɂ�蓾����B����ɂ�����v�ȖʂɈˋ����ċ��߂��铱�o���v�Ȑ��́C���l��ʂɎ��̗l�Ɏ������B
�i1�j���l��|1�ɓ�������v�ȖʂɊ�Â����߂��铱�o���v�Ȑ�
�@�@�@P��0.72�|N2�B
�@�@�@�A���CN��0 ���� P��0�B
�y34�Łz�i2�j���l��|2�ɓ�������v�ȖʂɊ�Â����߂��铱�o���v�Ȑ�
�@�@�@0.0��N��0.4�̂Ƃ��C
�@�@�@P��2�|N2�B
�@�@�A0.4��N�̂Ƃ��C
�@�@�@P��1.68�{1.6N�|3N2�B
�@�@�@�A���CP��0�B
�i3�j���l��|3�ɓ�������v�ȖʂɊ�Â����߂��铱�o���v�Ȑ�
�@�@P��0.72�{3.2N�|3N2�B
�@�@�A���CN��0 ���� P��0�B
�����C���E�Љ�։v�Ȑ��́C���L�̌v�Z����Ď��v�Ȗʂ��狁�߂���B
�@MSB�iN�j��dGCS�iN�j/dN
�@�@�@�@�@ ��
�@�@�A��MSB�iN�j�F���E�Љ�։v����11�j�C
�@�@�@�@ GCS�iN�j�F����җ]�蔟��12�j���͎Љ�։v����13�j
�@�@�@�@ h�iN, M�j�F���v�Ȗʔ����B
�v�Z�̌��ʁC���l��ʂɓ�������E�Љ�։v�Ȑ��́C���̂Ƃ���ł���B
�i1�j���l��|1�ɓ�������v�ȖʂɊ�Â����߂�����E�Љ�։v�Ȑ�
�@�@�@P��0.72�|N2�B
�@�@�@�A���CN��0 ���� P��0�B
�i2�j���l��|2�ɓ�������v�ȖʂɊ�Â����߂�����E�Љ�։v�Ȑ�
�@�@�@0.0��N��0.4�̂Ƃ��C
�@�@�@P��2�|N2�B
�@�@�A0.4��N�̂Ƃ��C
�@�@�@P��1.68�{3.2N�|7N2�B
�@�@�@�A���CP��0�B
�i3�j���l��|3�ɓ�������v�ȖʂɊ�Â����߂�����E�Љ�։v�Ȑ�
�@�@�@P��0.72�{6.4N�|7N2�B
�@�@�@�A���CN��0 ���� P��0�B
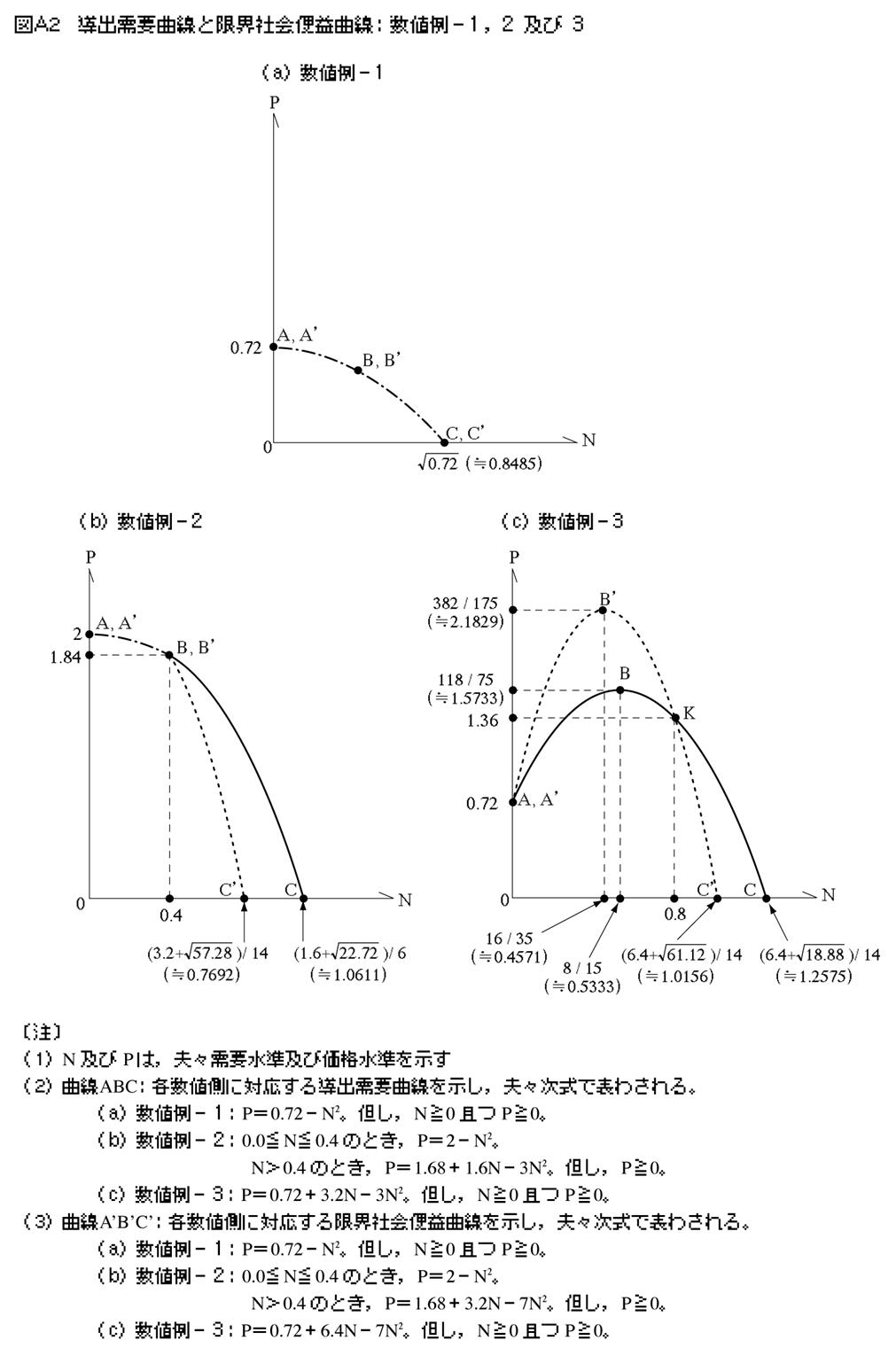
��ŋ��߂����o���v�Ȑ��ƌ��E�Љ��p�Ȑ����C���l��ʂɓ����N-P��ԓ��ɕ`���ƕt�}���y35�Łz�}A2��B���}�œ��o���v�Ȑ��ƌ��E�Љ�։v�Ȑ��̑��ΓI�ʒu�W������ƁC���l��|1�̏ꍇ�C���Ȑ��͈�v���C�P�������������B���l��|2�̏ꍇ�C0.0��N��0.4�̂Ƃ����Ȑ��͈�v���C�P�������������B���̌�N��0.4����ƁC���Ȑ��͘������͂��߂�B���̍ہC���E�Љ�։v�Ȑ��͓��o���v�Ȑ������������x�Ō�������̂ŁC�O�҂͌�҂̉����Ɉʒu���CN�̑����ƂƂ��ɗ��҂̘������͊g�傷��B���l��|3�̏ꍇ�C���Ȑ��݂͌��ɈقȂ�i�A���C��_K��N���W�l0.8�ɑ��Ă̂ݗ��҂͈�v����j���ɏ�����ɓʂł���B���E�Љ�։v�Ȑ���N��0.8�����̂Ƃ����o���v�Ȑ��̏㑤�Ɉʒu���CN��0.8����Ɠ��o���v�Ȑ��̉����Ɉʒu����B
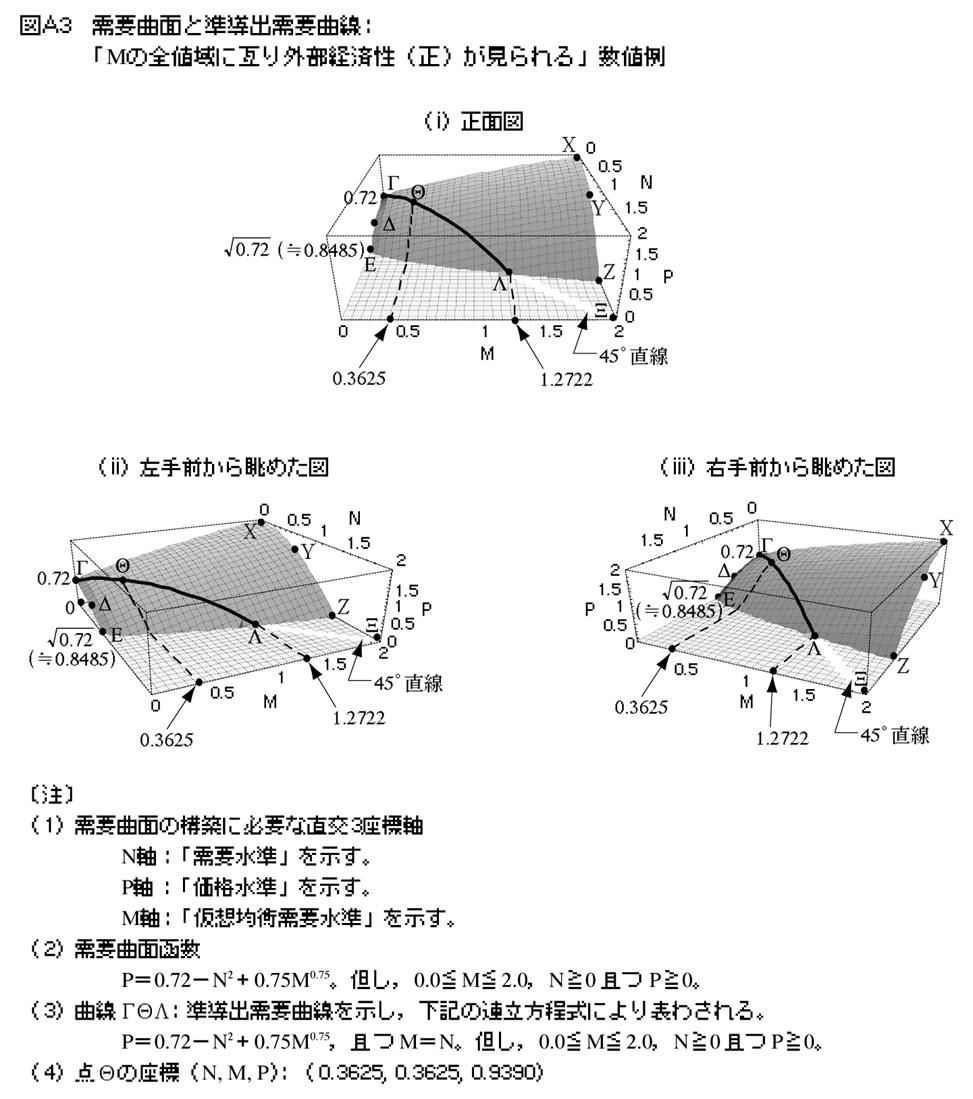
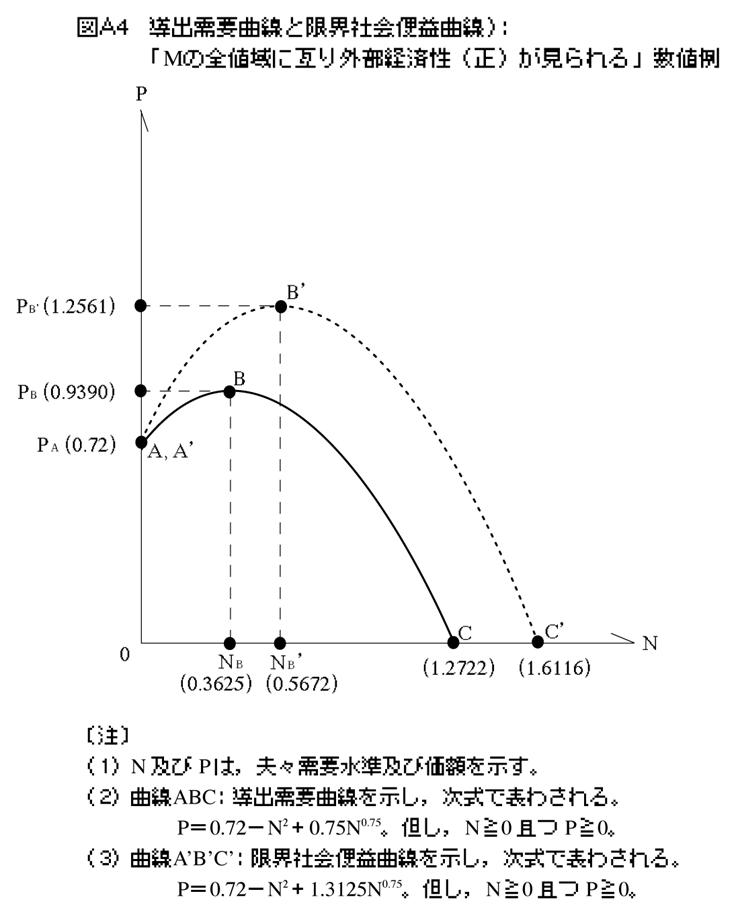
�����ŁC�uM�̑S�l��ɘi��O���o�ϐ��i���j����܂���v���v�Ȗʂ̐��l����C�Q�l�܂łɕt�}�̐}A314�j�ŏЉ�Ă����B���̎��v�ȖʂɊւ���u�Љ�։v�̍ő剻�����݂�œK���̍l�@�v�́C�{�e�ł͊������ʍe�ɏ��邪�C���ȖʂɊ�Â����߂��铱�o���v�Ȑ�15�j�ƌ��E�Љ�։v�Ȑ�16�j�ɂ��Ē��߂�ƁC�t�}�̐}A4�������Ƃ���C���ɏ�����ɓʂł���C�O�҂͏�Ɍ�҂̉����Ɉʒu����i�A���CN��0.0�̂Ƃ��͗��҈�v����j�B
�R�@2��ނ̉��i�Ȑ�
�R�|�P�@���i�Ȑ������ƌ��E�Љ��p�Ȑ�����
�{�e���������v�e�[�}�̍l�@�Ɍ������X�Ȃ鏀���Ƃ��āC���Ɏ����C����҂ɑ���2��ނ̉��i�Ȑ�������B17�j
�i1�j���i�Ȑ��ޗ�|A�F�u�O���o�ϐ��i���y�ѕ��j����܂��Ȃ��v���i�Ȑ�18�j
�@�@�@���i�Ȑ������FP��a�B
�@�@�@�@�@�@�@�@�@�@�A���Ca �͒萔�ia��0�j���� N��0.0�B
�i2�j���i�Ȑ��ޗ�|B�F�u�O���s�o�ϐ�����܂���v���i�Ȑ�19�j
�@�@�@���i�Ȑ������F�@0.0��N��0.4 �̂Ƃ��C
�@�@�@�@�@�@�@�@�@�@�@P�� b�B
�@�@�@�@�@�@�@�@�@�@�@�A���Cb �͒萔�ib��0�j�B
�y36�Łz�@�@�@�@�@�@�@�@�@�@�AN��0.4 �̂Ƃ��C
�@�@�@�@�@�@�@�@�@�@�@P�� b�{0.5�iN�|0.4�j2�B
�@�@�@�@�@�@�@�@�@�@�@�A���Cb �͒萔�ib��0�j�B
��œ����������i�Ȑ��Ɋ�Â��C���̌��E�Љ��p20�j�Ȑ����ޗ�ʂɋ��߂���B
�i1�j�ޗ�|A�ɑ����鉿�i�Ȑ��Ɋ�Â����߂�����E�Љ��p�Ȑ�
�@�@P�� a�B
�@�@�A���Ca �͒萔�ia��0�j���� N��0.0�B
�i2�j�ޗ�|B�ɑ����鉿�i�Ȑ��Ɋ�Â����߂�����E�Љ��p�Ȑ�
�@�@�@0.0��N��0.4 �̂Ƃ��C
�@�@�@P�� b�B
�@�@�@�A���Cb �͒萔�ib��0�j�B
�@�@�AN��0.4 �̂Ƃ��C
�@�@�@P�� b�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�@�@�@�A���Cb �͒萔�ib��0�j�B
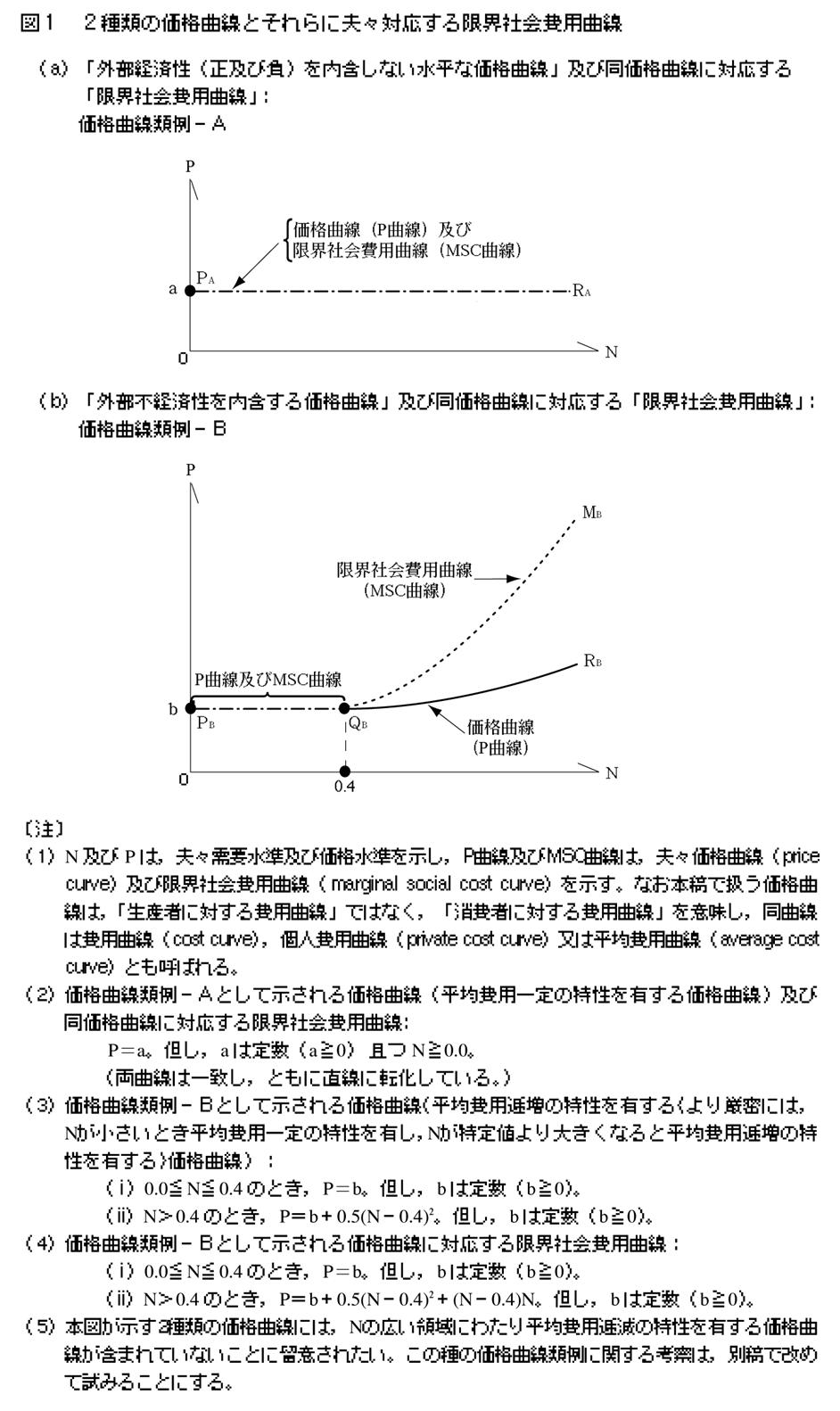
�R�|�Q�@���i�Ȑ��ƌ��E�Љ��p�Ȑ��̈ʒu�W
��q�������i�Ȑ��ƌ��E�Љ��p�Ȑ����C�����N-P��ԓ��ɗޗ�ʂɕ`���Ɛ}�P��B
���}���疾���炩�Ȃ悤�ɗޗ�|A�ɑ����鉿�i�Ȑ��̏ꍇ�C���iP��N�l�Ɋւ��Ȃ����i��a�j�ł���21�j�C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B����ɑ��ėޗ�|B�ɑ����鉿�i�Ȑ��̏ꍇ�C���iP��0.0��N��0.4 �̂Ƃ����i��b�j�ł���CN��0.4 �̂Ƃ���������22�j�B�y38�Łz�]���Č��E�Љ��p�Ȑ��́C0.0��N��0.4 �̂Ƃ����i�Ȑ��Ɉ�v���CN��0.4 �̂Ƃ����i�Ȑ��̏㑤�Ɉʒu����B�܂��C���҂̘�������N�̑����ƂƂ��Ɋg�傷��B
�Ƃ���ŁC��œ����������i�Ȑ��ޗ�ɂ́C�u�O���o�ϐ��i���j����܂���v���i�Ȑ�23�j���܂܂�Ă��Ȃ����C���̎�̗ޗ�ɑ����鉿�i�Ȑ���ΏۂƂ���Љ�։v�ő剻�̍l�@�́C�{�e�ł͊������ʍe�ʼn��߂Ď��݂�B
�S�@���Љ�։v�̍ő剻
�{�߂ł͂܂��C���Љ�։v���ő剻����菇�ɂ��ďq�ׂ�B�����ŁC��q����3��ނ̎��v�Ȗʁi���l��|1�`3�j�ɑ��āC���Љ�։v�̍ő剻�����݂�B24�j ���̍ہC���l�ᖈ�ɁC��q����2��ނ̉��i�Ȑ��ޗ�i�ޗ�|A�y��B�j�ɑ����鉿�i�Ȑ��̋�̓I�Ȕ����`���C�ݒ肷��B
�S�|�P�@�œK���̎菇�F�œK���v�����C�œK�ېŊz�C�y�эœK�⏕���z
�ȉ��ł́C���Љ�։v�̌v���w�W�Ƃ��āC�{�e�ł͑�����җ]��25�j��K�p���C���Љ�։v26�j�̍ő剻��_����B�Ȃ��C���Љ�։v���ő剻����C�œK���v�����C�œK�ېŊz�C�y�эœK�⏕���z�����߂��ʓI�Ȏ菇�́C�\�P�������Ƃ���ł���B

�y40�Łz���\�ɂ́C�O���t�ɋ���A�v���[�`�Ɛ����ɂ��A�v���[�`������Ă��邪�C�O�҂ɑ���菇�̗v�_��Z�߂�ƁC���̗l�ɐ����ł���B
�i1�j���E�Љ�։v�Ȑ��ƌ��E�Љ��p�Ȑ��̌�_���œK�_�ɂ�����C���̓_�ɑΉ�������v�������œK���v�����ƂȂ�B
�i2�j�œK�_��ʂ鐂�������o���v�Ȑ��y�щ��i�Ȑ��ƌ����_��v�XJT�y��JU�Ƃ���ƁC
�@�@�@�_JT���_JU�̏㑤�Ɉʒu����ꍇ�C����JTJU�̒������œK�ېŊz�ƂȂ�C
�@�@�A�_JT���_JU�̉����Ɉʒu����ꍇ�C����JUJT�̒������œK�⏕���z�ƂȂ�B27�j
���ہC�œK���̎菇�̎�ȑ_���́C�ȉ��̓_�ɂ���B�����C���i�Ȑ��Ɠ��o���v�Ȑ��̌�_���ύt�_�Ƃ��Ē�`����邪�C���́u�ύt�_�ɑΉ�������v�����i�����C�ύt���v�����j�v�ƁC�u�œK�_�ɑΉ�������v�����i�����C�œK���v�����j�v�̊Ԃɘ�����������ꍇ�C�ېŒ������͕⏕����t������u���i�ɂ����v�����v��ʂ��āC������̋ύt���v�������O�̍œK���v�����Ɉ�v�����邱�Ƃɂ���B28�j
��q�̎菇�͂��̈Ӗ��ŁC�����I�ɋύt�_���ېŒ����O���͕⏕����t�O�ɑ��݂��邱�Ƃ�O��ɒu���B�����������[�����ƂɎ��v�Ȗʕ��͓I�l�@�ł́C���̌�������������Ȃ��ꍇ29�j�ł��C�œK�⏕���z�̒l�����ɂ����艻�ł���B�Ⴆ�C���i�Ȑ�����ɓ��o���v�Ȑ��̏㑤�Ɉʒu���邪�̂ɋύt�_�����݂��Ȃ��ꍇ�ł��C���E�Љ�։v�Ȑ��ƌ��E�Љ��p�Ȑ��̌�_�i�����C�œK�_�j�����݂���C�u�l���������Љ�։v�v�̍ő剻�����œK�⏕���z���C���ɂ����艻�ł���B���̃e�[�}�ɂ��ẮC��S�|�S�߂ŃP�[�X�|3A6�y�уP�[�X�|3B4���ᖡ����ۂɉ��߂ď������_���C���v�Ȗʕ��͓I�A�v���[�`���\�Ƃ��邳���₩�Ș_���I�Ӌ��̒n�ɗV�ԁB
���āC���̑�S�|�Q�߂���͋�̓I�ȍœK���̍l�@���P�[�X�ʂɏ������݂邪�C���̑O�Ɉȉ���2�_30�j�ɂ��ĊȒP�ɕt�����Ă����B
�i1�j�œK�ېŊz�Ƃ��Ē��������Ŏ��̔z������s�K�ł���ƁC�\�P�������菇�ɏ]���Ă����Љ�։v�̍ő剻���K�������������Ȃ��B���l�Ȃ��Ƃ́C�œK�⏕���z�̕�U�E��t�ɕK�v�ȍ����̒��B����s�K�ȏꍇ�ɂ��C�N���蓾��B
�i2�j���v����31�j�����Y����C���E�T�[�r�X�ɑ���K�����i�����Ƃ��C���̐ݒ�K�͂�搂���v����Ɍ��E��p���i�`������32�j������B���������K�p������E�Љ��p�Ȑ��y41�Łz�́C���Y�҂ɑ��鉿�i�Ȑ�33�j���瓱���o�������̂ŁC�{�e�ŗp����C����҂ɑ��鉿�i�Ȑ�34�j���瓱���o�������E�Љ��p�Ȑ��Ƃ͈قȂ�B�]���āC�{�e�����݂���v�Ȗʕ��͓I�l�@���C�������o�ϊw�I�Ȍ��E��p���i�`�������̃p���_�C���ɓ���ޕ����ւ�����肵�čs����ŁC�ʓr�ɋ����Ȗʕ��͓I�l�@�̓W�J�������B
�S�|�Q�@�œK���̍l�@�F�P�[�X�|1A�y��1B
�����ł́C���l��|1�ɓ�������v�Ȗʂɑ��āC���Љ�։v�̍ő剻�����݂�B���̍ہC�ޗ�|A�ɑ������̓I�ȉ��i�Ȑ��Ɨޗ�|B�ɑ������̓I�ȉ��i�Ȑ����C�v�X����ݒ肷��B
4�|2�|1�@�P�[�X�|1A
�}�Q�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1E��ݒ肷��B
�@P��0.25�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�܂��{�P�[�X�ɉ����āC���E�Љ�։v�Ȑ��͓��o���v�Ȑ�AEC�Ɉ�v����i�P�[�X�|1B�ɉ����Ă����l�j�B����āC�ύt�_�iE�j�ƍœK�_�iJ�j�͈�v����B���R�̂��ƂȂ���C�ύt���iNE�j�ƍœK���iNJ�j�͈�v����̂ŁC���b�Z�E�t�F�[���s��͏��Љ�։v�̍ő剻����������B�]���āC�O���s�o�ϐ��̔�����}������ړI�̉ېŒ������C�O���o�ϐ��i���j�̔����𑣂��ړI�̕⏕����t���C�Ƃ��ɕs�v�ł���B�Ȃ��C���b�Z�E�t�F�[���s��̋@�\�ɂ�莩��ő剻����Ă��鏃�Љ�։v�́C�}�`AP1J�̖ʐρi0.2148�j�ɓ������B
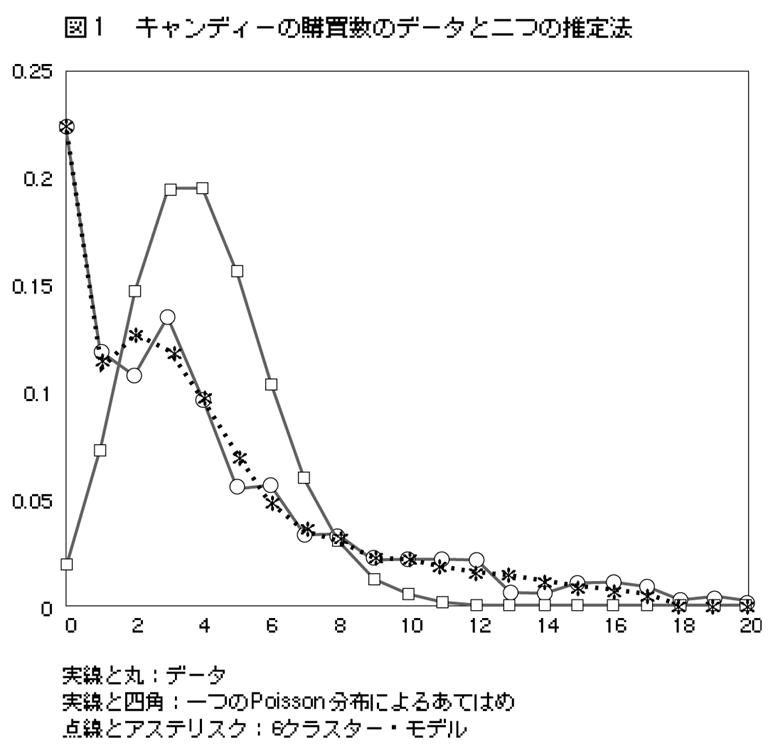
�S�|�Q�|�Q�@�P�[�X�|1B
�}�R�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1QE��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��0.25�B
�@N��0.4 �̂Ƃ��CP��0.25�{0.5�iN�|0.4�j2�B
���̂Ƃ��C���E�Љ��p�Ȑ�P1QJ�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��0.25�B
�@N��0.4 �̂Ƃ��CP��0.25�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C�ύt�_�iE�j�ƍœK�_�iJ�j�͈قȂ�B����āC�ύt���iNE�j�ƍœK���iNJ�j�͘������C�O�҂͌�҂��傫�Ȓl�������B�]���āC���Љ�։v���ő剻���邽�߂ɂ́C�u��p���ʂŐ�����O���s�o�ϐ��i���p�ʂŐ�����O���s�o�ϐ��ł͂Ȃ��j�v�̔�����}������ېł̒����ɂ��C�ύt���̒l���œK���̒l�ɂ܂ň���������K�v������B���̍ۂɓK�p���ׂ��œK�ېŊz�́C����JTJU�̒����i0.1091�j�ɓ������C���Љ�։v�̍ő�l�͐}�`AP1QJ�̖ʐρi0.1982�j�ɓ������B
�y44�Łz�S�|�R�@�œK���̍l�@�F�P�[�X�|2A�y��2B
�����ł́C���l��|2�ɓ�������v�Ȗʂɑ��āC���Љ�։v�̍ő剻�����݂�B���̍ہC�ޗ�|A�ɑ������̓I�ȉ��i�Ȑ����C�ޗ�|B�ɑ������̓I�ȉ��i�Ȑ�����ݒ肷��B
�S�|�R�|�P�@�P�[�X�|2A1
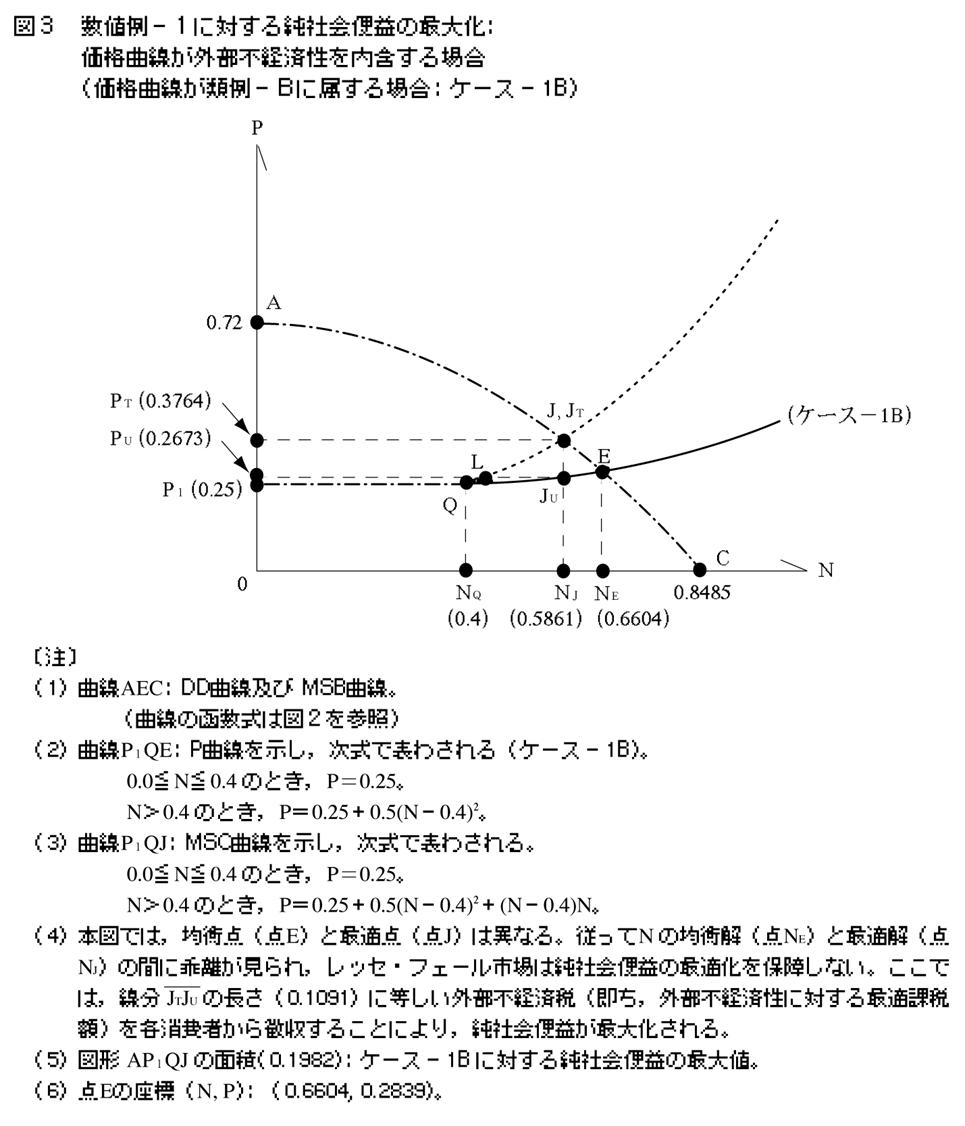
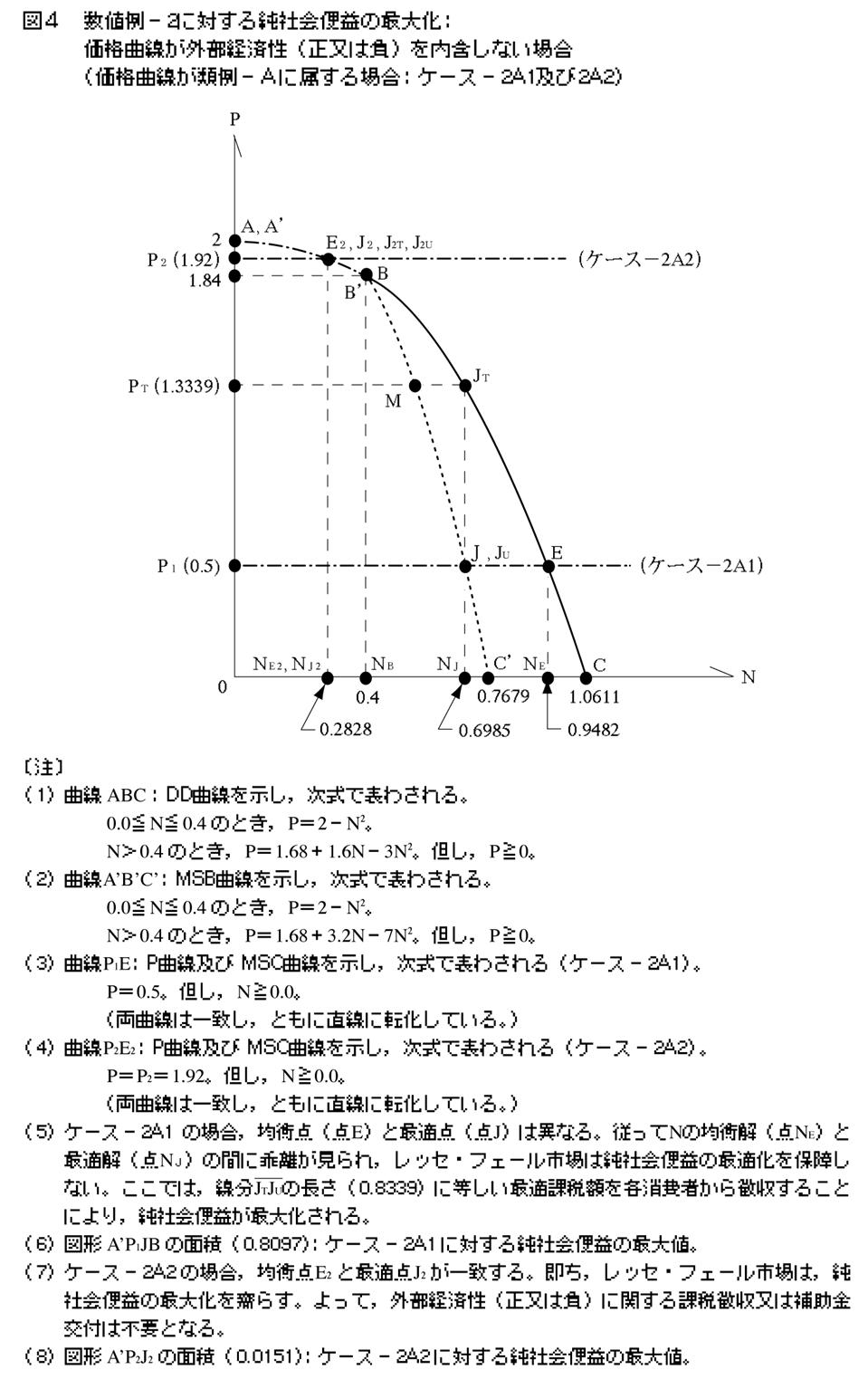
�}�S�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1E��ݒ肷��B
�@P��0.5�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�������C0��P��1.84�̂Ƃ��C���o���v�Ȑ�ABC�ƌ��E�Љ�։v�Ȑ�A�fB�fC�f�͈�v���邪�CP��1.84�̂Ƃ��C���Ȑ��͘�������i���o���v�Ȑ��ƌ��E�Љ��p�Ȑ��̊ԂɌ����邱�̊W�́C�P�[�X�|2A2�y�уP�[�X�|2B�ɉ����Ă����l�j�B����āC�ύt�_�iE�j�ƍœK�_�iJ�j�͈قȂ�C�ύt���iNE�j�ƍœK���iNJ�j�͘�������i�����ł�NE��NJ�j�B�]���āC���Љ�։v���ő剻���邽�߂ɂ́C�u���p���ʂŐ�����O���s�o�ϐ��i��p���ʂŐ�����O���s�o�ϐ��ł͂Ȃ��j�v�̔�����}������ېł̒����ɋ���C�ύt���̒l���œK���̒l�ɂ܂ň���������K�v������B���̍ۂɓK�p���ׂ��œK�ېŊz�́C����JTJU�̒����i0.8339�j�ɓ������C���Љ�։v�̍ő�l�͐}�`A�fP1JB�̖ʐρi0.8097�j�ɓ������B
�S�|�R�|�Q�@�P�[�X�|2A2
��}�i�}�S�j�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P2E2��ݒ肷��B
�@P��P2��1.92�B�A���CN��0.0�B
���̂Ƃ��C���i�Ȑ��C���E�Љ��p�Ȑ��C���o���v�Ȑ��C�y�ь��E�Љ�։v�Ȑ��̑��ΓI�ʒu�W�́C�P�[�X�|1A�Ɠ��l�ł���C�ύt�_E2�ƍœK�_J2�͈�v���C�ύt���iNE2�j�ƍœK���iNJ2�j����v����B�]���āC���b�Z�E�t�F�[���s��͎��珃�Љ�։v�̍ő剻����������̂ŁC�O���s�o�ϐ��i���y�ѕ��j�Ɋւ���ېŒ������C�⏕����t���C�Ƃ��ɕs�v�ł���B�Ȃ��C���b�Z�E�t�F�[���s��̋@�\�ɂ�莩��ő剻����Ă��鏃�Љ�։v�́C�}�`A�fP2J2�̖ʐρi0.0151�j�ɓ������B
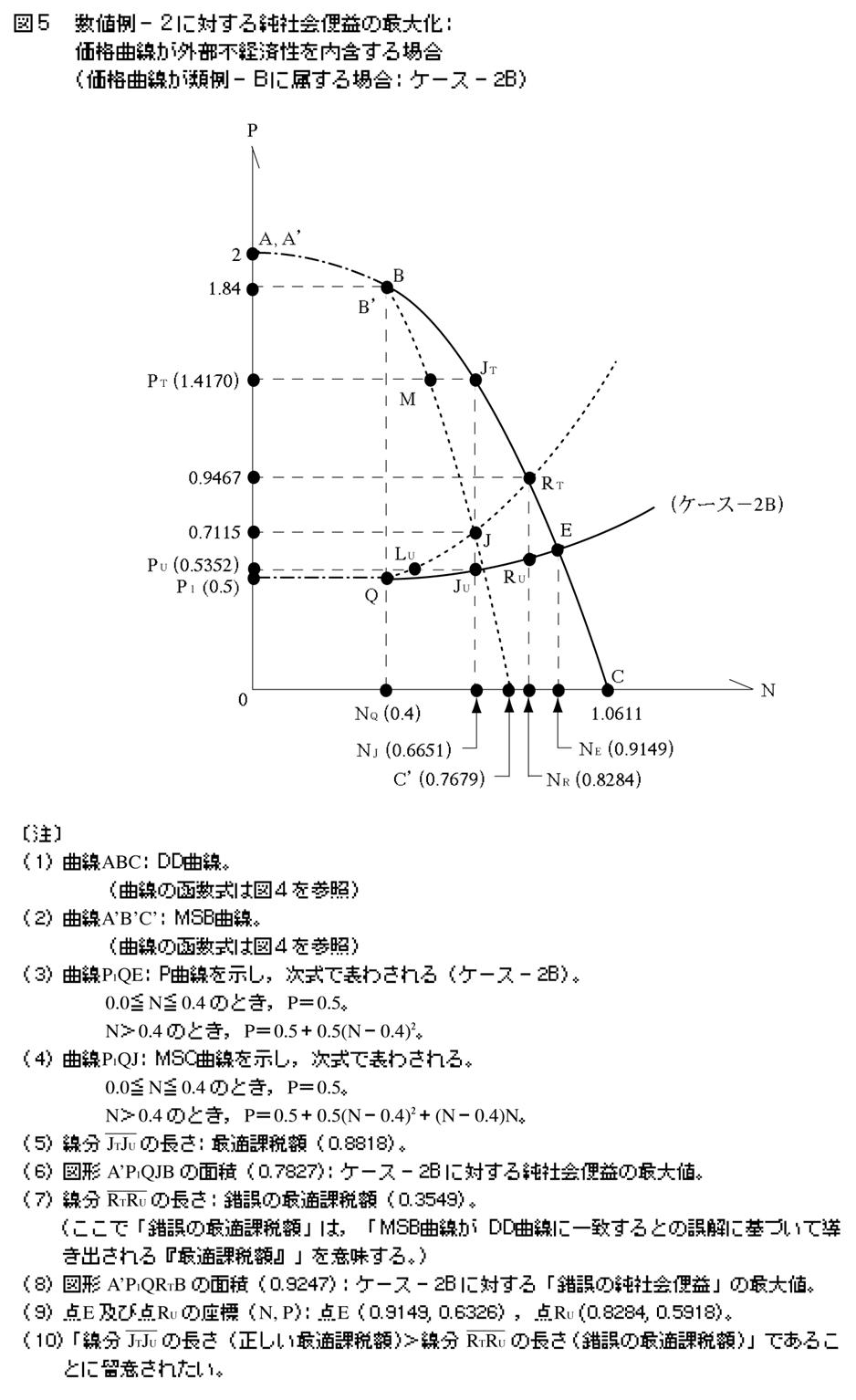
�S�|�R�|�R�@�P�[�X�|2B
�}�T�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1QE��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��0.5�B
�@N��0.4 �̂Ƃ��CP��0.5�{0.5�iN�|0.4�j2�B
���̂Ƃ��C���E�Љ��p�Ȑ�P1QJ�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��0.5�B
�@N��0.4 �̂Ƃ��CP��0.5�{0.5�iN�|0.4�j2�{0.5�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C�ύt�_�iE�j�ƍœK�_�iJ�j�͈قȂ�B����ċύt���iN�d�j�ƍœK���iN J �j�͘�������i�����ł�N�d��N J �j�B�]���āC���Љ�։v���ő剻���邽�߂ɂ́C�u���p���ʂŐ�����O���s�o�ϐ��v�Ɓu��p���ʂŐ�����O���s�o�ϐ��v��}�����y47�Łz��ېł̒����ɋ���C�ύt���̒l���œK���̒l�ɂ܂ň���������K�v������B���̍ۂɓK�p���ׂ��œK�ېŊz�́C����JTJU�̒����i0.8818�j�ɓ������C���Љ�։v�̍ő�l�͐}�`A�fP1QJB�̖ʐρi0.7827�j�ɓ������B
�lj��I�l�@�ɂȂ邪�C��ʍ��G���ۂ������Ă��鎩���ԓ��H�̗��p�ҁi�����C���H�T�[�r�X�̏���ҁj���o������p�����́C�ʏ�C��ʗʂ̑����ƂƂ��ɒቺ����B�����ɁC���H���p�ɔ��Ȃ����ϔ�p�i�����C�e���H���p�Ҍl�̋��K�I�x�o�z�j�͒�������B���̂悤�ɁC���H�T�[�r�X�̏���҂���ʍ��G�̊O���s�o�ϐ��̂ɖւ�u���p�����̒ቺ�ƕ��ϔ�p�̒����v���I�ɔz�����āC���Љ�։v�̍ő剻���l�@����ۂɂ́C�u���p���ʂŐ�����O���s�o�ϐ����I�ɓ��܂�����v�ȖʂɊ�Â����߂��铱�o���v�Ȑ��ƌ��E�Љ�։v�Ȑ��v�ɋ���C�{�P�[�X�i�����C�P�[�X�|2B�j�̍l�@�ɗނ��鎎�݂́C�P�[�X�|1B�̍l�@�ɗނ��鎎�݂������K�ł���悤�Ɏv����B���������ł���Ƃ���C�u�P�[�X�|1B�ɉ�����œK�ېŊz�i����JTJU�̒����j�v�ɑΉ�����u�{�P�[�X�ɉ��������RTRU�̒����i0.3549�j�v�́C����̍œK�ېŊz�Ƃ������C�u�{�P�[�X�ɉ����ċ��߂���œK�ېŊz�i����JTJU�̒�����0.8819�j�v�ɔ�r�������炩�ɒႢ�l�������B
�S�|�S�@�œK���̍l�@�F�P�[�X�|3A�y��3B
�����ł͐��l��|3�ɓ�������v�Ȗʂɑ��āC���Љ�։v�̍ő剻�����݂�B���̍ہC�ޗ�|A�ɑ������̓I�ȉ��i�Ȑ���Z�C�ޗ�|B�ɑ������̓I�ȉ��i���l�ݒ肷��B
�S�|�S�|�P�@�P�[�X�|3A1
�}�U�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1E��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��0.5�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C���o���v�Ȑ�ABC�ƌ��E�Љ�։v�Ȑ�A�fB�fC�f�͘������Ă���i�P�[�X�|3A2�`3A6�y�уP�[�X�|3B1�`3B4�ɉ����Ă����l�j�B����āC�ύt�_�iE�j�ƍœK�_�iJ�j�͈قȂ�C�ύt���iNE�j�ƍœK���iNJ�j�͘�������i�����ł�NENJ�j�B�]���āC���Љ�։v���ő剻���邽�߂ɂ̓P�[�X�|2A1�Ɠ������C�u���p���ʂŐ�����O���s�o�ϐ��v�ɑ���ېł̒����ɋ���C�ύt���̒l���œK���̒l�ɂ܂ň���������K�v������B���̍ۂɓK�p���ׂ��œK�ېŊz�́C����JTJU�̒����i0.5588�j�ɓ������C���Љ�։v�̍ő�l�͐}�`A�fP1JB�f�̖ʐρi1.0965�j�ɓ������B
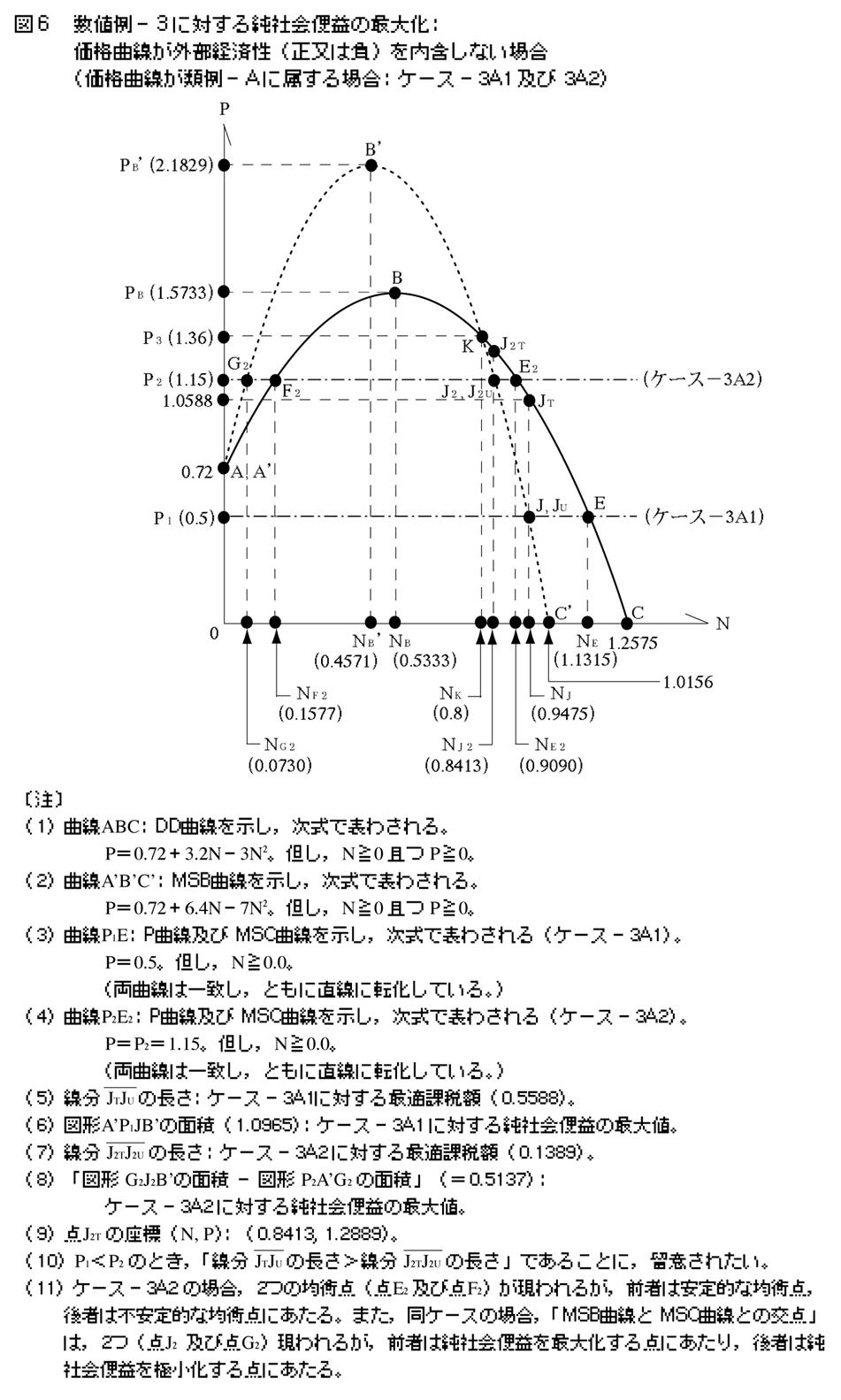
�S�|�S�|�Q�@�P�[�X�|3A2
��}�i�}�U�j�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P2E2��ݒ肷��B
�@P��P2��1.15�B�A���CN��0.0�B
���̂Ƃ��C�P�[�X�|3A1�̏ꍇ�Ɠ������R�ŁC���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C�ύt�_�iE2�j�ƍœK�_�iJ2�j�͈قȂ�C�ύt���iNE2�j�ƍœK���iNJ2�j�͘�������i�����ł�NE2��NJ2�j�B�]���āC���Љ�։v���ő剻���邽�߂ɂ́C�u���p�̑��ʂŐ�����O���s�o�ϐ��v��}������ېł̒������K�v�ƂȂ�B���̍ۂɓK�p���ׂ��œK�ېŊz�́C����J2TJ2U�̒����i0.1389�j�ɓ������C���Љ�։v�̍ő�l�́C�u�}�`G2J2B�f�̖ʐρ|�}�`P2A�fG2�̖ʐρv�y50�Łz�i0.5137�j�ɓ������B
�Ȃ��{�P�[�X�̏ꍇ�C��̋ύt�_�i�_E2�y�ѓ_F2�j������邪�C�_E2�͈���I�ȋύt�_�ɂ�����_F2�͕s����I�ȋύt�_�ɂ�����B�܂��C���E�Љ�։v�Ȑ��ƌ��E�Љ��p�Ȑ��̌�_����i�_J2�y�ѓ_G2�j����邪�C�_J2�͏��Љ�։v���ő剻���CG2�͏��Љ�։v���ɏ��ɂ���_�ɂ�����B

�S�|�S�|�R�@�P�[�X�|3A3
�}�V�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P3E3��ݒ肷��B
�@P��P3��1.36�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C���o���v�Ȑ��ƌ��E�Љ�։v�Ȑ��̌�_K��ɁC���܂��܋ύt�_�iE3�j�ƍœK�_�iJ3�j���d�Ȃ�B����āC�ύt���iNE3�j�ƍœK���iNJ3�j�͈�v����B����͓_K���C�u���p���ʂŐ�����O���o�ϐ��i���y�ѕ��j���C���̊O���o�ϐ����畉�̊O���o�ϐ��ɓ]������_�C�����O���o�ϐ��i���y�ѕ��j�Ɋւ��Ē����I�ȓ_�v�ɁC�����邱�Ƃ��Ӗ�����B��������C�_K���C�u�t�}A1�ic�j�ɉ����āC���v�Ȗʏ�𑖂鏀���o���v�Ȑ����C�O���o�ϐ��i���j����܂�����v�Ȗʕ�������O���s�o�ϐ�����܂�����v�Ȗʕ����ֈڍs����u�Ԃ̓_I�v�ɁC�Ή����邱�Ƃ��Ӗ�����B����̂ɖ{�P�[�X�ł́C���p���ʂŐ�����O���o�ϐ��i���y�ѕ��j�����݂���ɂ�������炸�C�O���o�ϐ��i�����͕��j�Ɋւ���ېŒ������͕⏕����t�͕s�v�ƂȂ�C���b�Z�E�t�F�[���s��̋@�\�ɂ�莩��ő剻����鏃�Љ�։v�́C�u�}�`G3J3B�f�̖ʐρ|�}�`P3A�fG3�̖ʐρv�i0.3413�j�ɓ������B�Ȃ��C�_F3�͕s����ȋύt�_�ɂ�����C�_G3�͏��Љ�։v���ɏ��ɂ���_�ɂ�����B
�S�|�S�|�S�@�P�[�X�|3A4
��}�i�}�V�j�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P4E4��ݒ肷��B
�@P��P4��1.52�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C�ύt�_�iE4�j�ƍœK�_�iJ4�j�͈قȂ�C����ċύt���iNE4�j�ƍœK���iNJ4�j�͘�������B�����ł́C�O�҂̒l�͌�҂̒l��菬�����B�]���āu���p���ʂŐ�����O���o�ϐ��i���j�v�̔����𑣂��⏕���̌�t�ɋ���C���Љ�։v�͍ő剻�����B���̍ۂɓK�p���ׂ��œK�⏕���z�͐���J4TJ4U�̒����i0.1075�j�ɓ������C���Љ�։v�̍ő�l�́u�}�`G4J4B�f�̖ʐρ|�}�`P4A�fG4�̖ʐρv�i0.2161�j�ɓ������B�Ȃ��C�_F4�͕s����ȋύt�_�ɂ�����C�_G4�͏��Љ�։v���ɏ��ɂ���_�ɂ�����B
�y52�Łz
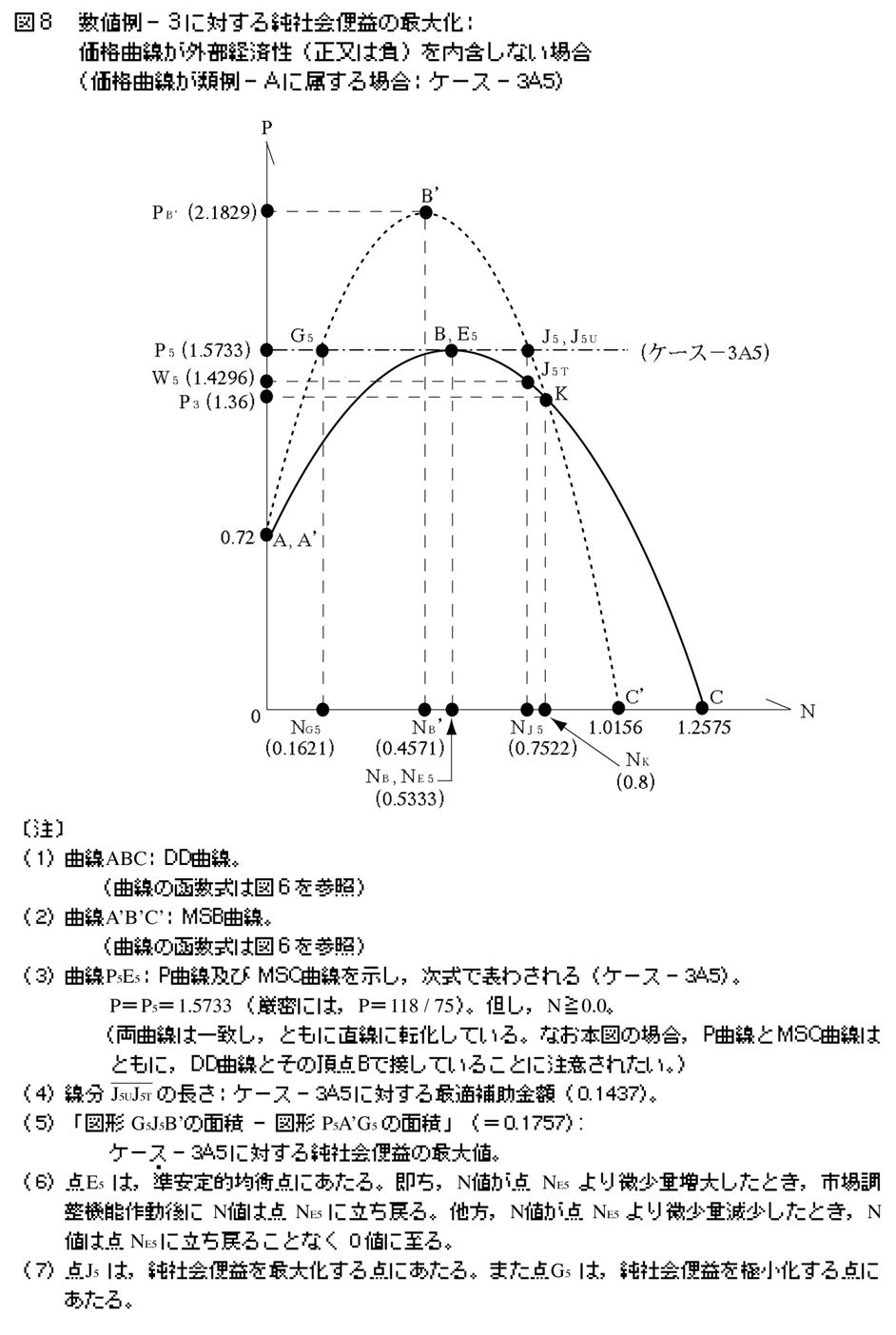
�S�|�S�|�T�@�P�[�X�|3A5
�}�W�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P5E5��ݒ肷��B
�@P��P5��1.5733�i�����ɂ́CP��118 / 75�j�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C�ύt�_�iE5�j�ƍœK�_�iJ5�j�͈قȂ�C�ύt���iNE5�j�ƍœK���iNJ5�j�͘�������i�����ł�NE5��NJ5�j�B�]���āC����J5UJ5T�̒����i0.1437�j�ɓ������C�u���p���ʂŐ�����O���o�ϐ��i���j�v�̔����𑣂��œK�⏕���z�̌�t�ɋ���C���Љ�։v�͍ő剻�����B���̂Ƃ����Љ�։v�̍ő�l�́C�u�}�`G5J5B�f�̖ʐρ|�}�`P5A�fG5�̖ʐρv�i0.1757�j�ɓ������B�Ȃ��C�ύt�_E5�́C���i�Ȑ�P5E5�����o���v�Ȑ�ABC�Ƃ��̒��_�Őڂ���_�ł��邽�߂ɁC������I�ύt�_�ƂȂ�B�����CN�l���_NE5�������ʑ��債�����ɂ́C�s�꒲���@�\�����N�l�͍ŏI�I�ɓ_NE5�̒l�ɉ�A����B�t��N�l���_NE5�̒l�������ʌ����������CN�l�͓_NE5�̒l�ɗ����߂邱�ƂȂ��ŏI�I�ɂ�0.0�l�Ɏ���B
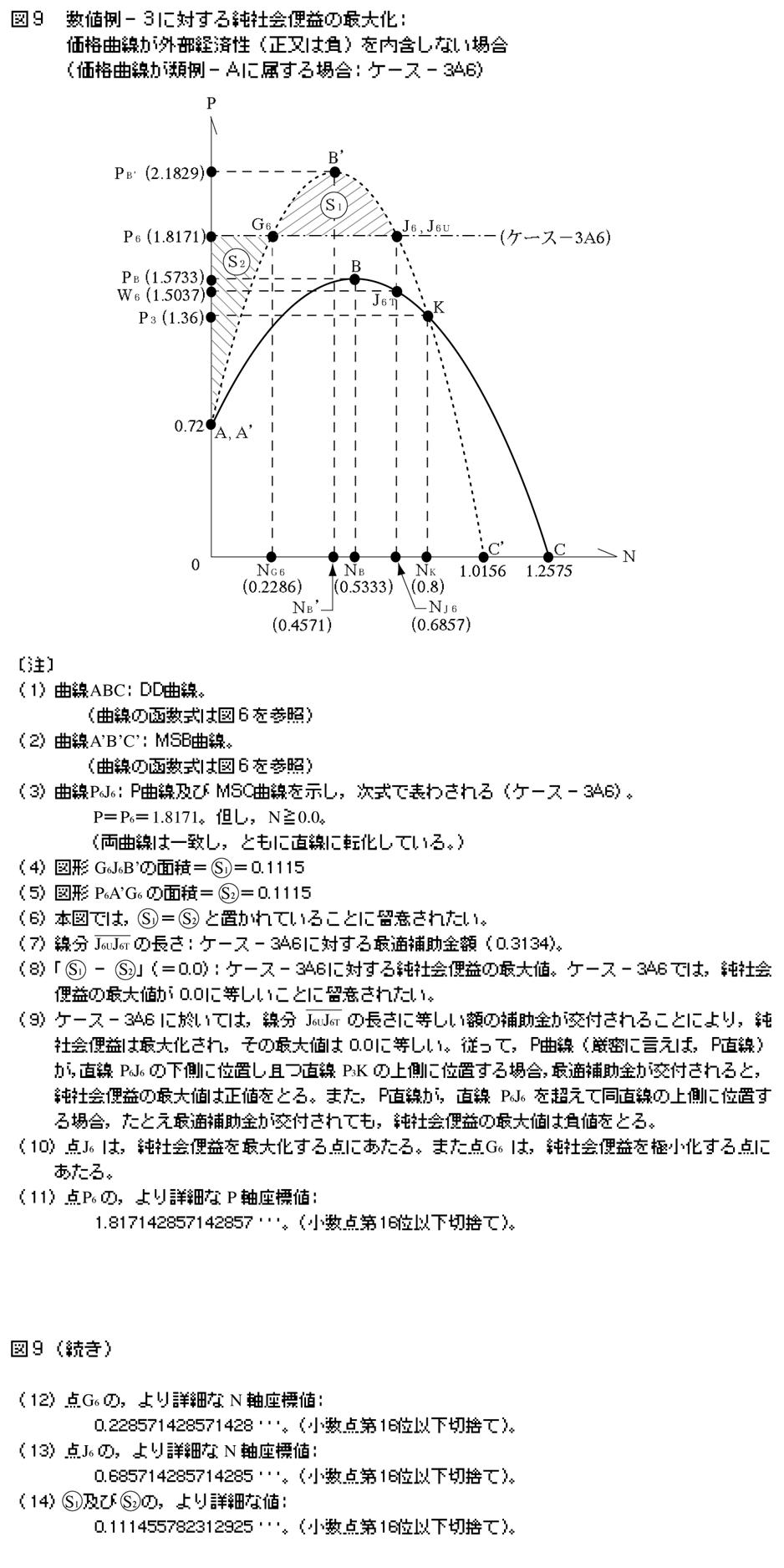
�S�|�S�|�U�@�P�[�X�|3A6
�}�X�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P6J6��ݒ肷��B
�@P��P6��1.8171�B�A���CN��0.0�B
���̂Ƃ��C���E�Љ��p�Ȑ��͉��i�Ȑ��Ɉ�v����B�����C���i�Ȑ�����ɓ��o���v�Ȑ��̏㑤�Ɉʒu���邽�߂ɁC�ύt�_�͑��݂��Ȃ��B�������C�œK�_�iJ6�j�͑��݂���B�]���āC����J6UJ6T�̒����i0.3134�j�ɓ������C�u���p���ʂŐ�����O���o�ϐ��i���j�v�𑣂��œK�⏕���z����肷�邱�Ƃ��ł���B���ہC���⏕���z�̌�t�ɂ�菃�Љ�։v�͍ő剻����C���̍ő�l�́u�}�`G6J6B�f�̖ʐρ|�}�`P6A�fG6�̖ʐρv�ɓ�����0.0�̒l���Ƃ�B
�ȏ�̎w�E�ƃP�[�X�|3A3�`3A5�ɂ��Ę_�������e���čl����Ɩ����炩�Ȃ悤�ɁC���ϔ�p���̓�����L���鉿�i�Ȑ��i�����C�����ȉ��i�����j������P3K�̏㑤�Ɉʒu���C������P6J6�̉����Ɉʒu����ꍇ�C�œK�Ȋz�̕⏕����t�ɋ��蓾���鏃�Љ�։v�̍ő�l�͐��l�������B�����C�����ȉ��i�������C����P6J6�̏㑤�Ɉʒu���C�����E�Љ�։v�Ȑ��̒��_B�f���z���Ȃ��ꍇ�ɂ́C���Ƃ��œK�ȓ_�ɑΉ����鏊���u�œK�Ȋz�̕⏕���v����t����Ă��C���̂Ƃ��ɓ����鏃�Љ�։v�̒l�͕��l�ƂȂ�B����āC���Љ�։v�̍ő�l��N��0.0�̂Ƃ�0.0�l���Ƃ�[�_���ɂȂ�B�Ȃ��C���i�������_B�f�̏㑤�Ɉʒu����ꍇ�C���Љ�։v�̒l��N�l�̌��������ƂȂ�̂ŁC�ő�l�͂��̂Ƃ����������[�_���ƂȂ�CN��0.0�̂Ƃ�0.0�������B
�y54�Łz
�S�|�S�|�V�@�P�[�X�|3B1
�}10�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�P1QE��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��0.5�B
�@N��0.4 �̂Ƃ��CP��0.5�{0.5�iN�|0.4�j2�B
���̂Ƃ��C���E�Љ��p�Ȑ�P1QJ�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��0.5�B
�@N��0.4 �� �Ƃ��CP��0.5�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C���i�Ȑ��C���E�Љ��p�Ȑ��C���o���v�Ȑ��y�ь��E�Љ�։v�Ȑ��̑��ΓI�ʒu�W�́C�P�[�X�|2B�Ɠ��l�ł���C�ύt�_�iE�j�ƍœK�_�iJ�j�͈قȂ�B����ċύt���iNE�j�ƍœK���iNJ�j�͘�������i�����ł�NE��NJ�j�B�]���āC���Љ�։v���ő剻���邽�߂ɂ́C�u���p���ʂŐ�����O���s�o�ϐ��v�Ɓu��p���ʂŐ�����O���s�o�ρv�𗼂�}������ېł̒����ɋ���C�ύt���̒l���œK���̒l�܂ň���������K�v������B���̍ۓK�p���ׂ��œK�ېŊz�́C����JTJU�̒����i0.6326�j�ɓ������C���Љ�։v�̍ő�l�͐}�`A�fP1QJB�f�̖ʐρi0.9809�j�ɓ������B����ɑ��C�P�[�X�|2B�ŐG�ꂽ����̍œK�ېŊz�́C����RTRU�̒����i0.4821�j�ɓ������B
4�|4�|8�@�P�[�X�|3B2
�}11�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�PB2Q2E2��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��1.4176�B
�@N��0.4 �Ƃ��CP��1.4176�{0.5�iN�|0.4�j2�B
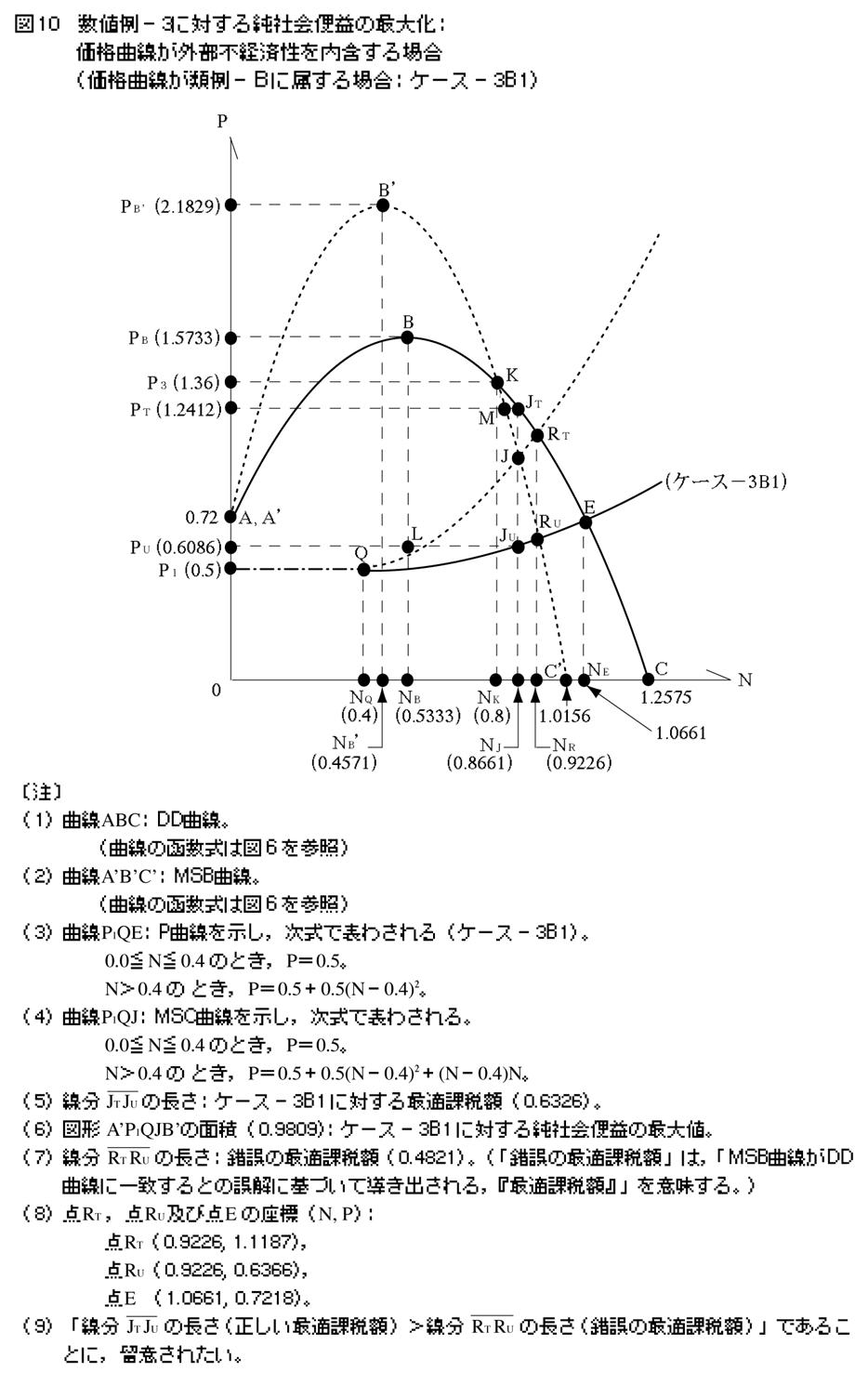
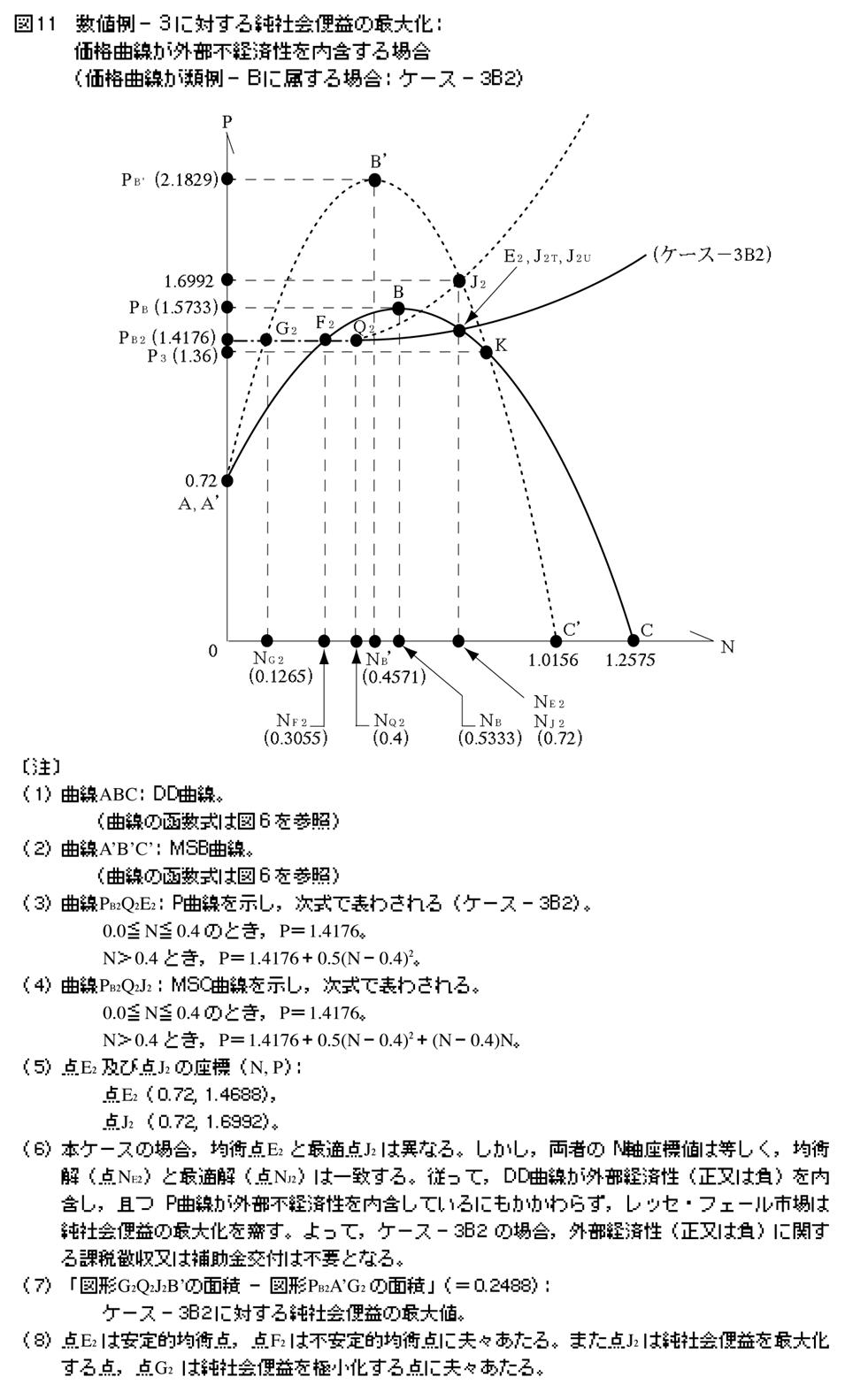
�y57�Łz���̂Ƃ��C���E�Љ��p�Ȑ�PB2Q2J2�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��1.4176�B
�@N��0.4 �Ƃ��CP��1.4176�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C�ύt�_�iE2�j�ƍœK�_�iJ2�j�͈قȂ�B�������C�u��p���ʂŐ�����O���s�o�ϐ��v�ƁC�u���p���ʂŐ�����O���o�ϐ��i���j�v�����݂���ɂ�������炸�C���҂����܂��ܓ���̐�������ɗ����邽�߂ɁC�ύt���iEE2�j�ƍœK���iNJ2�j�͈�v����35�j�B����̂ɁC�O�҂�}������ېł̒�����C��҂𑣐i����⏕���̌�t�͕s�v�ƂȂ�B
�Ȃ��C���b�Z�E�t�F�[���s��ɂ�����炳��鏃�Љ�։v�̍ő�l�́C�u�}�`G2Q2J2B�f�̖ʐρ|�}�`PB2A�fG2�̖ʐρv�i0.2488�j�ɓ������B�܂��C�_F2�͕s����ȋύt�_�ɂ�����C�_G2�͏��Љ�։v���ɏ��ɂ���_�ɂ�����B
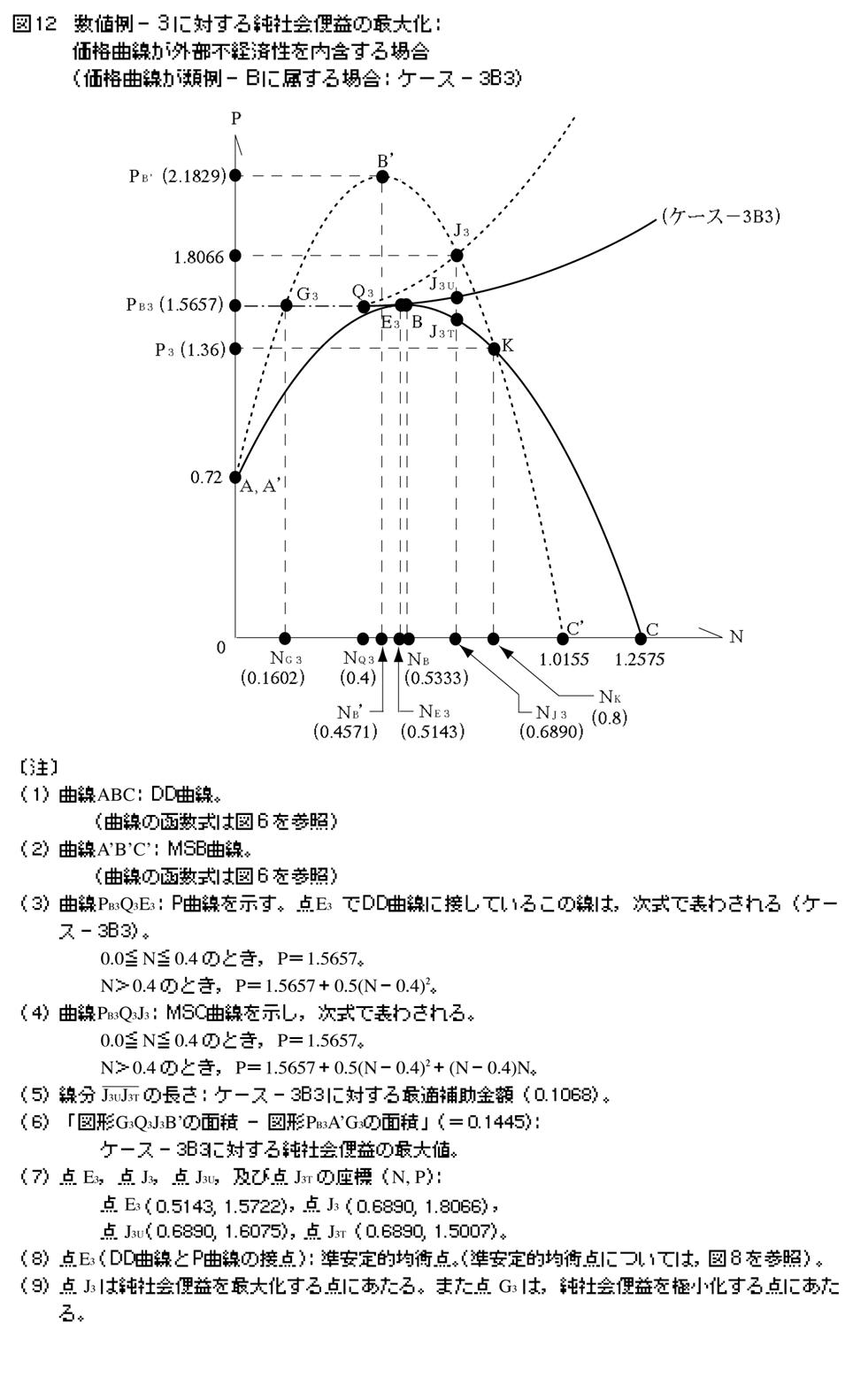
�S�|�S�|�X�@�P�[�X�|3B3
�}12�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�PB3Q3E3��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��1.5657�B
�@N��0.4 �̂Ƃ��CP��1.5657�{0.5�iN�|0.4�j2�B
���̂Ƃ��C���E�Љ��p�Ȑ�PB3Q3J3�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��1.5657�B
�@N��0.4 �̂Ƃ��CP��1.5657�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C�ύt�_�iE3�j�ƍœK�_�iJ3�j�͈قȂ�C�ύt���iNE3�j�ƍœK���iNJ3�j�͘�������B���̂Ƃ��C�O�҂͌�҂����������C�u���p���ʂŐ�����O���o�ϐ��i���j�v�́C�u��p���ʂŐ�����O���s�o�ϐ��v�𗽂��ł���B����āC���Љ�։v���ő剻�����邽�߂ɂ́C�⏕���̌�t�ɋ���ύt���̒l���œK���̒l�ɂ܂ň����グ�邱�Ƃ��K�v�ƂȂ�B���̍ۂɓK�p���ׂ��œK�⏕���z�͐���J3UJ3T�̒����i0.1068�j�ɓ������C�����鏃�Љ�։v�̍ő�l�́C�u�}�`G3Q3J3B�f�̖ʐρ|�}�`PB3A�fG3�̖ʐρv�i0.1445�j�ɓ������B
�Ȃ��C���o���v�Ȑ��Ɣ�p�Ȑ��̐ړ_�ɂ�����ύt�_�iE3�j�́C������I�ύt�_�i������ύt�_�ɂ��ẮC��4�|4�|5�߂��Q�Ƃ��ꂽ���j�ƂȂ�B�܂��C�_G3�́C���Љ�։v���ɏ��ɂ���_�ɂ�����B
�y59�Łz
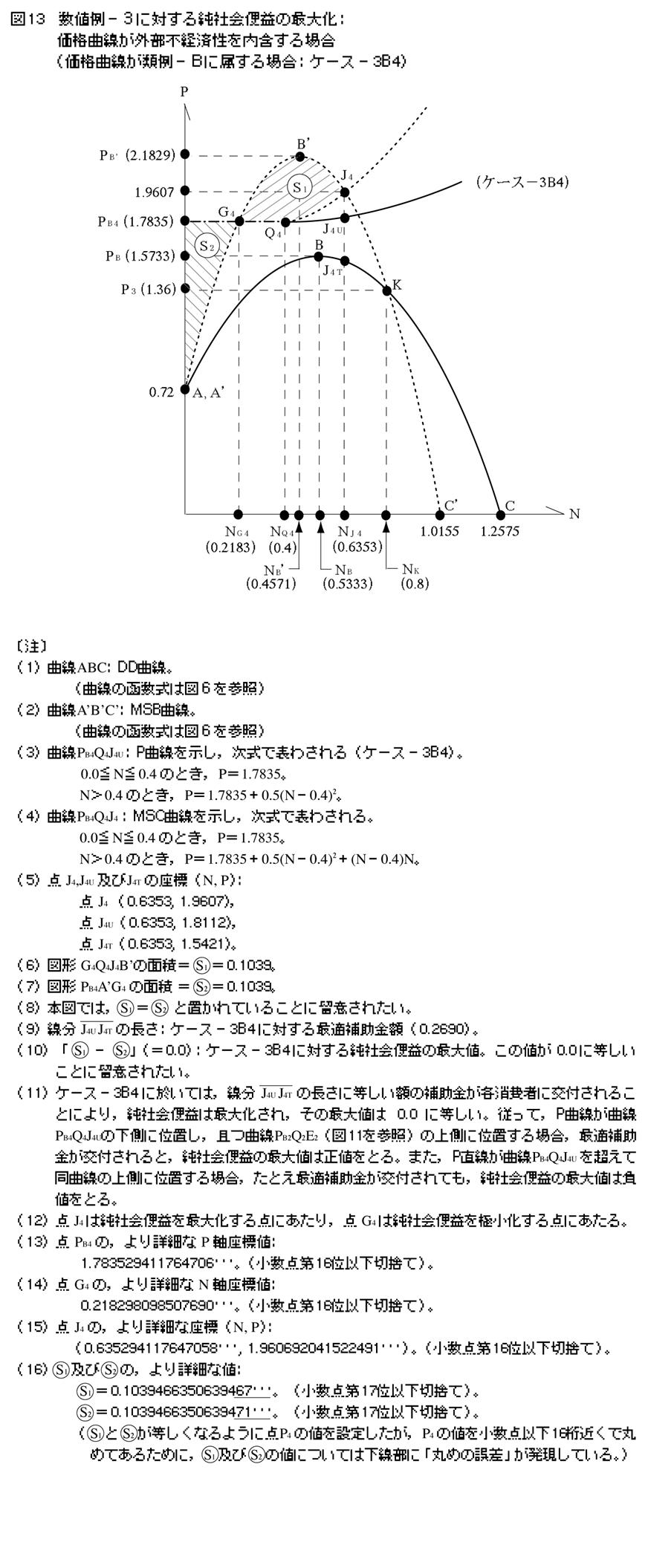
4�|4�|10�@�P�[�X�|3B4
�}13�������悤�ɁC�����ŕ\�킳��鉿�i�Ȑ�PB4Q4J4U��ݒ肷��B
�@0.0��N��0.4 �̂Ƃ��CP��1.7835�B
�@N��0.4 �̂Ƃ��CP��1.7835�{0.5�iN�|0.4�j2�B
���̂Ƃ��C���E�Љ��p�Ȑ�PB4Q4J4�͎����ŕ\�킳���B
�@0.0��N��0.4 �̂Ƃ��CP��1.7835�B
�@N��0.4 �̂Ƃ��CP��1.7835�{0.5�iN�|0.4�j2�{�iN�|0.4�jN�B
�}���疾���炩�Ȃ悤�ɖ{�P�[�X�̏ꍇ�C�P�[�X�|3A6�Ɠ��l�ɁC���i�Ȑ�����ɓ��o���v�Ȑ��̏㑤�Ɉʒu����B����̂ɁC�ύt�_�͑��݂��Ȃ��B�������œK�_�iJ4�j�͑��݂���̂ŁC����J4UJ4T�̒����i0.2690�j�ɓ������œK�⏕���z����肷�邱�Ƃ��ł���B����āC���⏕���z�̌�t�ɂ��C�u���p���ʂŐ�����O���o�ϐ��i���j�v�������ꏃ�Љ�։v���ő剻�����B���̂Ƃ��̍ő�l�́C�u�}�`G4Q4J4B�f�̖ʐρ|�}�`PB4A�fG4�̖ʐρv�i0.0�j�ɓ������B
�ȏ�̎w�E�ƃP�[�X�|3B2�y��3B3�Ř_�������e���čl����Ɩ����炩�Ȃ悤�ɁC�Ȑ�PB4Q4J4U�̌`�Ԃ�ێ��������i�Ȑ����C���i�Ȑ�PB2Q2E2�i�P�[�X�|3B2�j�̏㑤�Ɉʒu���C���y60�Łz���i�Ȑ�PB4Q4J4U�i�{�P�[�X�j�̉����Ɉʒu����ꍇ�C�œK�Ȋz�̕⏕����t�ɋ��蓾���鏃�Љ�։v�̍ő�l�͐��l�������B�����C��q�̌`�Ԃ�ێ��������i�Ȑ����C���i�Ȑ�PB4Q4J4U�̏㑤�Ɉʒu���C�����E�Љ�։v�Ȑ��̒��_B�f���Ȃ��ꍇ�ɂ́C���Ƃ��œK�_�ɑΉ�����⏕������t����Ă��C���̂Ƃ��ɓ����鏃�Љ�։v�̍ő�l�͕��l�������B����Ă��̏ꍇ�C���Љ�։v�̍ő�l�͒[�_���iN��0.0�̂Ƃ��ő�l0.0�j�ƂȂ�B�܂��C��q�̌`�Ԃ�ێ��������i�Ȑ����_B�f�̏㑤�Ɉʒu����ꍇ�C���Љ�։v�̒l��N�l�̌��������ƂȂ�̂ŁC�ő�l�͓������[�_���ƂȂ�N��0.0�̂Ƃ�0.0�������B
�y61�Łz
�S�@������
�O�e�i���v�Ȗʕ��́q����1�r�j�y�і{�e�i���v�Ȗʕ��́q����2�r�j�Ŏ��݂��O���o�ϐ��̍l�@�ł́C�i1�j���v�Ȗʂ̍\�z�Ɠ��Ȗʂ��狁�߂��铱�o���v�Ȑ��ƌ��E�Љ�։v�Ȑ��C���тɁi2�j���Љ�։v���ő剻����œK���v�����C�œK�ېŊz�y�эœK�⏕���z�ɁC�����Ə������Ă��B����������܂ł̈�A�̍l�@�́C��̓I�Ȑ��l���ݒ肵�Đ}���I�ɊO���o�ϐ��̓������тɗ��������⏕������݂̍����T�낤�Ƃ�����̂ɉ߂����C����̉ۑ�Ƃ��Ă���ʉ����ꂽ�l�@�̓W�J�������B
�����C���v�Ȗʕ��͓I�A�v���[�`����āC�u�O���o�ϐ��i���y�ѕ��j����܂�����v�Ȗʂ��狁�߂��铱�o���v�Ȑ��ƌ��E�Љ�։v�Ȑ�������������v�\���ɖڂ����鎎�s�́C�u���v�Ȑ��ƌ��E�Љ�։v�Ȑ��͒ʏ�E������̋Ȑ��Ō݂��Ɉ�v����v�Ƃ����`���I�Ȍo�ϊw�̎v�l�I�g�g�ɁC�����₩�Ȃ�����V���Ȍ��n������邩������Ȃ��B
������ǎҏ��������݂̂Ȃ���ᔻ�����C���v�Ȗʕ��͓I�A�v���[�`���L���錇�_����v�𒍈Ӑ[���ᖡ����Ɠ����ɁC���v�Ȗʕ��͓I�A�v���[�`�̍X�Ȃ�ᖡ�Ɖ��p36�j�ɐS���������B�Ȃ����e�ł́C�O�e�y�і{�e�܂��C���v�Ȗʂ̊T�O�ƑΏƂ����Ȃ���C�����Ȗʂ̊T�O�ɐG��Ă݂����B
��L
�{�e�ł́C�M�҂炪�����Ői�߂Ă������v�ȖʂɊւ���l�@�̓��e���C�}���I�ɘ_�����B���̎��݂ɉ����āC���_�I���͂͂��Ƃ��Mathematica 5.1 (Wolfram Reserch Inc., 2004) �ɋ����}��Ƃɑ��đO�e�Ɠ��l�ɑ��M�ҁi��C�j���S���������͌����ł���C���̘J�ɑ����M�ҁi�쓈�j�y�ё�O�M�ҁi�����j�͓��L���Ďӈӂ�\����B
 f
f
�y67�Łz
[�Q�l����]
��ΑוF�i2005�j[�ҁE���E�Ė�]�C���E��p���i�`�������̌����C�������[�C�����B
�쓈�C�F�i1975�j�C�u�s�s���̌o�ϊw�i�}���I���́j�v�C�V�s�s�C��29��3���C�s�s�v�拦��C �����C4-14�ŁB
�쓈�C�F�C�����K�V�C��C����C�������ގq�i2007�j�C�u�O���o�ϐ��̍l�@�i���v�Ȗʕ��́q����1�r�j�\ ���v�Ȗʂ��狁�߂��铱�o���v�Ȑ��ƌ��E�Љ�։v�Ȑ� �\�v�C�w�K�@��w�o�Ϙ_�W�C��44����3���C�w�K�@��w�C�����C203-262�ŁB
Buchanan, J.M., 1965, �gAn Economic Theory of Clubs,�h Economica, Vol.32, No.125, pp.1-14.
Else, P.K., 1981, �gA Reformulation of the Theory of Optimal Congestion Taxes,�h Journal of Transport Economics and Policy, Vol.15, pp.217-232.
Else, P.K., 1982, �gA Reformulation of the Theory of Optimal Congestion Taxes: A
Rejoinder,�h Journal of Transport
Economics and Policy, Vol.16, pp.299-304.
Kawashima, T., 1980, �gOptimal Congestion Tax of Expressway:
A.A.Walters Re-examined, P.K.Else Re-appraised, and Demand-surface Paradigms
Re-considered,�h Gakushuin Economic Papers, Vol.25, No.2,
Kawashima, T., 1990, �gOptimum Level of Traffic Congestion Taxes: An
Outgrowth of Else�fs
Approach,�h New Frontiers in Regional
Science: Essays in Honour of Walter Isard, Volume
1, Edited by M.Chatterji and R.E.Kuenne, MacMillan,
Kawashima, T. and R. Samata, 2004, �gCase and Theory of NGO Volunteer Activities:
International Grassroots Cooperative Programmes by GONGOVA for Uplander
Villages in
Nash, C. A., 1982, A Reformulation of the Theory of Optimal
Congestion Taxes: A Comment,�h Journal of
Transport Economics and Policy, Vol.16, pp.295-299.
Wolfram Research Inc., 2004, Mathematica
5.1 (computer application software),
Walters, A. A., 1961, �gThe Theory and Measurement of Private and
Social Cost of Highwasy Congestion,�h Econometrica, Vol.29, pp.676-699.