【83頁】
金融工学におけるタームストラクチャーの視覚的教授法
要旨
金融工学における重要概念として,金利のタームストラクチャーモデルがあるが,その数学的プロセスは学生にとって理解が難しく,ここで金融工学自体に挫折してしまう学生も少なくないと言える。本稿では,金利のタームストラクチャーモデルに関連する各種の概念,スポットレート,デュレーション,イミュニゼーションなどを,グラフィクスを用いて学生に教授する方法について報告する。これにより,タームストラクチャーモデルにおけるデュレーションの偏導関数の意味,再帰的な債券価格の求め方,などの理解が容易となる。我々は常々,数学教育におけるグラフィクス活用の有効性を主張しているが,本稿ではタームストラクチャーモデルの,ビジュアルアプローチに基づく教案を提示する。内容は実際に我々がMapleを用いて講義した経験に基づくものである。代数学的アプローチだけでは理解困難な場合でも,ビジュアルなアプローチによる説明で教えると,学習における理解度が向上すると期待される。また,本稿では,グラフィクスを学生自身に描かせることによる効用も論じる。グラフィクスを描くことで,数式の詳細部を認識する,グラフィクスの詳細部を観察する,という作業を繰り返すことになるので,結果として数学的プロセスの理解が深まる。
1. 始めに
金融工学における重要概念として,金利のタームストラクチャーモデル(term
structure model of interest rates)がある。タームストラクチャーは,債券数学を理解するためには必須の概念と言えるが,一般に,タームストラクチャーのモデルを理解することは難しいと言われている。
タームストラクチャーモデルを導入する以前のモデルでは,満期利回りを,期間中一定値とする。このモデルを,本稿では,満期利回り固定モデルと呼ぶことにする。それに対して,タームストラクチャーモデルでは,任意の時点で,全ての満期日に対してある金利が決まる。この金利は,スポットレートと呼ばれ,満期までの時間の関数として表される。スポットレートを用いることで,将来のキャッシュフローの現在価値も計算可能となり,確定利付き債券の価格も計算できる。満期利回り固定モデルをタームストラクチャーモデルに拡張したことにより,【84頁】確定利付き債券の価格の値も,満期までの時間に依存することになり,より現実的になる。しかしながら,このモデル拡張を理解することが,学生にとって簡単ではない。
我々は既に満期利回り固定モデルにおいて,視覚的教授法を使ってデュレーション,コンベキシティ,イミュニゼーションなどの概念を視覚的に説明してきた[1]。そこでは,債券価格の関数を4個の独立変数をもつ多変数関数とみなし,3次元グラフィクスによって,各変数間の関係,つまりそれは偏微分の偏導関数に相当する関係として,視覚的に説明した。加えて,イミュニゼーションにおけるテイラー展開による関数近似の様子を,視覚的に表示した。これにより,債務の現在価値と,ポートフォリオの価格が一次近似,二次近似と精度を上げるにつれて,どのように接近するか,また,一度金利変動が起こると,もはやイミュニゼーションの効果は薄れる可能性があることなどを,視覚的に分かりやすく説明した。
“金利のタームストラクチャー”の日本語訳は,“金利の期間構造”が一般的であるが,本稿を含めた著者らの論文では,“タームストラクチャー”と呼ぶこととする。理由は,金融工学はアメリカで生まれた学問なので,金融工学の本は英語のものが多いからである。学生には,最新の英語のテキストを読めるようになってほしいので,それらを読むときの障壁が軽減されるようにと,考えてのことである。
本稿では,金利のタームストラクチャーモデルを視覚的に教授する方法について述べる。
第2節は,タームストラクチャーモデルを教授する際の指導案のポイントを示す。最重要課題は,スポットレートカーブの平行シフトを理解させることである。第3節では,イミュニゼーションの過程の,タームストラクチャーモデルへの拡張を,どのように講義するか,その方法について論じる。第4節は,スポットレートカーブが平行シフトした場合の債券価格の変動についての視覚的教授法を述べる。第5節では,ビジュアルアプローチの学習効果について考察する。最終節はまとめである。
2.タームストラクチャーとスポットレートカーブ
本節では,金利のタームストラクチャーモデルを教える際の教案作成のポイントを説明する。始めに,教師は,どこで学生が躓くのかを理解することが必要となる。
タームストラクチャーのテキストとしては,LuenbergerによるInvestment Science[2,
3]が世界的に有名であり広く使われているので,我々もそれを教案のベースとした。その他にも,カラーグラフィクスが豊富なCornettらによる教科書[4],分かりやすい説明のBazらによる良い教科書[5]などがある。日本語の教科書としては,数学的定義が厳密な木島の著作がある[6]。
タームストラクチャーを理解する際に,学生にとって最も難解な部分は以下の箇所であろう。いずれも,満期利回り固定モデルから,スポットレートカーブ導入によるタームストラクチャーモデルへの,モデル拡張のプロセス部に関わっている。
(1) 満期利回り固定モデルにおいては,満期利回りは常に固定であるという仮定のもと,内部収益率IRRの計算方法を使って,満期利回りを計算する。にもかかわらず,現実には満期利回りが変動する。
(2) IRRを固定する,とした仮定は,何が現実的でなかったのか,満期利回りモデルの欠点が答えられない。
【85頁】
(3) タームストラクチャーモデルにおいては,スポットレートカーブは垂直軸方向に,平行シフトする。つまり期間全体に渡り,固定量Δrだけ,変動する。デュレーションの定義は,このΔrに対する債券価格の変化率であるが,デュレーションの計算の際に,この導関数の意味がよく分からない。
(1)において,満期利回りが変動することは理解しても,満期利回り固定モデルの何が現実的でなかったのか,学生が明言できない場合がある。
上記3つのポイントとして,学生が疑問に思う個所を具体的に示したが,それを集約すると,デュレーションの導関数の意味が理解できない,ということになる。満期利回り固定モデルにおいてIRRが固定であるという意味,および,IRR の平行シフトの意味が,学生はなかなかイメージできない。IRR固定とは,何の変数に対して固定なのか,スポットレートカーブの平行シフトと同じ座標系の中で,IRR固定ということを,同時に描画するとどのようになるのかが,頭の中で描けない。具体的な数式を見ても,両モデルにおいて,ΔrあるいはΔλの変動がでてくるが,それらの差異を,同じ座標系の中で同時に描けない。
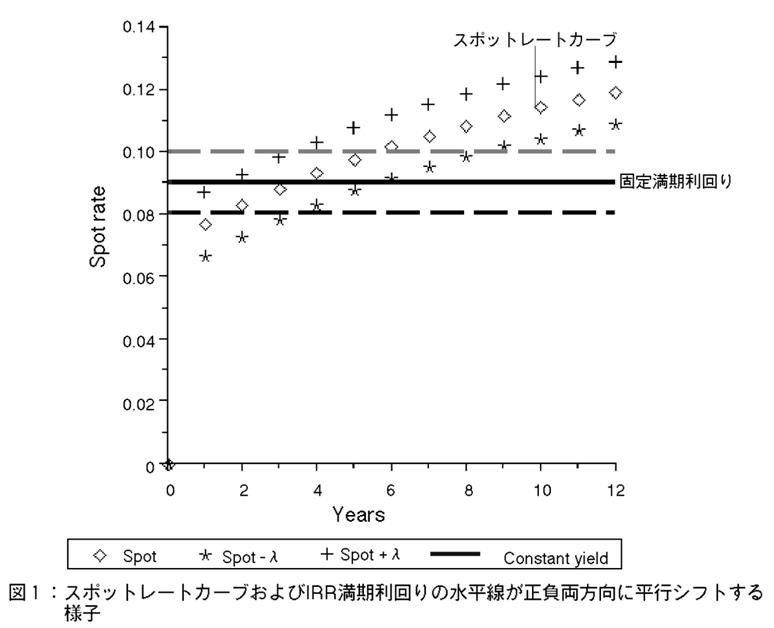
これらに対する教授法としては,グラフィクスを使って説明することが最良策である。図1に両者の差異を図示した。上述した学生の3つの疑問に答える基本は,この図1である。まず,スポットレートカーブと,固定の満期利回りの関係を図で理解させることが重要である。
【86頁】
この図1を使って,学生に教えるべきポイントは以下の通り。
●満期利回り固定モデルでは,満期利回りは横軸(時間あるいは満期)に対して一定値をとる。それは水平線を描く。
●スポットレートカーブは,時間(満期)に依存する関数である。
●スポットレートカーブは,利回りの時間依存関数としての一般形であり,時間に関して定数をとった特殊ケースが,満期利回り固定モデルである。
●スポットレートカーブの平行シフトとは,任意の時間に関するスポットレートが,同じ量Δrだけ,上下に平行移動することである。図1では,オリジナルカーブを中心に,上下にシフトした様子を示している。
図1では,満期利回り固定モデルにより定義された,3本の満期利回り直線が,3本の水平線として描かれている。中央の直線が,オリジナルな満期利回り直線であり,上下の2本が,Δrだけ利回りが変動した場合に対応している。
満期利回り固定モデルを教えていると,「IRRとして,満期利回りが固定であることに疑問をもつ」学生が出てくる。ここに疑問をもつ学生は,そこまでの理論を理解している学生であると言える。そうした場合は,その学生の疑問への回答として,「満期利回りは,債券のクーポンの再投資の際に,同じ利回りで再投資可能であるという仮定に基づいている。しかし,この仮定は現実的ではない。そのため,より現実的なモデルとして,タームストラクチャーモデルが生まれた。実際に,再投資の利回りがIRRの値を取れるか否かは,その時の現実の金利に依存するので予測不能である。そこで,改善策として,利回りは時間に依存するというタームストラクチャーモデルを導入した。」と,学生に説明する。
こうした説明の際,図1のように,2つのモデルにおけるΔrを同時に描画したグラフィクスは,学生の理解を大いに助けてくれる。同時に描画する点がポイントと言える。
3. 拡張されたイミュニゼーション・プロセス
本節では,タームストラクチャーモデルにおいて,イミュニゼーション・プロセスがどのように拡張されるのかを講義する,視覚的教授法を示す。用語,概念についてはLuenbergerのテキストInvestment Scienceを参照して頂きたい。
確定利付き債券の価格は,以下のNPV(net present value)の公式を適応することで計算される。
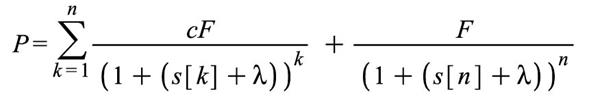
この計算式では,複利計算は1年ごと,つまりP.A. (per annually)で行われていると,している。P は債券価格,s[k]は時間kにおけるスポットレート, cはクーポン率, Fは額面,λはIRRを表している。この価格関数より,デュレーションが求められる。ピュア・デュレーションDは以下の式で定義される。
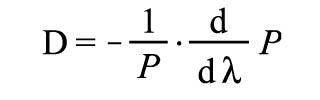
【87頁】
上式に値を代入して,P.A.で複利計算した場合,ピュア・デュレーションは以下のようになる。
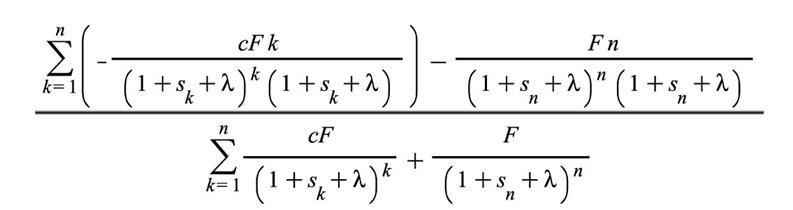
上記の表記では,スポットレートの添え字kが,k年後を示している。
こうして,デュレーションが計算できたならば,イミュニゼーション・プロセスをタームストラクチャーモデルにおいて定義することが可能となる。イミュニゼーションでは,債務とポートフォリオの(1)現在価値,と(2)デュレーションの値を合わせる,からである。
以下では,Luenbergerのテキスト中の Example 4-8[2] を例に用いて,我々の教授法を説明する。この問題は,債務に対して,2種類の確定利付き債券でポートフォリオを組む問題である。この文章題は以下のように要約できる。
Given
Data:
◇債務: $1000000,期間は5年
◇複利計算方式: P.A.
◇スポットレートカーブ: [7.67,
8.27, 8.81, 9.31, 9.75, 10.16, 10.52, 10.85, 11.15, 11.42, 11.67, 11.89]
◇債券1: 12年もの,クーポン率 6%,価格 $65.95
◇債券2: 5年もの,クーポン率 10%,価格 $101.66
◇額面: $100
Unknown:
◇スポットレートの平行シフトに対して,債券1と2でポートフォリオを組んでイミュニゼーションする際の,債券1と債券2の其々の購入量
デュレーションとして,Luengerberは準修正デュレーション(quasi-modified duration)を使っているが[2],これはピュア・デュレーションの値と等しくなる。我々は,イミュニゼーションの計算にはピュア・デュレーションの定義式を使うように学生に指導している。
ピュア・デュレーションの定義式には指数関数の偏微分が含まれており,計算が複雑であるので,数学ソフトウェアを使ったほうがよい。一般にタームストラクチャーに関する計算は複雑であるので,数学ソフトウェアは演習に必須であると我々は考える。理由としては,手計算に集中すると,議論の本筋から離れてしまうこと,および,そもそも金融工学の数学は複雑で,手計算の範疇を超えていること,があげられる。我々は演習では,Mapleを使っている。
一方では,数学ソフトウェアに過度の依存をせぬよう注意している。機械任せの機械カタギ(1)【88頁】になって,学生自身が計算結果の正当性チェックができなくなるようではいけない。我々は,視覚による計算の正当性チェックを推奨している。つまり,グラフィクスに描いてみることで,自分のもっている知識と照合しチェックを行うのである。何かグラフィクスに異変を感じれば,精査することで,入力ミスなどの誤りを発見できる。
デュレーションの定義は,満期利回り固定モデルにおいては,マコーレーのデュレーションと修正デュレーションがあり,タームストラクチャーモデルにおいては,フィッシャーワイルのデュレーションと準修正デュレーションがあり,ピュア・デュレーションを含めると5個のバージョンがある。よって学生は混乱しがちである。我々の講義では,ピュア・デュレーションを中心に教える。他のバージョンは,モデルの違いから来る派生的なものとして捉えるように指導している。
図2,3に,イミュニゼーションの結果のグラフィクスを示した。図2が現在価値,図3がデュレーションである。
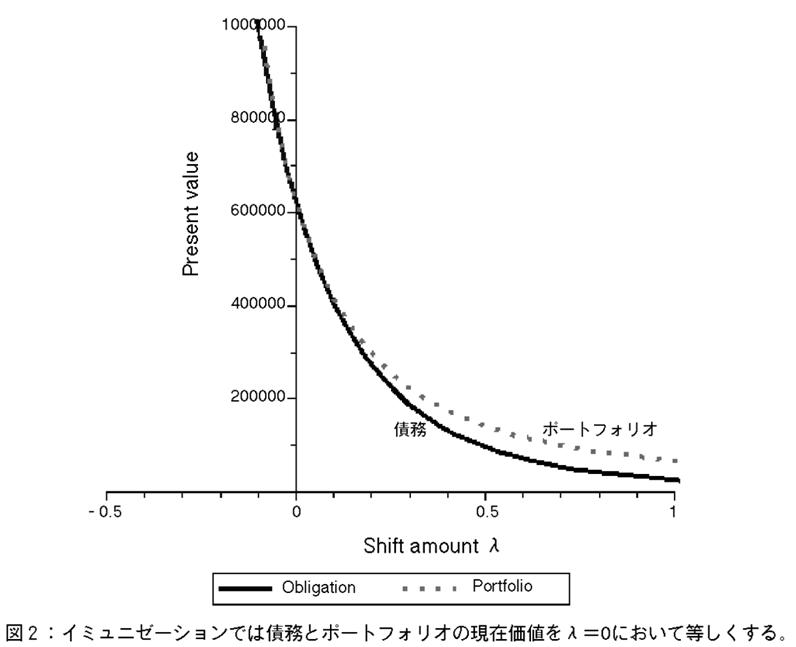
ポートフォリオの価格は,スポットレートカーブの平行シフトが起こっても,債務の現在価値の変動に追従できるようになっている。図2を見ると,シフト量λがゼロの場合,ポートフォリオの価格が債務の現在価値に等しくなっていること,および,その現在価値の点における接線が一致していることが視覚的に確認できる。
【89頁】
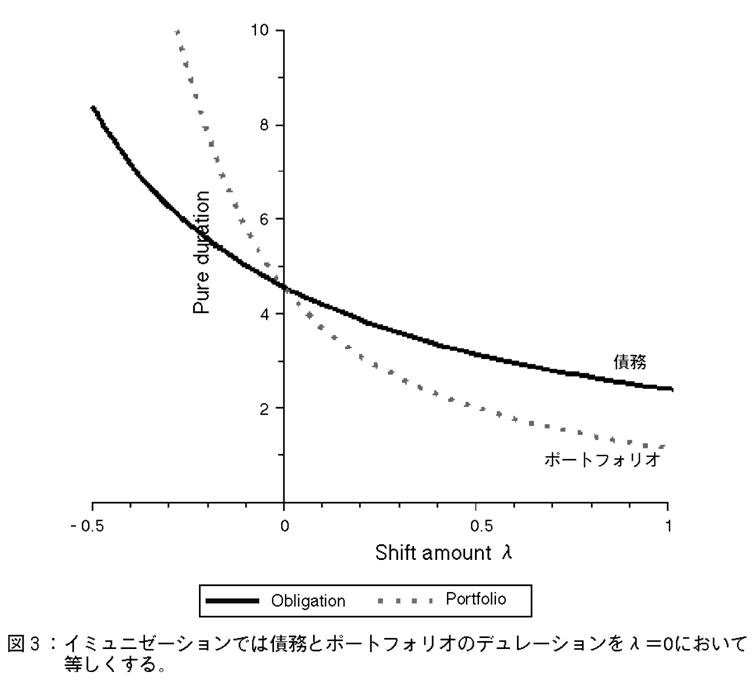
図3を見ると,シフト量λがゼロの時,両者のピュア・デュレーション値が等しいことが視覚的にわかる。学生はこうしたグラフィクスを見ることにより,拡張されたイミュニゼーション・プロセスを容易に理解できるようになる。
4. 平行シフトに対する債券価格
本節では,タームストラクチャーモデルにおいて,スポットレートカーブが平行シフトした場合の債券価格への影響を見る。債券は前節までと同様に,確定利付き債券とする。
タームストラクチャーモデルにおける,債券価格の計算方法は,“running
present value”と呼ばれる,漸化式からの帰納的計算方式である[2,
3]. ここで用いられる漸化式は以下の通り。
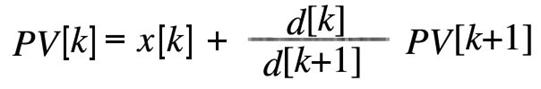
PV[k], d[k]は時間kにおける現在価値と,ディスカウントファクターを表す。x[k]は時間kにおけるキャッシュフローである。
帰納的計算方式では,最後のキャッシュフローから始めて,時間的に逆方向に,再帰的に現在価値を計算していく。そして,現時点t=0において,最終的な現在価値を得る。
【90頁】
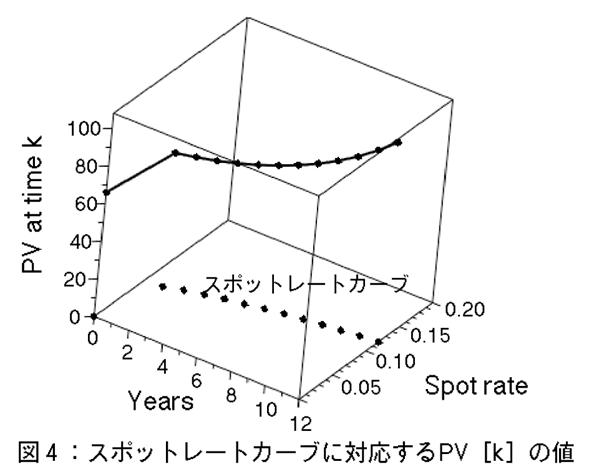
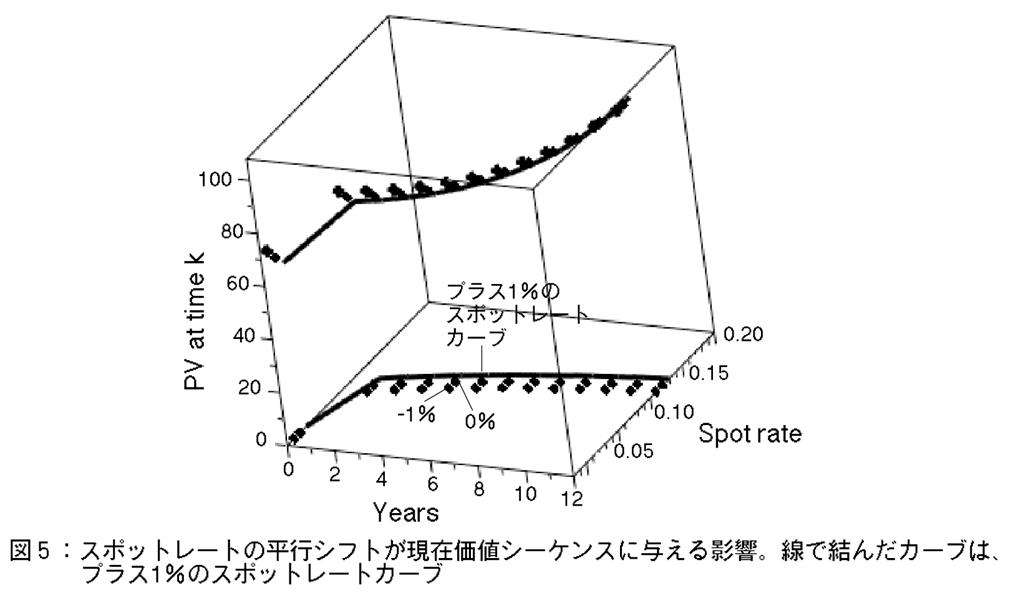
この計算方法はよく使われる方法であるが,時間 t=k(年)における現在価値PVと,スポットレートカーブの関係が,学生には分かりにくいようである。そこで我々は,図4と5に示すような3-Dグラフィクスで,その関係を図示した。このグラフィクスでは,以下のような仕様の債券を用いた。
◇クーポン率: 6%
◇スポットレート: 前節の例,Example4-8と同じとする
◇ 額面: $100
◇満期: 12 年 (P.A.)
【91頁】
計算は, PV[k]
(k=12 years) から始める。次に, PV[k]の列が,逐次的かつ,t=0に向かって逆向きに時間を遡る方向で計算されていく。最後に, PV[0] が計算される。現時点t=0におけるスポットレートは0とした。
我々は,図4で,このPV列の値を,時間~スポットレートの2次元平面の上に,3番目の次元として描いた。授業では,図4を見せながら,学生に以下の説明をする[3]。「各時点においては,その時点のキャッシュフローと,その時点のスポットレートしかしか知らされていない。バケツリレー的に渡されるデータは,隣り合う時点の現在価値PVと,隣り合う時点でのスポットレートのみである。」漸化式による離散的なシーケンスの計算に慣れていない学生にとって,図4は理解の助けになると考えられる。
次にスポットレートカーブの平行シフトの影響を見るための図として,図5,6,7を学生に示す。これらはスポットレートカーブがオリジナルカーブを中心に,1%上下にシフトした様子を示している。線で結んだカーブは,プラス1%のスポットレートカーブである。
図5の中で,現時点t=0の平面に注目する。この平面上には,異なる3つの平行シフト量(+1%,
0%, -1%)に対する,現在価値(債券価格)の値がプロットされる(図6参照)。
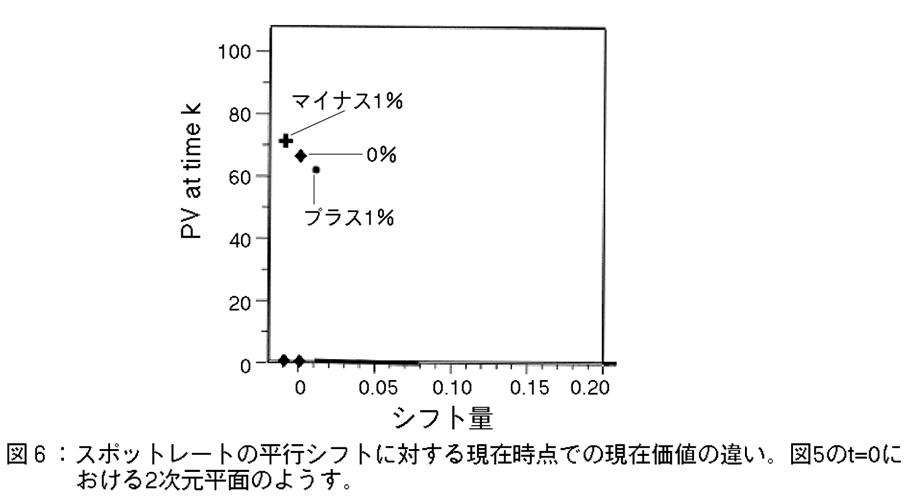
この平面上の点を補完してカーブにすると,見なれた債券価格と満期利回りの関数グラフとなる。シフト量が増えるに従い,債券価格が下がる減少関数である。ここでは,グラフィクスが煩雑になるためプロット数を3つにしているが,より多くの点をプロットすることで,カーブが減少しているが明確になる。
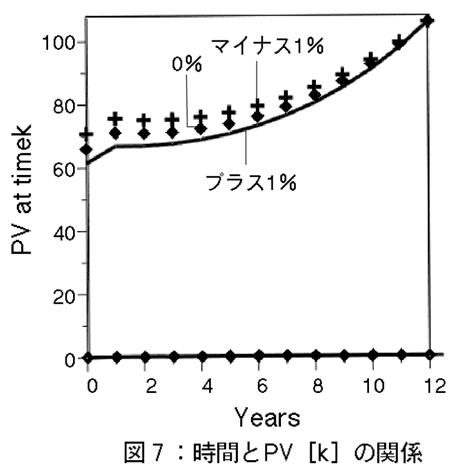
図7は,時間と債券価格の間の関係を3種類の平行シフト量についてプロットしたグラフィクスである。線で結んだカーブは,プラス1%のスポットレートカーブである。この図より,t=0に近づくにつれて,現在価値が下がる様子が見られる。また,平行シフト量がプラスの方が,債券価格 PV[0]が小さいという様子が見られる。
一般的に見て,スポットレートカーブの平行シフトが,現在価値の列に与える影響を,学生に理解させることは難しいと言える。しかしながら,本節で述べたような各種のグラフィクスを描かせることで,理解が容易になると考える。
【92頁】
5 ビジュアルアプローチの効果
本節では,タームストラクチャーモデルの講義から得た,筆者らのビジュアルアプローチの学習効果について考察する。我々の教授法の特徴は,ビジュアルアプローチである。それは,数学教育におけるIT活用の最も特長的なアプローチと言える。
視覚的説明は,千の言葉よりも分かりやすく概念を学生に伝えることができる。しかしながら一般に,金融工学のテキストにはグラフィクスが少ないと我々は感じる。例外はMathematicaを使って金融工学を説明したテキストであるが[7-9],その対象はデリバティブが殆どであり,債券数学を対象とした本においては,やはりグラフィクスは少ないと感じる。特に多変数関数の3次元グラフィクスは少ない,と感じる。こうした状況は改善していくべきと,我々は考える。
経済および経営数学の教科書に関しても,日本は欧米に比較して,グラフィクスを多用した教科書が少ないように感じる。多変数関数の3次元グラフィクスを多用した教科書として拙著があるが[10],その数はまだまだ少ない。その理由はコストの問題から来る,IT環境整備および数学ソフトウェアの導入率の低さであろう。数学ソフトウェアを導入し,数学テキストを執筆する教員が日本でも今後,増えることを期待する。
グラフィクスのもうひとつの活用法は学生自身にグラフィクスを描かせることである。従来の我々の視覚的教授法においては,描画させることの効果について,我々自身も気づいていなかった。しかしながら,債券数学のタームストラクチャーモデルのように複雑化した離散的多変数関数を扱うようになると,描くことで理解する,という利点が顕著になった。
グラフィクスを描くためには,まず,数式を正しく入力することが必要である。入力の際,見間違えなどによりミスをすると,グラフィクスが予想と違うので,すぐにミスが発見できる。例えば,Σに関する部分がどこまでの範囲か,見極めるために,学生は熱心に数式を眺めるようになる。また,テキストに描かれていないパラメータの組み合わせや,ドメインにおいて,グラフィクスを多数描いてみることにより,関数形の詳細が分かるようになる。グラフィクス【93頁】を描くことで認識の誤りが訂正され,また,描けたグラフィクスを見ることで,関数形への認識が深まる。
自分でグラフィクスを描くことは,このように,良い方向への学習発展スパイラルとなる。これは我々だけの主張ではなく,多くの数学教育者が気づいている。例えば,この方針に基づいたMathematicaによる数学の本として「試して分かる高校数学」[11]がある。
今後は,グラフィクスを見ることによる効果だけではなく,グラフィクスを数学ソフトウェアで描画することの教育的効果についても言及していきたい。
6 まとめ
本稿では,債券数学を理解する上で避けられない重要概念であるタームストラクチャーモデルを,視覚的に教授する方法を述べた。
タームストラクチャーモデルにおいては,以下の概念が重要となる。
(1) スポットレートカーブ
(2) デュレーションの拡張
(3) イミュニゼーション・プロセスの拡張
(4) スポットレートカーブの平行シフトが,現在価値に与える影響
特に,デュレーションを求める計算においては偏微分を行う必要があり,何について偏微分するのかを理解させることが難しい。スポットレートカーブの平行シフト量について偏微分する,という関係が頭の中で図に描けないのである。そうした場合に,グラフィクスによる説明は学習効果が高い。学生はグラフィクスを描きかつ見ることで,以下の事柄を容易に理解可能となるであろう。
(1) 満期利回りは一定であるが,何に対して一定であるのか?(答えは時間)
(2) IRRとして計算された満期利回りは,スポットレートカーブとどのような関係にあるのか?(答えは図1)
(3) スポットレートカーブの平行シフトとはどういうことなのか,またそれにより債券価格にどのような影響を与えるのか?(答えは図5および6)
ビジュアルアプローチにおける「見て分かる」グラフィクスの効用については,オージンガー教授も同様のことを述べておられる。彼女は世界で初めてローレンツ変換をグラフィクスによって表した[12]。それまで物理学者もローレンツ変換の詳細については漠然としたイメージしかなかったが,このグラフィクスにより細部が明らかになった。[12]の講演ビデオの中でこの複雑かつ美しいグラフィクスが見ることができる。オージンガー教授とのディスカッションにより,我々はビジュアルアプローチの正しさを改めて認識し,意欲を新たにした次第である。
数学ソフトウェアによるグラフィクスを体験すると,確かに学習効率が向上する。これは筆者らの数学講義体験からも強く感じられる。問題はコンピュータ環境整備にコストがかかることである。しかしながら,グラフィクスを描かせる演習は効果があるので,学生には,もっとグラフィクスを描いてもらい,特に3次元グラフィクスを多数描いてもらうことで,関数にお【94頁】ける変数間の関係の詳細を調べるように指導していきたい。また,この描かせるという演習方式も広く普及させていきたいと考える。
我々は今後も,債券数学,金融工学の数学の教授法において,関数をグラフィクスとして見せて説明するビジュアルアプローチとともに,学生自身に描画させるという教授法を発展させていきたい。