【263頁】
金融工学数学のためのグラフィクス教材データベース
――Bond Mathematics by Graphics――
金融工学数学のためのグラフィクス教材のデータベースのWEB サイトを立ち上げたので報告する。金融工学数学は難しいと言われるが,数学を理解させるために,グラフィクスの利用は有効であり,その利用により学生の理解度を高めることが可能である。我々は,大学および高校の数学授業において,グラフィクス教材をもっと多く活用してもらうためにこのサイトを開いた。そのため,数式処理ソフトウェアとしては,国内でも普及しているフリーソフトであるMAXIMA(マキシマ)を使った。本稿の目的は,グラフィクス教材作成に際して,ユーザー自身が,パラメータ値を自由に変更でき,ユーザー独自の金融工学数学グラフィクス教材を作成できるようにすることである。教材の内容としては,グラフィクスが効果的に生かせるテーマをとして,ポートフォリオの効率的フロンティア及びイミュニゼーションのテイラー展開描画,住宅ローン,年金の増加関数と減少関数の描画,債券価格の3次元的描画などを選んだ。本稿では,我々が研究中である,債券数学の学習支援システム構想にもふれ,このグラフィクス教材データベースが,その一部であることを説明する。
1. 始めに
我々は,2010年度から,債券数学における学習支援システムの構築を研究している。このシステムの中核として,各種のデータベースが必要となる。債券数学の公式のデータベース,用語データベースであるコーパス,そして,今回のようなグラフィクス教材データベースなどである。
今回,このグラフィクス教材のデータベースのWEB サイトを立ち上げたので報告する1)。サイトのタイトルは,「MAXIMA による経済数学グラフィクス10個:Bond Mathematics by Graphics」である。略してGraphics10と呼ぶ。内容は,金融工学数学,特に債券数学でよく使【264頁】うグラフィクスを10個選んだ。いずれも,実際に大学の講義で使ったものである2)。
このWEB サイト立ち上げは2010年10月19日であり,2010年10月23日の日本経営数学会秋季研究会で,2件の関連論文発表を行い,このサイトのプレ公開のお知らせをした3) 4)。MAXIMAは,世界で広く使われているフリーの数式処理システムである5)。本サイトでは,MAXIMAソースプログラムも提供し,数学の教員の皆様に,自由にグラフィクス教材として使ってもらうことを目的としている。非営利の利用のみ許可している。
プレ公開の間は,ユーザーは,各自のPC にMAXIMA をインストールし,自分のPC 上でMAXIMA を動かす。本稼働後は,MAXIMA をインストールしなくても,我々の提供するサーバ上で動くようにする。Web フォームを通して,パラメータの値を変更し,独自のグラフィクス教材が作成できるようにする。この本稼働は,2011年2月1日を予定している。
第2節,3節は,MAXIMA ソースコードを自分で理解しようとするユーザーのために,書いたものである。第2節では,数式処理プログラム一般に関するプログラミングに関するセオリーを述べる。第3節は,Graphics10の内容である。債券数学が始めてであるユーザーにも分かるように,債券数学の概略を説明しながら,MAXIMA でどのようにプログラムするかを説明した。第4節は,我々が研究している,金融工学の数学教育のための学習支援システム構想のなかで,このグラフィクス教材データベースが占める役割を説明する。最後は,まとめである。
2. 数式処理プログラムに関するセオリー
本節では,Graphics10の内容を読む上で重要となる,数式処理プログラムに関するセオリーを説明する。2個と,数は少ないが,これらはプログラミングの方針であり,MAXIMA に限らず,Maple, Mathematica などの数式処理ソフト一般に適応可能で,適応範囲が広い。我々の作成した「債券数学用公式集」に対して,このセオリーを適用したプログラムを書くことで,論理的な債券数学文章題の解法の考え方ができるようになる。
債券数学用公式集MAXIMA 版は,本稿の付録としたので参照して頂きたい。公式は,等式A = B の形をしており,公式には“F2B” のようにラベルが付けられている。解法に必要な公式を集めて単に連立方程式を解けば,未知数の式あるいは値が求められる
♢ セオリー1:float(solve(ev([連立方程式],Given Data]),[変数]))
連立方程式を解くという,下記の流れをMAXIMA の言語で要約すると,上記のセオリーになる。
【265頁】
1. 公式集から,未知数(Unknown)を求めるために必要な公式を集めて,連立方程式を立てる。
2. 連立方程式を,Given Data の条件下で評価する(evaluate)。
3.連立方程式を解く(solve)。
4.数式を実数に変換する(float などを使う)。
以下に例を示す。
float(solve(ev([F2, F1C], c:0.04, cTimes:1, Times:1, F:100),[Dm, PV]))(途中形)
この例では,公式F2番,および,公式F1C 番という2本の式の連立方程式を,以下の4個のGiven Data の環境下で評価する:c:0.04, cTimes:1, Times:1, F:100。
次に,その連立方程式を,変数に対して解く。上記の例では,[Dm, PV]が,変数集合となっている。最後に,具体的な実数値を求めるために,float を用いる。実は,この例の公式F1Cは微分(偏微分)を含んでいる。微分を含む公式においては,MAXIMA では,微分diff の評価を遅らせる必要があり,カンマを用いて以下のように書く。
F1C2: Dm=−1./PV*’dif(f PV, r);
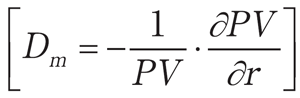
公式を評価して,F1C2というラベルを付けた時点では,diff が評価されないように,’diff()とする。このように評価を遅らせないと,この時点で,dif(f PV, r)が0と評価されてしまうからである。そして,式の中身が代入された時点で,diff を実行し,その後,方程式を解く。
float(solve((ev([F2B, F1C], c:0.04, cTimes:1, Times:1, F:100), diff),[Dm, PV]))(完成形)
♢ セオリー2:floa(t solv(e dif(f 式,変数)=0),[変数]))
金融工学の数学においても最大値,最小値を求める最適化問題は多く出てくる。そこで使われる「極値を求める」数学公式は,微分した結果の導関数をゼロとおき,その式を未知数について解く,というプロセスである。例えば,ポートフォリオ分野において,リスク最小点や,CML(Capital Market Line)のシャープレシオ最大点を求める問題などで,この公式が使われる[1]。以下に,極値を求める公式の適応例を示す。
float(solv(e dif(f riskAC, t)=0, t));
数式処理システムを使い,金融工学数学に関するプログラムを行う場合,この2つのセオリーをベースにすると,プログラムが容易に書ける。以下の節では,その実践として,10個のグラフィクス例を示す。
3. Graphics10の内容
本節では,Graphics10と名付けた10個の金融工学数学に関するグラフィクスを説明する。ここで紹介しているグラフィクスは10個と,数は少ないが,金融工学数学のコアとなるテーマを選んでいるため,パラメータを変更することで,多様なグラフィクス教材を作成することが可【266頁】能となる。また,Maple, Mathematica の数式処理ソフトにおいても,このアプローチによりグラフィクスが作成可能である。実際,我々は,始めはMaple でこれらを作成し,それをMAXIMA に翻訳した。
我々の作成した「債券数学用公式集」と,前節で述べた数式処理プログラムに関するセオリーをどのように組み合わせて使うか,その実践例である。以下,順に内容を概説する。
I.ポートフォリオ(2社株モデル)
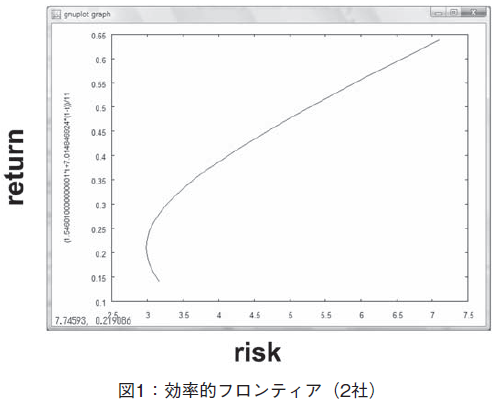
2社の株をブレンドし,その株価の収益率から,リスク(軸名risk)および期待収益率(軸名return)を求めて,図1に示すような,効率的フロンティア曲線を描く。株価データは,資料[2]を参照した。株価データからの収益率の求め方は,資料[3]の方法に従った。
2社の株をブレンドする比率は,媒介変数t を使って,t :(1−t)とした。MAXIMA では下記のように記す。この例では,A 社とC 社の株の収益率がリストA, C に用意されている。N は収益率のデータ数である。
AC : makelis(t A[i]*t+C[i]*(1−t), i, 1, N);
期待収益率rtnAC および,リスクriskAC の定義はMAXIMA では,以下のように表現できる。不偏分散の(N−1)で割る定義もあるが,ここでは不偏分散ではなく分散を用いた。つまりN とした。
rtnAC: sum(AC[i], i, 1, N)/N;
riskAC: sqr(t sum((AC[i]−rtnAC)^2, i, 1, N)/N);
リスク最小点を求め,その時の媒介変数t の値を求め,図1において,そのリスク最小点よりも上側部分を,効率的フロンティアとして描画した。下記プログラムでは,リスク最小点のt 値をtval と名付け,0< t < tval の範囲で,リスク−期待収益率のカーブを描いた。ここでは,空売りは無いと仮定した。
【267頁】
plot2d([parametric, riskAC, rtnAC],[t, 0, tval]);
2社の期待収益率の大小が逆の場合は,tval < t <1の範囲でカーブを描く。
II.ポートフォリオ(3社株モデル)
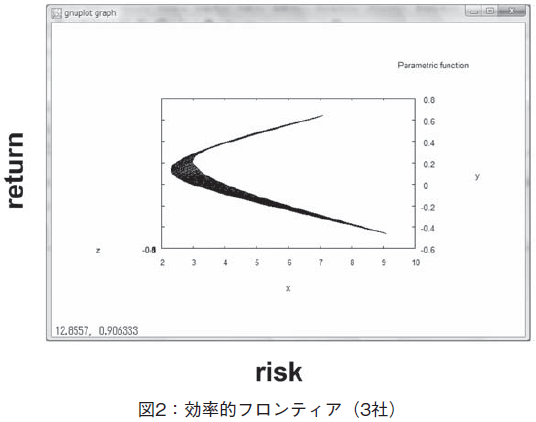
3社の株をブレンドし,その株価の収益率から,リスク(軸名risk)および期待収益率(軸名return)を求めて,図2に示すような,効率的フロンティア曲線を描く。同じ期待収益率に対して,最もリスクが小さい点を結んだカーブが効率的フロンティア曲線となる。図2のグラフ上には,それ以外の点も描画されている。
3社の株をブレンドする比率は,媒介変数t1, t2, t3を使って,MAXIMA で下記のように記す。
ABC: makelis(t(A[i]*t1+B[i]*t2+C[i]*t3), i, 1, N);
リスクと期待収益率は,2社モデルと同じように計算する。リスク最小点の計算は,ラグランジェの未定乗数法[4]を用いて,以下のように解いた。その際の制約式はt1+t2+t3=1である。
Lagr: varABC+lambda*(1−t1−t2−t3);
float(solve([dif(f Lagr, t1)=0, dif(f Lagr, t2)=0, dif(f Lagr, t3), t1+t2+t3=1],[t1, t2, t3, lambda]));
上記のように方程式を解くことで,まず,リスク最小点が求められる。
次にグラフィクスであるが,MAXIMA には,2つの媒介変数t, s を用いて,2変数の多変数関数を3次元グラフィクスとして描画する機能があるので,それを用いてグラフィクスを描いた。そのために,媒介変数を3個から2個,t とs に置き直して(以下の式ABC2参照),リスクriskABC2及び,期待収益率rtnABC2の式を定義し直している。3次元グラフィクスの垂直軸方向は,この場合,使わないので,0と設定している:[riskABC2, rtnABC2, 0]。
【268頁】
ABC2: makelist((A[i]* t+B[i]*s+C[i]*(1−t−s)), i, 1, N);
rtnABC2: sum(ABC2[i], i, 1, N)/N;
riskABC2: sqrt(sum((ABC2[i]−rtnABC2)^2, i, 1, N)/N);
plot3d([riskABC2, rtnABC2, 0],[ t, 0, 1],[s, 0, 1]);
媒介変数によるグラフィクス描画関数が用意されているので,簡単にグラフィクスが描画できる。
III.住宅ローン
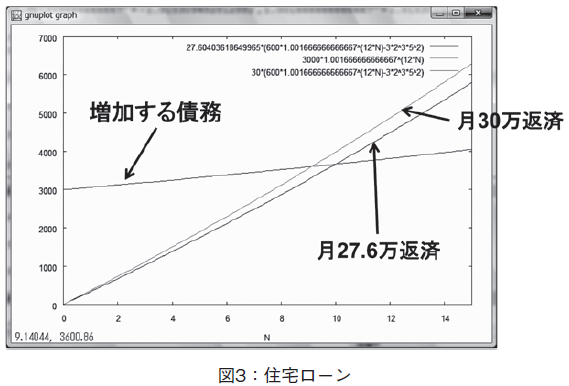
住宅ローンの問題をグラフィクスで描画した(図3参照)。債務が複利で増加するカーブ,および,毎月の返済を積み立て貯金とみなした場合のカーブ,そして,その2本のカーブが交わる点が,完済日であることをグラフィクスで表した。
ここで解いている問題では,与えられたデータは,年利2%で,3000万円のローンを10年完済で組んだ場合であり,未知数は,毎月の返済額である。住宅ローンの公式F3A とセオリー1を組み合わせて,月々の返済額を以下のように求める。答えは27.6万となる[4]。
F3A: PV = nusum(rvalue(/ 1+r/Times)(^ i*Times/rTimes), i, 1, N*rTimes);
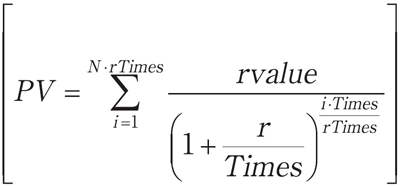
float(solve(ev(F3, PV:3000, r:0.02, rTimes:12, Times:12, N:10), rvalue));
関数nusum は,Σの計算を行う。上記で,方程式はF3の1式のみなので,角括弧で括っていない。
【269頁】
公式中の変数名であるが,返済額:rvalue,1年あたりの返済回数:rTimes(=12),1年あたりの複利計算回数:Times(=12),としている。
図3のグラフィクスでは,計算で求めた返済額を用いて,債務の増加関数と返済の積立貯金の増加関数が,完済日10年で交わるようすを示した。さらに,3本目の増加関数として,返済額を27.6万から30万に増額した場合,返済期間が早まるようすを描画した。
IV.年金
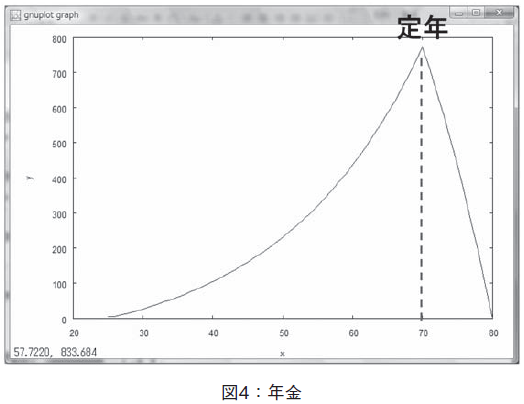
特定額の年金を定年後の一定期間受け取るために必要な貯金額を求める問題をグラフィクス化した。グラフィクスは,金利5% のもと,定年後にむけて25歳から70歳まで,毎年同額貯金していくようす(貯金の増加関数),及び,定年後,貯金を受け取っていくようす(貯金の減少関数)を示した(図4参照)。このグラフィクスは,人生の貯金額を非常にシンプルにモデル化したようすを示している。
年金に関する公式は以下のひとつのみとした。
F3B: PV=nusum(avalue(/ 1+r/Times)(^ i*Times/aTimes), i, 1, N*aTimes)
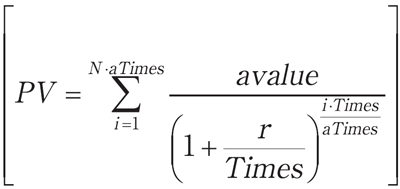
公式F3B は,定年時に必要な貯金額を算出する。変数avalue は毎回の年金受け取り額,aTimes は,1年間に年金を受け取る回数である。以下は,この公式を使った例である。
olve(ev(F3B, r:0.05, avalue:100, aTimes:1, Times:1, N:10), PV);
【270頁】
PV について解くことで,定年時に必要な貯金額PV を求める。
次に,その額を定年時に貯金できるために必要な,25歳から70歳までの定額貯金額を計算する。まず,定年時に必要な貯金額S[70]を,25歳の時点での現在価値に割り引く。これをPV2とラベル付けする。
PV2: ev(S[70](/ 1+r/Times)(^ N*Times), r:0.05, N(: 70−25), Times:1)
ここでは,公式F1A の将来価値(Future Value)と現在価値(Present Value)の公式を,PV について解いて使っている。そしてPV に,S[70]を代入している。
次に,住宅ローンのF3A の公式を用いて,以下のように,25歳から70歳までの定額貯金額を計算する。
F3A: PV=nusum(rvalue(/ 1+r/Times)(^ i*Times/rTimes), i, 1, N*rTimes);
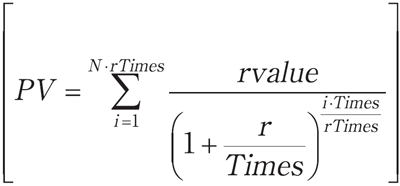
float(ev(solve(F3, rvalue), PV: PV2, r:0.05, N(: 70−25), rTimes:1, Times:1));
住宅ローンは積立貯金のようにローンを返済するが,年金の場合も考え方は,同じなので,この公式が適応できる。年金の場合,S[70]が達成額であるが,これをローンの債務額としてみなせば,毎回の貯金額が求められる。
公式F3A とF3B は全く同じ内容であるが,変数をavalue 及びrvalue と変えた方が考えやすいと考え,あえて統合しなかった。
V.債券:残存期間が長いほうが修正デュレーションが大
VI.債券:利回りが小さいほうが修正デュレーションが大
VII.債券:クーポンが大きいほうが修正デュレーションが小
上記3つは,いずれも債券価格に関する3次元グラフィクスであるので,同様のアプローチで解ける。公式集では,債券は確定利付債券を仮定している。
使う公式は,債券価格F2である。
F2: PV=
nusum(c*F/cTimes(/ 1+r/Times)(^ i*Times/cTimes), i, 1, N*cTimes)+F(/ 1+r/Times)(^ N*Times);
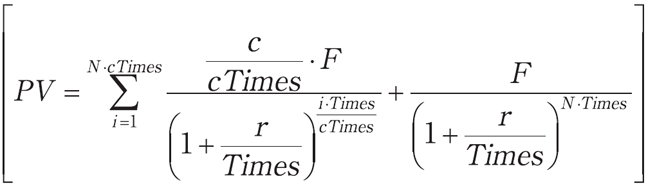
各変数は,以下の通り,r: 利回り,c: クーポン率,F:額面,N:残存期間(満期),cTimes:1年あたりのクーポン受取回数,Times:1年あたりの複利計算回数。例えば,[利回り,満期(残【271頁】存期間),価格]の3次元グラフィクスを描きたい場合,クーポン率と額面は,以下のように固定する必要がある。4次元以上のグラフィクスは描けないからである。
p1: ev(F2B, c:0.04, cTimes:1, Times:1, F:100);
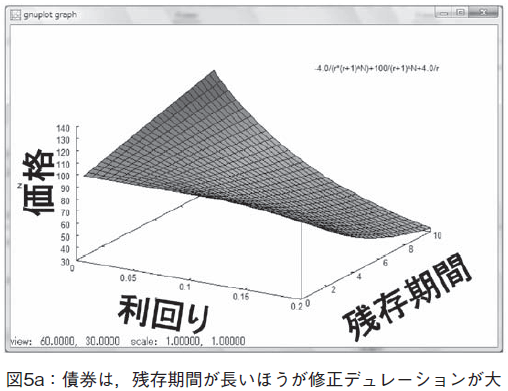
この式に,p1とラベルを付けて,p1式の右辺をrhs 関数で取りだし,以下のように3次元プロットすると,図5a にあるようなきれいな3次元曲面が描ける。範囲は利回りが20%まで,満期は10年までとした。
plot3d(rhs(p1),[r, 0, 0.2],[N, 0, 10]);
次に,残存期間を1年,5年,9年に固定して,この債券価格の3次元グラフィクスを切断した際のカーブを求める。
p2: ev(F2B, c:0.04, cTimes:1, Times:1, F:100, N:1);
p3: ev(F2B, c:0.04, cTimes:1, Times:1, F:100, N:5);
p4: ev(F2B, c:0.04, cTimes:1, Times:1, F:100, N:9);
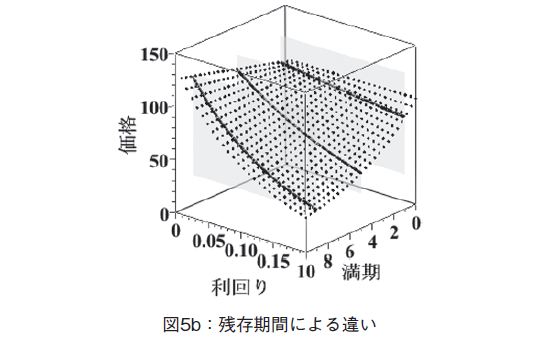
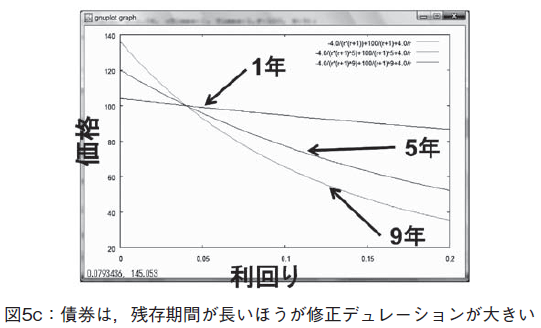
上記のように,異なる残存期間の値を代入して,公式F2を評価する。その式3個に対して,異なるラベルp2, p3, p4を付けた。これを一括してグラフィクス表示すると,図5b 図のようになる(これはMaple で描いた図である)。これを2次元平面に投影したようすは,以下のようになる(図5c 参照)。
債券価格の公式F2を使って,満期利回りを求めるためには,以下のように各変数に値を代入して,利回りr について,式を解けばよい。
float(solve(ev(F2, c:0.04, cTimes:1, PV:90,Times:1, N:3, F:100), r));
この場合,N =3で,式は3次式となるので,解は虚数解2個,実数解1個となる。この中から,【272頁】(i MAXIMA での表記は“%i”)を含む虚数解を除き,人手で実数解を求めなくてはならない。
r =0.078713293408408。
実数解だけを求める方法としては,readonly: TRUE; と設定した後,solve()の代わりに,algsys()を使う方法もMAXIMA では用意されている。
VIII.債券:価格と修正デュレーション
次に,債券の価格・利回り曲線と,修正デュレーションのカーブを同時に描画してみる。公式は,修正デュレーションF1C を用いる。
F1C: Dm=−1./PV*’dif(f PV, r);
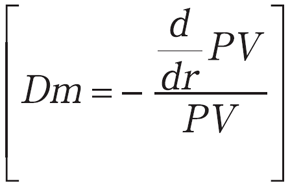
【273頁】
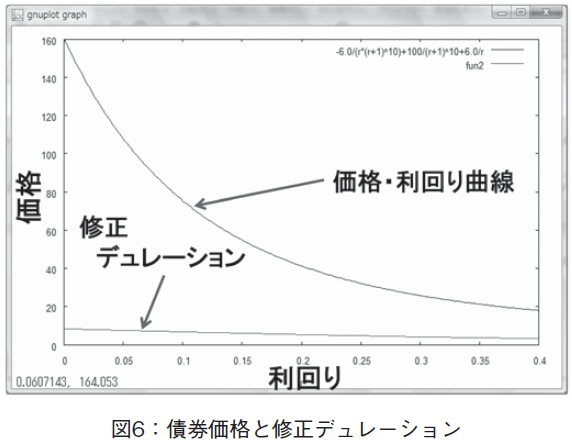
修正デュレーションの式に,債券価格F2の公式を代入し,Dm 及びPV について解く。
sol: solve([F2, F1C],[Dm, PV]);
その結果は,式2個のリストとなるので,以下のように1個目の式の右辺を取りだし,そこに与えられたデータを設定し,評価し,その後に,微分を実行する。
ev(rhs(so[l 1[]1]), N:10, c:0.06, cTimes:1, Times:1, F:100), diff;
この結果,以下のような修正デュレーションが求まるので,それを2次元表示した(図6参照)。
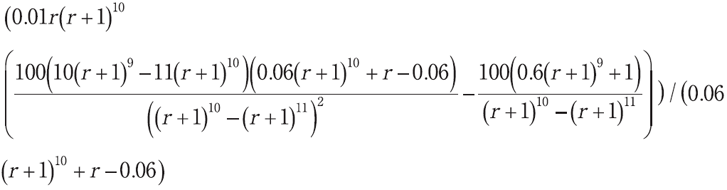
この例でも分かるように,金融工学の数学では,10次以上の式が頻繁に出てくるので,解を人手で求めることは不可能であり,数式処理ソフトウェアを使うことが必須となる。
IX.イミュニゼーションにおけるテイラー展開
ポートフォリオのイミュニゼーションとは,市場金利の変動によって,債券利回りが変動した場合でも,ポートフォリオの価値が債務(debt)の価値と一致するように,ポートフォリオを組むことである。金利(利回り)の変動に対する,現在価値の変動は,テイラー展開によって近似する。イミュニゼーションの場合は,ポートフォリオ側の価格変動のようすと,債務側の価格変動のようすを一致させるため,1次近似まで合わせる,あるいは2次近似まで合わせるようにポートフォリオを組んでいく。
【274頁】
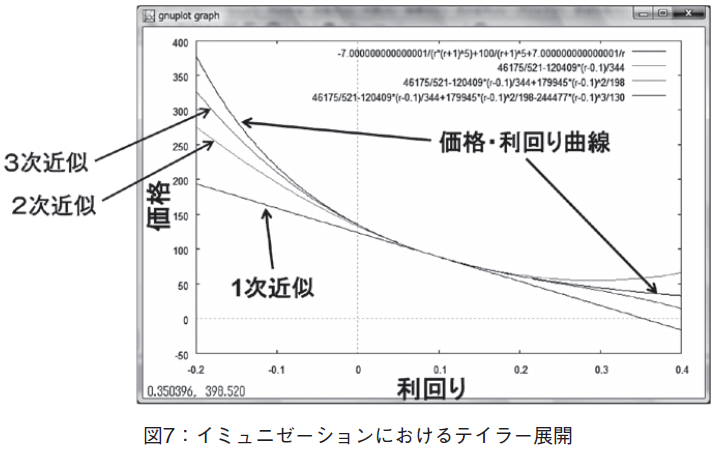
ここでは,ある債券の利回り変動に対する債券価格(現在価値)の変動のようすをテイラー展開で求め,その近似のようすをグラフィクス表示する。
以下のように,債券価格の公式F2に,条件データを設定し,その式をp1とラベル付けする。
p1:ev(F2, N:5, c:0.07, cTimes:1, Times:1, F:100);
その式の右辺のみを取りだして,テイラー展開する。MAXIMA では,テイラー展開関数が用意されているので,それを使う。以下では,r =0.1(10%)を中心として,1次近似,2次近似,3次近似を行っている。
t1: taylo(r PVexpr, r, 0.1, 1);
t2: taylo(r PVexpr, r, 0.1, 2);
t3: taylo(r PVexpr, r, 0.1, 3);
イミュニゼーションでは,1次近似あるいは2次近似までしか行わないが,数学的に見ると,次数をあげていくにつれて,近似がよくなるようすが理解できる(図7参照)。
イミュニゼーションは,このようにグラフィクス表示することで,中心とする利回りから,変動した場合,価値がどの程度,債務の現在価値と,かい離しているかがよく分かる。一定以上に金利が変動した場合に,再度,ポートフォリオを組み直さなくてはならないという,リバランスの必要な理由も,グラフィクスを使えば,説得力のある説明ができるであろう。
X.スポットレートによる債券価格の計算
スポットレートは,期間に依存して決まる利回りのシーケンスである。例えば,スポットレートが,1年単位で,s[: 1.0, 1.4, 1.6, 1.7, 1.8, 1.85, 1.87](単位%)で与えられたとする。(図8参照)この値から,割引係数d[0, k]が求められ,その割引係数から,期間k と期間(k+1)
【275頁】
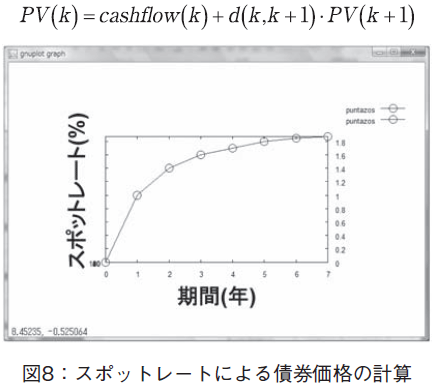
の間の割引係数d[k, k+1]が求められる。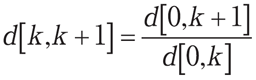
債券のキャッシュフローが与えられた場合,期間k におけるキャッシュフローの値cashflow[k]を用いて,債券価格を,逆向きに漸化式で求めていく方式がある[5;6]
PV[k]=cashflow[k]+d[k, k+1]× PV[k+1]
この計算方式では,最後のキャッシュフローの値を,最初に与える。ここでは,クーポン率4% の残存期間7年の確定利付債券を考えるとすると,以下のような初期条件となる。
PV[7]=104
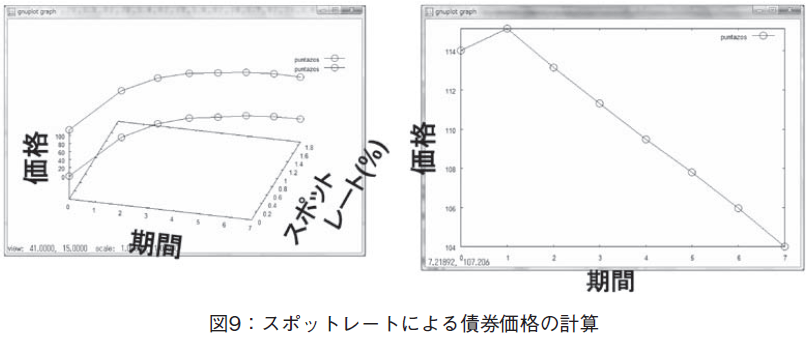
予め,期間の割引係数の値を計算しておき,それを使い,漸化式を時間に遡って計算していくと,PV[0]として,債券の現在価値,価格が求まる。
この計算方式は,漸化式を後ろから計算していくという考え方が多少わかりづらいので,グラフィクスを使って説明することを試みた。図9にあるように,縦軸にPV をとり,PV=0の平面にスポットレートのカーブを描く。その値を使って,N=7から,N=0まで,順を追って,【276頁】PV[k]の値を計算して,3次元空間にプロットする。スポットレートカーブの平面を合わせて描くことで,それを使って漸化式を計算することが印象づけられ,理解が容易となる。
4. 金融工学の数学教育のための学習支援システム
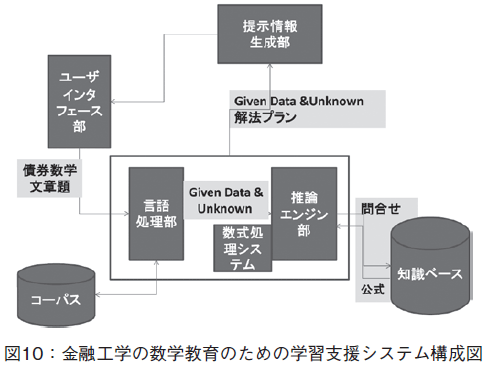
我々は,金融工学の数学教育のための学習支援システムの構築を提案し,現在,研究を進めている。対象は,「債券ポートフォリオの管理に関する数学文章題」である。研究の最終目標は,学生が入力した,システムにとって初見の日本語で書かれた金融工学数学文章題を解析し,解析プランを作成し,動的に教材を作成し,それを提示しながら,学生の推論および,問題解法を支援する,というものである。本システムの構想についての詳細は[7]を参照して頂きたい。図10にシステム構成図を示した。
図11に,学生が使うユーザインタフェースのイメージ図を示した。学生に提示する教材の中

【277頁】
には,このようにグラフィクス教材も必要であり,それを作成するためのテンプレートとなる教材を作り,データベース化しておく必要がある。Graphics10は,そのような目的で造られたデータベースである。
本学習支援システムの研究課題としては,以下のような項目がある。
・言語処理部:簡略化された文章を対象に,Given Data とUnknown を抽出
・言語処理部:文脈依存をGivenData だけから判別可能かどうか,研究する必要有り
・コーパス:ユニークなセマンティクスのラベル付け(シノニムの処理)
・知識ベース: 公式ミニマムセット及び,メタレベルでの公式表記(本当に必要な小さい公式集を作りたい)
・推論エンジン部: 適切な公式を検索し,最適かつ最短な解法プランを作成(システムが演繹推論を行う)
・推論エンジン部:オンデマンドな数式変換 (具体的には数式処理のsolve で実装)
・推論エンジン部:セマンティクスレベルのラベルによる検索
本稿の付録とした「債券数学公式集MAXIMA 版」は,上記,「知識ベース:公式ミニマムセット」に相当するものである。この課題については,初期バージョンは完成し,現在はこれで十分であるか,評価に入っている。また,本稿の第2節で述べた,数式処理プログラムに関するセオリーは,上記の「推論エンジン部:オンデマンドな数式変換」の実装の方針となるものである。今後とも,システムの実現を目指して研究していきたい。
5. まとめ
本稿では,金融工学数学のためのグラフィクス教材のデータベースGraphics10のWEB サイトについて報告した。我々は「見て分かる数学」教育を実践している。金融工学数学は難しいと言われるが,グラフィクス教材を利用することで,理解できる学生の数を増やすことは可能である。また,高校数学の分野においても,学生に興味をもたせるような応用分野と教材を探している教師は多いと考える。そのような目的に合わせ,我々は,高校を含む,数学の授業において,グラフィクス教材をもっと多く活用してもらうためにこのサイトを開いた。学生の自宅からの利用も可能となった。
利用者数増大のため,数式処理ソフトウェアとしては,国内外で普及しているフリーソフトであるMAXIMA(マキシマ)を使った。本稿の目的は,MAXIMA のプログラムに関して,ユーザー(教員)自身が,パラメータを自由に変更でき,ユーザー独自の金融工学数学グラフィクス教材を作成できるようにすることである。学習院大学では,Maple がどのPC からでも利用できるようになっている。当該講義ではMaple で作成したプログラムを利用しているが,サイト公開にあたって,教材として利用しているプログラムをMAXIMA に翻訳して使った。MAXIMA とMaple では,関数などは若干が異なるが,問題なく翻訳できた。製品化されているMaple のほうが,安定して稼働する,グラフィクス機能が充実している,などのメリットがあるが,フリーソフトウェアでも充実したグラフィクス教材を作成できることが今回,確認できた。
教材の内容としては,グラフィクスが効果的に生かせるテーマをとして,ポートフォリオの【278頁】効率的フロンティア及びイミュニゼーションの描画,住宅ローン,年金の増加関数と減少関数の描画,債券価格の3次元的描画などを選んだ。
今後とも,見て分かる数学を実践し,また,世の中に普及させていきたいので,多種のグラフィクス教材を作成していく所存である。
本研究の一部は,平成22年度科研費基礎研究(C)一般「推論エンジン法による知識ベースの構築」(課題番号:22500231,代表者:白田由香利)による。ここに記して謝意を表します。


【279頁】



【280頁】
[1] 石野雄一,道具としてのファイナンス,日本実業出版社,2005。
[2] 株価チャートCD-ROM2010年秋,東洋経済新報社,2010。
[3] 大川勉,金融工学入門,阿吽社,2002。
[4] 白田由香利,悩める学生のための経済・経営数学入門3つの解法テクニックで数学アレルギーを克服!,共立出版,2009。
[5] D. G. Luenberger, Investment Science, Oxford University Press, 1998。
[6] デービッド・G・ルーエンバーガー,(邦訳)今野浩,鈴木賢一,枇々木規雄,金融工学入門,日本経済新聞社,2002。
[7] 白田由香利,橋本隆子,久保山哲二,金融工学の数学のための知識データベース構築の提案。情報処理学会研究報告,データベースシステム(DBS),Vol. 2010-DBS-150 No.5 2010。