�y355�Łz
����҃Z�O�����g�Ǝ������ɕω�����A�C�f�A���E�|�C���g�����u�����h�I�����f���ɂ��W���C���g�E�X�y�[�X����
���c�@�P�O
�T�@�͂��߂�
����҂͂��܂��܂ȗ��R�ōw������u�����h�����肵�Ă���B�����̏���҂́C�D���ȃ��[�J�[��������u�����h�Ƃ����悤�ɍD�݂≿�l�őI������u�����h�����߂Ă��邾�낤�B����C���i�������Ƃ������R�Ńu�����h��I���������҂������B���Ƃ��C�r�[���ЂƂ�I�Ԃɂ��Ă��C��□�̍D�݂őI�ԏ���҂�����C���i�𒆐S�ɏ��i�I�т��������҂�����B�܂�C����҂̃u�����h�I���ɂَ͈��������݂���B�����āC�ЂƂ�̏���҂��u�����h��I�����闝�R����Ɉ��Ƃ͌���Ȃ��B���Ƃ��C���i�̖��͂Ŕ��A�����Ă�������҂��C���܂��ܒl���������Ă����̂ŁC�i���������r�[�����w�����C�����ƁC���܂łƍl�������ς���Ă��܂��C���i�őI�������肷��̂ł͂Ȃ��C�i���ŏ��i��I�Ԃ悤�ɂȂ��Ă��܂���������Ȃ��B�܂�C�ߋ��̏��i�I�������̑I���ɉe����^�����̂ł���B
���c�i2009�j�́C���̂悤�ɑ��l�ȏ���҂̃u�����h�I�������f���������V�������f�����Ă��C���ۂ̃f�[�^�Ń��f�����������B���̌��ʂ͈ꉞ�����̂������̂ł��������C�s�\���ȕ������c�����B���c�i2009�j�̃��f���́C��ʓI�ȃu�����h�I�����f���ɃW���C���g�E�X�y�[�X�i���ꂼ��̎���������҂̃u�����h�I���̊�ł��鑽�����i���j��ł̃u�����h�̈ʒu�C������v���_�N�g��}�b�v�Ə���҂����ꂼ��̎����ŗ��z�Ƃ���ʒu�ł���C�A�C�f�A����|�C���g�i���z�_�j�j���������̂ł���B���̌����̃I���W�i���e�B�[�́C�A�C�f�A���E�|�C���g���ߋ��̕����̍w���Ɉˑ����āC�ƌv���Ƀ_�C�i�~�b�N�ɕω�����_�ł���B�����ł́C�ߋ��̍w���̗��z�_�ɑ���e���͂ǂ̎����ɑ��Ă������ł���ƍl�����B���̉���̓��f�����Ȃ�ׂ��ȒP�Ȃ��̂ɂ��āC���͂̊ȑf����}��Ƃ����Ӗ��ł͗L�p�Ȃ��̂ł��邪�C�K�����������I�Ƃ͌����Ȃ��B�Ⴆ�C�r�[���̃��[�J�[�ɑ���M���x�Ɗ������Ƃ����ӂ��̎��ł́C�������͉ߋ��̂�葽���̍w���ɉe������C�i���̕����ŋ߂̍w���̉e�����傫���\��������B�{�����̖ړI�̂ЂƂ́C�������ɉe�����قȂ�\�������郂�f�����\�z���C�f�[�^���͂��s���ă��f���������邱�Ƃł���B
�܂��C���c�i2009�j�̃��f���ł́C�ϑ��\�ȉߋ��̍w����p���āC�ƌv�Ԃَ̈������ߋ��̍w���Ɉˑ����ĕω����闝�z�_�Ƃ����`�Ń��f���������B�܂�C����҂̃u�����h�I���́C�ߋ��̏��i�I���Ƃ����C����҂��u����Ă���̈Ⴂ�Ɉˑ�����ƍl�����̂ł���B�������C����҂َ̈����́C���z�_�̈Ⴂ�ȊO�ɂ����݂���B���Ƃ��C����҂̉��i�ɑ��锽�y356�Łz���̒��x�͐l���ꂼ��ł��낤�B���̌����̂����ЂƂ̖ړI�́C��������������ҊԂ̊ϑ��\�ȕϐ��ɂ��Ȃ��َ��������f�������C�f�[�^�Ō����邱�Ƃł���B
���̘_���̂��ꂩ��̍\���͎��̂悤�Ȃ��̂ł���B�܂��C���ۂ̍w���f�[�^�������҂̃u�����h�I�����L�q���悤�Ƃ��郂�f���̓W�J�����r���[����B�����āC�{�����Œ�Ă���郂�f�����Љ�C���f�����X�L�����p�l���E�f�[�^�ɓK�p�������ʂ����B�Ō�ɁC����̉ۑ�ɂ��ċc�_����B
�Q�@�X�L�����p�l���E�f�[�^��p�����u�����h�I���̕���
�s�ꂪ��Ƃ̃}�[�P�e�B���O�ϐ��ɔ@���ɔ������邩�����ۂ̃f�[�^����m�F���悤�Ƃ���s�ꔽ�����͂Ɋւ��錤���́C���̏d�v������C���R�Ȃ���}�[�P�e�B���O�E�T�C�G���X�̕���Ŏ�v�Ȓn�ʂ��߂Ă����B���ɁC1980�N��ȍ~����\�ɂȂ����X�L�����p�l���E�f�[�^�́C�s��S�̂ł͂Ȃ��C���ꂼ��̉ƌv���@���ɐ��i���w�����Ă��������L�^�����ڍׂŁC�c��ȃf�[�^�����悤�ɂȂ����B�����ŁC�e�ƌv�̃u�����h�I�����C���i�₻�̑��̃}�[�P�e�B���O�ϐ���v���Ƃ��ĕ��͂��邱�Ƃ��C�s�ꔽ�����͂̎嗬���߂邱�ƂɂȂ�B
�����̏��i�J�e�S���[�ł́C�e�ƌv�����̍w���Ŕ������i�̐��͈�Ƃ������Ƃ����ʂȂ̂ŁC�ƌv���̕��͂ł́C������ł͂Ȃ��C�u�����h��I������m���͂��邱�Ƃ��K�v�ɂȂ�B�����ŁC�e�ƌv�̃u�����h�I���m���́C���̉ƌv���u�����h�ɑ��Ċ����Ă�����p�i���p�̓}�[�P�e�B���O�ϐ��Ɉˑ�����j�ɔ�Ⴗ��Ƃ����m�����f���ł��郍�W�b�g�E���f�����C���̃X�L�����p�l���E�f�[�^�ɓK�p����悤�ɂȂ����i�Ⴆ�CGuadagni and Little1983�j�B
�������C���ە��͂��s���Ă݂�ƁC�ƌv��������u�����h�̌��p���}�[�P�e�B���O�ϐ������ł͂��܂��������邱�Ƃ��o���Ȃ��B�����ŁC���f���̐����͂����コ���邽�߂ɁC�u�����h�E�_�~�[�i�e�ƌv�ɋ��ʂȃ}�[�P�e�B���O�ϐ��ł͑������Ȃ��u�����h�̉��l��\���u�����h�ɌŗL�Ȓ萔���j��p����悤�ɂȂ����B����ɉ����āC�O�Y�u�����h�w���_�~�[�i�O��w���_�~�[�j�Ȃǂ̃u�����h�E���C�����e�B�[�ϐ����p������悤�ɂȂ����B�u�����h����C�����e�B�[�ϐ��͉ƌv�Ԃł̃u�����h���l�̍��Ɖƌv�̍D�݂̎��ԓI�ȕω����������B�O��w���_�~�[�̏ꍇ�́C�O��w�������u�����h����艿�l�𑝂����Ɓi���C�����e�B�[�j�ɂ���āC�ƌv���ł̍D�݂̕ω��Ɖƌv�Ԃ̃u�����h���l�َ̈����𑨂���B
�u�����h����C�����e�B�[�ϐ��̑�\�i��Guadagni and Little�i1983�j�̒�Ă������̂ł���B�ނ�́C�u�����h���w���������Ƃɂ���āC���̃u�����h�ɑ��鈤���������C���C�����e�B�[���`������邪�C���̂��Ƃ͑O��w���̏ꍇ�݂̂Ɍ��������Ƃł͂Ȃ��C����ȑO�̍w�����u�����h�ɑ���]���ɍD�e����^����Ɖ��肵�C�u�����h�E���C�����e�B�[�ϐ������̂悤�ɒ�`�����B
�u�����h�E���C�����e�B�[hjt���ρE�u�����h����C�����e�B�[hjt�|�P+�i�P�|�ρj�Edhjt�|�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���i�P�|�ρj�E��m��m�|�P�Edhjt-m
�������Ch���ƌv�Cj���u�����hށCt�����Cdhjt-�P���O��u�����hj �w���_�~�[�C�O���ρ��P
�܂�C�u�����h����C�����e�B�[�͉ߋ����ׂĂ̍w���̉��d�a�ł���C�d�݂͑O��w������ԍ����i�P�|�ρj�ŁC���k��ɂ�Y�p�̂��߁C�ς������Ă����̂ł���B���������āC�y357�Łz�ς͋L���p�����^�[�ł���CGuadagni and Little �̃u�����h����C�����e�B�[�ϐ��́C�O��w���_�~�[����ʓI�ȃu�����h����C�����e�B�[���ʂ𑪒肷�邱�Ƃ��ł���B���̃u�����h�E���C�����e�B�[�ϐ��́C�ƌv���ЂƂ̃u�����h��������C���̃u�����h�ɑ��郍�C�����e�B�[�̒l�����C�����e�B�[�̏���ł���P�ɂȂ�C���̃u�����h�ɑ��郍�C�����e�B�[�͉����̂O�ƂȂ�B��ʓI�ɂ́C���C�����e�B�[�ϐ��͓��R����Ɖ����̊Ԃ̐��l����邱�ƂɂȂ邪�C����͍ŋ߂̍w���ɂ�荂���d�݂������ƌv���̃u�����h��V�F�A�ł���B�ς��傫���ƁC�u�����h�E���C�����e�B�[�ϐ��̓u�����h�E�V�F�A�ɋ߂��Ȃ�C�t�Ƀς��������ƁC�O��w���_�~�[�̒l�ɋ߂Â��Ă����B
�m���ɁC�u�����h�E�_�~�[�ƃu�����h�E���C�����e�B�[�ϐ���p����ƃ��f���̃t�B�b�g�͂��Ȃ�ǂ��Ȃ邪�C�u�����h�E�_�~�[�ɂ���ĕ\�����u�����h�̉��l��u�����h�E���C�����e�B�[�̓��e�𗝉����邱�Ƃ�����C�}�[�P�e�B���O�헪�ɑ��鎦���ɂ͖R�����B
�����ŁC���f���̐����͂����コ���邽�߂ɁC�u�����h�E�_�~�[�ɑウ�āC�W���C���g�E�X�y�[�X�i�������ł̃u�����h�̕z�u�C������v���_�N�g��}�b�v�Ə���҂̃A�C�f�A���E�x�N�g�����邢�̓A�C�f�A����|�C���g�j�����i�Е� 1990�C���@1996�CErdem�@1996�Ȃǁj�C�����ď���҂̍w���Ɉˑ����ăA�C�f�A����x�N�g�����邢�̓A�C�f�A����|�C���g��ω������邱�Ƃɂ���āC�u�����h�̉��l�ƃ��C�����e�B�[�̕ω��𗝉����悤�Ƃ��鎎�݂��s����悤�ɂȂ����i�����@2004�C���c�@�i1998�C2005�C2009�j�Ȃǁj�B
�����̃��f�����瓾��ꂽ�v���_�N�g�E�}�b�v��̃u�����h�̕z�u�����邱�Ƃɂ���āC�}�b�v�̂��ꂼ��̎����������Ӗ����Ă��邩�𐄑����邱�Ƃ��o���C����҂��u�����h�ɑ��Ċ����Ă��鉿�l�̊�𗝉����邱�Ƃ��o����B�܂��C�A�C�f�A���E�x�N�g������͂��ꂼ��̎��̏d�v�x���C�����ăA�C�f�A����|�C���g����͂��ꂼ��̎��ł̗��z�̐�����ǂ݂Ƃ邱�Ƃ��o����B�v���_�N�g�E�}�b�v�́C��ʂɂ́C�A���P�[�g��������̃f�[�^�����q���͂�I�D��A�Ȃǂɂ���ĕ��͂��C����邱�Ƃ��������C�X�L�����p�l���E�f�[�^�ɃW���C���g�E�X�y�[�X�ƃ}�[�P�e�B���O�ϐ���g�ݍ����f����K�p���ē�����v���_�N�g�E�}�b�v�́C���ۂ̍w���f�[�^���瓾��ꂽ���̂ł��邱�Ƃƃ}�[�P�e�B���O�ϐ��̉e���������������ꂢ�ȃ}�b�v���o���邱�Ƃ������ł���B
�R�@�W���C���g�E�X�y�[�X�ƃ}�[�P�e�B���O�ϐ���g�ݍ��u�����h�I�����f��
�����ł́C�W���C���g�E�X�y�[�X�ƃ}�[�P�e�B���O�ϐ���g�ݍ��u�����h�I�����f���̏����̑�\�I�Ȃ��̂Ƃ��āC�܂��Е��i1990�j�̃��f�����Љ�悤�B����́C���W�b�g�E���f���ɃA�C�f�A���E�x�N�g����p�����W���C���g�E�X�y�[�X��g�ݍ��u�����h�I�����f���ł���C���̃��f���ł́C�ƌv���e�u�����h�ɑ��Ċ�����m���I���p�́C�u�����h�̕z�u�ƃA�C�f�A���E�x�N�g���C�}�[�P�e�B���O�ϐ��C�����Č덷���Ɉˑ�����Ɖ��肷��B�u�����h�I���m���͊m��I���p���m���I���p- �덷���ɔ�Ⴕ�C�ȉ��̂悤�Ƀ��W�b�g�E���f���ɂ���Ē莮�������B
�I���m��hjt��exp {�m��I���phjt}�^��exp{�m��I���phit}
�������Ch���ƌv�Cj���u�����hށCt����
�m���I���phjt���m��I���phjt�{�덷��hjt
�y358�Łz
�����i�A�C�f�A���E�x�N�g��hm��z�ujm�j�{����hk��}�[�P�e�B���O�ϐ�hjkt+�덷��hjt
�������Cm �����C��ʂɂ͎��̑����͂Q�Ck �� k �Ԗڂ̃}�[�P�e�B���O�ϐ��C��hk���ƌvh�ɂƂ��Ẵ}�[�P�e�B���O�ϐ�k �̏d�v�x�B
�܂�C��ʂɌ����Ă���A�C�f�A���E�x�N�g���Ƃ̓}�b�v��ł̎��̏d�v�x�i�������C���̕����������Ƃ�����j�̂��Ƃł���C���̃��f���ł́C�i���̕����Łj�d�v�����Ă��鎲��ŕz�u���傫���u�����h�قNJm��I���p���傫���Ȃ�C�I�������m�����傫���Ȃ�Ƃ������Ƃł���B���̃��f������C��ł��q�ׂ��悤�ɁC�}�[�P�e�B���O�ϐ��̌��ʂ����������u�����h���l�̍\���𗝉����邱�Ƃ��o����v���_�N�g�E�}�b�v�������C�u�����h���l���`����Ƃ��̏d�v�x�C�}�[�P�e�B���O�ϐ��ւ̔����Ƃ����̉ƌv�Ԃłَ̈����𗝉����邱�Ƃ��o����B�������C���̃��f���̌��_�́C���f�������G�Ȃ��ƂŁC���ɖ��Ȃ̂́C�ƌv�Ԃَ̈�����\�����邽�߂Ƀ��f���̃p�����^�[�ł���A�C�f�A���E�x�N�g���C�u�����h�̕z�u�C�}�[�P�e�B���O�ϐ��̏d�v�x�̂����ŁC�A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x���X�̉ƌv�ɓ��L�̂��̂ɂȂ��Ă��邱�Ƃł���B�܂�C�f�[�^��100�ƌv������C100�g�̃A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x�𐄒肵�Ȃ���Ȃ�Ȃ����ƂɂȂ�B����͌����I�ł͂Ȃ��̂ŁC���ʂ̃A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x�������������̃}�[�P�b�g�E�Z�O�����g�̑��݂����肵�C����̊ȑf�����}���Ă���B
�܂��C���̃��f������͏ւ̈ˑ����i�ߋ��ɍw�������u�����h�̉e���j�ɂ��Ēm�邱�Ƃ͏o���Ȃ��BErdem�i1996�j�́C�W���C���g��X�y�[�X��őO��w���u�����h�ƈʒu���߂��u�����h�قǍw�������m���������Ȃ�Ƃ��������ƁC���̋t�ňʒu���߂��قǍw�������m�����Ⴍ�Ȃ�o���G�e�B�[�E�V�[�L���O�����f���������B�������C���̃��f���ł͑O��w���u�����h�̉e���͈̔͂��}�[�P�e�B���O�ϐ��̏d�v�x�ɂ͂���Ȃ��B�Ⴆ�C�O��w�������u�����h�ɂ���ĉ��i��L���̏d�v�����ς�邱�Ƃ͂Ȃ��B�܂��C�W���C���g��X�y�[�X�ւ̉e���������ƃo���G�e�B�[��V�[�L���O�Ƃ������ۂɌ����Ă���B
���c�i1998�j�́C�O��w���u�����h�̉e�������̏d�v�x�ł���A�C�f�A����x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x�ɉe����^���C�ω�������Ƃ������f�����Ă����B�܂�C���̃��f���ł́C�u�����h�̕z�u�͏̔@���ɂ�����炸���ł��邪�C���̏d�݂ƃ}�[�P�e�B���O�ϐ��̏d�v�x���O��w�������u�����h�Ɉˑ����ĕω�����̂ł���B�i���̍����u�����h�́C�ɂ�����炸�i���������u�����h�ƔF�m����邪�C�i�����d�����邩�ǂ����͌��ݎg���Ă���u�����h�����ł��邩�ɂ���ĕω�����B
�����ɁC���̃��f���ł́C����҂َ̈��������̏���҂����ʂ��Ă���ɂ���Ă��Ȃ�̕����������ł���ƍl���āC�i�O��w���u�����h�̉e���j�ɂ���ď���҂َ̈�����������C�����ɐ���̊ȑf����}���Ă���B�܂�C����҂͑O��w�����C���ݎg�p���̃u�����h�ɂ���ăZ�O�����g������C���̃Z�O�����g���Ɉ�g�̃A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x�����L����ƍl����B���̂��Ƃɂ���āC�Z�O�����g�̐��̓u�����h�̐��ƂȂ�C�Z�O�����g�̃T�C�Y�͓��Y�u�����h�O��w���Ґ��ƂȂ�̂ŁC�Z�O�����g���ƃZ�O�����g�E�T�C�Y�̐���Ƃ������Ȗ���������邱�Ƃ��ł��C�ȕ����m�ۂ��邱�Ƃ��ł���B���_�́C�����Ă���Ɋ�Â����ƌv�َ̈������C�O��ǂ̃u�����h���w���������Ƃ������Ƃ݂̂ɂ���ĕ\�����Ă��邱�Ƃł���B
�����i2004�j�́C�e�ƌv�̃A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x���w�������y359�Łz�ЂƂ̃Z�O�����g���瑼�̃Z�O�����g�̂��̂Ɋm���I�ɕω�����Ƃ����Е����f���̊g�����f�����Ă��C�x�C�Y���v�w�̎�@�ł���MCMC �@��p���ăp�����^�[�𐄒肵���B���̃��f���ɂ���āC�Е��̃��f���ł͏o���Ȃ������C�ƌv�������Ă���A�C�f�A���E�x�N�g���ƃ}�[�P�e�B���O�ϐ��̏d�v�x�̕ω��𑨂��邱�Ƃ��o����悤�ɂȂ����B�������f���͉ƌv�̃Z�O�����g�Ԃł̈ړ��Ɋւ��āC���c�i1998�j�̃��f������ʓI�ŕ��G�Ȍ��ۂ𑨂��邱�Ƃ��o����B�������C���̃��f���ł́C�ւ̈ˑ����������I�ɑg�ݍ��܂�Ă��Ȃ��̂ŁC���̕ω����N�������͕�����Ȃ��B�܂��C����̕��G�����������ꂽ�Ƃ͌����Ȃ��B
�܂��C�������w�E���Ă���悤�ɁC�A�C�f�A���E�x�N�g����p�������f���ɋ��ʂ̎�_�Ƃ��āC����œ���̒l���D�܂��Ƃ������ۂ�\���ł��Ȃ��Ƃ������Ƃ�����B�A�C�f�A���E�x�N�g���E���f���ł̓u�����h�̕z�u���傫����Α傫���قǁC�u�����h�͏���҂ɍD�܂�邩��ł���B�R�[�q�[�̓K�x�ȋ�݂Ƃ����悤�Ȓ��ԓI�Ȓl���D�܂��悤�ȏꍇ�́C�A�C�f�A���E�|�C���g�E���f����p���Ȃ���Ȃ�Ȃ��B�t�ɁC�傫�Ȓl���D�����ꍇ�ł��C�A�C�f�A���E�|�C���g�̒l���傫���Ȃ�C�傫���l�قǍD�����Ƃ������Ƃ�\�����邱�Ƃ́i�ߎ��I�Ɂj�\�ł���B
���c�i2005�j�́C�A�C�f�A���E�x�N�g���E���f����葽���̌��ۂ��L�q���邱�Ƃ��\�ŏɈˑ������A�C�f�A���E�|�C���g�E���f�����\�z�����B���̃��f���ł́C�O��w�������u�����h�Ɉˑ����ăA�C�f�A���E�|�C���g�ƃ}�[�P�e�B���O�ϐ��̏d�v�x���ω�����B�O��w�������u�����h�ɂ��e���Ƃ����l�����́C���c�i1998�j�̃A�C�f�A����x�N�g������f���Ƌ��ʂł���B�����ł��C����҂͑O��w�����C���ݎg�p���̃u�����h�ɂ���ăZ�O�����g������C���̃Z�O�����g���Ɉ�g�̃A�C�f�A���E�|�C���g�ƃ}�[�P�e�B���O�ϐ��̏d�v�x�����L���Ă���B���̂��Ƃɂ���āC�Z�O�����g���̓u�����h���ƂȂ�C�Z�O�����g�̃T�C�Y�͓��Y�u�����h�w���Ґ��ƂȂ�B���̃Z�O�����e�[�V�����Ɋւ���A�v���[�`�̌��_�����c�i1998�j�Ɠ��l�ŁC�����Ă���Ɋ�Â����ƌv�َ̈������C�O��ǂ̃u�����h���w���������݂̂ɂ���ĕ\�����Ă��邱�Ƃł���B
���c�i2009�j�̃��f���́C����҂̏ւ̈ˑ���O��w���݂̂Ɍ��肹���C�ߋ��̑����̍w���ւ̈ˑ��Ɋg�債���C�v���_�N�g�E�}�b�v�ƃA�C�f�A����|�C���g�����u�����h�I�����f���ł���B���̃��f���ł̃A�C�f�A����|�C���g�ɂ��Ă̍l�����͈ȉ��̂悤�Ȃ��̂ł���B����ƌv���ЂƂ̃u�����h�݂̂��w�����Ă���̂ł���C���̃u�����h�̈ʒu�ƃA�C�f�A����|�C���g�͈�v���Ă���ƍl���ėǂ��B�����ӂ��̃u�����h�����w�����Ă���̂ŁC�u�����h��V�F�A������ł���C�A�C�f�A���E�|�C���g�͂ӂ��̃u�����h�̈ʒu�̕��ςł��钆�ԂɈʒu���Ă���ƍl����̂����ʂł��낤�B���̕\�P�́C�ӂ��̉ƌvA�CB �ǂ�������C�ӂ��̃u�����h���w�����Ă���Ɖ��肵���w���@��̉ˋ�̃u�����h�I����\�ɂ������̂ł���B

�y360�Łz
�ǂ���̉ƌv���ӂ��̃u�����h�����w�����C�u�����h��V�F�A�͊e�u�����h50���œ���ł��邪�C�ƌvA �͂ӂ��̃u�����h��p�ɂɃX�C�b�`���O���Ȃ���w�����C�ƌvB �͍ŋ߂R��u�����h�Q���w�����Ă���B���̏ꍇ�C�ƌvA �̃A�C�f�A����|�C���g�͂ӂ��̃u�����h�̒��Ԃɂ���C�ƌvB �̃A�C�f�A����|�C���g�̕��́C�ŋ߃u�����h�Q�𑱂��čw�����Ă���̂ŁC�u�����h�Q�̈ʒu�ɂ����Ƌ߂Â��Ă���\���������ƍl����̂����R�ł��낤�B�܂�C�ƌv���u�����h��V�F�A�������l�i�����ł́C50���j�ł��C�w�������ɂ���āC�A�C�f�A����|�C���g�̈ʒu�͈قȂ�ƍl����̂���莩�R�ł���C���ꂪ�_�C�i�~�b�N�ɕω�����A�C�f�A����|�C���g�Ƃ����l�����ł���B�����O��w�������u�����h�ɂ���Ă̂݃A�C�f�A����|�C���g�����܂�Ɖ��肷��ƁC�ƌvA �̃A�C�f�A���E�|�C���g�̈ʒu�����肷�邱�Ƃ͍���ł��낤�B�܂��C�ƌvB �́C�w���@��R����w���@��S�̊Ԃɑ傫���A�C�f�A����|�C���g���ω��������ƂɂȂ�B
��ɏЉ��Guadagni and Little�i1983�j�̃u�����h�E���C�����e�B�[�ϐ��́C�ŋ߂̍w���ɂ�荂���d�݂������ƌv���̃u�����h��V�F�A�Ȃ̂ŁC�����p����C�w���o���ɔ�Ⴕ�ĕω�����A�C�f�A���E�|�C���g�Ƃ����l���������f�������邱�Ƃ��ł���B�܂�C�ƌv�̃A�C�f�A����|�C���g��Guadagni and Little�i1983�j�̃u�����h�E���C�����e�B�[�ϐ��ɂ���ďd�ݕt����ꂽ�u�����h�̕z�u�̉��d���ςƍl����悢�B�\�P�̃P�[�X�ł́C�ƌvA �̍w���́C�L���p�����^�[�ł���ς�傫������C�ߋ��̑����̍w���ɏd�݂����邱�ƂɂȂ�̂ŁC�u�����h�E���C�����e�B�[�ϐ��̒l�̓u�����h�E�V�F�A�ɋ߂Â��C�u�����h�E�X�C�b�`���[�ł��邱�Ƃ����܂��\���ł���悤�ɂȂ�B�܂�C�u�����h�E�X�C�b�`���[�̗��z�_�́C���O�ɔ������u�����h�̈ʒu�֑傫���߂Â����Ƃ͂Ȃ��C�ߋ����������낢��ȃu�����h���������e�����C�����̃u�����h�̕z�u�̒��ԓI�Ȉʒu���Ƃ�B���������āC�ǂ̃u�����h���������D���Ƃ������Ƃ��Ȃ��B�t�ɁC�ƌvB �̍w���́C�ς��������Ȃ�ƍŋ߂̍w���ɂ�葽���d�݂����̂ŁC�ƌv�̗��z�_�͈��̃u�����h�̕����֑傫�������C���C�����e�B�[�����܂��\�����邱�Ƃ��ł���B��ʓI�ɂ��C�ƌv���u�����h�E���C�����ł���C�����u�����h��������̂ŁC�ŋ߂̍w��������C���̉ƌv�����C�����ł���u�����h��m�邱�Ƃ��ł���B
�ƌv�̃A�C�f�A����|�C���g���u�����h�E���C�����e�B�[�ϐ��ɂ���ďd�ݕt����ꂽ�u�����h�̕z�u�̉��d���ςƂ��邱�Ƃ̃����b�g�́C�w���@��ɕω����C�ߋ��̑����̍w���Ɉˑ�����ƌv�̃A�C�f�A����|�C���g�̃��f�������\�ɂ��邾���ł͂Ȃ��B�u�����h�E���C�����e�B�[�ϐ���p���邱�Ƃɂ���āC�u�����h�̕z�u��������ł���C�ƌv�̃A�C�f�A����|�C���g�͂�������v�Z���邱�Ƃ��o����B���������āC�ƌv���������瑝���悤�ƁC���f���̃p�����^�[��S�����₳���ɁC�ƌv���ɈقȂ�A�C�f�A���E�|�C���g�𐄒肷�邱�Ƃ��o���C����ɂ���ĉƌv�َ̈����������邱�Ƃ��o����B
��q�̂悤�ɁC���̃��f���́C�ߋ��̍w���̃A�C�f�A���E�|�C���g�ɑ���e���͂ǂ̎����ɑ��Ă������ł���Ɖ��肵�����C����͕K�����������I�Ƃ͌����Ȃ��B�܂�C�ƌv�͎������Ƀu�����h�E�X�C�b�`���[�i�ߋ��̑����̍w���ɉe�������j�ł�������C�u�����h�E���C�����ł������肷��\�������邩��ł���B�܂��C����҂َ̈����́C�ߋ��̍w���Ɉˑ��������z�_�̈Ⴂ�ȊO�ɂ����݂���B�\�P�̗�̂悤�ɁC�ς̒l���������Ƃ����ł͂Ȃ��C�ƌv���ɈقȂ�\�������邵�C�}�[�P�e�B���O�ϐ��ɑ��锽�����قȂ邩������Ȃ�����ł���B����̌����̖ړI�́C���̂ӂ��̉���ɔ����Ȃ����f�����Ă��C���ۂ̃f�[�^���y361�Łz�����邱�Ƃł���B
�S�@����҃Z�O�����g�Ǝ����ɕω����闝�z�_�����u�����h�I�����f��
�����ł́C�{�����ł̒�ă��f������{�I�ȃA�C�f�A����|�C���g����f������\�z���Ă������B��{�I�ȃA�C�f�A����|�C���g����f���ł́C�ƌv���e�u�����h�ɑ��Ċ�����m���I���p�́C�u�����h�̕z�u�ƃA�C�f�A���E�|�C���g�i���z�_�j�C�}�[�P�e�B���O�ϐ������Č덷���Ɉˑ�����Ɖ��肷��B�I���m���́C�m��I���p���m���I���p�|�덷���ɔ�Ⴗ�郍�W�b�g�E���f���ɂ���Ē莮�������B
�I���m��hjt��exp {�m��I���phjt}�^��exp {�m��I���phjt}
�������Ch���ƌv�Cj���u�����h�Ct����
�m���I���phjt���m��I���phjt�{�덷��hjt
�����|�i�z�ujm�|�A�C�f�A���E�|�C���ghmt�j�Q�{����k��}�[�P�e�B���O�ϐ�hjkt�{�덷��hjt
�������C�A�C�f�A���E�|�C���ghmt�͑�t ���̉ƌvh �ɂƂ��Ă�m ����ł̃A�C�f�A����|�C���g��\���Ă���B
�A�C�f�A���E�|�C���g�E���f���ł́C�u�����h�̕z�u�Ɨ��z�_�Ƃ̋��������Ȃ��ق������p���傫���ƍl����̂ŁC�m���I���p�̎��ł̃u�����h�̕z�u�Ɨ��z�_�Ƃ̋����ɂ͕��̕��������Ă���B���������āC�����A�C�f�A���E�|�C���g���傫����C�u�����h�̕z�u���傫���u�����h���傫�Ȍ��p�������ƂɂȂ�B�t�ɁC�����A�C�f�A���E�|�C���g����������C�u�����h�̕z�u���������u�����h���傫�Ȍ��p�������ƂɂȂ�B
��q�̂悤�ɁC���c�i2009�j���f���ł́C�ƌv�̃A�C�f�A����|�C���g��Guadagni and Little�i1983�j�̃u�����h�E���C�����e�B�[�ϐ��ɂ���ďd�ݕt����ꂽ�u�����h�̕z�u�̉��d���ςƍl����B���������āC�ƌv�̃A�C�f�A����|�C���g�͎��̂悤�ɏ������Ƃ��ł���B
�A�C�f�A���E�|�C���ghmt�����z�ujm��u�����h�E���C�����e�B�[hjt
�������C�u�����h�E���C�����e�B�[jhjtj��Guadagni and Little�i1983�j�̃u�����h�E���C�����e�B�[�ϐ��ł���B�܂�C
�u�����h�E���C�����e�B�[hjt���ρE�u�����h�E���C�����e�B�[hjt�|�P+�i�P�|�ρj�Edhjt�|�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���i�P�|�ρj�E����n�|�P�Edhjt-n
�������Cdhjt�|�P���O��u�����hj �w���_�~�[�C�O���ρ��P�B
����ɁC�{�����̒�ă��f���ł́C�A�C�f�A���E�|�C���g�ւ̃u�����h�E���C�����e�B�[�ϐ��̉e���͎������ɈقȂ�\�������̂ŁC�L���p�����^�[�i�ρj�͎������ɈقȂ�ƍl����B
�u�����h�E���C�����e�B�[hjmt����m�E�u�����h����C�����e�B�[hjmt�|�P�{�i�P�|��m�j�Edhjt�|�P
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ���i�P�|��m�j�E����mn�|�P�Edhjt-n
�y362�Łz
�A�C�f�A���E�|�C���ghmt�����z�ujm��u�����h�E���C�����e�B�[hjmt
�������C�O����m ���P�ł���B
����ɁC�{�����ł́C�ƌv�َ̈����͉ߋ��̍w���ɂ���ĕω�����A�C�f�A����|�C���g�����ɂ͂Ƃǂ܂�Ȃ��ƍl���C����ҊԂ̊ϑ��\�ȕϐ��i�ߋ��̍w���j�ɂ��Ȃ��َ�������݃N���X�E���f���ɂ���ă��f��������iAndrews et. al. 2002�j �B�����ŁC�s��ɂ́CS �̂��ꂼ��̋L���p�����^�[�i�ρj�ƃ}�[�P�e�B���O�ϐ��̏d�v�x�����i�x�l�t�B�b�g�E�j�Z�O�����g�����݂��C�ƌv�͂����̃Z�O�����g�̂����ꂩ�ɁC�f�[�^���Ԃ�ʂ��āC�m���I�ɏ�������Ɖ��肷��B�ς͎������ɈقȂ�̂ŁC�S����S �~��������������B�܂��C�ς��قȂ�̂ŁC�A�C�f�A���E�|�C���g���Z�O�����g���ƂɈقȂ�B�Z�O�����gs �ɏ�������ƌvh �̃u�����h�I���m���͎��̂悤�ł���B
�I���m��hsjt��exp {�m��I���phsjt}�^��exp { �m��I���phsit}
�������Ch���ƌv�Ci�C j���u�����h�Ct�����Cs���Z�O�����g�B
�m���I���phsjt
��-���i�z�ujm �|�A�C�f�A���E�|�C���ghsmt�j�Q+ ����sk��}�[�P�e�B���O�ϐ�hjkt+ �덷��hsjt
�������Cm�����Cm���Q�Ƃ���Ck��k �Ԗڂ̃}�[�P�e�B���O�ϐ��B
�A�C�f�A���E�|�C���ghsmt�����z�ujm��u�����h�E���C�����e�B�[hsjmt
�u�����h�E���C�����e�B�[hsjmt����sm�E�u�����h����C�����e�B�[hsjmt�|�P�{�i�P�|��sm�j�Edhjt�|�P
�����ł́C�u�����h�̕z�u�́C�̔@����Z�O�����g�ɂ�����炸���ł���Ɖ��肷��B�u�����h�̕z�u�͈��ƍl�����ق����C�v���_�N�g��}�b�v���}�l�W���A���ɉ��߂��₷������ł���B�ƌv�̓Z�O�����gs �Ɏ��̂悤�Ȋm���ŏ�������B
�Z�O�����g�����m��hst��exp{�Z�O�����gs �ɌŗL�̒萔}�^�� exp{�Z�O�����gq �ɌŗL�̒萔}
���ꂼ��̃Z�O�����g�ɌŗL�̒萔�͉ƌv�����̃Z�O�����g�ɑS�w����ʂ��ď�������\����\�����Ă���B
�T�@�����ؕ���
�f�[�^�́C�H���i�̃p�b�P�[�W����J�e�S���[�Ɋւ���X�L�����p�l���E�f�[�^1)�ŁC70�ƌv�̂T�u�����h�̍w���Ɋւ�����̂ŁC�S�w����742��ł���B�u�����h�̏ڍׂ́C�\�Q�̒ʂ�ł���B
�y363�Łz
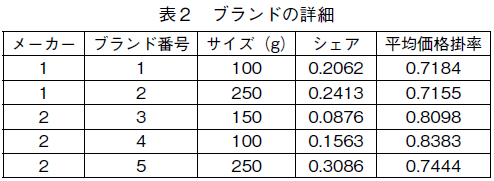
���̐��i�J�e�S���[�ɂ́C���ɂ������̃u�����h�����݂��邪�C���̂Q���[�J�[�̂T�u�����h�Ŏs��S�̂̔���̑������߂Ă���B�\�Q�̒��̃V�F�A�́C�����̂T�u�����h�̒��ł̃V�F�A�������Ă���B�\���ōł��V�F�A�������̂��ԍ��T�̃u�����h�i�ȉ��u�����h�T�ƌĂԁC���̑��̃u�����h�����l�j�ŁC�V�F�A�͖�30���ł���B���ɁC�V�F�A�������̂̓u�����h�Q�ł���C��24���̃V�F�A�������Ă���B�������C�u�����h�R�ƃu�����h�S�̈Ⴂ�̓T�C�Y�����ł���2)�C���̗��҂����킹��ƁC�������24���قǂ̃V�F�A�������Ă���B��ԃV�F�A���Ⴂ �u�����h�P�ł��C�V�F�A��20���ȏ゠��̂ŁC�V�F�A���猩��C���̂T�u�����h�͂��Ȃ�h�R�������������Ă���B
�u�����h�Q�ƃu�����h�T�́C�������@�ō���Ă��āC���[�J�[�ɂ���ĕ��y�u�����h�ƈʒu�Â����Ă���B����ɑ��āC�u�����h�P�C�R�C�S�́C�u�����h�Q�C�T�Ƃ͈Ⴄ����̐��@�ō���C�v���~�A���E�u�����h�Ƃ��Ĉʒu�Â����Ă���B���۔����̕W�����i�ɑ���䗦�ł��鉿�i�|��3)������ƁC���ςł̓u�����h�P�C�u�����h�Q�C�u�����h�T�̊|�����Ⴂ���C���ς����ł͓ǂݎ��Ȃ����ꂼ��̃u�����h�̉��i�헪�����݂��Ă���悤�ł���B
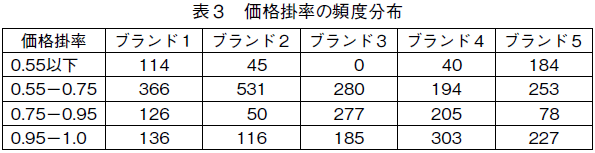
�\�R�́C�f�[�^���ԓ��̊e�u�����h�̉��i�|���̕p�x���z�����������̂ł���4)�B�u�����h�P�ƂT�͂قڒ艿�i�|����0.95�|1.0�j�Ŕ����Ă��邱�Ƃ��������C�������i�сC���ɕW�����i�̔��l�߂��i�|����0.55�ȉ��j�Ŕ����Ă��邱�Ƃ������B�t�ɁC�u�����h�Q�́C�u�����h�P��u�����h�T�قNjɒ[�Ɉ������i�тł͔����邱�Ƃ͏��Ȃ����C�������i�сi�|����0.55�|0.75�j�ň���I�ɔ����Ă��邱�Ƃ������B�u�����h�R�ƂS�͑��̃u�����h�ɔ�ׁC�W�����i�ߕӁi�|����0.75�|1.0�j�Ŕ����邱�Ƃ������C�l�����͂���قNjɒ[�ł͂Ȃ��C���i�͈��肵�Ă���悤�ł���B
�y364�Łz
��̃f�[�^�ɑ��Ăӂ��̃��f����K�p���čŖސ��肵�����ʂ��r�����B����ɂ́C�w�������Ȃ��S�ƌv�͏����C66�ƌv�̃f�[�^��p�����B���߂̃��f���́C���i�|�����}�[�P�e�B���O�ϐ��Ƃ��Ď������{�����ł̒�ă��f���ł���B�ӂ��ڂ̃��f���́C��ă��f���̗L�������m�F���邽�߂̃x�[�X���C���ł��鐙�c�i2009�j���f���ł���5)�B���̃��f�������l�ɉ��i�|�����}�[�P�e�B���O�ϐ��Ƃ��Ď��B���ꂼ��̃��f���ɂ��āC�Z�O�����g�����P����n�߂āC�����̃Z�O�����g�������f���𐄒肵�C���ʂ��r���čŗǂ̃Z�O�����g�������肷�邱�Ƃɂ����B����̍ہC�W���C���g�E�X�y�[�X�̎����͂Q�����Ƃ����B�܂��C��ă��f���ł́C�ߋ��̊e�w���̃A�C�f�A���E�|�C���g�ւ̉e���x�𑪂�L���p�����^�[�i�ρj�̓Z�O�����g�E�������ɈقȂ邪�C�ꕔ�̃Z�O�����g�ł͓������Ƃ���������ۂ������f�������肵���B����́C�������ɈقȂ�ς̐���l�����ʂ��Ă���ꍇ�Ƀ��f�������挒�Ȃ��̂ɂ��邽�߂ł���B���肳�ꂽ���f���̃f�[�^�ւ̓K���x��AIC�i�Ԓr�̏��ʊ�j��BIC�i�x�C�W�A�����ʊ�j�Ŕ�r�����̂��\�S�ł���6)�B
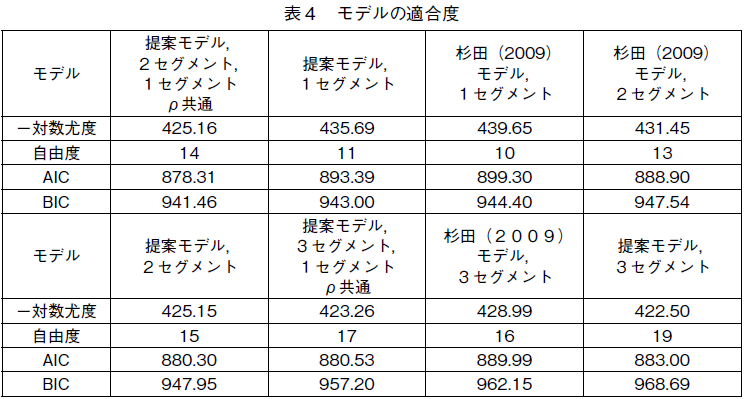
�\�S����CAIC �Ŕ�r���Ă�BIC �Ŕ�r���Ă��C��ă��f���̓K���x�����c�i2009�j���f���̓K���x�������Ă���̂�������BAIC �Ō���C�ł��ǂ��̂��C�ЂƂ̃Z�O�����g�ł̓ς��e�������ʂł���C�Q�Z�O�����g������ă��f���ŁC�Q�Ԗڂɗǂ��̂��C�Q�Z�O�����g�̒�ă��f���ł���BBIC �Ō���ƁC�����ł��ł��ǂ��̂��C��̃Z�O�����g�ł̓ς��Q�����Ƃ����ʂł���Q�Z�O�����g������ă��f���ŁC�Q�Ԗڂɗǂ��̂��C�P�Z�O�����g�̒��y365�Łz�ă��f���ł���B���������āC�ǂ���̎w�W�ł��ł��ǂ����ʂ��o�����ЂƂ̃Z�O�����g�Ńς��Q�����Ƃ����ʂł���C�Q�Z�O�����g������ă��f�����̗p����ׂ��ł���B�Z�O�����g�������Ȃ����f���̃p�t�H�[�}���X���ǂ��̂̓}�[�P�e�B���O�E�f�[�^�ɓK�p���ꂽ���݃N���X�E���f���ł͂悭�N���邱�Ƃł���B���̃f�[�^�ł��R�Z�O�����g�������f���̓K���x�͂Q�Z�O�����g�������f��������Ă��āC����ȏ�̃Z�O�����g�����l����K�v�͂Ȃ�����7)�B���̌�́C�̗p���ꂽ��ă��f���̐��茋�ʂ̉��߂ɂ��ċc�_��i�߂Ă����B�̗p�������f�����瓾��ꂽ�p�����^�[�̐���l�͕\�T�̒ʂ�ł���B
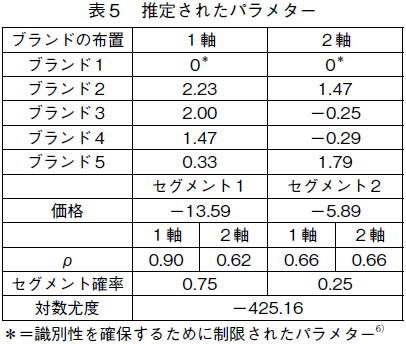
���̕\����C���̃��f�����瓾��ꂽ�ӂ��̃Z�O�����g�ł́C���i�ւ̔������傫���Ⴄ���Ƃ�������B��P�Z�O�����g�ɔ�ׁC��Q�Z�O�����g�̉��i�p�����^�[�̒l�͔����ȉ��ł���B�ς̒l�̓Z�O�����g�ԂňقȂ��Ă��邪�C���i�قǂ͑傫���قȂ��Ă͂��Ȃ��B���̂��Ƃ́C�����œ���ꂽ�ӂ��̃Z�O�����g�����i�ւ̔����̈Ⴂ�ɂ���ē����Â����Ă��邱�Ƃ������Ă���B���ꂼ��̃Z�O�����g�ւ̏����m���́C��P�Z�O�����g��75���ŁC��Q�Z�O�����g��25���ƍ�������C�����̉ƌv�����i�u���ł��邱�Ƃ�������B��P�Z�O�����g�̃ς͑�P����0.90�ŁC��Q����0.62�ł���B�܂�C��P���̓ς̒l�������̂ŁC�����̉ߋ��̍w���Ɉˑ����C�u�����h�E�X�C�b�`���O�������B����ɑ��āC��Q�Z�O�����g�ł́C�ς̒l�͂ӂ��̎��ŋ��ʂł���C0.66�ƒႢ�̂ŁC�ŋ߂̍w���̉e������r�I�傫���C���z�_�����̃u�����h�ɋ߂Â��Ă���B�u�����h�̕z�u�ɂ��ĉ��߂����₷�����邽�߁C�}�P�Ƀv���_�N�g��}�b�v��`�����B
�y366�Łz
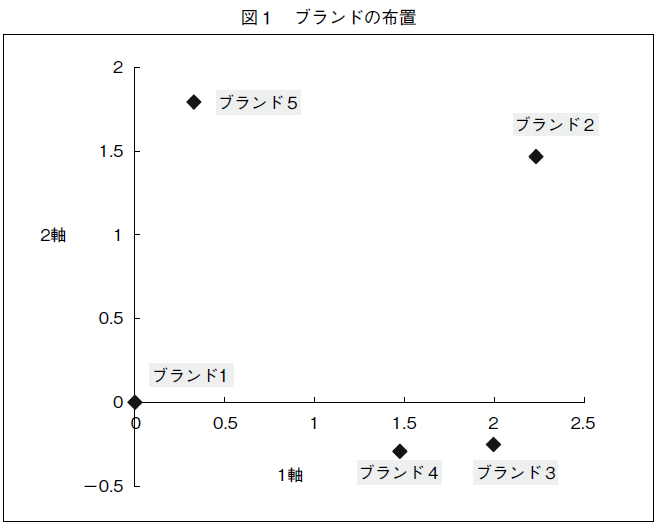
�}�P�̃}�b�v�ł́C�u�����h�̕z�u�́��ŕ\���Ă���8)�B�}�b�v�̉����Ƀv���~�A���E�u�����h�ł���u�����h�P�C�R�C�S���ʒu���C�}�b�v�̏㑤�ɂ������ȃu�����h�ł���u�����h�Q�ƂT���ʒu���Ă���B���������āC�Q���͐��@�̍��i�ɂ�閡�̍D�݁j��\���ƍl������9)�B����ɑ��āC�P���͉��i�C���[�W�̍�������킷�ƍl������B��q�̂悤�ɁC�u�����h�T�ƂP�͒艿�ƈ�����̍��i���i���j���������u�����h�C������n�C����[��v���C�V���O��p����u�����h�ŁC���ꂪ�}�b�v�̍����Ɉʒu���Ă���B���i���������肵�Ă���u�����h�Q�C�R�C�S�͋t�Ƀ}�b�v�̉E���ɂ���B����҂ɂ́C���i�헪�Ɋւ��čD�݂�����ƍl������B�ꕔ�̏���҂͉��i�����肵�Ă��邱�Ƃ��D�݁C���̏���҂̓`�F���[�E�s�b�L���O���ł���n�C�E���[�E�v���C�V���O���D�ނƍl�����邩��ł���B
�A�C�f�A����|�C���g����f���ł́C�A�C�f�A���E�|�C���g����߂��ʒu�ɂ���u�����h���D�����̂ŁC�A�C�f�A����|�C���g����f�������߂���ɂ́C�u�����h�̕z�u�ƃA�C�f�A���E�|�C���g�Ƃ̈ʒu�W�����ɂȂ�B���鎲��Ńu�����h�̕z�u���߂��u�����h���C����҂��瓯���悤�ɒm�o����C���̈Ӗ��𐄑����邱�Ƃ��o���Ă��C���ꂾ���ł͂ǂ̃u�����h�̕z�u��������D�ʂȂ��̂Ȃ̂��͕�����Ȃ��B�u�����h�̕z�u�����̒l������Ă����Ƃ��Ă��C���ꂾ���ł͕s���Ȉʒu�Ƃ͌����Ȃ��̂ł���B�}�Q�Ɛ}�R�́C���ꂼ���P�Ƒ�Q�Z�O�y367�Łz�����g�̃u�����h�̕z�u�Ɖƌv�̃A�C�f�A���E�|�C���g�̕��z�𗧑̓I�Ɏ������U�z�}�ł���B�e�ƌv�́C�Z�O�����g�ւ̏����m�����ő�i�Q�Z�O�����g�Ȃ̂ŁC�m����0.5�ȏ�j�̃Z�O�����g�ɏ�������Ɖ��肵�ĕ��z���v�Z����10)�B
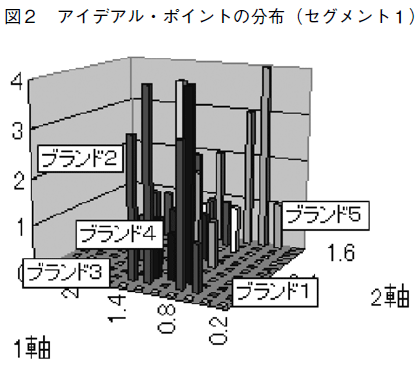
�Z�O�����g�P�ɂ�53�ƌv����������Ɛ��肳��C�����ł̓A�C�f�A���E�|�C���g���u�����h�T���邢�̓u�����h�R�C�S�̕t�߂ƃ}�b�v�̒����ɑ���������B�A�C�f�A���E�|�C���g���U�z�}�̒����ɑ����Ƃ������Ƃ́C�u�����h�̕z�u�̏d�S�i���ρj�߂��ɃA�C�f�A���E�|�C���g���ʒu���Ă���̂ŁC�u�����h�E�X�E�B�b�`���O�������N���Ă���Z�O�����g�ł���\�����������邪�C���i���x���������Ƃƍ��킹�čl����ƁC���̃Z�O�����g�̓X�B�b�`���[�������Z�O�����g�ł��邱�Ƃ������ł���B�܂��C��q�̂悤�ɁC��P���̓ς̒l�������̂ŁC�ŋ߂̍w������̃u�����h����C�����e�B�[�ϐ��ɑ���e���͏������B���������āC��P���ɂ��ẮC����҂̃A�C�f�A���E�|�C���g�͊ȒP�ɂ͈ړ����Ȃ��̂ŁC���i�헪�ɑ������҂̍D�݂͂��܂�ς��Ȃ��B�������C���̃Z�O�����g�ɂ͂��Ƃ��Ɖ��i���x����������҂������̂ŁC��P����̈ʒu�ɂ�����炸�C���̎������u�����h��������\���������B��Q���̃ς͔�r�I�l���Ⴂ�̂ŁC�ŋ߂̍w���̉e�����傫���B�܂�C���@�Ɋւ���D�݂͍ŋ߂̃u�����h�Ɉ��������₷���Ƃ������Ƃł���B����́C���̍D�݂͍��g���Ă���u�����h�ɂ��e������₷���Ƃ������Ƃł��낤�B
�y368�Łz
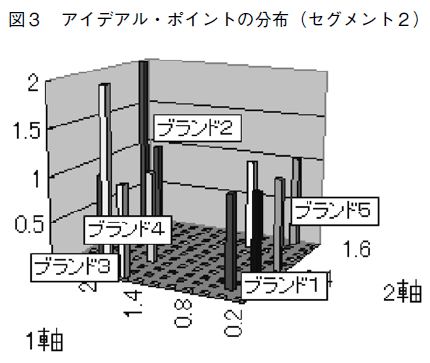
�Z�O�����g�Q�ɂ�13�ƌv����������B���̃Z�O�����g�ł́C�A�C�f�A���E�|�C���g�̕��z�͂��ꂼ��̃u�����h�̈ʒu�̂��ɕ��Ă���B���̃Z�O�����g�̃ς͑�P���C��Q���Ƃ�0.66�ł���̂ŁC�A�C�f�A���E�|�C���g�̈ʒu�͍ŋߍw�������u�����h�ɉe�������x��������r�I�傫���C�������C���Ƃ��Ɖ��i�����x���Ⴂ�Z�O�����g�Ȃ̂ŁC���g���Ă���u�����h����̃X�B�b�`���O�̉\���͒Ⴍ�C���C�����ȃZ�O�����g�ł���B�����[���̂́C�ǂ̃u�����h�ɂ��������炢�̐��̃t�@�������邱�ƂŁC����҂̐l�C���W�߂ėD�ʂɗ����Ă���u�����h�����Ɍ�������Ȃ����Ƃł���B��P�Z�O�����g���u�����h��X�C�b�`���[�������Z�O�����g�ł��邱�Ƃƍ��킹�čl����ƁC�}�[�P�b�g��V�F�A���h�R�����s��ł���̂����Ȃ�����B
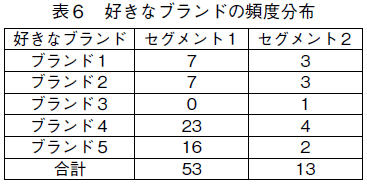
�\�U�́C�u�����h�̕z�u�Ɖƌv�̃A�C�f�A���E�|�C���g�Ƃ̋�������C���ꂼ��̉ƌv�̃A�C�f�A���E�|�C���g�ɍł��߂��u�����h���C���̉ƌv���D���ȃu�����h�Ƃ��āC�u�����h���ɂ��̃u�����h���D���ȉƌv�̕p�x��\�ɂ������̂ł���B���̕\������C�Z�O�����g�P�ł̓u�����h�S�����ău�����h�T�̐l�C���������Ƃ�������B�u�����h�R�ƃu�����h�S�͈ʒu�����ɋ߂��̂ŁC�u�����h�R���A�C�f�A���E�|�C���g����ł��߂��u�����h�ɂȂ�Ȃ������Ƃ������ƂŁC�l�C���Ȃ��Ƃ����킯�ł͂Ȃ��B�Z�O�����g�Q�ł́C��͂肻�ꂼ��̃u�����h���t�@�����m�ۂ��Ă���悤�ł���B����ł́C�T�u�����h�̉��i������ł��C���̂܂܃A�C�f�y369�Łz�A���E�|�C���g�̕��z�͏����I�ɂ����肵�āC�u�����h���h�R���Ă����Ԃ͑����̂ł��낤���B���邢�͂ǂꂩ�ЂƂ̃u�����h���D�ʂɗ��̂ł��낤���B���̋^��ɓ����邽�߂ɁC�u�����h�̉��i�͓���Ɖ��肵�āC�e�ƌv���T��w���𑱂����Ƃ���C�Ɖ��肵���w���V�~�����[�V�������s�����B�������ʂ�����邽�߁C�V�~�����[�V������100���Ȃ��C�ƌv�̃A�C�f�A���E�|�C���g�̓A�C�f�A���E�|�C���g�̕��ςƂ����B
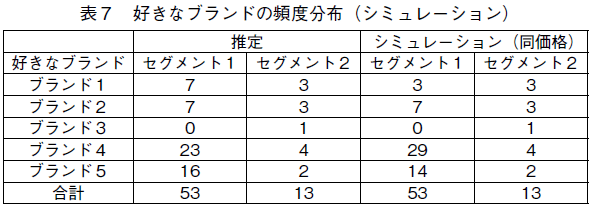
�\�V���u�����h�̕z�u�Ɖƌv�̃A�C�f�A���E�|�C���g�̋�������C�D���ȃu�����h��I�яo�������̂ł���B�\�U�Ɠ�������f�[�^�ł̌��ʂ��\�̍����ɂ���C�V�~�����[�V�����̌��ʂ����������̂��\�̉E���ɂ���B�Z�O�����g�P�ł́C�V�~�����[�V�����̌��ʁC�u�����h�S������ɐl�C��L���C�u�����h�P�̐l�C�����Ȃ茸��C�u�����h�T���l�C���������炵���B�u�����h�S���l�C��L�������R�́C�u�����h�S�̃}�b�v��ł̈ʒu�Ƃ��ꂼ��̎��ł̃ς̒l���W���Ă���悤�ł���B�u�����h�S�̕z�u�́C�P���Œ��ԓI�Ȓl�����C�Q���ł͂��Ȃ�Ⴂ�l�����u�����h�P�Ƃ͋߂��l�����B�P���̓ς��傫���C�A�C�f�A���E�|�C���g�͂��܂蓮�����C�A�C�f�A���E�|�C���g�����ԓI�Ȓl�ɑ����̂ŁC�ɒ[�Ȓl��蒆�ԓI�Ȓl���D�܂�C�Q���ł̓ς��������C�A�C�f�A���E�|�C���g�̓������傫���C�ɒ[�ȕz�u�ł��A�C�f�A���E�|�C���g���߂��Ɉړ����Ă���B���ʂƂ��āC�u�����h�P�ƂS�͂Q���ł͗D�͂����肹���C�P���Ńu�����h�P���ɒ[�Ȓl�Ȃ̂ŁC�u�����h�S���D�ʂɗ����߁C�u�����h�S�ɐl�C������錋�ʂƂȂ�B���̌��ʂ́C���ۂɂ̓u�����h�S�̉��i�������Ă��C�u�����h�S���}�[�P�b�g�E�V�F�A�ŕs���Ɋׂ��Ă��Ȃ��������Ƃ��l����C�[���̂������̂ł���C���̃u�����h�ɂƂ��Ă͌x�����Ȃ���Ȃ�Ȃ����ʂł���B���ɁC�u�����h�P�͉��i�C���[�W���ł���P���Ŕ����ɉ��i�������肷����Ǝv���Ă���\��������̂ŁC���i�헪���čl����K�v�����邩������Ȃ��B�Z�O�����g�Q�ł́C�D���ȃu�����h���قƂ�Ǖς���Ă��Ȃ��B����́C���Ƃ��Ƃ��̃Z�O�����g�̉��i�����x���Ⴍ�C���i�ɂ͉e�����ɂ����t�@���̑����Z�O�����g�ł��邱�Ƃ������Ǝv����B
�U�@���ʂ̗v��ƍ���̉ۑ�
�{�����ł́C����҃Z�O�����g�Ɖƌv���Ƀ_�C�i�~�b�N�ɕω����C�������ɋL���p�����^�[���قȂ�C�A�C�f�A���E�|�C���g���������u�����h�I�����f�����Ă����B�A�C�f�A���E�|�C���g�̃_�C�i�~�b�N�X�́C�������ɈقȂ�Guadagni and Little�i1983�j�̃u�����h�E���C�����e�B�[�ϐ���p���邱�Ƃɂ���ă��f�������C����҃Z�O�����g�͐��݃N���X�E���f���ɂ���ă��f���������B���ؕ��͂̌��ʂ���C�{�����Œ�Ă��ꂽ���f���̓K���x�́C���l�ȃ��J�j�y370�Łz�Y���������C����҃Z�O�����g�Ǝ������ɈقȂ�L���p�����^�[�������Ȃ����c�i2009�j���f���̓K���x�����邱�Ƃ������ꂽ�B���ؕ��͂̌��ʂ͈ꉞ�����̂������̂ł���ƌ����悤�B
����̃��f���̎��ؕ��͂́C�ߋ��̍w���̉e���͎������ɈقȂ�\�������邱�Ƃ������Ă���B�������C���ؕ��͂̌��ʂ́C�Q�Z�O�����g�̂����P�Z�O�����g�ɂ��Ă͈قȂ�C�����ЂƂ̃Z�O�����g�ł͓���ł���Ƃ������̂ł������̂Œ��ӂ��K�v�ł���B�e�����قȂ����Z�O�����g�ł́C�����̉��߂���C���i���̂��̂Ɋւ���I�D�́C���i���g�����тɕ⋭�����̂ō��g���Ă��鏤�i�̉e�����₷���̂ɑ��C���i�헪�ɂ��Ă͉ƌv�ɍD�������͏��Ȃ��悤�ŁC�n�C�E���[�E�v���C�V���O�̃u�����h������I�ȉ��i�̃u�����h�������悤�ɍw������邱�Ƃ������ꂽ�B
�}�[�P�e�B���O�ϐ��ւ̔������Z�O�����g���ɈႤ���Ƃ������ꂽ�B���ɁC����̕��͂ł́C���i�����x���傫���قȂ�u�����h�E�X�C�b�`���[�ƃu�����h�̃t�@���E�Z�O�����g�����ʂ��ꂽ�B�������C�P�Z�O�����g���������Ȃ���ă��f�������Ȃ�ǂ��p�t�H�[�}���X���������Ƃ������Ƃ́C����҂َ̈����̂��Ȃ�̕������ƌv���Ƀ_�C�i�~�b�N�ɕω�����A�C�f�A���E�|�C���g�ɂ���ăJ�o�[����Ă��邱�Ƃ������Ă���Ǝv����B
����̉ۑ�͑����B�ߋ��̍w���̉e�����������ɈقȂ�Ƃ������Ƃ͑����̃f�[�^�ɋ��ʂȂ̂��B�܂��C�A�C�f�A���E�|�C���g�ɂ���ĉƌv�َ̈��������Ȃ�̕����J�o�[�����̂������̃f�[�^�ɋ��ʂȂ̂��B�����ăς̒l�Ɖ��i�����x�ɂ͂Ȃ�炩�̊W������̂��B�����ɑ��铚����ɂ͂�葽���̎��ؕ��͂��s�����Ƃ��K�v�ł���̂͌����܂ł��Ȃ����C��萸�k�ȃ��f�����\�z���āC�u�����h�Ԃ̋��������ǂ��\�����C���f���̗��_�I�ȕ��͂��s�����Ƃ��K�v�ł���B
�m�Q�l�����n
�P�DAndrews, R. L.., A. Ainslie and I. Currim�i2002�j,�gAn Empirical Comparison of Logit Choice Models with Discrete Versus Continuous Representation of Heterogeneity,�hJounal of Marketing Research, 39, 4, 479-487.
�Q�DErdem, T.�i1996�j,�gA Dynamic Analysis of Market Structure Based on Panel Data,�hMarketing Science,15, 4, 359-378.
�R�DGuadagni, P. M. and J. D. C. Little�i 1983�j,�gA Logit Model of Brand Choice Calibrated on Scanner Data,�hMarketing Science, 5, 2, 203-238.
�S�DRamsay, J. O.�i1978�j,�gConfidence Regions for Multidimensional Scaling Analysis,�hPsychometrika, 43,241-266.
�T�DTversky, A. and I. Simonson�i1993�j,�gContext-dependent Preferences,�h Management Science, 39, 10,1179-1189.
�U�D���N�_�i1996�j������s��\���C����ґI�D�\���C�}�[�P�e�B���O�E�~�b�N�X���ʂ��������U�I�����f����w���w�_���x�i���w�@��w���w������jVol.43�CNo.2�C135-160��.
�V�D�Е��G�M�i1990�j�C��}�b�s���O���s�ꔽ�����f���v�C�w�}�[�P�e�B���O�E�T�C�G���X�x�C36�C13-27��.
�W�D������i2004�j�C�u�}�b�s���O�𗘗p�����s�ꔽ���̓��I���́v�w�}�[�P�e�B���O�E�T�C�G���X�x�CVol.12�CNo.1�E2�C1-23��.
�X�D���c�P�O�i1998�j�C�u�������ʂƃW���C���g�E�X�y�[�X��g�ݍ��u�����h�I�����f���v�C�w����ҍs�������x�CVol.5�CNo.2�C13-26��.
10�D���c�P�O�i2005�j�C�u�A�C�f�A���E�|�C���g�E���f���ɂ��W���C���g�E�X�y�[�X���́v�C�w�o�Ϙ_�W�x�i�w�K�@��w�o�ϊw��j�CVol.42�CNo.1�C21-32��.
11�D���c�P�O�i2009�j�C�u�_�C�i�~�b�N�ɕω�����ƌv���̃A�C�f�A���E�|�C���g�����u�����h�I�����f���ɂ��W���C���g�E�X�y�[�X���́v�C�w�o�Ϙ_�W�x�i�w�K�@��w�o�ϊw��j�CVol.46�CNo.2�C187-202��.
12�D���䐰�v�i1994�j�C�w���ϗʃf�[�^��͖@�x�C���q���X.