【303頁】
経営数学問題解法のための演繹推論支援教材作成ツール
要旨
経営数学の問題を解くためには演繹推論力の鍛錬は重要である。それは,多段階に渡る演繹推論を必要とする経営数学の問題も多数存在するからである。特に,金融数学の問題は演繹過程が複雑で長くなる傾向がある。金融数学の基本は債券数学であり,債券数学では,確定利き債券や,ポートフォリオによるイミュニゼーションなどの問題を扱う。債券数学を含む経営数学の教材を作成する際,問題なことは,演繹推論過程を示す教材作成に手間がかかることである。我々はこの手間のコスト削減を図りたい。そのため,解法プラングラフ・ジェネレータを開発した。本論文では,経営数学問題を解くための演繹推論法について論じる。そして,そのための教授法として我々の提唱する「推論エンジン法」を説明し,演繹推論過程を図解するための教材「解法プラングラフ」を作成するツール「解法プラングラフ・ジェネレータ」を報告する。
キーワード:演繹推論,債券数学のコンセプトモデル,解法プラングラフ,推論エンジン法。
1.始めに
経営数学の問題を解く場合,演繹推論が重要である。一般的に決定・判断を行う際には推論が重要であり,推論は論理的思考法の基本と言える。経営数学を学ぶ理由のひとつは,この推論力を向上させ,論理的思考力を鍛えることであると考える。
経営数学問題を解くことは,経営数学の知識の取得という近視眼的なものだけでなく,一般的な推論力を鍛えるために役立つ。経営数学を学ぶ目的が分からないという学生の問いかけに対しては,「将来,微分を使う場面は無いとしても,微分の演習は推論力を養うために,効果がある」というように,説明している。
学生が鍛えるべき推論法には,(1)演繹,(2)帰納,(3)アブダクション(仮説的推論) 【304 頁】 の3つがある。これらの推論力を鍛えることで,日常生活を送っていく上で必要な判断や経営上の判断の質が改善されていく[1]。
演繹は,一般的・普遍的な前提(ルール,セオリー,公式など)から論理的推論によって個別的な結論を導き出すことである。前提が真であれば,結果は必ず真である。世の中で広く使われている三段論法は,演繹である。帰納は,演繹の逆で,いくつかの個別の事例から,論理的推論によって一般的・普遍的な結論を導き出す。演繹と異なり,結論は正しいとは限らない。数学的帰納法は,名称が帰納法となっていてまぎらわしいが,帰納ではなく,演繹である[2]。アブダクションは,個別の事象を最も適切に説明しうる仮説を発想する推論である[3]。アブダクションによって発想された仮説は正しいとは限らない。
経営数学の問題解法で,どのような推論を行っているか考えてみる。
殆どの経営数学問題は,証明問題ではなく,解を求めるタイプの問題である。解を求めるタイプの問題を解くことは,問題で与えられたデータ(Given Data)から未知数(Unknown)へ
【305頁】
到る演繹過程を求めることである。その演繹過程を求めるためには,演繹,帰納,アブダクションのすべてを複合的に駆使して思考が行われていると,我々は考える。その思考の過程においては,アブダクションによって,仮説を立てて一歩先を予測しながら,逆方向に演繹推論を適応して,問題を解いているのではないかと考える。
学生が何度も同じ問題を間違える場合,あるいは問題が解けない場合,その理由は,個々の演繹ステップを十分理解していないためと考えられる。この対策として,正解である演繹推論過程を明確に見せることが,効果があると我々は考え,講義で演繹推論過程を描くことを実践してきた。
金融数学の問題では,特に,演繹過程が複雑で長くなる傾向がある。金融数学の基本は債券数学であり,債券数学では,確定利き債券や,ポートフォリオによるイミュニゼーションなどの問題を扱う[4]。債券数学を含む経営数学の教材を作成する際,問題なことは,演繹推論過程を示す教材作成に手間がかかることである。我々はこの手間のコスト削減を図りたい。そのため,演繹推論過程を図解するための教材「解法プラングラフ」を作成するツール「解法プラングラフ・ジェネレータ」を開発した。
本論文では,経営数学問題を解くための演繹推論法について論じる。そして,そのための教授法として我々の提唱する「推論エンジン法」を説明し,演繹推論過程を図解するための教材「解法プラングラフ」を作成するツール「解法プラングラフ・ジェネレータ」を報告する。
2.推論エンジン法
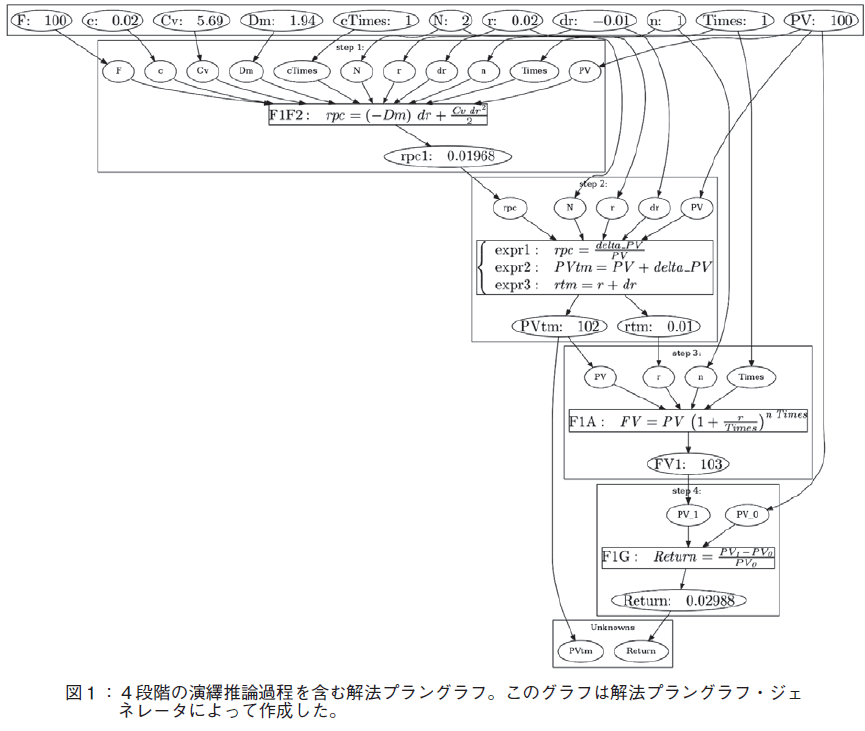
経営学科で数学を教えてきた経験から感じることは,多くの経営学科学生が経営数学を難しいと考えていることである。その理由として,(1)経済・経営に関する知識及び,数学に関する知識の不足,(2)知識からの演繹推論力の不足,があげられる。経済数学の場合,数学の知識と,経済・経営に関する知識が複雑に交じり合うため,演繹推論プロセスが複雑になるので,問題解法のための演繹推論が正しく行えないのである。図1に,問題解法のための演繹推論過程の例を示したが,ここでは4段階に渡る演繹推論を行っている。
以下,単に推論と言った場合は演繹推論のこととする。
さらに,学生の問題解決を困難にさせる理由としては,業界用語の不統一性問題が存在する。特に金融の分野で用語の不統一性の問題は大きい。これに関しては,我々は,債券数学に出てくる用語に対して,ユニークなセマンティクス・ラベル付けを行った。そして,ラベルの記述能力が適切であるか否かを検証するため,著名な教科書[4]の問題を記述した。その結果,このラベル集合を使って問題を記述する際,2つのラベルが衝突したり,ラベルの解釈があいまいになることもなく,記述できた[5]。債券数学については,このラベルは十分記述な能力があると言える。
経済数学教育のため,白田は,知識ベースに基づく「推論エンジンシミュレーション法」(以下,推論エンジン法と略す)という数学教授法を創案し,実際の講義においてこの教授法を実践してきた[6−8]。
推論エンジン法の特長は,学生に2種類の知識ベースを,頭の中に構築させる点である。推論エンジン法とは,コンピュータを全く使わない環境でも実践できる問題解決法である。以下は,コンピュータを使わない場合を想定して,学生に問題を解かせる場合である。
【306頁】
【307頁】

学生は,文章題で与えられたデータGiven Data を書き並べる。一方,問題で問われている未知数Unknown を書く。通常Given Data はトップに,Unknown はボトムに書き,Given DataからUnknown にいたるパスを,演繹推論によって発見していく。
経済の知識ベースには,経済の公式を,数学の知識ベースには数学公式が入っている。学生は,この公式を要素として取り出し,あるいは,Given Data のデータを要素として取り出し,推論プロセス(以下,「解法プラングラフ」と呼ぶ)を作っていく(図1参照)。図1はコンピュータによって作成した図であるが,このような図を学生が手でノートに書いていく。
解法プラングラフを書く際,時には,知識ベースにない式を自分で定義する必要もある。例えば,それはローカルなルールであったり,普遍的とは言えない関係式であったりする[3]。
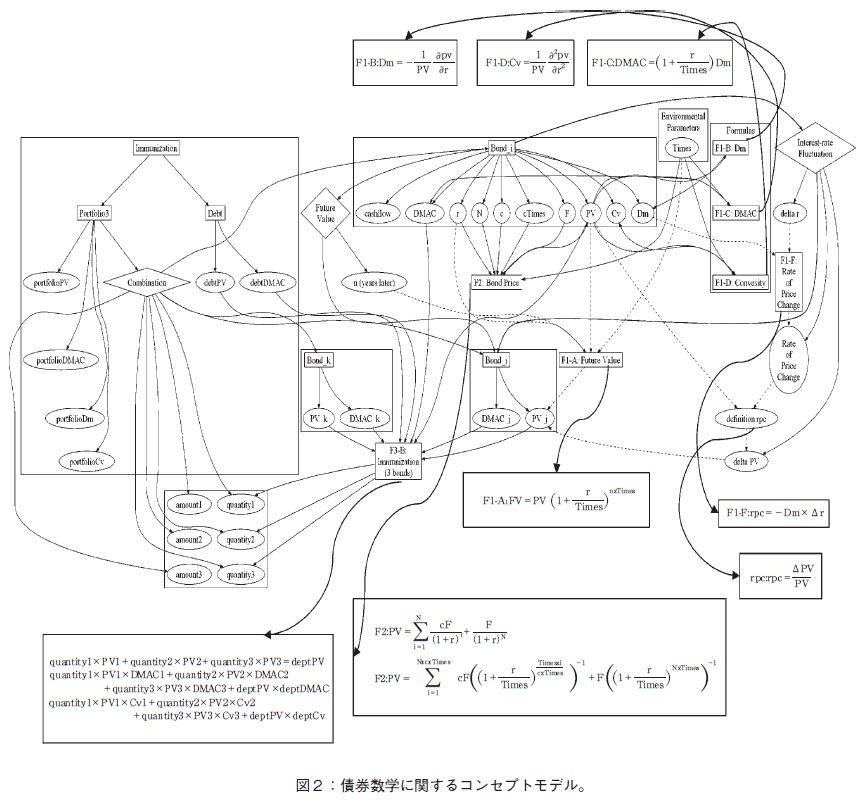
一般的に言って,使うべき公式を発見することは難しい。そこで,その支援のために,債券数学に関しては,図2のようなコンセプトモデルを作成した。このコンセプトモデルは,紙に印刷したものを学生に渡している。実際の教室では,図3のようにポスターを使って教えている。
コンセプトモデルとは,特定の分野(この場合は,債券数学である)に対して,そこで使う公式をEntity とみなして,公式間の関連を定義したEntity-Relationship ダイアグラム[9]である。関連Relationship として,金利変動(図中 Interest-rate Fluctuation),将来価値(Future Value),ポートフォリオ作成(Combination)の3つを定義した。本コンセプトモデルは,Given Data 及びUnknown から,その間の関連付けを行っている公式の発見を容易にする。
学生アンケートの結果からも,この推論エンジン法による学習効果が高いことが示された[6,8]。
我々は,推論エンジン法に基づき,学生を支援する学習支援システムを構築したい。学生は,解にいたるまでの,公式やセオリーを要素とする解法プラングラフを求めようと試みるが,それが困難な際に,システムが正しく演繹推論するための知識を提示し,学生が演繹推論の最適なパスを得るまで支援するようなシステムを最終ゴールとして作成したいと考える。
我々は現段階で,解法プラングラフを作成するツールを,既に開発した。このツールを,解 【307 頁】 法プラングラフ・ジェネレータと呼ぶ。次章以降では,解法プラングラフ・ジェネレータ及び,それによって生成した解法プラングラフについて述べる。
3.解法プラングラフ・ジェネレータ
解法プラングラフ・ジェネレータの入力データは,XML による解法プラングラフの記述であり,出力は,解法プラングラフである。特徴として,数式処理エンジンを使い,計算を行い,その値をグラフに埋め込んでいく点である。
例えば,確定利付き債券の価格の公式として以下がある。公式の番号付は我々が行ったものである。すべての変数はユニークなラベル付けがなされている。
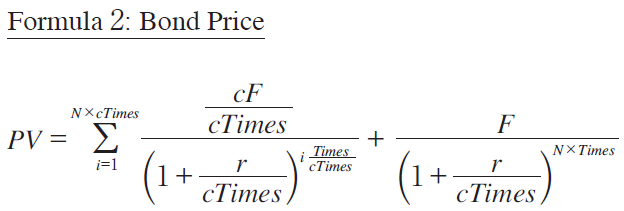
変数の意味は以下の通り:
r:満期利回り
F:額面
c:1年あたりのクーポン率
cTime:1年あたりのクーポン支払い回数
N:残存期間(年)
PV:現在価値
Times:1年あたりの複利計算回数
この公式を使う以下のような問題を解いてみよう。
────
例題: 半年ごとのクーポン支払いの債券で,額面100円,残存期間3年,クーポン率4%,満期利回り0.8%の債券の価格を求めよ。
────
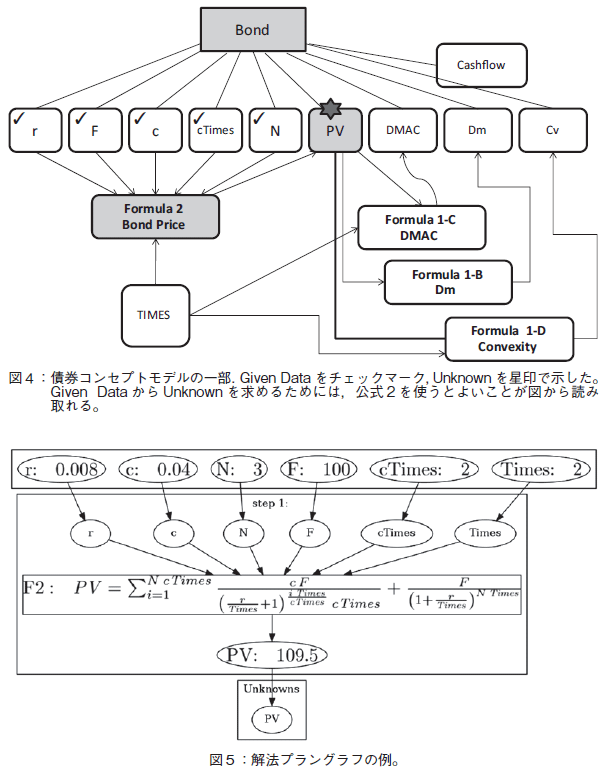
この問題を解くために必要な公式を探す際,コンセプトモデルを使う。コンセプトモデル上で,Given Data にチェックマークを,Unknown に星印でマークする。すると,Given Data からUnknown を求めるためには,公式2を使うとよいことが,容易に読み取れる(図4参照)
この公式を使って問題を解いた解法プラングラフを図5に示す。未知数の債券価格は109.5円である。
この解法プラングラフを描くためのXML スクリプトの本体を図6に示す。
図6のXML スクリプトからも分かるように,本XML スクリプトを専用エディタ無しで書
【308頁】
くことは,簡単ではない。XML のタグを間違えやすいからである。また,現状では,始めに解法プラングラフの最終形をイメージしてからでないとXML スクリプトは書けない。現在,我々が開発しようとしているのは,このXML スクリプトを対話的に作成するエディタである。
【310頁】

画面上に公式を並べていき,パスを作ることが可能か否か,試行錯誤することができるエディタを作成したいと考えている。
4.まとめ
経営数学の問題を解くためには演繹推論が使われる。しかし,演繹推論過程を示す教材を作成しようとすると手間がかかってしまう。我々はこの手間のコスト削減を図るため,解法プラングラフ・ジェネレータを開発した。解法プラングラフ・ジェネレータを使うことで,教師は複雑な推論プロセス(解法プラングラフと呼ぶ)も,容易に数値入りで描画することが可能となる。解法プラングラフを見ることで,学生は,どのように公式を組み合わせて演繹推論すべきかが分かる。
解法プラングラフを書くには,必要な公式を発見する必要がある。公式を覚えていても,公式間の関連をイメージすることは簡単ではない。そこで我々は,債券数学の公式間の関連を示したコンセプトモデルも作成した。このコンセプトモデルを用いることで,債券数学の問題を解く際,使うべき公式を発見しやすくなる。
今後であるが,本稿で報告した解法プラングラフ・ジェネレータをさらに使いやすいものにしていきたい。現バージョンではXML スクリプトを書かなくてはならないが,これは多くの 【311 頁】 ユーザによって煩雑な手間と思われる。また,XML スクリプトを書き始める前に,予め,解法プラングラフの最終形をイメージしてからでないとXML スクリプトは書けないことも問題である。現在,我々が開発しようとしているのは,このXML スクリプトを対話的に作成するエディタである。今後とも,推論エンジン法を学生が実践する際に,学生を支援するツールや教材を作成していきたい。
謝辞
本研究の一部は,平成23年度,科研費基礎研究(C)一般「推論エンジン法による知識ベースの構築」(課題番号:22500231,代表者:白田由香利)及び,平成23年度,学習院経済経営研究所GEM 研究プロジェクト「WEB 公開用経営数学のためのe-Learning システムの構築」により支援されました。ここに記して謝意を表します。
参考文献
1.瀧本哲史,武器としての決断思考。2011: 星海社。
2.山下正男,論理的に考えること。岩波ジュニア新書99。1985:岩波書店。
3.米盛裕二,アブダクション 仮説と発見の論理。2007:勁草書房。
4.Bodie, Z., A. Kane, and A.J. Marcus, Investments( 8th edition). 2008: McGraw Hill Higher Education; 8th Revised edition 版 (2008/9/30)
5.Shirota, Y., T. Hashimoto, and T. Kuboyama, A Concept Model for Solving Bond Mathematics Problems. Proc. of 21st European Japanese Conference on Information Modelling and Knowledge Bases, Estonia , June 2011: p. 6-10.
6.白田由香利,推論エンジンをベースとした経営数学教授法とそのアンケート評価。学習院大学経済論集,2010. 46(3): p. 31-41。
7.白田由香利,悩める学生のための経済・経営数学入門 3つの解法テクニックで数学アレルギーを克服! 。2009,東京:共立出版。
8.白田由香利,推論エンジンをベースとした経済数学教授法。情報処理学会研究報告,情報学基礎(FI),2009. Vol.2009-FI-95(No.10): p. 1-7。
9.飯沢篤志 and 白田由香利,データベースおもしろ講座。1993:共立出版。