【133頁】

Strategic commitment to pursue a goal other than profit in a Cournot duopoly

Dimitry Rtischev^＊

Abstract
Competition among profit-seeking firms in an oligopolistic industry inherently generates incentives for firms to commit to maximize a performance metric other than profit. We briefly review the underlying theory, analyze its ramifications in a Cournot duopoly, and consider feasibility constraints from the perspective of strategic management.

Keywords: oligopolistic competition, strategic commitment, strategic delegation

JEL classification: D43, L13, L21

1. Introduction

If all other players in a strategic interaction are payoff-maximizers, a player can increase its payoff by committing to maximize something other than its payoff. This paradoxical proposition was proved for a broad class of games by Heifetz et. al. in their provocatively titled paper “What to maximize if you must?” (2007) The proposition implies that, if profit-seeking players are allowed to choose what to maximize, they generally will not choose to maximize profit. This finding brings into question the validity of many applications of game theory which neglect to consider the possibility that players may commit to pursue something other than the payoffs. In the context of strategic management, this implies that we cannot presume on a priori grounds that firms in an oligopolistic industry explicitly and directly pursue profits. Rather, we should expect firms in an oligopoly to commit to pursue revenue, market share, or some other performance metric. We should also expect such firms to exert effort to make their commitments credible and observable.
　The argument for why firms in an oligopoly have incentive to commit to maximize something other than profit has been reviewed by Fershtman and Judd (1987), who also analyzed the ramifications using a model of Cournot duopoly. Since then, strategic deviations from profit maximization have been studied in the context of Cournot oligopoly by Blinder (1993), Dufwenberg and Guth (1999), Gehrig et. al. 【134 頁】 (2004), Miller and Pazgal (2002) and others. The goal of this paper is to simplify the earlier findings to the bare essentials, clarify the key issues, and qualify the argument by considering feasibility constraints from a management perspective.
　In the next section we will informally review why small-numbers competition among profit-seeking firms inherently generates incentives for them to commit to pursue an objective other than profit. Section 3 will apply the theory to a Cournot duopoly with constant unit costs, the simplest context that exposes the key issues. We will then narrow the focus by introducing feasibility constraints in Section 4 and further discuss feasibility from the management perspective in the concluding Section 5.

2. Why maximize something other than profit

A credible commitment by a player in a strategic interaction can influence the behavior of another player in a way that benefits the first player. A firm that builds a large and efficient factory makes a commitment to manufacture more products at a lower cost, and this may induce a competing firm to cancel plans to build a large factory of its own, resigning to a smaller share of the market, or perhaps even exit the market. A much less tangible and often overlooked form of commitment is the adoption of a management philosophy to pursue some performance metric other than profit, for example, revenue or market share. Just like building a factory, a commitment to a management philosophy can also influence the behavior of rivals in a way that benefits the firm that makes the commitment. In equilibrium, all firms may commit to management philosophies and the resulting effect on profits may be positive or negative.
　A number of general treatments have examined endogenous strategic choice of objective function. The conclusions are broad, general, and have support in evolutionary theory. Heifetz, et. al. (2007) formally demonstrated that players in a generic game have incentive to commit to maximize something other than the payoffs of the game. Moreover, they showed that such commitments do not disappear under evolutionary dynamics. Evolution of preferences theory too has shown that agents who maximize a “subjective utility” different from actual payoffs can evolve and displace agents who maximize actual payoffs (Guth and Kliemt, 1998). Winter et. al. (2009) corroborated these findings in their analysis of “mental equilibria.” A critical assumption underlying all these results is that players’ commitments are credible and can be observed by other players with enough precision. We will return to the issue of commitment in later sections.
　These results imply that there are no a priori grounds for presuming that optimizing entities engaged in strategic interactions do best by pursuing payoffs as directly and objectively as possible. On the contrary, the results suggest we should expect optimizing entities in strategic interactions to maximize something other than what they ultimately seek, and, moreover, strive to credibly communicate their commitment to maximize that something else.

3. Commitment to a performance metric in Cournot duopoly

Consider a Cournot duopoly facing linear demand p = a − q₁ − q₂ , where p is the market-clearing price, a > 0 is a demand parameter, and q_i is the quantity of output produced by firm i ∈{1, 2}. Firms 【135 頁】 have constant unit costs c_i. We assume 0 ≤ c₁ ≤ c₂ and a > 2c₂-c₁, which ensures that both firms produce positive quantities in the Cournot-Nash equilibrium. Each firm may adopt a “management philosophy” that observably and credibly commits it to maximize a specific performance metric. All quantity produced by the duopoly is sold at the market-clearing price, giving firms revenue R_i = (a − q_i − q_j ) q_i and profit π_i = (a − q_i − q_j − c_i ) q_i . All of the above is common knowledge.
　We will study equilibrium choice of management philosophies and their effects on profitability using the following two-stage model. In Stage I, firms simultaneously, publicly, and credibly commit to a management philosophy. Specifically, firm i commits that in Stage II it will maximize a “performance function” θ_i (q_i , q_j^E, c_i , c_j , a), where q_j^E is the conjecture by firm i about the quantity to be produced by firm j . Stage II is standard Cournot competition except that each firm seeks to maximize its chosen performance function rather than profit. That is, in Stage II firms simultaneously choose quantities q_i per

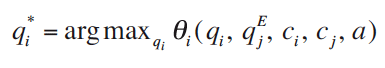
and in equilibrium conjectures about rivals’ output are fulfilled: q_i^E = q_i^*.
　The baseline case is when both firms commit to simply maximize profit. Thus, if both firms choose θ_i = π_i in Stage I, standard Cournot-Nash equilibrium quantities and profits result in Stage II:

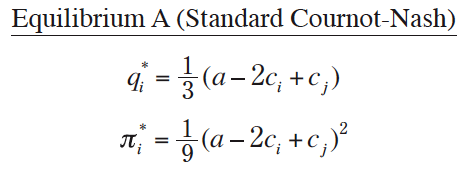
Next suppose each firm may commit to estimate demand optimistically or pessimistically by a bias ω_i . That is, the performance function firms commit to maximize is:

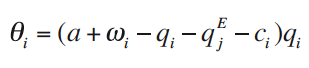
Maximization of this performance function in Stage II by both firms gives the equilibrium quantities as a function of the biases:

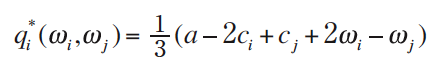
In Stage I each firm looks ahead to Stage II and chooses the bias that will give it the most profit, assuming the rival does the same:

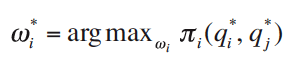
The biases chosen in equilibrium of Stage I are

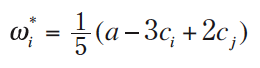
and the resulting quantities and profits are:

【136 頁】

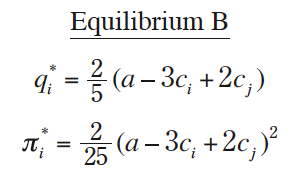
Equilibrium B also results when firms commit to use optimistic or conservative estimates of their costs. Specifically, if each firm estimates its unit cost as c_i − ω_i , then the performance function is again θ_i = (a + ω_i − q_i − q_j^E − c_i ) q_i and therefore the equilibrium biases, quantities, and profits are also the same as above.
　Equilibrium B also results when firms commit to pursue both profit and output. Specifically, if each firm commits to maximize θ_i = π_i + ω_i q_i , then the performance function again takes the form θ_i = (a + ω_i − q_i − q_j^E − c_i ) q_i and therefore the equilibrium biases, quantities, and profits are the same as above.
　Equilibrium B also results when firms commit to pursue both profit and revenue. Specifically, if each firm commits to maximize θ_i = π_i + ω_i R_i , then the performance function takes the form

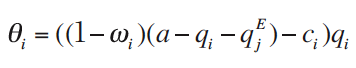
Maximization of this performance function in Stage II by both firms gives the equilibrium quantities as a function of the biases:

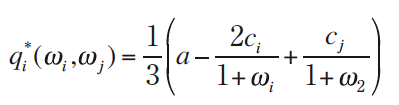
Optimization in Stage I to maximize profit gives the equilibrium biases:

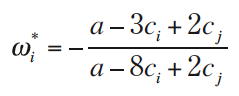
It is straightforward to confirm that the resulting quantities and profits are the same as in Equilibrium B.
　As summarized in Table 1, several different management philosophies result in Equilibrium B. In general, a sufficient condition for a management philosophy to result in Equilibrium B is for the performance function to have the form θ_i = π_i + ω_i f_i (q_i , q_j^E, a, c_i , c_j ), where the function f_i is such that the first-order condition ∂π_i /∂q_i = −ω_i∂f_i /∂q_i can be expressed as ∂π_i /∂q_i = g (ω_i , a, c_i , c_j ) for some wellbehaved function g. An example of a management philosophy which does not meet this criterion is a performance function that incorporates concern for market share: θ_i =π_i +ω_i q_i /(q_i + q_j ). This leads to an essentially different maximization problem whose equilibrium is much less tractable.

Comparing firms’ performance in Equilibrium A and Equilibrium B reveals that the adoption of management philosophies results in:
　■ more output by the more efficient firm 1
　■ more or less output by the less efficient firm 2
　■ possibility of firm 2 shutting down
　■ more industry output and lower market price

【137 頁】

　■ higher or lower profit for firm 1
　■ lower or zero profit for firm 2

Overall, management philosophies intensify competition and may even hurt the profit of the more efficient firm. These conclusions do not critically depend on the assumption that the firms’ products are prefect substitutes. An n-firm oligopoly model that allows for various degrees of strategic substitutability or complementarity reached qualitatively similar conclusions (Gehrig et. al., 2004) In that model, each firm could commit to use a biased estimate of the degree of substitutability or complementarity of its product vis-à-vis products sold in the same market by other firms. In equilibrium, firms committed to over-estimate substitutability or under-estimate complementarity, leading them to compete more aggressively in the output market and earn lower profits.
　Our assumption of constant unit costs is also not critical to the overall conclusions. In a Cournot duopoly where costs increase quadratically with output, Dufwenberg and Guth (1999) allowed firms to commit to maximize a linear combination of profit and output and found that in equilibrium firms do make such commitments and end up competing more aggressively, resulting in lower price, higher output, and lower profits.
　Lastly, our conclusions do not critically depend on the assumption of certainty about costs and demand. Fershtman and Judd (1987) allowed firms to commit to maximize a linear combination of profit and revenue in a Cournot duopoly under conditions of cost and demand uncertainty. In the equilibria of their model, firms commit to place some weight on revenue rather than just pursue profit and end up competing more aggressively, driving down both price and profits.

4. Feasible commitments in Cournot duopoly: profit or revenue

We have been tacitly assuming that firms can fine-tune their management philosophies by choosing from a large space of performance functions parameterized by ω_i . Considering that firms must not only choose a performance function but also explain and commit to the corresponding management 【138 頁】 philosophy both internally and externally, and then actually implement it within the organization, the set of feasible performance functions is probably very limited. In the context Cournot oligopoly, the two simplest and therefore most feasible performance functions are profit and revenue. Therefore, we will next restrict choice of management philosophies to either profit or revenue. Specifically, we will study the following simplified version of two-stage game that we introduced in the previous section:

Stage I: each firm simultaneously, publicly, and credibly chooses to commit to maximize either Profit or Revenue; i. e., each firm chooses performance function θ_i ∈ {π_i , R_i }
　Stage II: each firm simultaneously chooses a quantity that maximizes the performance metric it selected in Stage I, taking into account that its rival is also maximizing its chosen performance function

If both firms choose Profit in stage I, the result is the standard Cournot-Nash Equilibrium A. If both firms choose Revenue in stage I, it is straightforward to show that equilibrium quantities and profits in stage II are

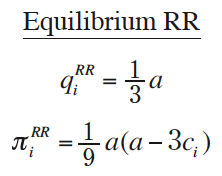
Note that since both firms ignore their costs when choosing quantities, each form chooses the same quantity. Furthermore, the costs do not affect equilibrium quantities and only affect profits.
　The last possibility in Stage I is for firm i to choose Revenue and firm j to choose Profit. It is straightforward to show that in the resulting Stage II equilibrium quantities and profits are

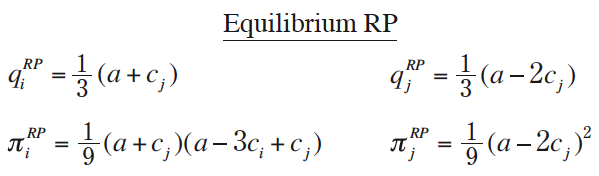
Note that since firm i commits to ignore its cost when choosing quantity, c_i does not affect either firm’s equilibrium quantity or firm j’s equilibrium profit.
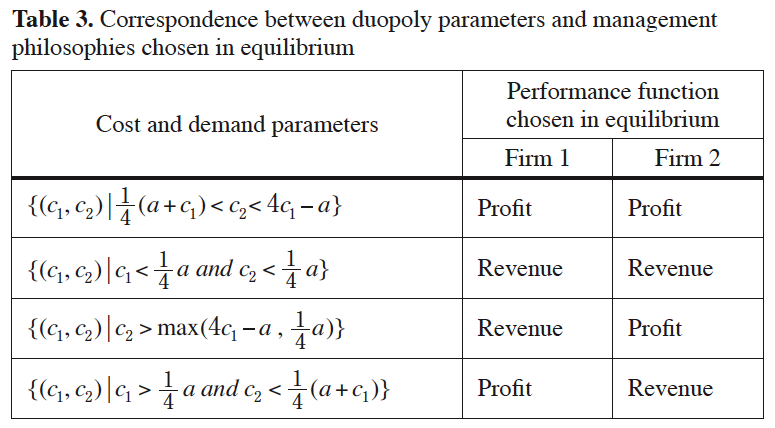
　Profits earned in PP, RR, and RP equilibria comprise the payoff matrix of the Stage I game as shown in Table 2. Each of the four outcomes can be a Nash equilibrium under some combination of cost and demand parameters. Table 3 summarizes conditions on cost and demand parameters that make each outcome a Nash equilibrium. Figure 1 plots the corresponding regions in the space of all possible duopolies parameterized by firms’ costs (c₁, c₂ ).

【139 頁】

Examining the above results leads to the following conclusions about how the possibility of commitment to pursue revenue instead of profits affects firms’ performance:

1. Both firms maximize profit (region AZC in Figure 1): When both firms’ costs are high, neither firm makes use of the revenue-maximizing management philosophy. Standard Cournot Equilibrium A obtains.

2. Both firms maximize revenue (region XFB in Figure 1): When both firms’ costs are low, both firms commit to act as if unit costs were zero and maximize revenue. Compared to standard Cournot equilibrium A, in equilibrium RR firm 1 and industry as a whole earn less profit. Firm 2’s profit is also lower except for a limited set of duopolies satisfying {(c₁, c₂) | a (c₂ − 2c₁) > (2c₂ − c₁)²}. Thus, even though committing to maximize revenue intensifies competition relative to when firms maximize profit, it is possible for the less efficient firm to benefit. This is because if both firms commit to maximize revenue, firm 2’s cost disadvantage becomes irrelevant for choosing quantity, and thus both firms end up on equal footing.

【140 頁】

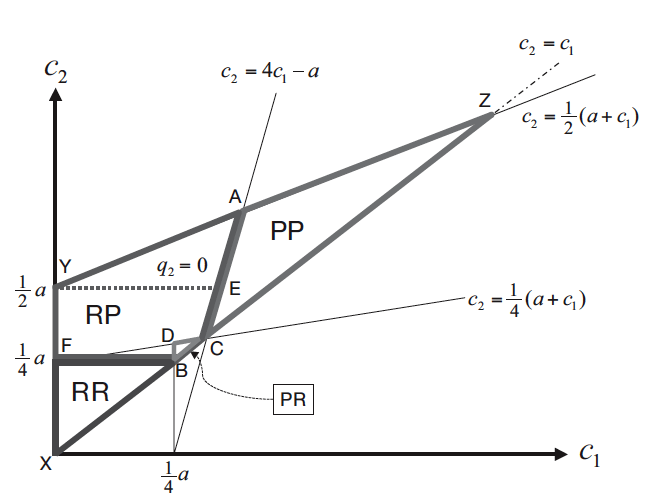
Figure 1　Triangle XYZ is the space of all duopolies such that c₂ ≥ c₁ and q₂^* ≥ 0 when both firms maximize profit. Equilibrium management philosophies are denoted by PP (profit maximization by both firms, region AZC), RR (revenue maximization by both firms, region XFB), RP (revenue-maximization by firm 1, profit-maximization by firm 2, region FYACB), and PR (profit-maximization by firm 1, revenue-maximization by firm 2, region BDC).

3. Firm 1 maximizes revenue, firm 2 profit (region FYACB in Figure 1): When firm 1 is much more efficient than firm 2, there is a Nash equilibrium in which firm 1 commits to maximize revenue while firm 2 maximizes profit. Relative to Equilibrium A, in Equilibrium RP firm 1 earns more profit and firm 2 earns less. Indeed, by adopting the revenue-maximization philosophy, firm 1 may cause firm 2 to shut down completely; this occurs if 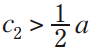, which corresponds to region YAE in Figure 1. Industry profit is higher if 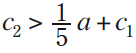; otherwise it is lower.

4. Firm 1 maximizes profit, firm 2 revenue (region BDC in Figure 1): For a small subset of parameter values for which [Revenue, Profit] is an equilibrium, the opposite configuration of philosophies also constitutes a Nash equilibrium. A coordination problem appears in which each firm prefers to adopt a philosophy different from that of its rival. Compared to Equilibrium A, in the [Profit, Revenue] equilibrium firm 2’s profits are higher whereas the profits of firm 1 and the industry as a whole are lower.

The [Revenue, Profit] equilibrium has also been studied by Blinder (1993), who was interested in analyzing competition between a revenue-maximizing firm and a profit-maximizing firm. Blinder concluded that the revenue-maximizer has strategic advantage over the profit-maximizer. However, in 【141 頁】 Blinder’s model firms have identical costs, one firm is exogenously assumed to maximize revenue, and the other profit. Allowing for cost differences and endogenizing each firm’s decision whether to maximize profit or revenue, our model identifies parameter ranges within which Blinder’s conclusions are valid.

5. Discussion

The business press regularly reports about companies pursuing revenue, market share, or some other performance metric, even to the point of sacrificing profit. The theory we have reviewed suggests one explanation for why such pursuits makes strategic sense. But because the theory hinges on the firms’ ability to make public and credible commitments to their chosen performance metrics, the explanation is incomplete without understanding how the firms make such commitments. One possibility is that the commitments are rooted is the institutional environment within which firms operate. For example, the law and norms governing firms’ relations with employees and shareholders are such that employee welfare enters the objective function of many Japanese firms to a greater extent than in the case of American firms (Aoki, 1988). Starting with this observation, Blinder (1993) showed that a firm which includes employee welfare along with profit in its performance function essentially becomes a revenue-maximizing entity. Similar to our findings in the RP equilibrium of Section 4, Blinder showed that such commitment to maximize revenue gives the prototypical Japanese firm a competitive advantage vis-à-vis the prototypical American firm.
　Other ways for a firm to commit to pursue something other than profit have been studied under the rubric of strategic delegation. Strategic delegation models consider a principal (firm owner) who hires an agent (manager) to operate the firm. In one strand of strategic delegation literature, the owner hires a wealth-maximizing manager under an incentive contract that compensates the manager according to some combination of performance metrics, including those that measure performance relative to competitors. Taking this approach, Fershtman and Judd (1987) showed that “profit-maximizing owners will almost never tell their managers to maximize profits.” In another strand of the strategic delegation literature, the owner selects a manager with certain personality traits, such as compulsion to outdo competitors (Miller and Pazgal, 2002) or undue optimism about research and development prospects (Englmaier, 2011). In both strands of strategic delegation literature, commitment to maximize something other than profit is rooted in the psychology of the manager, who is either rationally maximizing his private wealth per his incentive contract or irrationally pursuing goals as dictated by his overly rivalrous or unduly optimistic personality.
　The conclusion is that to earn maximum possible profit, a firm does not necessarily have to pursue maximum profit all the time at every level. A firm which is not overtly pursuing the “bottom line” is not necessarily guilty of poor management, neglect of shareholder interests, or anticompetitive machinations. Rather, our theoretical review indicates that quite the opposite is true: strategic deviations from profit maximization are inherent to the logic of competition in oligopolistic industries. It is a task of strategic management to discover, commit to, promulgate, and maximize performance metrics which ultimately yield maximum possible profits, all while taking into account the performance metrics that rivals have 【142 頁】 committed to pursue. The feasibility of a performance metric critically depends on the ability to credibly commit to use the metric and communicate about it. Contractual, institutional, and psychological bases of commitment can be of use.

References

M. Aoki (1988) Information, Incentives and Bargaining in the Japanese Economy, Cambridge University Press, Cambridge.

A. Blinder (1993) “A simple note on the Japanese firm” Journal of the Japanese and International Economies 7:3, 238-255.

M. Dufwenberg and W. Guth (1999) “Indirect evolution vs. strategic delegation: a comparison of two approaches to explaining economic institutions” European Journal of Political Economy 15, 281-295.

F. Englmaier (2011) “Commitment in R&D tournaments via strategic delegation to overoptimistic managers” Managerial and Decision Economics 32:1, 63-69.

C. Fershtman and K. L. Judd (1987) “Equilibrium incentives in oligopoly” American Economic Review 77:5, 927-940.

T. Gehrig, W. Guth, and R. Levinsky (2004) “The commitment effect in belief evolution” Economics Letters 85, 163-166.

W. Guth and H. Kliemt (1998) “The indirect evolutionary approach: bridging the gap between rationality and adaptation” Rationality and Society 10(3), 377-399.

A. Heifetz, C. Shannon, Y. Spiegel (2007) “What to maximize if you must” Journal of Economic Theory 133, 31-57.

N. Miller and A. Pazgal (2002) “Relative performance as a strategic commitment mechanism” Managerial and Decision Economics 23, 51-6.

E. Winter, I. Garcia-Jurado, J. Mendez-Naya, L. Mendez-Naya (2009) “Mental equilibrium and rational emotions” Discussion Paper 521, Center For The Study Of Rationality, The Hebrew University of Jerusalem.