�y85 �Łz
�o�c���w����@�ɂ����鉉㈐��_�Ɋւ���l�@
���c�@�R����1
�v�|
��X�́C�o�c���w����ɂ����鐄�_�̏d�v���������C�u�`�ɂ����Ă��C��㈉ߒ�����@�v�����O���t�Ƃ��Ċw���ɒ��C���_�͗{����ڕW�Ƃ��Ă����B�{�e�ł́C�o�c���w�̖���@�ɂ����āC�ǂ̂悤�Ȑ��_���s���Ă��邩���C����������Ȃ���_����B��X�́C���̐��_�́C���m������n�܂�C�^����ꂽ�f�[�^�̕����Ɍ������Ă���C�܂�t�����ɐ��_���Ȃ���Ă���ƍl�����B�܂��C���̉ߒ��ɂ����āC�w�K�҂̓A�u�_�N�V�����ɂ�蕔���ڕW��ݒ肵�Ă���ƍl�����B���̍l���Ɋ�Â��C�w�K�x���V�X�e���ɂ����āC�����������������w�K�҂̐��_���x������@�\���ǂ̂悤�Ɏ������Ă�������_����B
�P�D�n�߂�
��X�́C�o�c���w����ɂ����鐄�_�̏d�v���������C�u�`�ɂ����Ă��C��㈉ߒ�����@�v�����O���t�Ƃ��Ċw���ɒ��C���_�͗{����ڕW�Ƃ��Ă����B�����āC��@�v�����O���t��`���c�[���Ƃ��āC��@�v�����O���t�E�W�F�l���[�^���J�����C��@�v�����O���t�����ނƂ��đ����쐬���C����ɗp���Ă����m�P�n�B�{�e�ł́C�o�c���w�̖���@�ɂ����āC�ǂ̂悤�Ȑ��_���s���Ă��邩���C����������Ȃ����������B��X�̏����ڕW�́C�w�K�x���V�X�e���ie-Learning �V�X�e���j�ɂ����āC���x�Ȑ��_�x���@�\���������邱�Ƃł���B���̂��߂ɂ́C�l�Ԃ̊w�K�҂��ǂ̂悤�ɐ��_���s���Ė��������Ă��邩�C�l�@����K�v������B
�@���߂ł́C���_�̂����̂R��ށC��㈁C�A�[�C�A�u�_�N�V�����ɂ��Đ�������B��R�߂ł́C�o�c���w����@�ߒ��ɂ��ĕ��͂��C�����ōs���Ă��鐄�_�ɂ��Ẳ�X�̍l�����C��̓I�Ȍo�c���w����p���Đ�������B��S�߂ł́C�֘A�����Ƃ��āC�|���A�̔����I�����ɂ��ďq�ׂ�B��T�߂ł́C�o�c���w�̂��߂̊w�K�x���V�X�e���ɂ����āC���_���x������@�\�ɂ��Ę_����B�Ō�̏͂́C�܂Ƃ߂ƍ���̌������j�ł���B
�Q�D�R��ނ̐��_
���_�iinference, ���邢��reasoning�j�Ƃ́C�������̑O��i���m�̂��́j����C������
�y86
�Łz
�O��������ɂ��Ă��錋�_�i���m�̂��́j�o����C�_���I�ɓ������ꂽ�v�l�ߒ��ł���B
�@���_�ɂ́C��㈁C�A�[�C�A�u�_�N�V�����̂R��ނ�����C�����́C�ȉ��̂悤�ɕ��ނ����m�Q�n�F
�@�@���_inference
�@�@�@�@�@���͓I���_�ianalytic inference�j
�@�@�@�@�ia�j�@��㈁ideduction�j
�@�@�@�A�@�g���I���_�iampliative inference�j
�@�@�@�@�ib�j�@�A�[�iinduction�j
�@�@�@�@�ic�j�@�A�u�_�N�V�����iabduction�j
�@��㈂ł́C�O������C�_���w�̋�����K���ɏ]���Č��_�o����B�^�Ȃ�O��́C�K�R�I�ɐ^�Ȃ錋�_���������B�O�^�łȂ��ꍇ�C���_���^�ł���Ƃ͌���Ȃ��B�R�i�_�@�́C��㈂ł���B��㈂͘_���I�ɉ��肵���闝�z��Ԃ��`���I�ɐ}���I�ɕ\�ӂ��C���̗��z��Ԃɂ����鎖�ہi�_���I�Ώہj�̊Ԃ̕K�R�I�W����������L���ߒ��ł���m�R�n�B
�@���w�̗�Ō����ƁC�A���������������ĉ������߂�ߒ��́C��㈂ł���m�R�n�B���߂������m���i���_�j�́C�^����ꂽ���Ɋ��ɈÁX���Ɋ܈ӂ���Ă��āC�A���������������`���I�葱���ɂ���āC���m����������邩��ł���B�p�ꂪ����킵�����̂Ƃ��Đ��w�I�A�[�@������B���w�I�A�[�@���C�A�[�@�Ƃ������̂ł͂��邪�C�A�[�I���_�ł͂Ȃ��C��㈓I���_�ł���m�S�n�B�O������C�_���w�̋�����K���ɏ]���Č��_�o���邩��ł���B�����C�A�[�ł́C�X�̌o���I�Ȏ�����W�߁C��������C��ʓI�Ȍ��_����C�Ɉ����o���m�S�n�B�A�[�͈�ʉ��̕��@�Ƃ�������B
�@�A�u�_�N�V�����́C�p�[�X�iCharles Sanders Peirce�j�������B�p�[�X�̓A�u�_�N�V�����̐��_�`�����C�ȉ��̂悤�ɒ莮�����Ă���m�R�n�F
�@�����ׂ�����C ���ώ@�����C
�@����������H ���^�ł���CC �͓��R�̎����ł��낤�C
�@����āCH ���^�ł���ƍl����ׂ����R������B
�@C �Ƃ́C��X�̋^�O�ƒT���������N��������ӊO�Ȏ����܂��͕ϑ����̂��Ƃł���CH ��C��������邽�߂ɍl����ꂽ�����ł���B
�@����g���āC�A�[�ƃA�u�_�N�V�����̈Ⴂ���������B
�@�I���E�[�^���̓o�i�i���D���ł���B�e���O�U���̓o�i�i���D���ł���B�j�z���U���̓o�i�i���D���ł���B���̂R�̎�������C�T���̓o�i�i���D���ł���C�Ƃ������������邱�Ƃ͋A�[�ł���B�A�[�ɂ����ẮC�O�^�ł����Ă����_�͋U�ł���ꍇ������B����ɑ��C�{���l�IX�i�Ƃ������z�̐V�퐶���j�̓o�i�i���D���ł���C�Ƃ��������ׂ�����C ���ώ@���ꂽ�Ƃ��āC���̗��R�Ƃ��āC�{���l�IX �̓T���ł���C�Ƃ�������H ��ݒ肷�邱�Ƃ́C�A�u�_�N�V�����ł���B�A�u�_�N�V�����ɂ����Ă��A�[�@�Ɠ��l�ɁC�O�^�ł����Ă������͋U�ł���ꍇ������B
�@�A�[���A�u�_�N�V�������Ƃ��ɁC�����Ɋւ�邪�C�A�u�_�N�V�����ɂƂ��Ă̎����͋����ׂ��ӊO�Ȏ���C �ł���C�����������邽�߂̗��_H �̒�Ă𑣂��悤�Ȏ����ł���B�������A�[�ɂƂ��Ă̎����́C�A�u�_�N�V�����ɂ���Ċ��ɒ�Ă��ꂽ�����������I�Ɍ����邽�߂ɋ��߂��鎖���ł���m�R�n�B
�@���ۂ̌o�c���w����@�ɂ����鐄�_�̎�ނƂ͉����C���߂ł́C��̓I�����g���Ă���
�y87
�Łz
���l�@����B
�R�D�o�c���w����@�ߒ�
�o�c���w�̖��̖w�ǂ́C�ؖ����ł͂Ȃ��C���m���̒l���i�v�Z�j����^�C�v�̖��ł���B����āC�����̖��ɂ����ẮC���ŗ^����ꂽ�f�[�^�iGiven Data�j���牉㈂����邱�ƂŁC���ʂƂ��āC���m���iUnknown�j�̒l�����߂�B���߂������m���́CGiven Data �␔�w�����C����ьo�όo�c�̃Z�I���[�ɈÁX���Ɋ܈ӂ���Ă���B��������CGiven Data�C�����C�Z�I���[��O��Ƃ��āC��㈂��s���CUnknown �����_�Ƃ��ē��o�\�C�ƌ�����B
�@Given Data ����Unknown �ɓ��鉉㈉ߒ���}�I�ɕ\�������@�Ƃ��āC��X�͐}�P�̂悤�ȕ\�����Ă����B���̉�㈉ߒ�����X�͉�@�v�����O���t�ƌĂ�ł���m�P�n�B�����������Ƃ���ہC��X�͎n�߂���C��@�v�����O���t�̂悤�ȉ�㈉ߒ������ɕ����Ԃ킯�ł͂Ȃ��B�A�u�_�N�V�����ɂ���āC��㈉ߒ��̓r���r���ɂ����ĉ�����n�����C���̉������b��I�ɍ̑����邱�ƂŁC�X�e�b�v�ɕ����Đ��_���s���ƍl������B���̍ۂɂǂ̂悤�ȃX�e�b�v���������邩�C����͂Ȃ��B��X�́C�l���o�c���w�����������_�ߒ��͈ȉ��̂悤�Ȃ��̂ł���ƁC�l�����F
�@�o�c���w�����������߁C�l�́C��㈁C�A�[�C�A�u�_�N�V�����̂��ׂĂ��I�ɋ�g���Ďv�l���s���Ă���ł��낤�B���̏ڍׂ͒肩�ł͂Ȃ��B�������Ȃ���C�l�͂��̎v�l�̉ߒ��ɂ����āC�A�u�_�N�V�����ɂ���āC����H �𗧂ĂĈ�����\�����Ȃ���CUnknown ����Given Data �����ɂނ����āC�܂�t�����ɉ�㈐��_��K�����āC�ׂ����X�e�b�v�ɕ����Ė��������Ă���̂ł͂Ȃ����낤���B�A�u�_�N�V�����ɂ���Ē�Ă���鉼��H �Ƃ́C�����̏ꍇ�C�uYY ���v�Z�ł���Ȃ�CXX ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ����`���̉����ł���CYY ��O��Ƃ��āC��㈂ɂ���ĕK�R�I�ɖ��m��XX ���v�Z����邱�Ƃ������B�i��@�v�����O���t�ɂ����ẮCYY �̕�����ʂɈʒu����B�j�����ł́CXX �����܂�C�Ƃ������Ƃ������ׂ�����C �ł���CYY ���v�Z�\�ł���C�Ƃ������Ƃ�����H �ɑΉ�����B���ɁC�uZZ ���v�Z�ł���Ȃ�CYY ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ����������A�u�_�N�V�����ɂ�萄������B���̂悤�Ɏ��X�ƁC�����ڕW��ݒ肷��B���̍ۂɍs���Ă��鐄�_�̎�ނ̓A�u�_�N�V�����ł���B�A�u�_�N�V�����̍ہC�����̉��݂̒�����C�ł������Ƃ��炵��������I�Ԃ��Ƃ��d�v�ł��邪�C����́C���̎��_�ŗ^����ꂽ�f�[�^�ƌv�Z�ς݃f�[�^�C����сC�m���Ă����������уZ�I���[����g���Đ�������B
�@��X�̍l�����̃|�C���g�́C�t�����ɐ��_����C�Ƃ����_�ƁC�A�u�_�N�V�����ɂ�蕔���ڕW��ݒ肷��C�Ƃ����_�ł���B�l�����̂悤�ɐ��_����Ɖ��肵���ꍇ�Ce-Learning �V�X�e���\�z�ɂ����Ă��C���̃v���Z�X���w���v����悤�ȋ@�\����������C�w���̊w�K�Ɍ��ʂ�����̂ł͂Ȃ����낤���B
�@��ʓI�ɉ����I���͂ǂ̂悤�ɍs���Ă���̂��B�p�[�X�͉�����I������ۂɁC�A�u�_�N�V�������]��Ȃ��Ă͂Ȃ�Ȃ��ȉ��̏����������Ă���m�Q�n�F
�i�P�j �����Ƃ��炵���iplausibility�j: �����͌������̖��̌��ۂɂ��āC�����Ƃ��炵���C�ł����ɂ��Ȃ���������^������̂łȂ��Ă͂Ȃ�Ȃ��B
�i�Q�j ���؉\���iverifiability�j: �����͎����I�Ɍ��؉\�łȂ��Ă͂Ȃ�Ȃ��B
�y88 �Łz
�i�R�j �P�����isimplicity�j: �������x�̐����\�͂�L���邢�����̉���������Ƃ���ƁC���P���ȉ�����I�Ȃ��Ă͂Ȃ�Ȃ��B
�i�S�j �o�ϐ��ieconomy�j: �P���ȉ����قǁC����������I�Ƀe�X�g����̂ɔ�p�⎞�Ԃ�v�l��G�l���M�[���ߖ�ł��邩��C�P���ȉ�����I�Ȃ��Ă͂Ȃ�Ȃ��B
��L�i�S�j�ɂ��āC���w�҃W���[�W�E�|���A�iGeorge Pólya�j�m�T�n���C���w�Ƃ�������ɂ����āC�������Ƃ������Ă���B�|���A�́C�������������̂ɁC�m���Ă��邩��ƌ����āC����e�N�j�b�N����g���ĉ��������C�ȒP�ɉ�������@��I�����ׂ��ł���C�ƌ����Ă���m�U�C�V�n�B
�@�ȉ��C��X�̍l����������邽�߂ɁC�Q�̋�̓I�ȋ��Z���w�̖����Ɏ�肠����m�W�n�B
���P
�@��X �́C�c���N���Q�N�C�N�[�|���E���[�g2.00�� , �����̉��i�i�z��100�~������j100.00�~�C�}�R�[���[�E�f�����[�V������1.98�N�C�C���f�����[�V������1.94�C�R���x�L�V�e�B5.69�C�N�[�|���̎x�������N�P��̍��ł���B�����̍ŏI�����i�N�P���j��2.00���ł���C�����͗�����������ł���B�X�|�b�g�E���[�g�E�J�[�u�͐����Ɖ��肷��B�����C�X�|�b�g�E���[�g���P���ቺ���āC���̂܂܂P�N�Ԍo�߂����Ƃ���B�����̍����i���C�ߎ������g���ċ��߂Ȃ����B��X �ɍ�������P�N�ԓ��������ꍇ�̓������^�[���͉����ɂȂ�܂����B
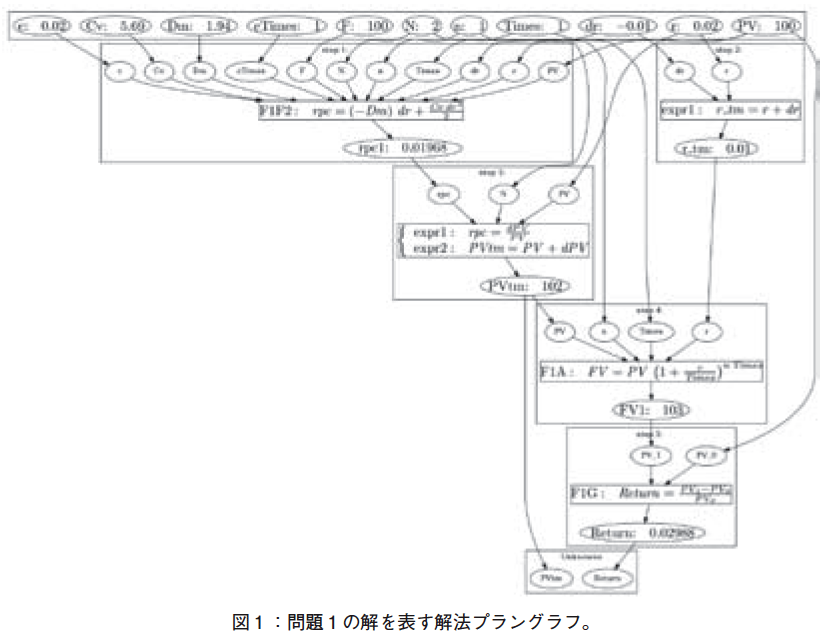
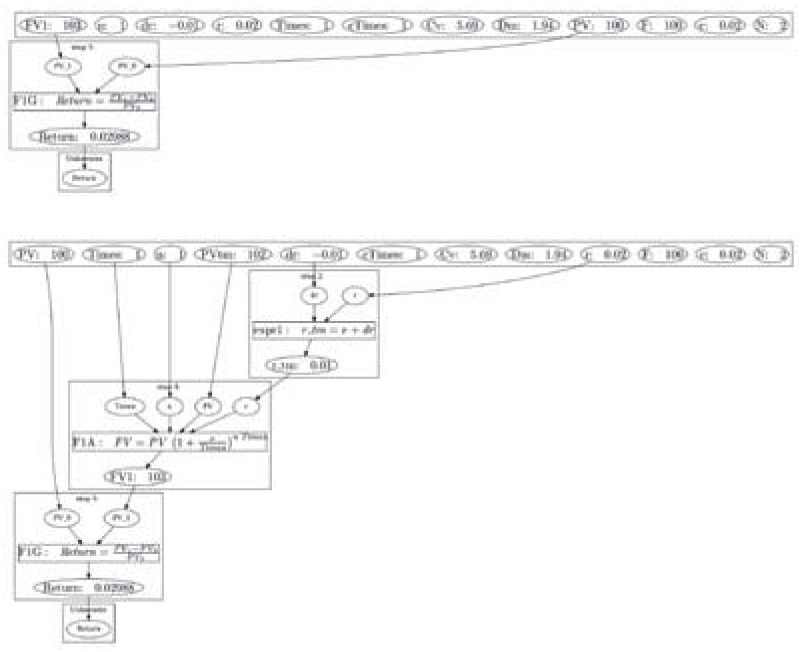
���̖��̉�㈉ߒ��́C�}�P�̂悤�ɕ\�����B���̐}�́C��X���J��������@�v�����O���t�E�W�F�l���[�^�ɂ���č쐬�����B�}�P�ɋL�ڂ���Ă���������ȉ��Ɏ����B

�����̂Ȃ��C�����Ƃ��炵�����_�Ƃ��āC�ȉ��̂悤�ȋt�������_���l������FReturn �����m���ł���̂�����C���̒�`���g�����_���s���Ƃ悢�ł��낤�i�}�P��step�T�j�B���̂��߂ɂ́C�����̍����iPV ����сC�P�N��̏������lFV�P�����߂�K�v������istep�S�j�B
�@�����ϓ��ɂ��C�����Ɩ����̋����i�X�|�b�g�E���[�g�j�̍��́C�P���̒ቺ�ƁC���͂ɋL�ڂ���Ă���B�����ŁC�u�����̍����iPVtm ���v�Z�ł���̂ł���C�P�N��̍��̏������lFV�P���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ������������Ă��邱�Ƃł��낤�istep�S�j�B
�@�u�����Ɩ����̍����i�̍������v�Z�ł���̂ł���C�����̍����iPVtm ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�istep�R�j�B�܂��C�u���i�ω���rpc ���v�Z�ł���̂ł���C�����Ɩ����̍����i�̍����v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�istep�R�j�B
�@�܂�CPVtm �����߂邽�߂ɂ́C���i�̍���dPV ���K�v�ł��邪�C����͉��i�ω���rpc�̌�����p���邱�ƂŌv�Z�����ł��낤�istep�R�j�C�Ɛ�������B����rpc ���v�Z���邽�߂�
�y89
�Łz
�́C����F�PF�Q�̃e�C���[�W�J�̌������g���悢�ł��낤�istep�P�j�B����F�PF�Q��p����rpc �����߂邽�߂ɂ́C�ق����f�[�^PV, Dm, Cv ��������Ă��邩�����ƂȂ�CGivenData���m�F����ƁC�͂����āCPV, Dm, Cv �̒l�͗^�����Ă����B
�@���̂悤�ȋt�����̐��_���s����C�ƍl���邱�Ƃ͂����Ƃ��炵���B���̉�@�ɂ�����C�ł��d��ȂЂ�߂��Ƃ�����ׂ������́Cstep�R�́u���i�ω���rpc ���v�Z�ł���Ȃ�C�����i�̍���dPV ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�ł��낤�B�����̊w�������Ă���ƁC������v�������ۂ����C�����������邩�ۂ��̕���_�ƂȂ�B�����āCrpc ��GivenData ���g���ċ��߂��邩�������C���̌��ʁC���߂��邱�Ƃ������B����āCrpc �����߂�ꂽ�̂ŁC��㈂ɂ���āCdPV �����߂���C�ƂȂ�B
�@����step�P�ɑ������鉼���̐ݒ�ɂ����āC��X�͎��s����I�ɉ������l���Ă���B�������C���̍ۂɂ́C���闝�R�������āC�������鉼���̒�����ł������Ƃ��炵��������I�����Ă���B�Ⴆ�C���͑�Ƃ��āC�C���f�����[�V����Dm ��1.94�C�R���x�L�V�e�BCv 5.69���^�����Ă���̂ŁCrpc �̌��������Ȃ��Ƃ��ǂ����Ŏg���̂łȂ����C�ƁC����l�͐�������ł��낤�B�����̏ꍇ�C�t�����ɐ��_���s���邪�C�t�������@����̂ݐ��_���s����킯�ł͂Ȃ��C���̐l�̉ߋ��̌o���Ȃǂ���C�����ڕW���ݒ肳�ꂤ��̂ł��낤�B����step�P�̐��_�́C�����������ł���B
�@���ɂ����ЂƂ��������悤���͂��Ă݂悤�B
�y90
�Łz
���Q�F
�@�����܂łR�N�C�N�[�|�����T���C�ŏI�����T���̍��̃}�R�[���[�E�f�����[�V���������߂�B���̍��ɓ��������ꍇ�C���̃}�R�[���[�E�f�����[�V�����̊��Ԍo�ߌ�̏������l�͂�����ɂȂ邩�B�ŏI����肪�T���ŕω����Ȃ��ꍇ�ɂ��Čv�Z���Ȃ����B�Ȃ��C�N�[�|�����͍ŏI�����ōē����ł�����̂Ƃ���B
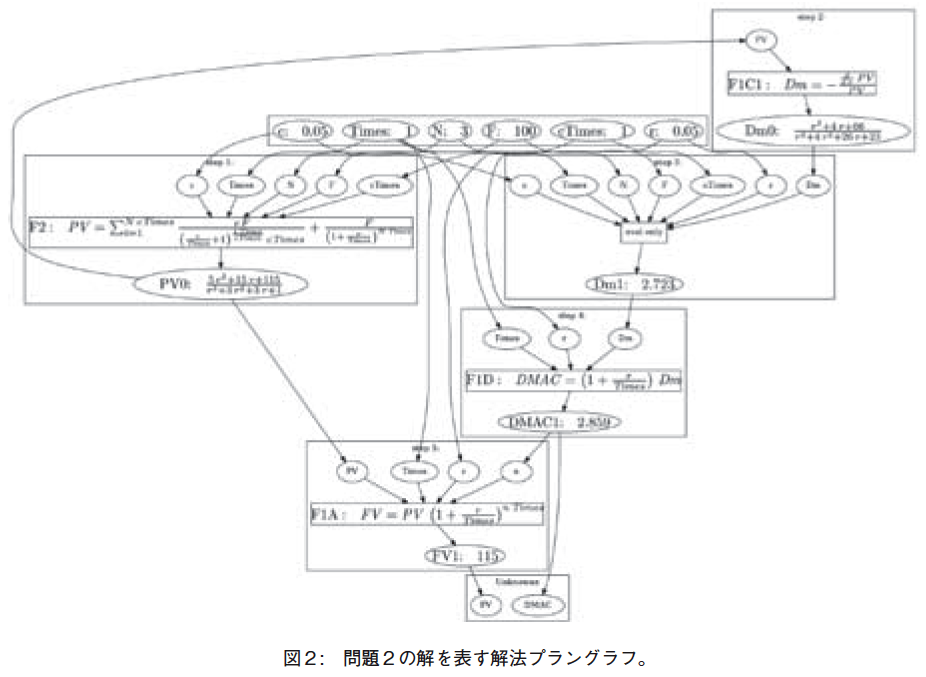
���̖��̉�@�v�����O���t��}�Q�Ɏ����B�����Ŏg���Ă�������͈ȉ��ł���B
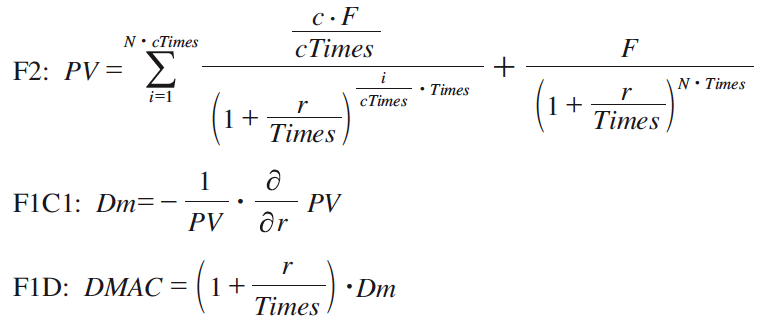
�y91
�Łz
�@���̖��Q�ɂ�����|�C���g�́CStep�T�̂悤�ɁC�uDMAC ���v�Z�ł���̂ł���C�������lFV ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ������������Ă��邱�Ƃł��낤�BDMAC ���o�ߔN��n �Ƃ��āC����F�PA�i�������lFV �̌����j�ɑ�����邱�ƂŁC�������l�����߂���B�m���Ƃ��āCDMAC �̎����̒P�ʂ��C�N�ł��邱�Ƃ�m���Ă���C����ɂ��̐������e�ՂɎv�����ł��낤�B���̃X�e�b�v�Ƃ��ẮuDm ���v�Z�ł���̂ł���CDMAC ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ������������Ă��邱�Ƃł��낤�B���ɁC�uDMAC ���v�Z�ł���̂ł���C�����iPV ���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ƃ������������Ă��邱�Ƃł��낤�B
�@��L���P�ƂQ�̂Q������Ă����B�����ڕW��ݒ肷��A�u�_�N�V�����ɂ����āC�ǂ̂悤�ɉ�����I�����邩�́C�n���I�E�����I��Ƃƌ�����B��㈉ߒ��o����ߒ��ɂ����āC�A�u�_�N�V�����Ɖ�㈂��g���Ă��邱�Ƃ�����������C�A�[�ɂ��Ă��l���Ă݂����B�A�[�́C�m����̌n�Â���ۂɎg����B�Ⴆ�C�}�R�[���[�E�f�����[�V����DMAC �͋����ϓ��ɑ��鉿�i�̊��x�������B�C���f�����[�V����Dm �͋����ϓ��ɑ��鉿�i�̊��x�������B������A�[�ɂ���āC�e��f�����[�V�����͋����ϓ��ɑ��鉿�i�̊��x�������C�ƈ�ʉ�����B
�@�f�[�^�x�[�X�̐��E�ł́C���_�f�[�^�x�[�X�␄�_�G���W���ƌĂ��V�X�e������㈂��s���B���_�G���W���́C�@�B�I�ɉ�㈂��J��Ԃ��C��㈉ߒ��̃p�X��T������m�X�n�B����C�l�Ԃ���㈂��s���ꍇ�́C�@�B�����n���I�ɃA�u�_�N�V�������s���C�p�X�����Ă���Ɗ�������B�p�[�X�ɂ��ƁC�l�Ԃɂ͖{���u��������������\�́v��������Ă���B����āC�l�Ԃ̐��_�͍l����ꂤ�邠���鉼���̒�����C����L����̐����ɂ���Ă����Ƃ��������������l�����Ă邱�Ƃ��ł���C�Ƃ���m�Q�n�B�o�c���w����@�ɂ����Ă��C�A�u�_�N�V�����ɂ�艼����I�������Ƃɂ����āC�l�Ԃ͋@�B�����n���I�ɉ����I�������Ă���C�ƌ�����ł��낤�B���̓_���l�ԂƋ@�B�̍��ł��낤�B
�S�D�|���A�̔����I����
���w�͉�㈂����ɂ���Ă��̌��ʂ̐������𗧏���B��������㈉ߒ������邽�߂ɂ́C��㈂����ł͂Ȃ��C�A�u�_�N�V�����ɂ��n���I�Ȑ������K�v�ł���B���w�̏d�v�Ȓ藝�̔�������C�o�c���w�ʼn�������̃h������艉�K�ɂ�����܂ŁC���ׂẲ�㈉ߒ������ɂ����āC�A�u�_�N�V�������s���Ă���B�A���C���܂�ɒP���ȉ�㈉ߒ��ł悢�ꍇ�́C�A�u�_�N�V�����͍s���Ȃ��B����ł́C���w�҃|���A�́C�A�u�_�N�V�����ɂ��ċC�Â��Ă����̂��B�ȍ~�ł͂���ɂ��Ę_����B
�@���w�҃|���A�́C�ނ̒����w�����ɂ��Ė����������i"HowToSolveIt"�j�x�Ȃǁm�T, 10, 11�n�ɂ����āC�����@�I�i�q���[���X�e�B�b�N�j���n���琔�w�̉�����������Ă���B�|���A�́C�ނ̔����I���_�Ƃ́C�����A�[�Ɨސ��ɂ��ƂÂ��C�ƋL���Ă���m�T�n�B�|���A�̈̑�ȓ_�́C���̔����I�����̕��@��`���邽�߂ɁC���w���t�͂ǂ̂悤�Ɋw�����w�����ׂ����ƁC��̓I���w���������Đ������Ă���_�ł��낤�B���݂ł��C�|���A�̃q���[���X�e�B�b�N�͐��w����̕���ŋ����x������Ă���B
�@�|���A�́C�t�����ɉ����iworking backwards�j�Ƃ��āC�M���V���̐��w�҃p�v�X�iPappus�j�̌��t���Q�Ƃ��Ă���m�T�n�F Let us start from what is required and assume what is sought as already found. Let us inquire from what antecedent the desired result could be derived.
�y92
�Łz
�@��X�̖ڂ̑O�ɂ���o�c���w�̖��ɗ����Ԃ��Ă݂�ƁC�����ʼn�㈐��_�ߒ�������ۂɁC�t�����ɕ����ڕW��ݒ肷��C�Ƃ����������s���Ƃ������Ƃ́C�|���A���t�����ɉ������Ƃɂ����āC�咣���Ă������Ƃƈ�v����B
�@�|���A�̎���ɂ́C�A�u�_�N�V�����Ƃ����l�����͂܂����y���Ă��Ȃ������̂ŁC�|���A�́C���̔����I���_���A�[����їސ��Ƃ��đ����Đ������Ă���B�������C�|���A�́C���w��@�ɂ����锭���I���_�̕��@�́C�]���̋A�[�ł͂Ȃ��C�W�R�I�i�܂�^�ł��邱�Ƃ�����C�����łȂ����Ƃ�����j���_�ł���C�ƋC�Â��Ă����B
�@�Đ��́C�|���A�̔����I�R�i�_�@�́C�A�[�ł͂Ȃ��C�p�[�X�̃A�u�_�N�V�����Ɠ����`���̂��̂ł���C�ƌ����Ă���m�Q�n�B
�@�|���A�̔����I�R�i�_�@�̈�ʓI�`���́C�ȉ��̂悤�Ȍ㌏�m��ł���m�Q�n�F
�@�@����A ����������CB ���܂��������C
�@�@����B �����������Ƃ����������C
�@������CA �����������Ƃ͊m���炵���B
����͌㌏�m��ł���B�㌏�m��͘_���I�ɑÓ��ł͂Ȃ��B�㌏�m��͌��ł���B�Ⴆ�C�ȉ��̌��_�͋U�ł���B
�@�@�@���͉ԕ��ǂɂ������Ă���Ƃ��C�ڂ��Ԃ��Ȃ�B
�@�@�@���C���̖ڂ��Ԃ��B
�@�@�@�����玄�͉ԕ��ǂɂ������Ă���B
���̖ڂ��Ԃ��̂́C���̕a�C��������������Ȃ����C�����Ă��邩�炩������Ȃ��B�㌏�m��́C���ʂ��猴���ւƑk�y���C����A ���b��I�ɍ̑�����B���̂悤�ɁC�b��I�ɍ̑����ꂽ�����̂Ȃ��ŁC�ł����ɓK�����������Ă��邱�Ƃ��A�u�_�N�V�����ł���B
�@�Đ��͌����m�Q�n�F�|���A�͒��ҁw�����ɂ��Ė����������x�m�T�n�̂Ȃ��ŋt�s�I�����Ƃ������t����x�����g���Ă��邪�C�t�s�I�����Ƃ������t�̈Ӗ����C�|���A����ɏq�ׂĂ��锭���I�R�i�_�@�Ɍ��т��čl���Ă�����C�A�[�Ƃ͂܂������Ⴄ�V�������_�̊T�O�ɂ������Ă����̂ł͂Ȃ����B
�@�O�q������X�̍l���́C�|���A�̔����I���_�̂����̋t�����ɍl������@�C�Ƃ����v���Ă���B
�@�o�c���w����@�̉�㈉ߒ������߂邽�߂ɂ́C��㈁C�A�[�C�A�u�_�N�V�����̂��ׂĂ��I�ɋ�g���Ďv�l���s���Ă���ƁC��X�͍l����B���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���āC�����𗧂ĂĈ�����\�����Ȃ���CUnknown ����Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����ƍl����B
�@�������C���镔���ɂ��Ă͑O�������_���s���Ă���ӏ�������ł��낤�B�܂��C�ł����ɓK����������I������ۂɁC�ǂ̂悤�Ȑ��_���s���Ă��邩�́C���G�߂��ĕs���ł���B�������C�S�̂̕��@�Ƃ��āC�u�t�����ɉ�㈐��_��K�����āC���������Ă���v�Ƃ����l���͑����̏ꍇ�������ƍl������B
�T�D�w�K�x���V�X�e���ւ̉��p
�{�߂ł́C�w�K�x���V�X�e���ɂ����āC�w���̉�㈐��_���x������@�\�ɂ��Ę_���Ă���
�y93
�Łz
�����Be-Learning �V�X�e���́C�Ώ̂Ƃ���w�K���e�ɂ���āC�ȉ��̂Q��ނɑ�ʂł���:�i�P�j�m���蒅�̃g���[�j���O�p�C�i�Q�j��勳��ɂ�����m���̓W�J����ѐ��_�Ɏ��������w�K�x���p�C�ł���B�Ⴆ�C�Q����������������K�C�p�P���C�f�B�I���̈ËL�Ȃǂ͑O�ҁi�P�j�ɑ�������B��X�������Ă���o�ρE�o�c���w�͌�ҁi�Q�j�ł���B������̎w�E����悤�ɁC��勳��̂悤�ɒm���̓W�J�Ɏ���u���ȖڌQ�ɂ́Ce-Learning ������܂Ȃ��̂ŁC��勳��ł�e-Learning �V�X�e���̊��p���i�܂Ȃ��B��勳��ł�e-Learning �����p����Ȗڂ�����X���ɂ���m12�n�B���ɁC���_���x������悤�ȋ@�\�́Ce-Learning �V�X�e���Ƃ��ẮC����̌����E�J�������҂���镪��ł���B
�@e-Learning �V�X�e���̗��_�Ƃ��āC�l�̐i���x�ɉ����āC�s������m���v�f�ɑ���e-Learning ���ނ�I�m�ɒ��o���C��蒼�����邱�Ƃ��\�ł���C���Ƃ���������m13, 14�n�D�����āCe-Learning �̕���ł͍L���C�w�K�҂��ԈႦ���Ƃ��ɁC�߂�ׂ������ǂ̂悤�ɑI������̂��C�Ƃ����������L���s���Ă���B��ʓI�ɂ́C�w�K�҂͂ǂ̕��삪�ア����LMS�iLearning Management System�j����c�����C�w�K�ɉ������w�K�w�����s���m15�n�B�������C�o�ρE�o�c���w�̂悤�Ȑ�勳��ɂ����鐄�_���x������悤�ȋ@�\�́C����̌����E�J�������҂���镪��ł���B��Ԃ̗��R�Ƃ��ẮC���_���x�����邱�Ǝ��́C�l�Ԃ̋��t�ł�����_������B�T�@�ŁC��q���C�܂��Ɍ��悤���Ƃ��������ɁC�t�����C���̍D�@���Ԕ�����ꂸ�ɂ��݁C���ɋ�����^���Ē�q�����̋��n�ɓ������Ƃ��C啐�퓯���i���������ǂ����j�ƌ����B��X�̑ΏۂƂ���o�ρE�o�c���w���̕���ł����ƁC�w�����܂��ɃA�u�_�N�V�����ōł������Ƃ��炵���iplausible�j������I�����悤���Ƃ��������ɁC���t���C���̍D�@��c�����C���ɋ�����^���Ċw���̃A�u�_�N�V�������x�����邱�Ƃł���B�w���ւ̎w���́C���̐��_�\�͂̐����̒i�K�ɉ����ēK�X�K�ɍs�Ȃ��K�v������B��X�̖ڎw���w�K�x���V�X�e���ɂ����ẮC�����i�K�ɉ����ēK�Ȏw�����s����C���̂悤�Ȑ��_�x���@�\��ڎw���B啐�퓯���C���邢�́C啐��̋@�Ƃ́C�t���ƒ�q�̊Ԃ̗��z�̋���@��̔�
�g�Ƃ��Ă��g����̂ŁC���̖��O���Ƃ��āC�ȍ~�ł́C��X�̖ڎw�����_�x���@�\���u�\�b�^�N�x���@�\�v�ƌĂԂ��Ƃɂ���B
�@�w������@���v�����Ȃ������ꍇ�C�܂�C��@�v�����O���t�̂悤�ȉ�㈐��_�ߒ��ɕ`���Ȃ������ꍇ�C�\�b�^�N�x���@�\�́C���m������t�����ɁC�A�u�_�N�V�����̕����ڕW��ݒ肷�邱�Ƃ��x������B��̓I�ɂ́C�ł��ʼn��w�ɂ��鉉㈐��_�X�e�b�v�����̃V���v���Ȗ₢���������C����𗝉��ł��邩�ۂ����w���ɖ₤�B
�@�\�b�^�N�x���@�\�̗�Ƃ��āC�O�q�������P���ȒP��������������B
���P���ȒP���������
�@��X �́C�c���N���Q�N�C�N�[�|���E���[�g2.00�� , �����̉��i�i�z��100�~������j100.00�~�C�}�R�[���[�E�f�����[�V������1.98�N�C�C���f�����[�V������1.94�C�R���x�L�V�e�B5.69�C�N�[�|���̎x�������N�P��̍��ł���B�����̍ŏI�����i�N�P���j��2.00���ł���C�����͗�����������ł���B�X�|�b�g�E���[�g�E�J�[�u�͐����Ɖ��肷��B���i�ω�����0.01968�ł���B�����C�X�|�b�g�E���[�g���P���ቺ���āC���̂܂܂P�N�Ԍo�߂����Ƃ���B�����̍����i���C�ߎ������g���ċ��߂Ȃ����B��X �ɍ�������P�N�ԓ��������ꍇ�̓������^�[���͉����ɂȂ�܂����B
�y94 �Łz
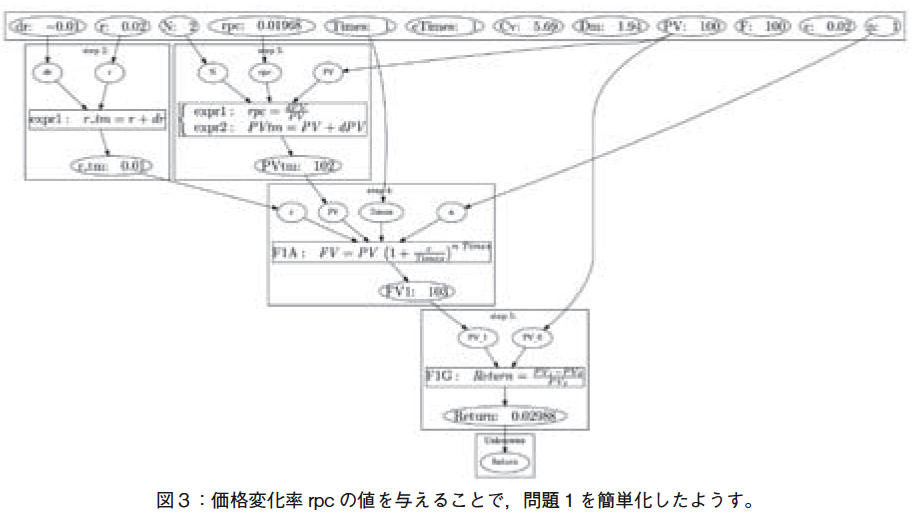
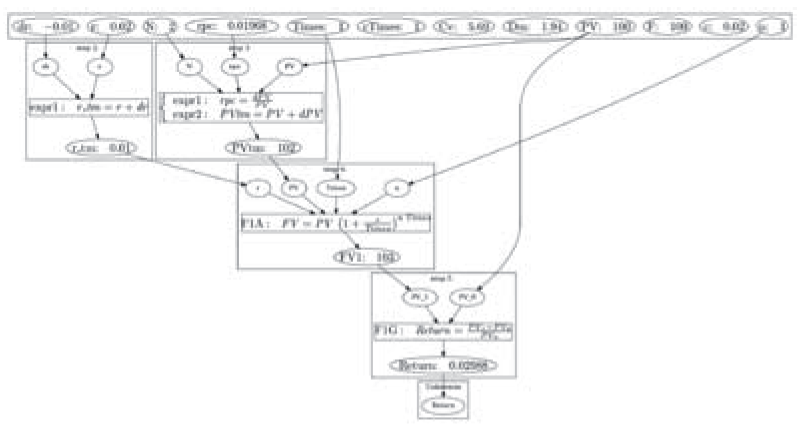
�����ȒP�����邽�߁C���i�ω���0.01968�͒��ŗ^���Ă���B���̖��ɑ����@�v�����O���t�͐}�R�̂悤�ɂȂ�B
�@�}�P�Ɛ}�R�̉�@�v�����O���t���r����B���i�ω���rpc �����͑�ŗ^����ꂽ���ƂŁCstep�P�̉�㈐��_�ߒ��̓X�L�b�v����ĂȂ��Ȃ��Ă���B���̂��߁CGivenData ���ŗ��p����Ȃ������f�[�^���o�Ă���B�}�R�̍ŏ�i�ŁC������cTimes, Cv, Dm, F, c �����p����Ă��Ȃ����Ƃ�������B
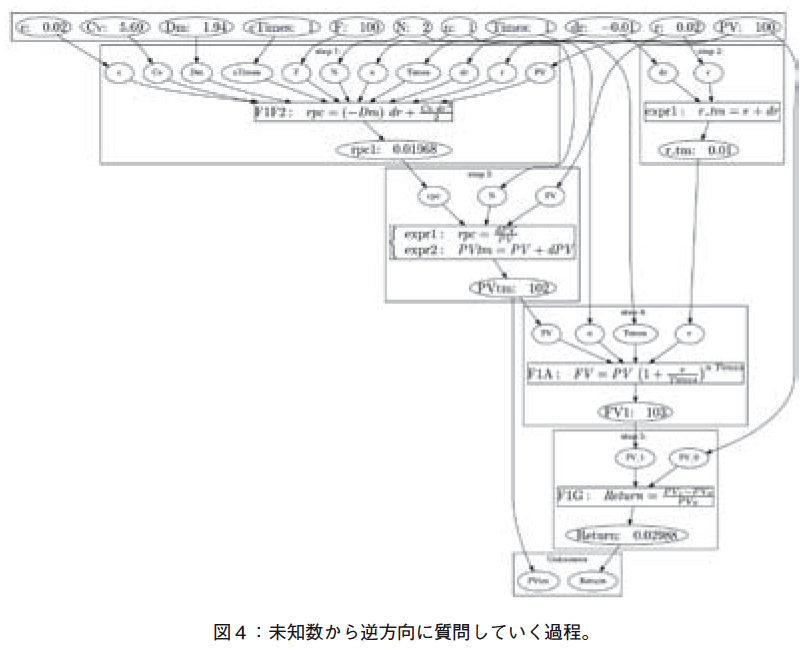
�@�\�b�^�N�x���@�\�Ƃ��ẮC�w���������ł��Ȃ������ꍇ�C�����ł��Ȃ�������㈐��_�ߒ�����肷�邽�߂ɂ��C���m������t�����Ɏ��₵�Ă������j���Ƃ�B���P�̖��m��Return�����߂�ꍇ�̃\�b�^�N�x���@�\�̐������ׂ���@�v�����O���t�S��}�S�Ɏ������B�P�Ԗڂ̉�@�v�����O���t���C�ł��ȒP�����ꂽ����ɑ�������B�ȉ��C���ɓ���Ȃ��Ă����B�}�S�ɁC�����悤�ɁC�n�߂͖��m�����������ݒ�Ƃ��āC�����C����ɏ���։�㈐��_�������L���Ă����B�}�S�Ɏ����悤�ɁC�������C�A�E�g�̂��߁C�e��㈐��_�X�e�b�v�̈ʒu�W������Ă��܂��͎̂d�����Ȃ��B�w�������������Ȃ������ꍇ�C���̂悤�ɊȒP�Ȗ�肩�珇�ɉ������Ă����x���@�\������Ă��������B
�y95 �Łz
�y96 �Łz
�T�D�܂Ƃ�
�o�c���w����@�̉�㈉ߒ������߂邽�߂ɂ́C��㈁C�A�[�C�A�u�_�N�V�����̂��ׂĂ��I�ɋ�g���Ďv�l���s���Ă���ƁC��X�͍l����B���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���āC�����𗧂ĂĈ�����\�����Ȃ���CUnknown ����Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����ƍl����B
�@��X�́C�o�c���w����ɂ����鐄�_�̏d�v���������C�u�`�ɂ����Ă��C��㈉ߒ�����@�v�����O���t�Ƃ��Ċw���ɒ��C���_�͗{����ڕW�Ƃ��Ă����B�����āC��@�v�����O���t��`���c�[���Ƃ��āC��@�v�����O���t�E�W�F�l���[�^���J�����C��@�v�����O���t�����ނƂ��đ����쐬���C����ɗp���Ă����B���̉ߒ��ɂ����āC��㈉ߒ��������Ƃ́C��㈂����ł͂ł��Ȃ��C�ƋC�Â����B�����āC���̔����ɂ́C�p�[�X�̒���A�u�_�N�V�����Ƃ����V�����^�C�v�̐��_���W���Ă���ƍl�����B�����āC�]�����琔�w����̃q���[���X�e�B�b�N�X�Ƃ��đS���E�ɕ��y���Ă���|���A�̔����I���_�̓A�u�_�N�V�����ł��邱�Ɓm�Q�n�C�t�����ɉ�㈐��_��K�����Ė��������Ȃ����C�Ƃ������Ƃ̓|���A���M���V���̐��w�҃p�v�X�̌��t�����p���Ď咣���Ă��邱�Ɓm�T�n���C�ĔF�������B
�y97
�Łz
�@���_���x������悤�ȋ@�\�́Ce-Learning �V�X�e���Ƃ��ẮC����̌����E�J�������҂���镪��ł���B��X�͉�@�v�����O���t�E�W�F�l���[�^��p���āC���_���x������V�X�e�����쐬�������B���̑�P�X�e�b�v�Ƃ��āC���m������t�����ɉ�@�v�����O���t���쐬���C����ɍ��킹�Ċw���Ɏ��������@�\���Ă����B���̐��_�x���@�\���C�T�̗p��u啐�퓯���i���������ǂ����j�v�������āC�\�b�^�N�x���@�\�Ɩ��t�����B�\�b�^�N�x���@�\�́C���̐��_�ߒ����v�����Ȃ��w�����x������B�w���������Ȃ������ꍇ�C�����Ȃ���㈐��_�X�e�b�v����肷�邽�߂ɂ��C���m������t�����Ɏ��₵�Ă������j���Ƃ�B�n�߂͖��m�����������ݒ�Ƃ��āC�����C����ɏ���։�㈐��_�������L���Ă����B����̌������j�Ƃ��ẮC���́u�\�b�^�N�x���@�\�v���w�K�V�X�e����Ɏ������Ă��������B
�@���G�ȉ��X�e�b�v�ɂ��킽�鐄�_�ߒ���K�v�Ƃ��鐔�w���̏ꍇ�C���r���[�ɂ����������Ă��Ȃ��w���́C���鎞�͉����邪�C������肪�ό`�����ƁC�����Ȃ��C�Ƃ������Ƃ��N����B����́C�ǂ̂悤�Ȑ��_���s���Ă��邩�̗������s�\��������ł���B���_�ߒ��m�ɒ��āC���̗������x�����鍂�x�Ȋw�K�x���V�X�e������X�͍\�z���Ă��������ƍl����B
�ӎ�
�w�K�x���@�\�̓��_���C啐�퓯���Ƃ������t���Ă��Ă��ꂽ�É�������a�ꍂ�Z���w���@�����ꎁ�Ɋ��ӂ��܂��B�܂��C������C�L�Ӌ`�ȃA�h�o�C�X����������w�K�@��w�v�Z�@�Z���^�[�v�ێR�N��y�����Ɋ��ӂ��܂��B�{�����̈ꕔ�́C����24�N�x�C�Ȍ����b�����iC�j��ʁu���_�G���W���@�ɂ��m���x�[�X�̍\�z�v�i�ۑ�ԍ��F22500231�C��\�ҁF���c�R�����j�y�сC����24�N�x�C�w�K�@�헪�g�\�Z�ɂ�鎖�ƌv��uWEB ��̌o�ϊw�� e-Learning �V�X�e���iWeb:VisualEcoMath�j�̍\�z�v�ɂ��x������܂����B�����ɋL���Ďӈӂ�\���܂��B
�Q�l����
�m�P�n ���c�R�����Cand ���{���q�C�g�o�c���w����@�̂��߂̉�㈐��_�x�����ލ쐬�c�[��,�h �{�K�@��{�S�Z�_�W�Cvol. 48�Cno. 4�Cpp. 303-311�C2011.
�m�Q�n �Đ��T��C�A�u�_�N�V���� �����Ɣ����̘_���F�������[�C2007.
�m�R�n �Đ��T��C�p�[�X�̋L���w�F�������[�C1981.
�m�S�n �R�����j�C�_���I�ɍl���邱���F��g���X�C1985.
�m�T�n G. Pólya, How to Solve It: A New Aspect of Mathematical Method Princeton Science Library�C 2004.
�m�U�n M. J. Strauss, G. L. Bradley, and K. J. Smith, Calculus, 3rd ed., New Jersey: Prentice-Hall, Inc., 2002.
�m�V�n A. H. Schoenfeld, �gPolya, Problem Solving, and Education,�h Mathematics Magazine, vol. 60, no. 5, pp. 290, 1987.
�m�W�n ���q����C�،��A�i���X�g�̂��߂̐��w�ē����F�Ƃ��푍���T�[�r�X�C2004.
�m�X�n ���c�ꐳ�Cand �{����Z�C�g2.3 ��㈃f�[�^�x�[�X,�h �V�f�[�^�x�[�X�_ �W���牉㈁E�I�u�W�F�N�g�w�����C�v�Z�@�Ȋw�E�\�t�g�E�F�A�Z�p�u�� �S�C����: �����o�ŁC1994.
�m10�n G. Pólya, Mathematics and Plausible Reasoning, Vol 1. Induction and Analogy in Mathematics: Princeton University Press, 1954.
�m11�n G. Pólya, Mathematics and Plausible Reasoning, Vol 2. Patterns of Plausible Inference, Revised version: Princeton University Press, 1969.
�m12�n ������_�C�g���H�n�w������ł̒m�����L�Ɍ�����ICT ����V�X�e�� �i���W�����f�B�A�������ICT�j�C�h���f�B�A���猤���Cvol. 5�Cno. 1�Cpp. 27-34�C2008�C2008.
�m13�n ���c�R�����C�g�o�ύœK�������Ƃ��鐔�wWeb ���ގ����쐬�V�X�e���C�h �w�K�@��w�o�Ϙ_�W�Cvol. 41�Cno. 1�Cpp. 1-15�C2004.
�m14�n �X�c�T��Cand V. K. Billy�C�gWeb �x�[�XPSI �R�[�X�ɂ�����w�K�ߒ��Ɗw�K�X�^�C���Ƃ̊֘A���Ɋւ���ꕪ�� �i�R�~���j�P�[�V�������d������������H�Ə��������j�C�h ���{����H�w����W�Cvol. 6�Cno. 6�Cpp. 77-80�C2006�^12�^16�C2006.
�m15�n �쐼���C�V���m��Cand ���쎡�q�C�ge-Learning �����p�������w�O����Ɋւ�����،����i���W�����f�B�A�������ICT�j�C�h ���f�B�A���猤���Cvol. 5�Cno. 1�Cpp. 87-95�C2008, 2008.