【251 頁】

 

ブラック＝ショールズ方程式に関するシミュレーションとグラフィクスによる考察

 

白田　由香利＊

 

 

要約

 

学生にとって難解と思われているブラック＝ショールズ方程式であるが，視覚的にグラフィクス表現することで，理解が容易になる。本稿では，その確率的ブラウン運動を含む確率微分方程式に関するシミュレーション実験結果と代数学的に求められる理論的結果を３次元グラフィクスにより示す。確率的現象をコンピュータ上で再現することで，確率的ブラウン運動の理解が容易になり，同時に理論的に求められる正規分布を示し両者を比較することで，理論的事柄の理解を深める。また，オプションの期待値の導出過程における，期待値計算の積分計算範囲を，正規分布に従う確率変数と対数正規分布に従う確率変数に関して，両者同時にグラフィクスで視覚的に示す。本稿のグラフィクスの特長は，変数間の関係をスライダー操作によるモーションとして表現した点である。スライダーで変数を動かすことにより，複雑な関係式における他の変数への影響の理解が容易になる。

 

１．始めに

 

数理ファイナンスにおいて，ヨーロピアン・コール（及びプット）オプションの価格を求めるため，広くブラック＝ショールズ方程式が使われている［1，2］。ブラック＝ショールズ方程式では，そのボラティリティは定数としている。最近のボラティリティのモデルとしては，Dupire のローカルボラティリティモデル（時間と株価に依存）のような拡張モデルが使われるが，こうした拡張モデルを理解するためにも，ブラック＝ショールズ方程式のオプション期待値を導出する過程を理解することは重要である。また経済物理学における，べき分布を理解するためにも，まずは基本となる正規分布の確率密度に関する理解が重要である。本稿では，ブラック＝ショールズ方程式を深く理解するため，そのシミュレーションとグラフィクスによる導出過程の考察を行う。
　ブラック＝ショールズ方程式の株価期待値導出のための数学的ポイントは，以下の２点である。

【252 頁】

（１）ブラウン運動W（t）の確率過程を含む積分の近似式が特殊であること（伊藤のレンマ）。
理由は，Δw の二乗が，極限において，Δt に収束するからである。その結果，株価Sに対して，その利回りを，dS＝Sμdt＋SσdW（μはドリフト係数，σはボラティリティ）とモデル化すると，S=S0・eUとなるが，ここで確率変数U は正規分布
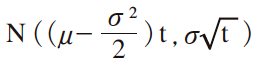に従う確率変数となる。

（２）株価S の確率分布をU の確率分布に置き直して，S の期待値を計算すること。

株価利回りS/S0の対数正規分布 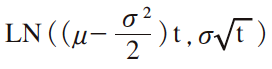を，自然対数をとった確率変数U, U＝Log（S/S0）に置き直して，その確率分布，正規分布 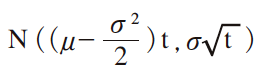を使い，U について積分し，オプション期待値を求めること。

 

この２つのポイントを理解するには，（１）についてはブラウン運動のシミュレーション，（２）については，確率分布のグラフィクスを用いた解説が有効である。本稿では，シミュレーションとグラフィクスを用いて，ブラック＝ショールズ方程式の導出過程を視覚化し，考察する。本稿では，数学ソフトMathematica を用いて，シミュレーション及びグラフィクス描画を行った。Mathematica は金融工学の分野において，オプション計算ツールとして広く普及しており，テキストも存在する［3−6］。しかし，これらのグラフィクスは２次元であり，多変数間の関係がグラフィクスで十分に表現されていない。そこで，本稿では，グラフィクスに，（１）３次元表示，および（２）スライダーによる対話的操作性を付加した。これにより，従来のオプション解説の図には無い，理解しやすい視覚化を行っている。
　本稿で用いる記号と変数名をまとめて記す：

・平均μ，標準偏差σの正規分布　N（μ, σ）

・確率変数X の期待値　E（X）

・標準ブラウン運動　W（t）〜N（0, 1）

・株価 （S0は初期値，μドリフト係数，σボラティリティ）

・株価の方程式　

 

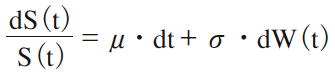
次節では，ブラウン運動による株価のシミュレーション，第３節では，グラフィクスによるオプション期待値導出を記述する。第４節はまとめである。

 

２．ブラウン運動による株価のシミュレーション

 

本節では，ブラウン運動W（t）および，以下の株価方程式のシミュレーション実験を行い，その理論的なモデルと比較し，合致することを確認する。

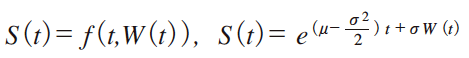
S（t）に対して，以下の確率積分が成り立つ［1］。これが伊藤のレンマである。式中，x＝W（t） 【253 頁】 としている。

 

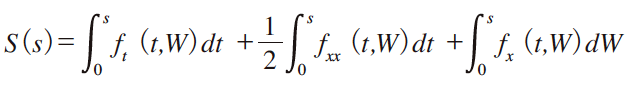
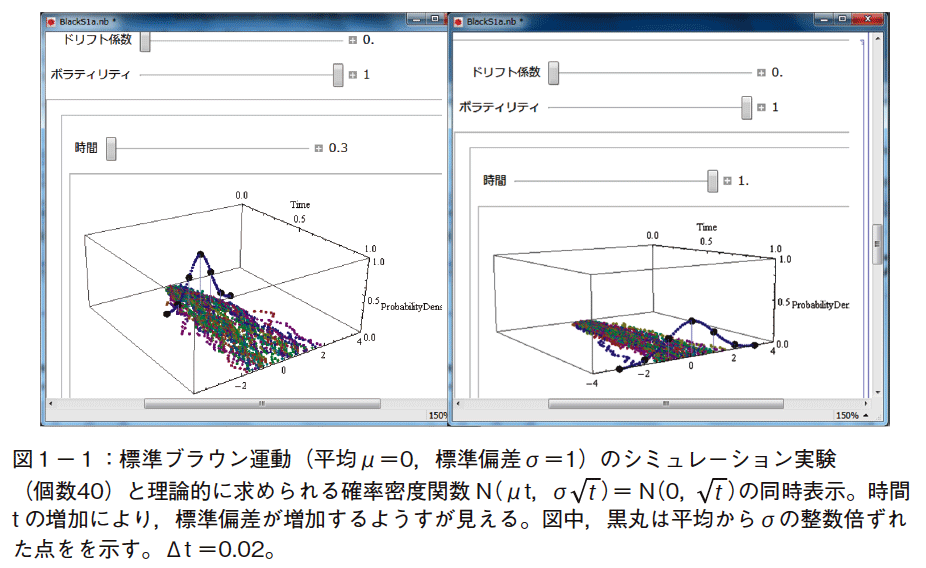
まず，標準ブラウン運動W（t）のシミュレーション実験と，W（t）の確率密度関数のグラフィクスを図１−１に示す。その右側の図が示すように，時刻 t をスライダーによって動かすことで，標準ブラウン運動の標準偏差が倍に増加するようすが分かる。確率密度関数における７個の黒丸は，W（t）の平均および平均からσの整数倍ずれた点を示す。±σの範囲に収まる確率は，理論的に約68％であるが，この図だけからでは判別できない。これに関しては図２でシミュレーション結果とその正規分布との比較を行う。
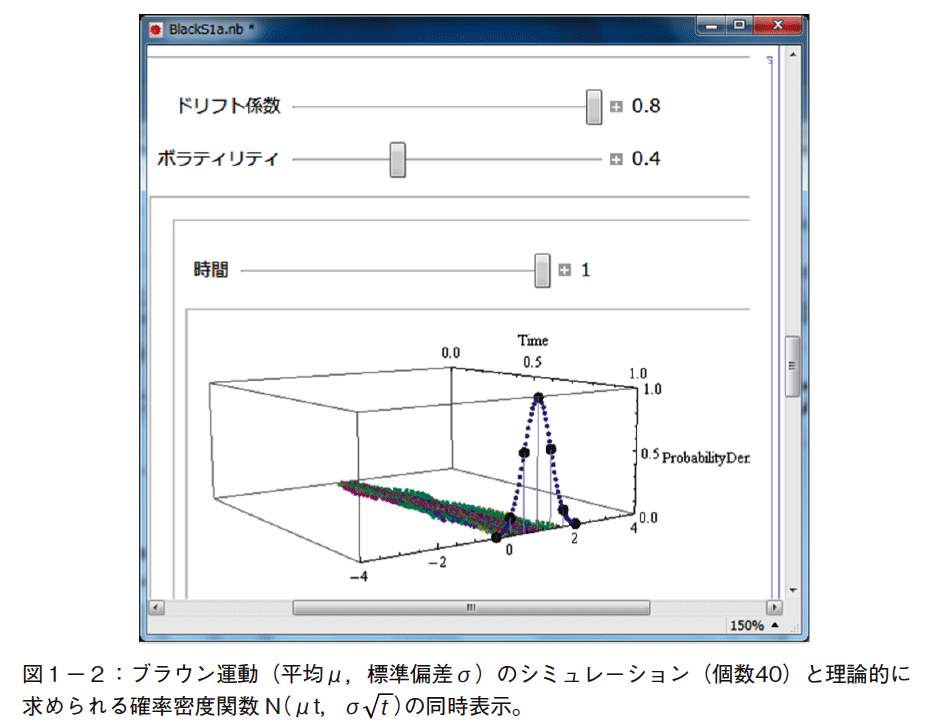
　また，図１−２では，一般のブラウン運動（平均μ，標準偏差σ）のシミュレーション（個数40）と理論的に求められるその確率密度関数N（μt, σ）を同時に表示した。スライダーによりドリフト係数を増加することで，時間に沿って，ブラウン運動W（t）の変化分の総和がずれていくようすが見える。
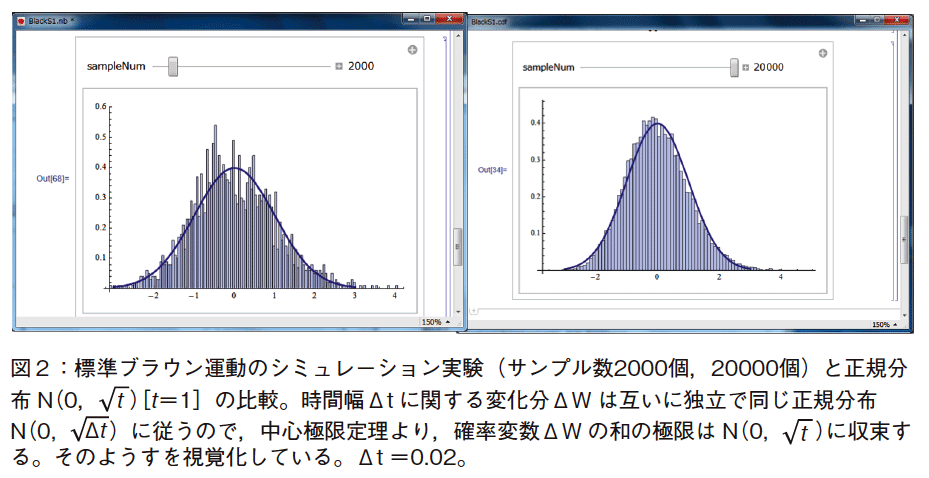
　図２には，シミュレーションの試行数を増加することで，正規分布に収束していくようすを示した。試行回数がスライダーによって増加させることができる。図１−１に比較して，確率密度関数が正規分布になることが，より明らかに見える。
　図３は，標準ブラウン運動の変化幅を平方した和（２次変分）のシミュレーション実験の結果を示す。標準ブラウン運動において，時間区分を細かくすると（分割数を増加させると），時間 t に収束するようすを示した。この図では，時間 t＝1を200分割している。スライダーにより時間区分を細分することで（dW）の二乗（２次変分）がdt に収束する，ことの数学的証明は複雑であるが，その意味を理解することは，このシミュレーション結果のグラフィクスに

 

 

【254 頁】

 

 

【255 頁】

 

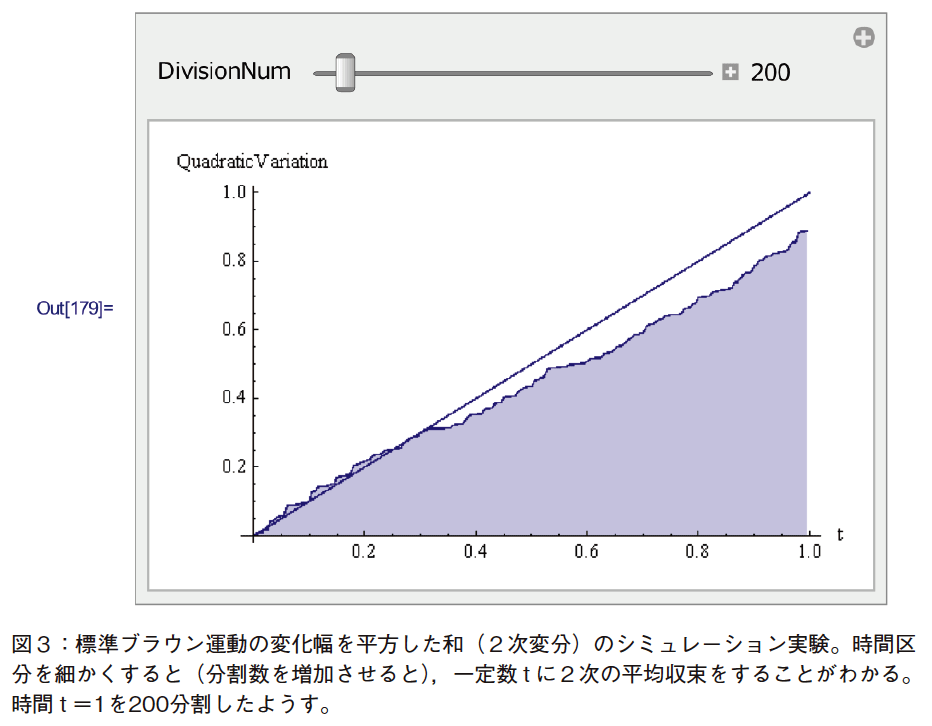
より可能であろう。

 

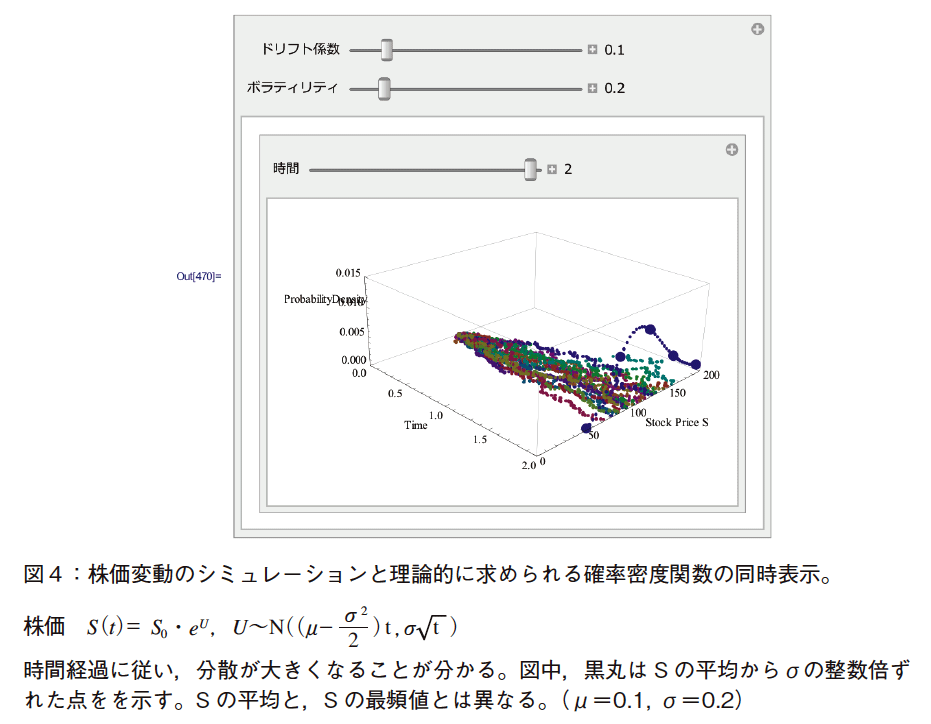
次に標準ブラウン運動W（t）を用いて，以下の株価の方程式をたて，シミュレーションにより，株価変動のようすを見る（図４参照）。t＝2，Δt＝0.01。

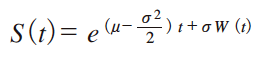
株価を確率変数U を用いて表すと，確率変数U の確率密度関数は以下のような正規分布をとなる。

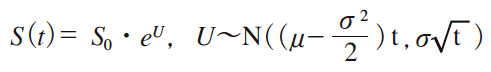
株価S は対数正規分布に従う。その確率密度関数は以下の式となる。

 

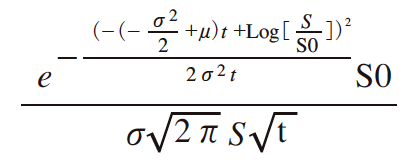
【256 頁】

 

 

【257 頁】

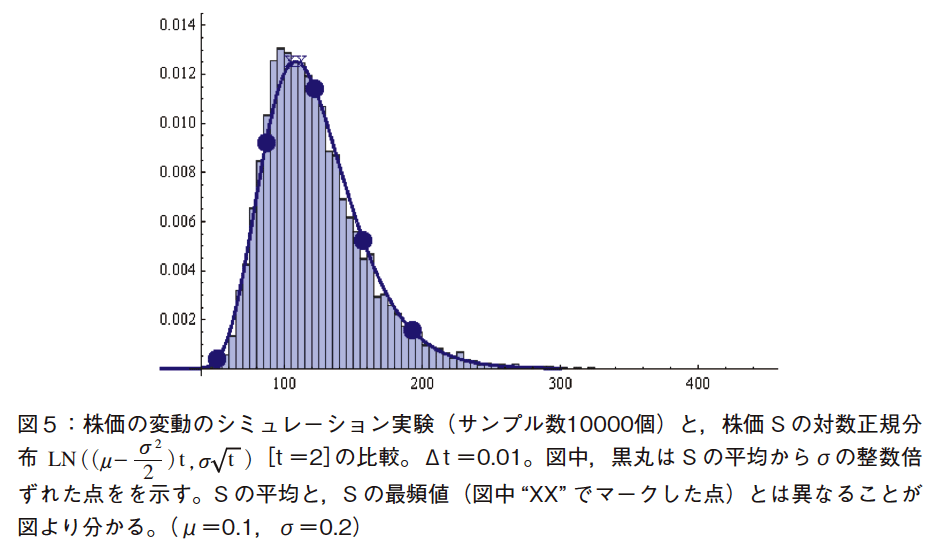
対数正規分布LN（μ, σ）は，正規分布と異なり，μおよびσは，その平均および標準偏差に対応しない。図５において，黒丸はS の平均からσの整数倍ずれた点を示す。ここでは，±2σの黒丸を描いている。対数正規分布では，理論的に，その平均と，その最頻値（確率密度が最大をとる値）は異なるが，図４，５からも，S の期待値は，最頻値からずれていることが分かる。対数正規分布LN（μ, σ）において，期待値は 最頻値は である［7］。

 

３．グラフィクスによるオプション期待値導出

 

本節では，コール・オプションの期待値導出をグラフィクスによって行う。
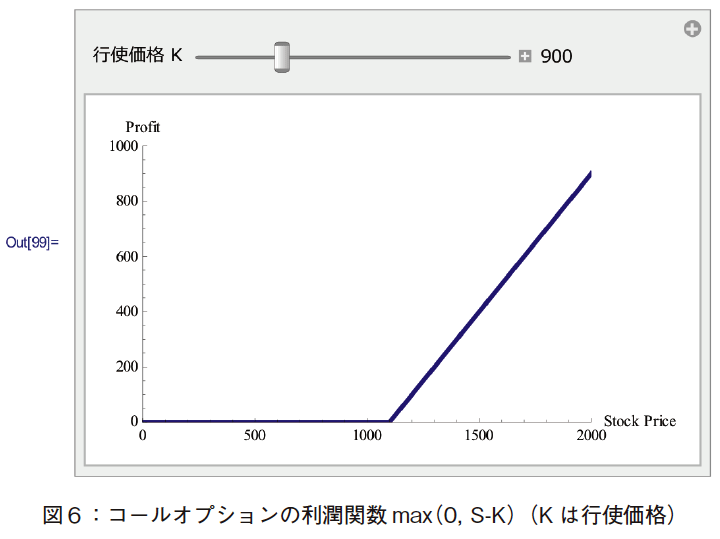
　コール・オプションの利潤は，図６のような増加関数となる。max（0, S−K）とは，S−K<0つまり，株価S が行使価格K 未満の場合，0となる。S−K>0となると，値は（S−K）となり，S の増加につれて，増加する。スライダーによりK を変化させると，利潤が０から正に転じる点が移動するようすがよく分かる。
　変数S の確率分布は，対数正規分布となる。対数正規分布とは，正規分布に従う確率変数UについてS=S0・eU の確率分布である。満期 t ＝ T における式を以下に示す。

 

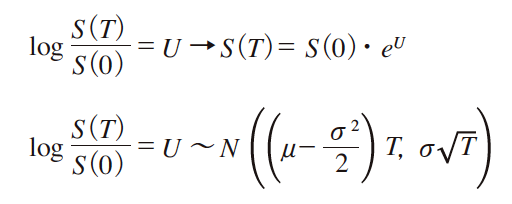
コール・オプション価格の期待値は，以下のように，S-K の期待値を求めればよい。換言すると，S-K を確率密度関数にかけてS についてS ≧ K の範囲で積分すれば求められる。

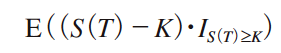
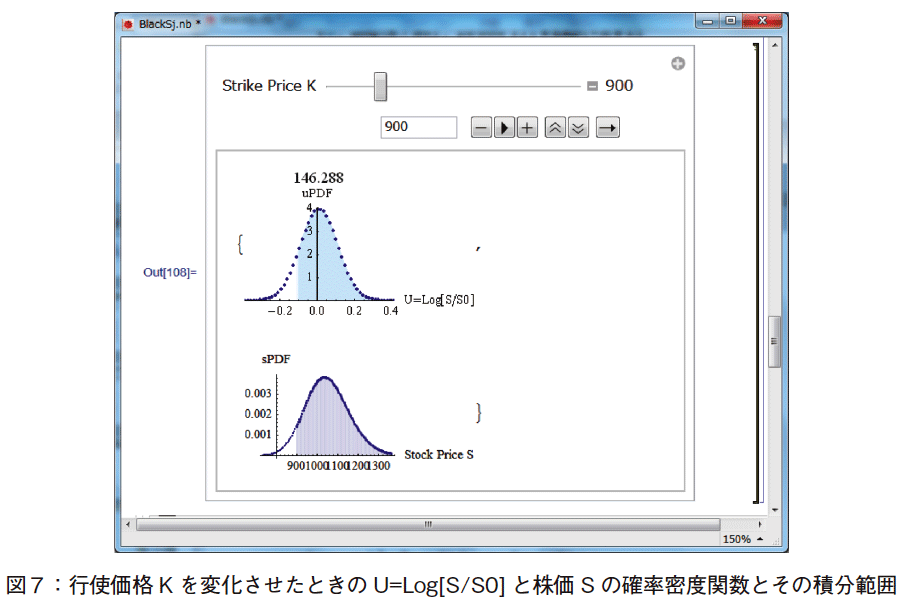
図７に，U とS の確率密度関数を示した。両者の積分範囲は其々，U ≧ ln（S/S0），S ≧ K となる。期待値を求めるため，その範囲で積分すると，オプションの期待値が求められる。求めたオプション期待値は，時刻 t における期待値である。最後に，現在価値PV に直すため，e −μt 倍することで，オプションの期待値の現在価値が求められる。
　確率変数S とU の間の関係式により，積分範囲が異なってくる，ということを理解するためには，図７にあるような，K を増減させるスライダーが有用と考える。スライダーを動かすことで，積分範囲（斜線の部分）の変動するようすがよく分かる。図７の図中，U の確率密度のグラフィクスの上にある数値（例：146.288）は，オプションの期待値の現在価値を示している。この計算は以下のブラック＝ショールズの公式を用いて行った。

 

【258 頁】

ブラック＝ショールズによるコール・オプションの価格公式［2］
コール・オプション価格 = S（0） ・ Φ（d1）−e −μt・ K・ Φ（d2）

 

Φ（d ）はN（0, 1）の−∞からd までの確率

 

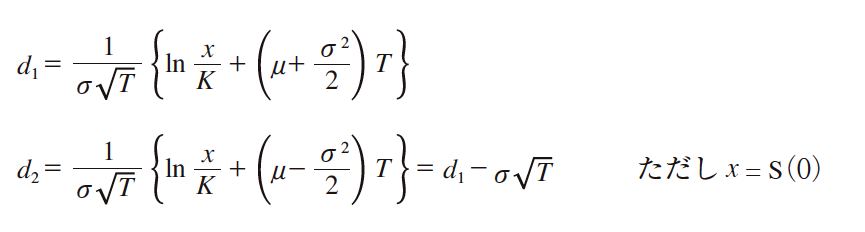
この公式が，（S−K）の期待値を，２項に分けて（S と−K）計算するため，その数学的意味が分からなくなってしまう学生もいるが，図６のようにオプションの利潤を見せながら，U による積分で求めていることを図７のように示せば，理解が容易になる。K をスライダーで動かすことで，積分範囲への影響をモーションとして見ることに効果があると考える。

 

 

【259 頁】

 

 

４．まとめ

 

本稿では，ブラック＝ショールズ方程式に関するシミュレーション実験と理論値のグラフィクスによる同時表示を行うことで，オプションの期待値を求める過程を分かり易く視覚化した。ブラウン運動に関する数式を理解するためには，ブラウン運動をシミュレーションして，見ることが効果的であると考える。ブラウン運動W（t）を含む積分の近似式が特殊であること（伊藤のレンマ）を分かり易くするため，標準ブラウン運動および，株価変動のシミュレーション実験を行い，その結果を，スライダーによって変数を変動させることにより，理論式の意味するところを視覚化するようにした。
　ブラック＝ショールズ方程式の株価期待値導出のためのもうひとつの数学的ポイントは，株価S の確率分布をU の確率分布に置き直して，S の期待値を計算すること，である。この理解のためには，スライダーで行使価格K を動かし，U とS の確率密度関数上で，S ≦ K の積分範囲を示すことが効果的と考えた。数理ファイナンスの分野では，対数正規分布の重要性が増しているが，正規分布に比較して，理解が容易ではない。しかし，その確率密度関数は既によく分析されている関数なので，それを直裁に視覚化したほうが，理解が容易になる，と考えた。
　本稿で述べたすべてのグラフィクスには，スライダーが付いている。それはスライダー操作により変数変動の影響をモーションとして可視化することが，その背後にある数学的性質の理解を容易にすると考えたからである。しかしながら，こうした負荷のかかる処理をスライダーで行うと，処理時間がかかり，数年前では実行不可能であった。現在は，この程度の負荷のシミュレーション実験であれば，特殊な高速CPU を用いずとも，ほとんど待ち時間なく，処理 【260 頁】 可能となった。本稿では，ブラック＝ショールズによるコール・オプションの価格公式を可視化した。今後とも，スライダー付の３次元グラフィクスによって，難解と考えられている数学プロセスを，可視化していきたい。

 

謝辞

本研究の一部は，平成24年度，科研費基礎研究（C）一般「推論エンジン法による知識ベースの構築」（課題番号：22500231，代表者：白田由香利）及び，平成24年度，学習院戦略枠予算による事業計画「WEB 上の経済学部e-Learning システム（Web: HowToSolveIt）の構築」により支援されました。ここに記して謝意を表します。

 

参考文献

［１］ 松原望，入門確率過程：東京図書，2003。

 

［２］ 松原望，松原望の確率過程超！入門：東京図書，2011。

 

［３］ M. A. H. Dempster, Mathematics of derivative securities : Cambridge Univ. Press，1998.

 

［４］ 大川勉，金融工学入門。京都：阿吽社，2002。

 

［５］ 椎原浩輔，Mathematica による金融工学：東京電機大学出版局，2000。

 

［６］ S. Stojanovic, Computational financial mathematics using Mathematica: optimal trading in stocks and options Boston: Birkhäuser 2003.

 

［７］ 蓑谷千凰彦，入門確率過程：朝倉書店，2003。