【31 頁】
固有値の概念の教授法
─経営学科に適した線型代数の教授法─
白田 由香利1)
要旨
本稿では,経営学科の学生に固有値の概念を理解させる教授法として,対角行列で表わされる線型変換を初めに与える方法を提案する。そこでは,始めに,固有値とはその拡大操作による各軸方向の拡大率である,という比喩を用いて説明する。ついで,この拡大操作を複数の非直交座標系に対して行う際,基底変換が必要である,と説明する。伝えるべきことは,直感的解釈として,この対角行列で表される拡大マシンの,各軸方向への倍率が固有値であり,2次元の場合,拡大操作行列の2つの列ベクトルの作る面積が行列式であり,その両者の値は基底を変えても不変,ということである。この教授法を使って,主成分分析を比喩的に説明した。主成分分析とは,その分散共分散行列の固有値を求め,固有値を固有ベクトル方向のデータの分散の度合いと解釈する分析法である。固有ベクトル方向に拡大した様子を分析することが,主成分分析の目的である,と説明する。
1.始めに
経営学科では,データ分析において多変量解析を多用する。その中で,分散共分散行列および固有値は頻出する重要概念である。その数学的意味を理解すれば,多変量解析全般の理解が体系的に行えて,分析がクリアに行えると筆者は考える。しかしながら,現場の演習を見ていると,多変量解析の理論にはあまり触れず,学生は解析ソフトウェアのコンピュータ出力をいかに判読するかにのみ注力しているように見受けられる。殆どの学生は,「固有値が基底によらない不変量である」ということには全く興味を示さず,その数学的重要性に気づいていない。
固有値の概念を理解すると,経営学において多変量解析および最適化問題を扱う場合,その数学的過程を体系的に考えられるようになる。そのために,経営学科の学生に対して,どのように固有値の概念を説明するか,教授法が重要となる。
そこで現在行われている,固有値の教授法を考えてみる。線型代数のテキストでは,どのように固有値を教えているか,サーベイしてみると,以下のような順序で行われているものが殆どである[1−4]:まず,ある行列が与えられて,それの固有値を計算してみる。そして,其々
【32
頁】
の固有値についてその固有ベクトルを求める。その固有ベクトルを使って対角化を行う,という流れである。
この流れは,筆者が大学1年のとき,理学部の線型代数の講義で教えて頂いたときと全く同じである。英語の線型代数のテキストを見ても,多くがこの流れで書いている。重要な概念は,「基底ベクトルは変化しても,固有値および行列式の値は不変」ということだが,殆どのテキストは,あっさりとそれを記しているだけである。簡単に触れられるだけで,学生が理解できるとは考えにくい。その不親切にも思える記述のシンプルさの理由として,「それは各人が自分で体得するもので,過剰に説明しようとすると,数学的でない表現になりがちで,それを避けるために,シンプルでクリアな数学的な表現にとどまる」からだと考えられる。
筆者は数学科の学生にヒアリングを行い,彼らが「固有値が不変量である」ということを理解していることをまず確認し,どのように理解したかを質問してみた。数学科の場合,各種の講義で何度も繰り返し固有値について学ぶ機会があるので,自分なりに固有値の本質を理解していくと推測される。数学科では数学的に厳密な表現しか使わないが,繰り返し説明されること,また,彼らが元々抽象的な数学を志す学生であるので,自分で体得できるものと推測される。しかし,数学科ではない,応用として線型代数を使う経営学科では,どのように固有値の概念を教育すべきか,それが本稿の主題である。筆者の考えでは,広く経営学科の学生に線型代数を理解してもらうためには,抽象数学を学ぶ数学科学生のためのテキストとは異なる,経営学科のための線型代数のテキストというものが存在するべきではないか,と考える。
雄弁に固有値の概念を伝えようとしているテキストもある。野崎は,「どこかにベクトル空間と線形写像という真の存在があり,行列やベクトルの見た目(成分表示)は,世を忍ぶ仮の姿であって,基底のとり方によってさまざまに変わる。(途中略す)実は固有値というのは,真の存在の持っている不変な情報なので,基底をさまざまに取り替えて,行列表示の見た目が変わっても,固有値自体は変わらない」という表現によって固有値の概念を説明しようとしている[5]。
石井は「旧番地の移動情報を新番地で言い換えるには−基底の取替えと線型変換」という比喩を用いて説明している[6]。また,多変量解析と固有ベクトルとの関連を説明するコラムとして,主成分分析を取り上げている[6]。こうした比喩は,数学に苦手意識をもつ学生の助けになると考える。
また,吉田は,雑誌「理系への数学」の連載記事「2次元で学ぶ 大学への線形代数入門」において,理系を対象として,線形代数に嫌悪感を抱かせないように表現しながら,線形代数の一般理論のイメージを説明している[7]。この記事は,抽象数学に進む人と,応用的に数学を使う人の両方に役立つように書かれている。
筆者は,本稿において,経営学科のための固有値の説明方法を提案する。それは「固有値は拡大マシンの倍率である」という説明である。そのための寓話を日本語と英語で書いた。これは筆者のWEB ページから参照可能となっている[8]。以下の章では,第2節で,この寓話のエッセンスを述べる。第3節では,この考え方をベースに,経営学でよく使われる多変量分析である主成分分析における,固有値の意味を考える。最後はまとめである。
【33 頁】
2.固有値の概念の教授法
本節では,筆者が提案する固有値の概念の説明方法を述べる。殆どの線型代数のテキストでは,何かある行列が与えられて,その固有値を計算する,という始まりかたをする。これに対し,筆者の提案する説明法では,始めに,拡大操作のための対角行列(対角成分以外の成分が0である行列)を提示することがポイントである。
基底であるが,始めの拠り所として正規直交基底を考える。正規直交基底ベクトルは,互いに垂直で,各々の大きさは1である。そして,別の基底として,非直交基底ベクトルを考える。始めの拠り所として正規直交基底を考える理由は,初めから本質的な抽象的存在である線型変換Tを考えることは難しいからである。抽象概念である線型変換Tを,具体的な行列として表すのであれば,それは非直交基底よりも直交基底であるほうが,始めの拠り所として適している。
以下の説明では,簡単のため,行列の次数は2とする。しかし,以下の内容は一般の次数n(nは自然数)に拡張可能である。以下の,説明順序のための,ステップを示す。
(1) 2つの基底を提示する。
始めの拠り所となる基底は正規直交基底とする。もう一方の基底は,非直交基底とする。学生には,ある点に関する,両者の基底間の座標変換の演習を行わせることで,座標は基底に依存することを理解させる。
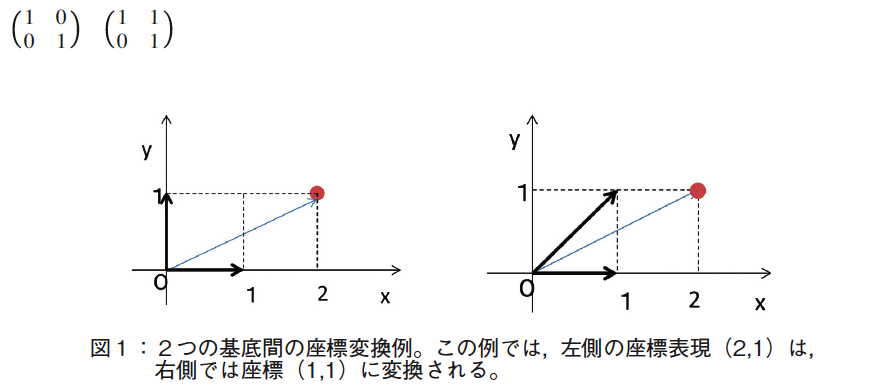
例えば,2つの基底を以下のように取る。すると,図1に示すような座標変換例を示す。
(2) その正規直交基底のもと,対角行列で表現される拡大操作MAGNI を定義する。
例えば,対応する直交空間においてx方向に3倍,y方向に2倍する拡大操作 MAGNI を考える。そのとき,対応する行列は以下のようになる。
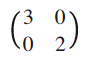
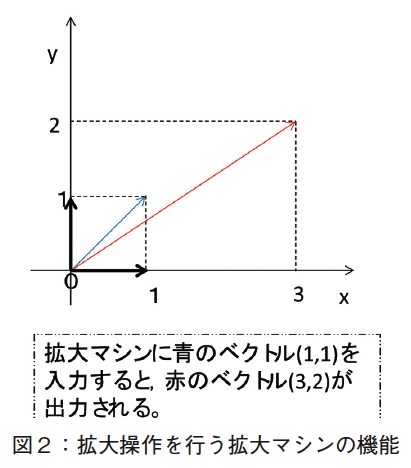
この行列をベクトルに作用されることを拡大マシンと解釈すると,例えば,青のベクトル 【34 頁】 (1, 1)を入力すると,赤のベクトル(3, 2)が出力される(図2参照)。
この場合,その対角行列の対角要素が固有値である。
固有ベクトル 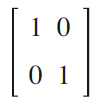 ,固有値 3, 2
,固有値 3, 2
学生は,こうした各軸方向への定数倍の拡大,という操作に対する行列表現は容易に理解する。筆者は講義では,「直交空間の世界で,大きさを拡大するマシンを発明したので,それを,他の非直交空間の世界に輸出することを考えましょう。しかし,マシンは直交空間のこの座標系でしか動かないようになっているので,翻訳機能が必要です」という比喩を使って説明している。演習においては,非対角行列による線型変換では,回転とスキューなどが起こってしまい,各軸方向への定数倍の拡大にはならないことを確認させる。
(3) この拡大操作を,非直交座標系で表現すると,どのような行列になるかを考える。
非直交系座標を w とする。直交系座標を c とする。その場合,以下のような線型変換の組合せで,求めたい行列が得られる。
(入力:座標表現w)
↓
P −1 座標表現wからcへの変換
↓
A 拡大変換
↓
P 座標表現cからwへの変換
↓
(出力:座標表現w)
【35 頁】
例えば,非直交空間のベクトルを以下のようにとる。
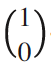 ,
,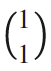
座標変換の行列を考えると,基底ベクトルがそれぞれ,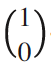 が
が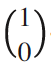 に移り,
に移り,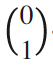 が
が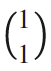 に移るため,座標表現cからwへの変換行列P は
に移るため,座標表現cからwへの変換行列P は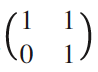 となる。
となる。
この座標変換行列をP としたならば,P には逆行列P −1が存在する。計算すると以下のようになる。
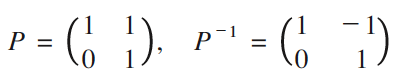
拡大のための行列が,A=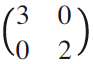 であった。この行列A に座標変換を施した,座標wに対する拡大操作行列は,行列B = P A P −1と定義される。筆者は,これを比喩的に「翻訳機能つき,拡大マシンの行列表現」と説明している。この例では,行列B は以下の通り。
であった。この行列A に座標変換を施した,座標wに対する拡大操作行列は,行列B = P A P −1と定義される。筆者は,これを比喩的に「翻訳機能つき,拡大マシンの行列表現」と説明している。この例では,行列B は以下の通り。
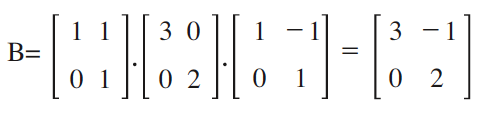
(4) この行列B の固有値が,行列MAGNI の固有値と等しいことを確認する。また,行列Bの固有ベクトルが,この非直交空間の基底ベクトルに等しいことを確認する。
特性方程式を使って計算すると,以下のようになる。固有値が3,2で,行列MAGNI の固有値と等しいことが確認できる。また,行列B の固有ベクトルが,始めに設定した,非直交空間の固有ベクトルに等しいことも確認できる。2つの基底ベクトルの位置関係によって,負の値の場合もあります。
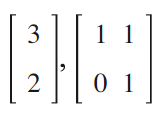
(5) 次に,行列の行列式が,2次元空間では,その2つの列ベクトルの作る面積であること,行列式の値は,基底変換に関して不変であることを確認する。
これは,以下のように説明する:「行列MAGNI の行列式の値は6です。基底変換後の行列B の行列式の値も6です。基底変換を行っても拡大操作の行列の固有値,行列式の値は不変です。これは図形的に見ると,その拡大操作行列の列ベクトルの作る面積(0及び負もある)となります。」
【36 頁】
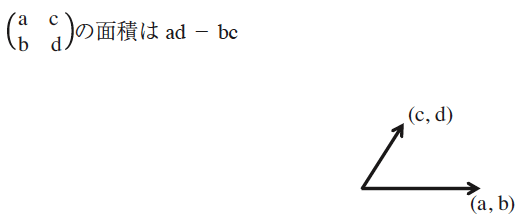
(6) 別の非直交空間に対して,上記(3)〜(5)と同じ操作を行う。これにより,基底ベクトルを変えても,行列MAGNI の固有値と固有値が同じになること,行列式の値は同じになること,を確認させる。
これを複数の非直交座標系に対して行う際,筆者は「各種の異なる基底ベクトルをもつ国に,この拡大マシンを輸出することを考えます。その国にあった,翻訳機能をつけましょう」という比喩を使って説明している。学生は次のように理解するであろう:拡大マシンが始めに定義された時の各成分の倍率が固有値であり,その拡大操作の行列の列ベクトルの作る面積が行列式で,その両者の値は基底ベクトルを変えても不変,である。
このように教授した場合のデメリットは,本来,抽象的で座標系にはよらない線型変換に対して,直交空間における対角行列で表わされる線型変換という狭いイメージをもたせてしまうことである。つまり,何か直交する単位ベクトルを基底とする線型空間があり,そこでの拡大操作を基準に考える,というように,学生の線型変換に対するイメージをせばめてしまう。しかし,理解のしやすさから考えると,こちらのほうが格段に分りやすいと考える。また,経営学科における線型代数の教授法としては,入門的説明としては直感的なこの説明で十分である,と考える。
3.主成分分析における固有値の解釈
ここまで,固有値の概念の教授法を提案したが,この方法により固有値を理解した学生は,多変量解析における固有値の解釈も容易になるであろう。本節では,主成分分析の固有値の解釈に関して,比喩的な拡大マシンの拡大率の解釈を適応してみる。
主成分分析とはどのような分析であったか簡単にレビューする。まず,データの平均値を原点に移動する。これは平行移動は線型変換ではないからである。次に,分散が最大となるように主成分軸方向を決める。この分散最大化を視覚化して説明するために,筆者も後述するグラフィクスツールを作った。久保山は,直感的イメージをもたせるために,サカナ型のデータ群を,各種の方向から見て,主成分軸を探す,というイラストで分散最大化を説明している[9]。
主成分分析においては,分散共分散行列の固有値が主成分方向の分散の値となる。次数が2の場合,固有値は2個求まる。大きいほうの固有値が第1主成分の分散値であり,もうひとつの固有値が第2主成分の分散値である。2つの固有ベクトルは,それぞれ,主成分軸の方向を示している。分散共分散行列は対称行列であるので,固有ベクトルは直交する。つまり,第1主成分軸と第2主成分軸は直交する。また,この分散最大化問題を解くときに,制約条件として,固有ベクトルの大きさが1になる条件を入れているので,回転すれば,単位ベクトルとな
【37 頁】
る。
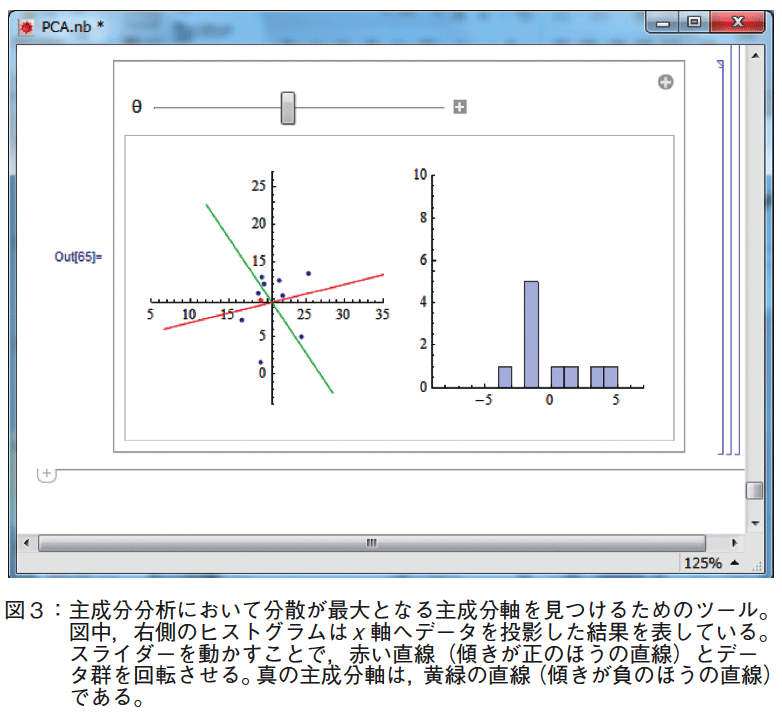
ここまでは,一般的な主成分分析の教授法である。以降では,拡大マシンの比喩を入れて説明をしていく。分散共分散行列の固有値は,基準の直交空間における拡大操作の拡大率に対応するが,その意味を考察していく。属性が2個の場合,ヒストグラムを描くと,図3のようになる。これは主成分分析において分散が最大となる主成分軸を見つけるためのツールである。図中,右側のヒストグラムは x 軸へデータを投影した結果を表している。スライダーを動かすことで,赤い直線及びデータ群を回転させる。それにより,ヒストグラム上で分散が最大となる軸の角度を発見していく。真の主成分軸は,黄緑の直線(傾きが負のほうの直線)で示してある。
主成分分析で主成分軸を見つけるということは,拡大マシンを定義した始めの直交空間の基底ベクトルの方向を見つけることである。その直交空間においては,第1主成分軸が1番目の基底ベクトル方向の軸に,第2主成分軸が2番目の基底ベクトル方向の軸に対応している。基底ベクトルは単位ベクトルである。拡大マシンの拡大比率は,各主成分軸方向へのデータの分散の度合いを表す。
つまり,主成分分析とは,与えられた分散共分散行列の固有値を発見することで,拡大マシンを定義した基準の直交空間の基底ベクトルを求め,その基底ベクトル方向に,データ集合をどの程度拡大(分散)させているかを求める分析手法である,と比喩的に説明できる。
【38 頁】
この説明を使うと,固有値の大きさが,基準となる直交空間におけるそのデータが元来もっている分散の度合いを表すことが直感的に理解できる。また,拡大マシンが各軸方向への定数倍の拡大比率をもっていたことから類推することで,属性間の依存性がない,互いに独立な新たな属性を定義していることが直感的に理解できる。
固有値の問題からいったん離れて,分散最大化の制約付き最適化問題として,この問題を扱ってみる。Var を分散を求める操作,Cov を共分散を求める操作と定義すると,この問題は主成分 z=ax+by に対して以下のVar(z)を最大とする a, b を求める制約付き問題と解釈できる。
Var(z)= Var(a・x+b・y)
= a2・Var(x)+b2・Var(y)+2a・b・Cov(x,y)
a2+b2 = 1
この制約付き最適化問題をラグランジェの未定乗数法を使って解くと,以下のような,特性方程式が出てくる。制約付き最適化問題として解いていると,それが分散共分散行列の固有値問題になる。そして,ラグランジェ乗数λが,実は,固有値であったことが分る。
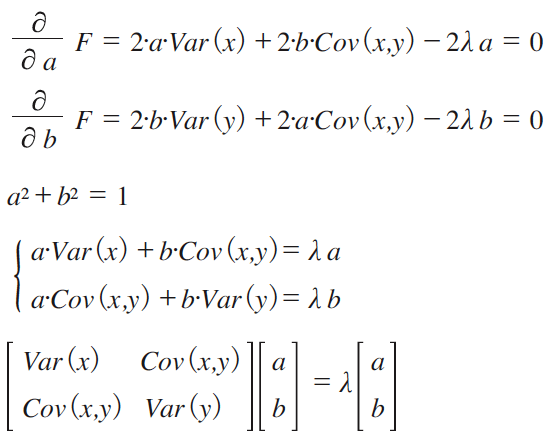
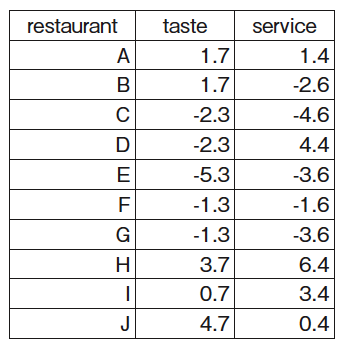
具体的な以下のようなデータを使って,主成分分析を行ってみる。この例では,レストランの評価属性として,味(taste)と,サービス(service)の2つをとっている。データは,既に平均値を0とするように平行移動してある。
【39 頁】
このデータの分散共分散行列は以下のような対称行列となる。
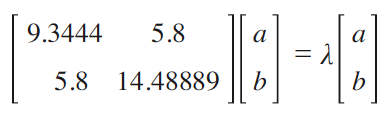
そして,その固有値および固有ベクトルを求める。

固有値は約18.3,5.6となる。又,その2つの固有ベクトルは,直交していることが分る。
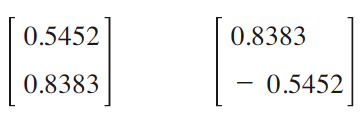
これをグラフィクスで表示すると以下のようになる(図4参照)。可動領域のカーブ(赤色)を見ると,その最大値が,大きいほうの固有値18.3,最小値が小さいほうの固有値 5.6に対応していることがグラフィクスから読み取れる。分散Var(z)の3次元グラフィクスを見ると,分散値は其々の主成分軸に関して線対称となるようすが分る。
【40 頁】
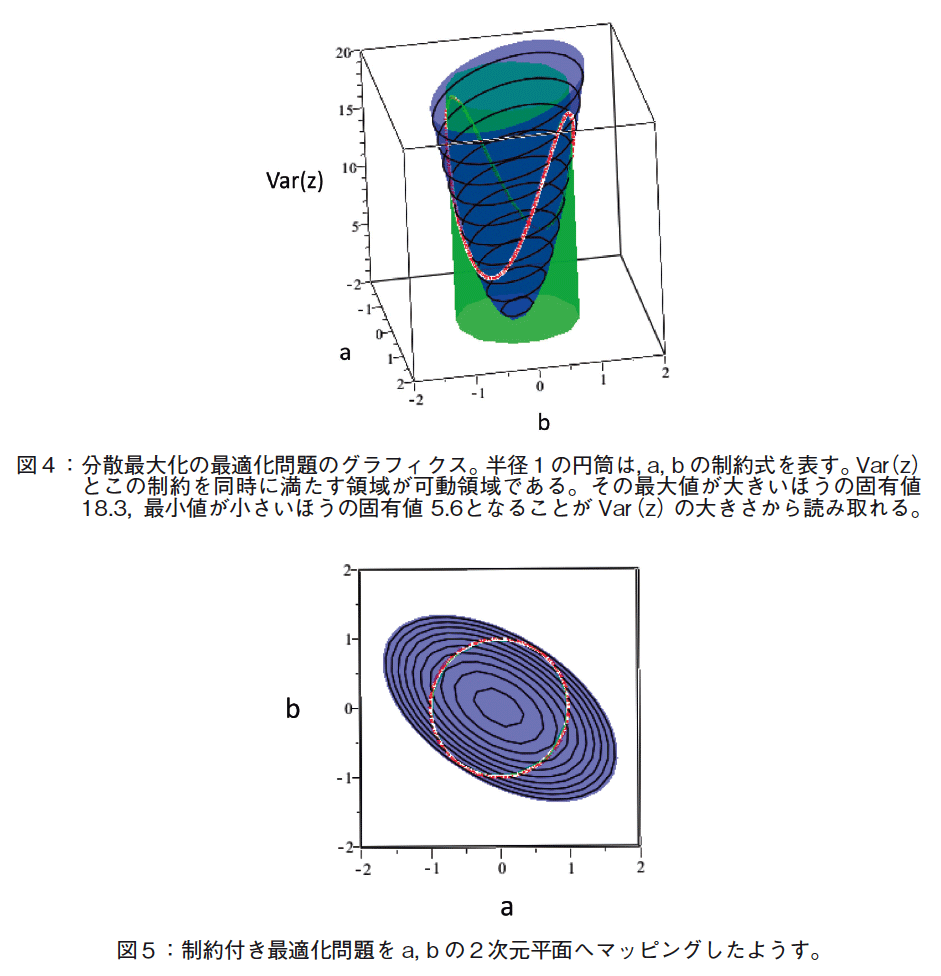
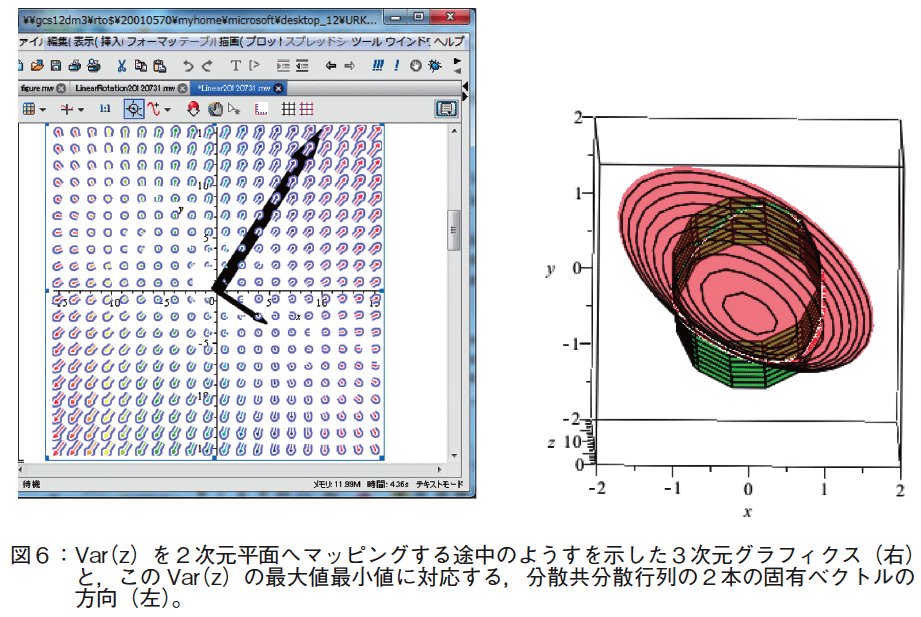
図4の3次元グラフィクスをa, b の2次元平面へマッピングしたようすを図5に示す。赤い円が制約式である。図6では,2次元平面へマッピングする途中の3次元グラフィクスと,2本の固有ベクトルの方向を示した。固有ベクトルは単位ベクトルであるが,グラフィクスでは固有値倍して長さで固有値の大きさを示すようにした。
【41 頁】
主成分分析で始めに与えられたデータの分散共分散行列は,対角化されていない対称行列である。主成分分析とは,その分散共分散行列の,真の拡大マシンとしての拡大率を求めようとしていると,比喩的に言える。始めに真の拡大マシンが定義された基底ベクトルを求めることで,主成分軸の方向が求められる。固有値は拡大マシンの主成分軸方向の拡大率と解釈できる。拡大率が大きいほど,その方向にデータが分散していると解釈できる。すなわち,固有値は与えられたデータ群の分散している程度を表すと言える。基底ベクトルを回転させて座標系を変えても,固有値の値(主成分の値)は不変である。
4.まとめ
本稿では,経営学科の学生に固有値の概念を理解させる教授法として,固有値は真の拡大マシンの軸方向の拡大率である,という比喩を用いた説明を提案した。ポイントは始めに,対角行列によって拡大マシンの拡大変換を提示することである。この拡大操作を複数の非直交座標系に対して行う際,「各種の異なる基底ベクトルをもつ国に,この拡大マシンを輸出することを考えます。その国にあった,翻訳機能をつけましょう」という比喩を使って基底変換を説明する。固有値の直感的解釈として,真の拡大マシンの基底ベクトル方向への倍率が固有値であり,拡大操作の行列の列ベクトルの作る面積が行列式で,その両者の値は基底を変えても不変,となる。
このように教授した場合のデメリットは,本来,抽象的で座標系にはよらない線型変換に対して,直交空間における対角行列で表わされるような線型変換という狭いイメージをもたせて
【42
頁】
しまうことである。つまり,何か直交する単位ベクトルを基底とする線型空間があり,そこでの拡大操作を基準に考える,というように,学生の線型変換に対するイメージをせばめてしまう。しかし,理解のしやすさから考えると,こちらのほうが格段に分りやすいと考える。また,経営学科における線型代数の導入的教授法としては,直感的なこの説明で十分である,と考える。
本稿の後半では,この教授法を使って,主成分分析を比喩的に説明した。主成分分析では始めにデータの分散共分散行列を計算する。主成分分析とは,その分散共分散行列の,真の拡大マシンとしての拡大率を求めようとしていると,比喩的に言える。始めに真の拡大マシンが定義された基底ベクトルを求めることで,主成分軸の方向が求められる。固有値は拡大マシンの主成分軸方向の拡大率と解釈できる。拡大率が大きいほど,その方向にデータが分散していると解釈できる。すなわち,固有値は与えられたデータ群の分散している程度を表すと言える。基底ベクトルを回転させて座標系を変えても,固有値の値は不変である。
経営におけるデータ分析では行列を多く使う。学生が真にデータ分析手法を理解するためには,ある程度の線型代数の知識は必要である。しかし数学科のように抽象的な概念として理解する必要はない。経営学科に適した行列に関する数学の教授法を今後とも考えていきたい。
謝辞
本研究の一部は,平成24年度,科研費基礎研究(C)一般「推論エンジン法による知識ベースの構築」(課題番号: 22500231,代表者:白田由香利)及び,平成24年度,学習院戦略枠予算による事業計画「WEB 上の経済学部 e-Learning システム(Web: HowToSolveIt)の構築」により支援されました。ここに記して謝意を表します。
参考文献
[1] Nicholson, W. K., Linear Algebra (Sixth edition), 2003: McGRAW-HILL International Edition.
[2] Lipschutz, S., Beginning Linear Algebra. SHCAUM’s outlines, 1997: McGRAW-HILL
[3]中井達,経済数学 線形代数編,2008: ミネルヴァ書房。
[4] Schott, J. R., 訳: 豊田秀樹,統計学のための線形代数, 2011:朝倉書店。
[5] 野崎亮太,図解でわかる線型代数,2004:日本実業出版社。
[6] 石井俊全,意味がわかる線形代数,ベレ出版,2011。
[7] 吉田信夫,2次元で学ぶ 大学への線形代数入門,理系への数学,2012年5月号〜2013年8月号, 現代数学社。
[8] Shirota, Y. and T. Hashimoto, Bond Mathematics by Graphics - graphics 10 -, 2011; Available from: http://www-cc. gakushuin. ac. jp/~20010570/private/MAXIMA/.
[9] 奥瀬喜之,久保山哲二,経済・経営・商学のための実践データ分析,2012:講談社。