�y43 �Łz
��㈐��_�@�ɂ��u���b�N���V���[���Y�������̓��o
���c�@�R����1�j
�v�|
�o�ϐ��w�����������߂ɂ́C�l�́C��㈁C�A�[�C�A�u�_�N�V�����Ȃǂ𑍍��I�ɋ�g���Đ��_���s���Ă���ƍl������B���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���ĉ����𗧂ĂĈ�����\�����Ȃ���C���͑�� Unknown ���� Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����C�M�҂͍l����B���̋t�������_�����̗L������]�����邽�߁C�{�e�ł́C����ƌ�����u���b�N���V���[���Y�������̓��o�͑�Ƃ��ĉ������Ƃ𐄘_�����ōs���Ă݂��B���ʂƂ��āC���̓��o�Ɋւ��ẮC���Ғl���犔���̊��`�����߂�C�����̊����炻�̊m�����x���`�����߂�C�Ƃ����Q�̑�̕����́C�t�������_���A�u�_�N�V�����Ƃ��čs���Ă���B�������C�����ڕW�̐��_�����ł́C�O�������_�������I�ɍs���Ă���B���������t�������_�����ŁC�u���b�N���V���[���Y�������̓��o��������ƁC���f���쐬�̑O������ɉ��^�I�ɂȂ�C�����̌��ƂȂ鉼�����炻�̉�����I���������R�𐄎@���邱�ƂŁC����ɐ[�����̌����𗝉��ł���悤�ɂȂ�B
�P�D�n�߂�
�o�ϐ��w�̏����������ꍇ�C���m�̌����y�уZ�I���[���ǂ̂悤�ɑg�ݍ��킹�āC���m�������߂邩�C�v���Z�X���d�v�ł���B�o�ϐ��w�����������߂ɂ́C�l�́C��㈁C�A�[�C�A�u�_�N�V�����Ȃǂ𑍍��I�ɋ�g���Đ��_���s���Ă���ƍl������B���̂悤�Ș_���I�Ȑ��_�\�͂��J�����邱�Ƃ����w����̑��ړI�ł���Ɖ�X�͍l���C��㈐��_�@�ɂ�鐔�w��������H���Ă����B�{���������X�L���́C�i�P�j�����������̑g�����ł����@�v���Z�X�𗝉����邱�Ɓi�����ʼn����Ȃ��Ă��C�������𗝉�����j�C�i�Q�j�Ɨ͂ł��̉�@�v���Z�X���v�����邱�ƁC�ł���B���̂Q��ނ̃X�L���{���̂��߁C��X�� web: VisualEconoMath �Ƃ����V�X�e�����J�����C���ۂ̌o�c���w�̍u�`�Ŋ��p���Ă���m�P�|�R�n�B
�@��̔��c�̘_���ɂ����ẮC�u���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���ĉ����𗧂ĂĈ�����\�����Ȃ���C���͑�� Unknown ���� Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����v�Ƙ_�����m�S�C�T�n�B���̋t�������_�����̗L������]�����邽�߁C�{�e�ł́C����ƌ�����u���b�N���V���[���Y�������̓��o
�y44
�Łz
�͑�Ƃ��ĉ������Ƃ𐄘_�����ōs���B���߂ł́C�u���b�N���V���[���Y�������̓��o�̂��߂̉�㈐��_�ł́C�t�������_���ǂ̂悤�ɍs���Ă��邩�C�����̎��v���̃��f�����̃A�C�f�A���܂߂āC�S�̂̍l�����̗����_����B��R�߂ł́C�u���b�N���V���[���Y���������o�ɂ́C�ǂ̂悤�Ȍ������m���Ƃ��ĕK�v�ł��邩�C��������ƁC�ǂ̌������������������_���āC�g�������ސ�������B��S�߂ł́C���̋t�������_�����ŋ��������ʂɂ��Ę_����B��T�߂͂܂Ƃ߂ł���B
�Q�D�t�������_
�{�߂ł́C�u���b�N���V���[���Y�������̓��o���C�t�������_�ɂ���čl����B�u���b�N���V���[���Y��������1973�N�Ƀt�B�b�V���[�E�u���b�N�iFischer Black�j�ƃ}�C�����E�V���[���Y�iMyron Scholes�j�������Ŕ��\�������_�ł���C���̌����������ɏؖ��������o�[�g�E�}�[�g���iRobert C. Merton�j�ƂƂ��ɂR�l��1997�N�Ƀm�[�x���o�ϊw�܂���܂����m�U�n�B�u���b�N���炪�������v�������ۂɁC�ǂ̂悤�Ȑ��_���s�������̎��ۂ͕s���ł���B�ȍ~�ł́C���҂̏���Ȑ��@�ŁC���̐��_�ߒ��𐄎@���Ă����B
�@�u���b�N���V���[���Y�������Ƃ́C�R�[���I�v�V�����ƌĂ����Z���i�̊��Ғl�����߂�����ł���B�{�e�ł́C���[���s�A���E�R�[���I�v�V�����݂̂�ΏۂƂ���B���̎�ނ̃v�b�g�I�v�V�����Ȃǂ́C���̃I�v�V�����̌����𗝉�����C�ގ��̍l�����ʼn������Ƃ��\�ł���B�e��̃I�v�V�����̐����y�сC�u���b�N���V���[���Y�������̓��o�̐��w�I����ɂ��ẮC���Z�H�w�y�ъm���ߒ��̃e�L�X�g���Q�Ƃ��Ē��������m�V�|�X�n�B�܂��C���c�̃u���b�N���V���[���Y�������Ɋւ���_�����V�~�����[�V�����y�уO���t�B�N�X���g���Đ������Ă���̂ŁC�{�_���������Ă�����̗����ɖ𗧂m10�n�B
�Q�|�P�DGiven Data ��Unknown
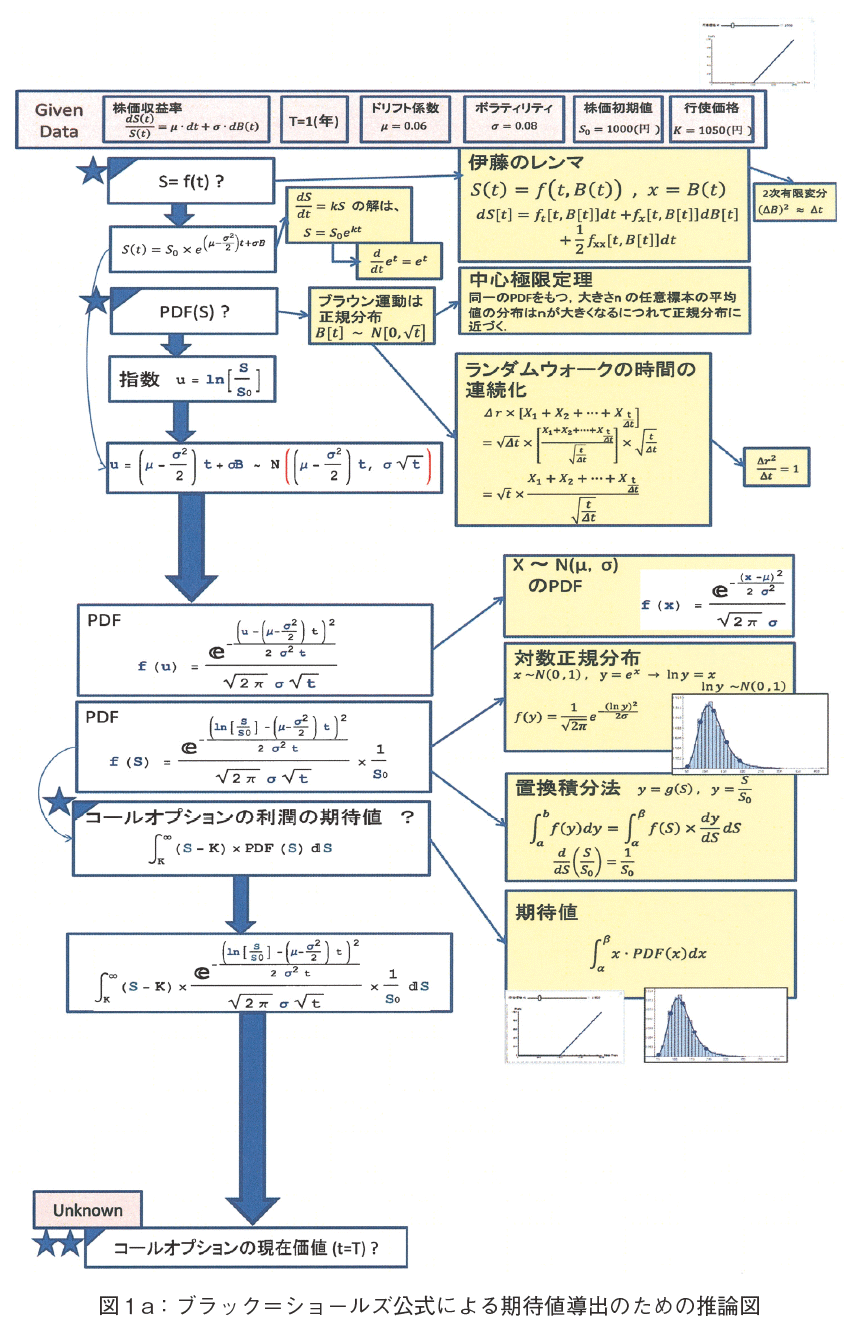
�I�v�V�����̊��Ғl���v�Z���镶�͑�Ƃ��āC����ݒ肵�C���� Given Data �� Unknown�i���ҋ��z�C���Ғl�j�̊Ԃ��Ȃ��C���_�ߒ���}�P�Ɏ������B�P���̐}�Ɏ��܂�Ȃ��̂ŁC�}�Pa �Ɛ}�Pb �ɕ����Ă���B���_�̃X�^�[�g���_�ŁC�o���_�ł��� Given Data �� Unknown ��F�����邱�Ƃ��d�v�ł���B��㈐��_���s���ߒ����C�ォ�牺�ɕ`����Ă���B�}�P�̃g�b�v�� Given Data �����X�g�A�b�v���Ă���BUnknown �͗����̊��Ғl�ł��邪�C�ŏI�I�ɂ����31.6135�~�Ƌ��߂���B
�@���̉�㈂̍ۂɗ��p���Ă����������уZ�I���[���E���Ɏ�����Ă���i�}�P�Q�Ɓj�B�u���b�N���V���[���Y�������̓��o�������Ă��Ċ����邱�Ƃ́C���o�v���Z�X�����ɒ������߁CUnknown �����Ғl�ł��邱�ƂɋC�t���Ȃ��w�����������Ƃł���B�����鑤���C���Ғl�����߂邱�Ƃ��ڕW�ł��邱�Ƃ��������ׂ��ł��낤�B
�@�A�u�_�N�V�����́C�p�[�X�iCharles Sanders Peirce�j�������B�p�[�X�̓A�u�_�N�V�����̐��_�`�����C�ȉ��̂悤�ɒ莮�����Ă���m11�n�F
�����ׂ����� C ���ώ@�����C
���������� H ���^�ł���CC �͓��R�̎����ł��낤�C
�y45 �Łz
�y46 �Łz
����āCH ���^�ł���ƍl����ׂ����R������B
C �Ƃ́C��X�̋^�O�ƒT���������N��������ӊO�Ȏ����܂��͕ϑ����̂��Ƃł���CH �� C ��������邽�߂ɍl����ꂽ�����ł���B
�@�A�u�_�N�V�����ɂ���āC��Ă���鉼���Ƃ��Ă��̖������߂���ƁC�u�I�v�V�����ɂ�闘���̊��Ғl���v�Z�ł���Ȃ�C�m���ϐ� X�i�����j�̊��`����сCX �̊m�����x�����v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v���o���̉��� H �ɑΉ�����B�������āC�ȉ��̂Q�̕����ڕW�������B
���@�����̊��`�����߂���
���@�����̊m�����x���iPDF: Probability Density Function�j�����߂���
�ȉ��ł͂��̕����ڕW���S�[���Ƃ��鐄�_�ߒ���_���Ă����B
�Q�|�Q�D�O��
�����̕ϓ������f�������邽�߂ɁC�����̔����ϓ��̓u���E���^����p���ĕ\�����邱�Ƃ͑O��Ƃ����B�u���E���^���i�����ɂ̓E�B�[�i�[�̊m���ߒ��j��\���L���Ƃ��āCB�it�j��p���Ă���B
�y47 �Łz
�������v���̊m������������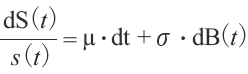 �́CGiven Data �Ƃ��ė^������C�Ƃ����B����
�́CGiven Data �Ƃ��ė^������C�Ƃ����B����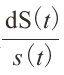 �͊������v����\���B�h���t�g�W�� �� �́C���ϐ�������\���B�{���e�B���e�B �� �͕W�����ł���B�u���b�N���V���[���Y�������̃��f���ł� �� ����� �� �͒萔�Ɖ��肵�Ă���B���̕������̍��ӂł́C���Edt �����ϓI������\���C���Edb�it�j�͗\�����ʔ����ϓ����u���E���^���ɂ��\���Ă���B
�͊������v����\���B�h���t�g�W�� �� �́C���ϐ�������\���B�{���e�B���e�B �� �͕W�����ł���B�u���b�N���V���[���Y�������̃��f���ł� �� ����� �� �͒萔�Ɖ��肵�Ă���B���̕������̍��ӂł́C���Edt �����ϓI������\���C���Edb�it�j�͗\�����ʔ����ϓ����u���E���^���ɂ��\���Ă���B
�@�܂��C���[���s�A���E�R�[���I�v�V�����̎d�g�݂��m���Ă��邱�Ƃ�O��Ƃ����B���̃I�v�V�����̏ꍇ�C�_�ɍs�g���i K �����肷��BK �͒萔�ł���B�������Ɋ��� S ���g���i������Ƃ��̂݁C�I�v�V�����ɂ�闘������������B�������s�g���i�������ꍇ�́C�����͂O�ƂȂ�B�����ŏ����ƁC�ȉ��̂悤�ɂȂ�B
�R�[���I�v�V�����̗����� max�i�O�CS�|K�j
���̃O���t�B�N�X�͔��c�̘_���m10�n���Q�Ƃ��Ē��������B
�@��L�̎����C�m���ϐ��̊��ł���B�m���ϐ���S�|K �Ƃ���BK �͒萔�ł���̂ŁCS �Ɋւ��Ċ��Ғl�̒�ϕ����s�Ȃ��悢�B����āCS �̂���ȏ�̊��`���v�Z���邱�Ƃ͕s�v�ł���B�������CS�|K ��PDF �����߂邽�߂ɂ́CS �̎��� t �Ɋւ�����`�����߂�K�v���o�Ă���B
�@�����ŁC�u���� S �̊��`���v�Z�ł��邱�Ƃ͓��R�̎����ł��낤�v�Ɩ��ݒ肵�C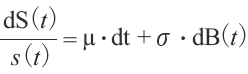 ��������S�it�j�����߂悤�Ƃ���B
��������S�it�j�����߂悤�Ƃ���B
�Q�|�Q�D�����̊��`
�����ڕW�Ƃ��āC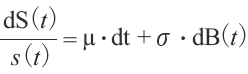 ��������S�it�j�����߂邱�Ƃ�ڕW�ݒ肷��B
��������S�it�j�����߂邱�Ƃ�ڕW�ݒ肷��B
�@���̊m�������������̓����́C�u���E���^�������Ƃ��Ċ܂ޓ_�ł���B�����ׂ������������Ƀu���E���^���i���m�ɂ̓E�B�[�i�[�v���Z�X�j�̍� dB�it�j���܂܂��̂ŁC�ʏ�̐ϕ������Ƃ͈قȂ�͎g���Ȃ��B�u���E���^�� B�it�j�́C�ǂ̂悤�Ȕ������Ԃ��Ƃ��Ă��C���̊ԂŁC��B�it�j�̐�Βl��ϕ�����ƁC������ɔ��U���Ă��܂��C�����ɂ������ł���B
�@�u���b�N����́C���̊m���������������������߂ɁC�u���E���^���Ɋւ�����������ɒ��ׂĂ������̂ł͂Ȃ����Ɛ��@�����B�uS �̊��`���v�Z�ł���Ȃ�C���� XX ���g���āC���̊m�������������������邱�Ƃ͓��R�̎����ł��낤�v�Ƃ����`���̉�����ݒ肵�C�����̉����̒�����C�ł������Ƃ��炵��������I��ł������ƍl������B�u���b�N����́C���̎��_�ŗ^����ꂽ�����f�[�^�ƌv�Z�ς݃f�[�^�C����сC�m���Ă����������уZ�I���[����g���Đ��������ɈႢ�Ȃ��B
�@�u���b�N����́C�����Ƃ��āC�ɓ��̃����}���b��I�ɍ̑������B���ɂ��\���͂������Ɛ��@�����B�Ⴆ�C�ɓ��̃����}�͂Q���ȏ�̍����̍��������e�C���[�W�J�ɂ��ߎ�
�y48
�Łz
���ł��邪�C�Ȃ��C����ɍ����̋ߎ�����p���Ȃ������̂ł��낤���C���X�ƍl���邱�Ƃ͂ł���B�����āC�����Ƃ��炵���iplausibility�j�C���؉\���iverifiability�j�C�P�����isimplicity�j�C�o�ϐ��̖ʂ��猟�����āC�ɓ��̃����}��I�������̂ł��낤�B�ɓ��̃����}���̗p����ƁC�������ʂƂ悭�����B����āC�ɓ��̃����}���̗p�������Ƃ͐������C�Ɛ��_�����̂ł��낤�B���̂悤�ɁC�b��I�ɍ̑����ꂽ�����̂Ȃ��ŁC�ł����ɓK�����������Ă��邱�Ƃ��A�u�_�N�V�����ł���B
�@�������C����͌㌏�m��ł���B�㌏�m��͘_���I�ɑÓ��ł͂Ȃ��C�㌏�m��͌��̉\��������B���̌����ł���ɂ����Ƃ��炵�������������������������C������̗p���ׂ��ł���B
�Q�|�R�D�����̊m�����x��
���Ɋ�����PDF ���ǂ��A�u�_�N�V�������邩�ɂ��čl����B�O��Ƃ��āC�u�u���E���^���ɂ�蓞�B���鋗���́C���K���z�ɏ]���v�Ƃ����Z�I���[�͒m���Ă�����̂Ƃ���B�����ł̐��_�́C�u�u���E���^���̐��K���z�Ɗ�����PDF ���W�Â��鐄�_�p�X������v�Ƃ����C�ォ�牺�ނ��̉�㈐��_�ƁC�����������L�т�t�������_�̗������ɍs���Ă���悤�Ɋ�����B�O������ɂ��C���ƂȂ鉼���̐����i�肱��C�������������Ă���悤�Ɋ�����B�܂�C�uS ��PDF ���v�Z�ł���Ȃ�C���� XX ���g���āC�w�� U �̐��K���zPDF�Ɗ֘A�t�����邱�Ƃ͓��R�̎����ł��낤�v�Ƃ����`���̉�����ݒ肵�C�����̉����̒�����C�ł������Ƃ��炵������ XX ��I��ł������ƍl������B
�@�ŏI�I�Ƀu���b�N���́C�ΐ����K���z���̗p�����B�ΐ����K���z�̊T�O�̗̍p�́C�ɓ��̃����}�̗̍p�ɔ�r���āC�K�R���������B��㈐��_�ŁC�ォ�牺�����ɁC���R�ȗ���œ��o�ł������Ɋ�����B�������C�����̎��f�[�^�̌��Ƃ��������𑽐��s���āC���ʂƂ��Ă��̑ΐ����K���z�̗̍p�����肵�����̂ƍl������B���͗e�Ղł͂Ȃ������ƍl������B
�@�ȏ�C�u���b�N���V���[���Y�������̓��o�͂ǂ̂悤�ɐ��_���ꂽ�����C�t�������_�����ł��ǂ��Ă݂��B�u�t�����ɉ�㈐��_��K�����āC���������Ă���v�Ƃ�����Ƃ��ẮC�iS�|K�j�̊��Ғl�̌v�Z�@���@S ��PDF�@���@S �̊��`�C�Ƃ������ꂪ����B���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���āC�����𗧂ĂĈ�����\�����Ȃ���CUnknown ���� Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����ƍl����B
�@�������C�m������������������ S �̊��`�����߂�ߒ��ɂ����ẮC���镔���ɂ��Ă͑O�������_���s���Ă���B�u�ɓ��̃����}��K������C���̂悤�� S �̊��`�����܂�v�Ƃ����O�������_�ł���B�܂��CS �� PDF �����߂�ߒ��ɂ����Ă��C���镔���ɂ��Ă͑O�������_���s���Ă���B�u�w�� U �̓u���E���^���܂� PDF �͐��K���z�Ȃ̂ŁCS ��PDF�͑ΐ����K���z�ƂȂ�v�Ƃ����O�������_�ł���B
�@�ł����ɓK����������I�����悤�Ƃ���ہC�ǂ̂悤�Ȑ��_���s���Ă��邩�́C���ۂ̂Ƃ��땡�G�߂��ĕs���ł���B�������C�S�̂̕��@�Ƃ��āC�u�t�����ɉ�㈐��_��K�����āC���������Ă���v�Ƃ����l���́C�u���b�N���V���[���Y�������̓��o�̉ߒ��ɂ����Ă��C�������ƍl������B
�y49 �Łz
�R�D�����̕���
�{�߂ł́C�u���b�N���V���[���Y���������o�̉�㈐��_�ߒ����C�������邽�߂̌����Q�ނ���B�}�P�̐��_�ߒ��Ŏg�������ɂ��Ă܂��q�ׂ�B�e�������ƂɁC���w�̕��삨��сC���̊w���ɂƂ��Ă̓�Փx�������B�܂��C�u�`�ŋ������o������C�w���ɗ��������邽�߂̃|�C���g�ɂ��ďq�ׂ�B
�@�@�ɓ��̃����}�F�m���ߒ��C����x
�@�ɓ��̃����}�͂Q�ϐ����̃e�C���[�W�J�ɂ��ߎ��ł��邪�C�Q���L���ϕ��̎��i�� B�j2 ≈ �� t ���x�[�X�ƂȂ��Ă���B������ؖ����邱�Ƃ͓���̂ŁC�V�~�����[�V�����ɂ��C���Ԃ̕������ׂ�������ɂ�āC��t �Ɏ������Ă����悤���������āC�ؖ��ɑウ�Ă���i�m10�n�Q�Ɓj�B�܂��C�������������ہC���̉��� e ���Ƃ���w�����ƂȂ邱�Ƃ�s�v�c�Ɋ����Ď��₳��邱�Ƃ�����B����͔������������������o�����Ȃ��ƁC�������Â炢�ӏ��ł��邩������Ȃ��B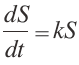 �̉���S = S0 ekt�����Ȃ����Ƃ��C
�̉���S = S0 ekt�����Ȃ����Ƃ��C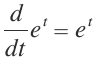 �̔����������O���t�B�N�X�Ō����Ȃ���������Ă���m12�n�B
�̔����������O���t�B�N�X�Ō����Ȃ���������Ă���m12�n�B
�A�@�u���E���^���̓��B�����͐��K���z�F���v��ʁC����x
�@���̃Z�I���[�́C���S�Ɍ��藝���g���ďؖ�����B����Ē��S�Ɍ��藝�𐳂����������Ă��Ȃ��ƁC���ʂƂ��āC���K���z�o����ߒ����B���ɂȂ�B�u���b�N���V���[���Y���������o�ł��̒藝���g���ۂ́C�ȉ��̂悤�ȕ��ϒl�Ɋւ���L�q������ق����C�������e�Ղł���B

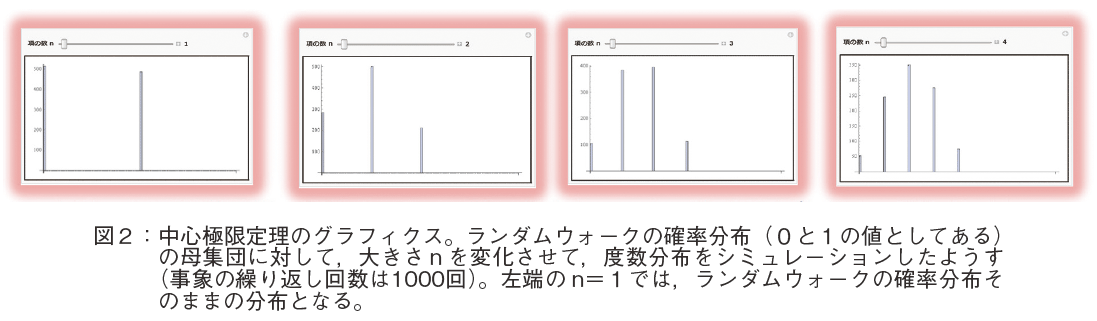
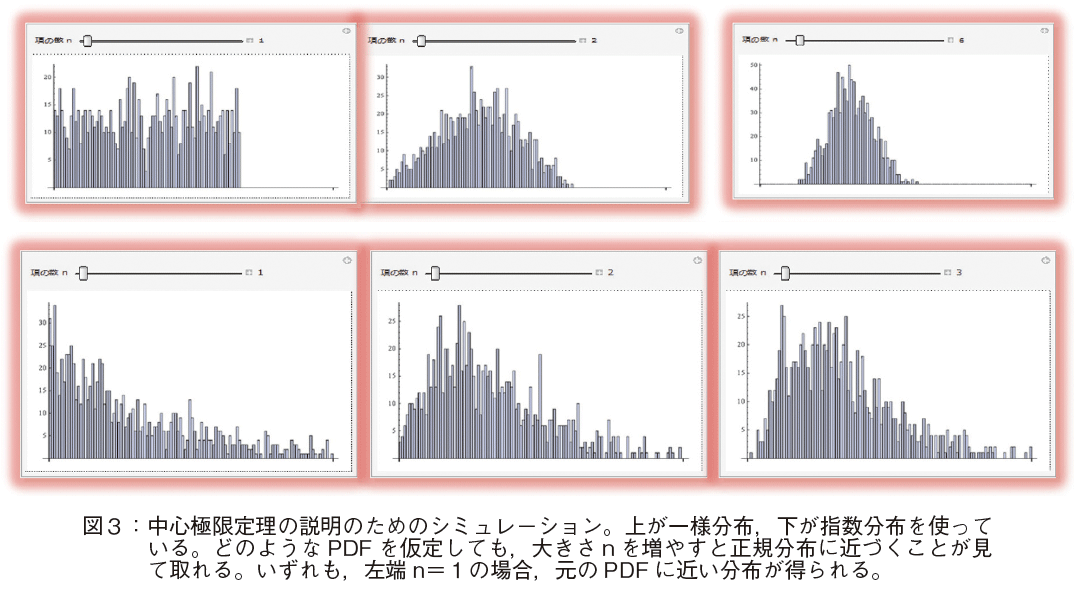
�܂��C���S�Ɍ��藝�𗝉����邽�߂ɁC�傫��n �̑����̂悤�����V�~�����[�V�����Ō�����ƌ��ʓI�ł���i�}�Q�Q�Ɓj�B�}�Q�ł́C�V���v�������_���E�H�[�N�D���f���̗��U�^�m���ϐ��� PDF ��p���āC�傫�� n ���P����S�܂ő�������l�q�������Ă���B�����_���E�H�[�N�D���f���ł́C��蓾��l�́{�P�Ɓ|�P�ł��邪�C�c�[���̓s����C�O�ƂP�Ƃ��Ă���B�傫�� n ��������ƁC���ϒl�̕��z�����K���z�ɋ߂Â��l�q�����Ď���B�}�R�ł͈�l���z�C�w�����z�̏ꍇ�ł��C���K���z�ɋ߂Â��l�q���������B���̐��K���z�ɋ߂Â��l�q�́C�X���C�_�[�ɂ��傫��n �����ۂɓ������Č���ƁC�{���ɂ悭�����ł���B
�y50 �Łz
�܂��C�����_���E�H�[�N�̎��Ԃ̘A�����𗝉����邽�߂ɂ́C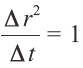 �̏ؖ����K�v�ƂȂ�B
�̏ؖ����K�v�ƂȂ�B
�@���̎��̏ؖ����C�u���E���^�������K���z�ł���|�C���g�ƂȂ邪�C���݂̒��҂̍u�`�ł́C��r �Ƈ�t �̎����̑��x�̐����͏ȗ����Ă��܂��Ă���B�o�ϊw���̍u�`�ɂ����ẮC�{�i�I�Ȋm���_�̏ؖ��͂ł��Ȃ����C��������o�Ƃ��ė����\�Ƃ���悤�ȊȌ��Ȑ����@��n�Ă��ׂ��ł���C����͉ۑ�ƍl���Ă���B
�B�@���K���z��PDF�F���v��ʁC����x
�C�@�ΐ����K���z�F���v��ʂł��邪�C���Z���w�C����x
�y51 �Łz
�D�@�u���ϕ��@�F��b���w�C���x
�E�@�A���^�m���ϐ��̊��Ғl�F���v��ʁC���x
�F�@�A�������@�F���Z���w�C���x
�G�@���݉��l�ւ̃f�B�X�J�E���g�F���Z���w�C���x
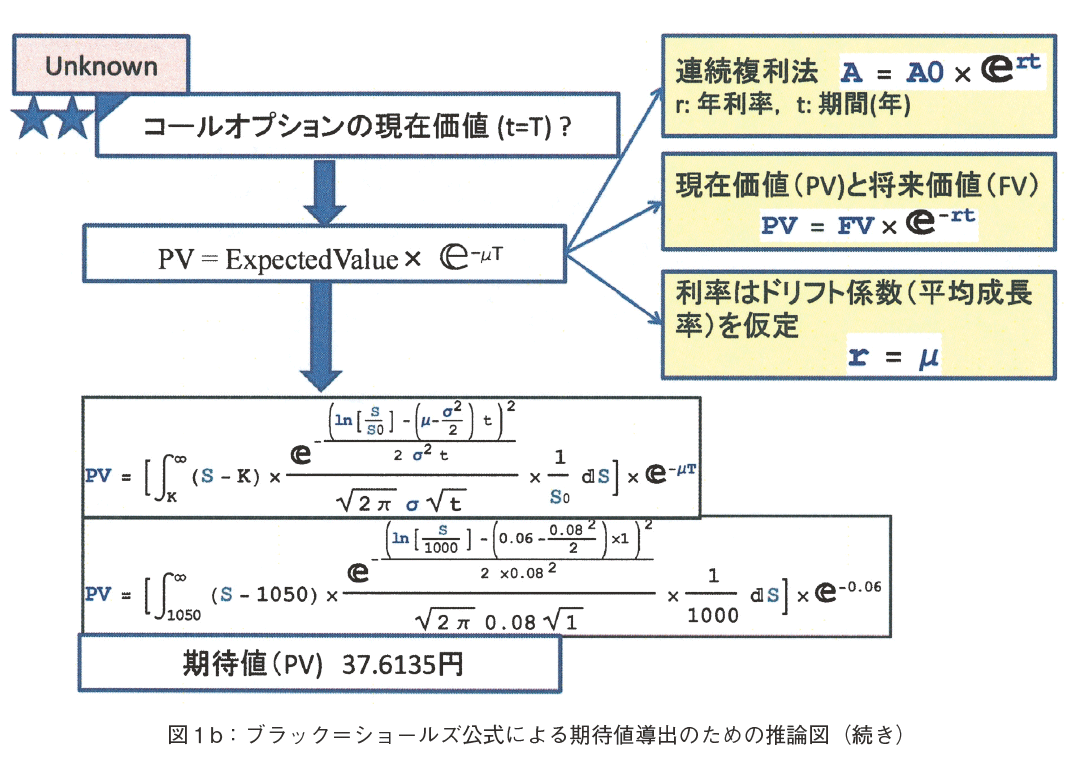
���Ғl�����܂�����ŁC�����ЂƂ��ׂ��������C���́C���݉��l�Ɋ�����������ł���B��ɋ��߂����Ғl�́C���� t��T �̂Ƃ��̉��l�ł���̂ŁC���݂���݂�C�������l�ł���B����āC��������K�v������B�S�̂̉�㈐��_�̗��ꂩ�猾���C�q�t���߂̕����ł���C���Z����̐l�ɂƂ��ẮC����e����ł��鏈���ƌ�����B�A�������C���݉��l�Ȃǂ̋��Z���w�ɂ��ẴO���t�B�N�X�ɂ�����́m12�n���Q�Ƃ��Ē��������B
�ȏオ�C�m���ϐ� S �Ɋւ�������̓��o�ŗp��������ł���B�������Ȃ���C�u���b�N���V���[���Y�̌����́C���� S �ł͂Ȃ��C�w�� u ��ϕ��ϐ��Ƃ��Ă���B
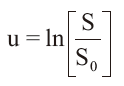
����āC���� S ��PDF �ł͂Ȃ��C�m���ϐ� u ��PDF ��p���āC���Ғl�̒�ϕ����s���B
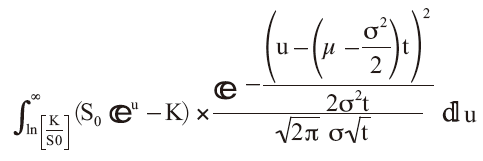
���̊��Ғl�����߂��ϕ��ł��邪�C��͓I�ɐϕ����v�Z����̂ł͂Ȃ��Ce �̎w���������܂Ƃ߂āi���Z�ł���j�C�ϐ� u �Ɋւ���Q���������C������������C�قȂ鐳�K���z��PDF �ɕό`����B��͓I�ɉ����Ă���̂ł͂Ȃ��B�ŏI�I�ɕW�����K���z�̃��C�u�����[���Q�Ƃ���`���ɂ���B�ȉ��̎����u���b�N���V���[���Y�̌����ł���B�����CN�ia�j�͕W�����K���z�Ŋm���ϐ��� a �ȏ�̒l���Ƃ�m����\�����ł���B
�ȉ��ɂ��̌����������B
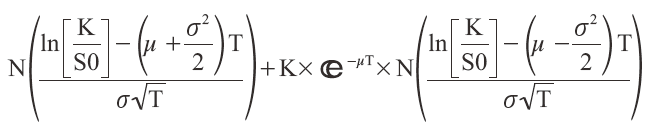
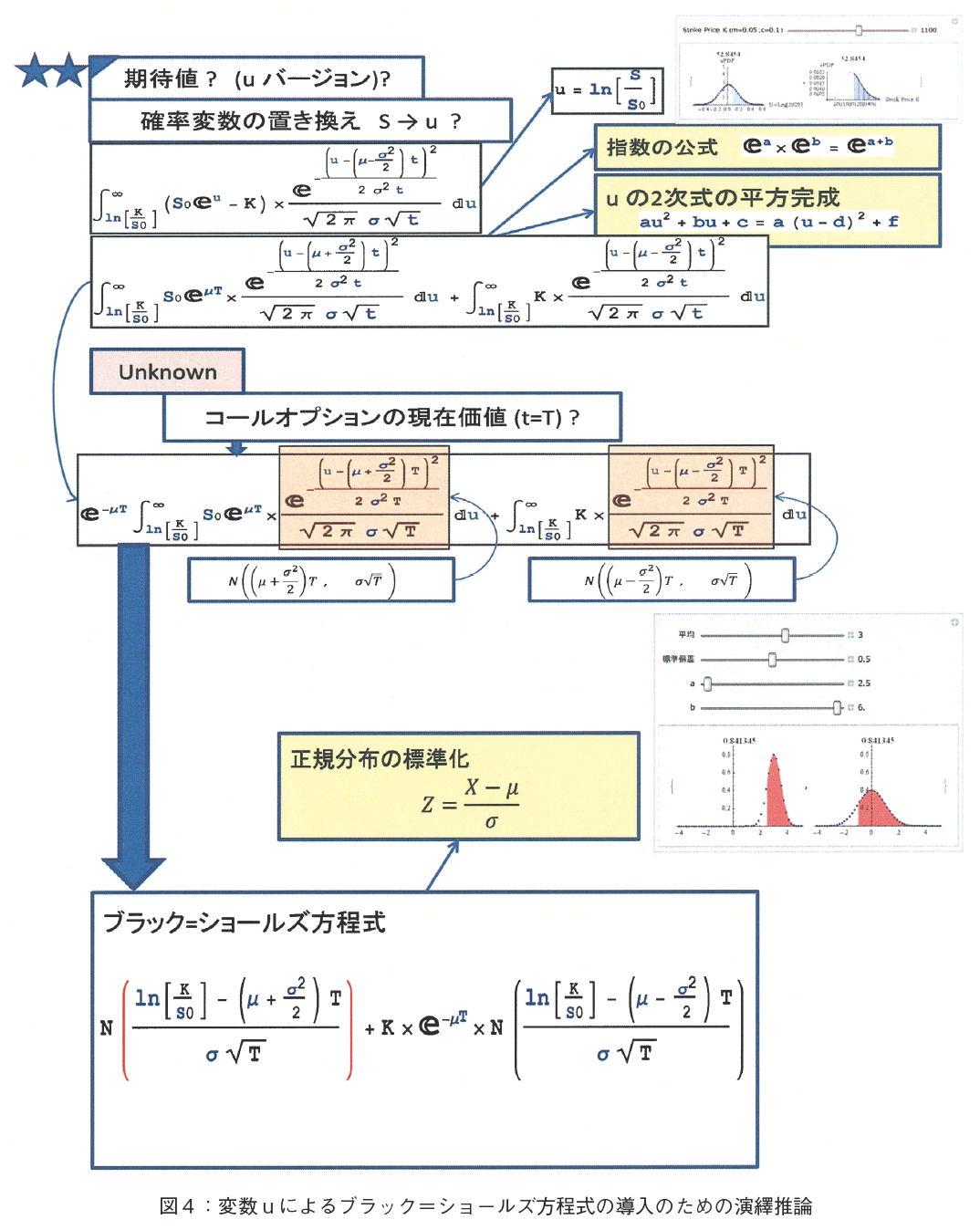
�}�S�ɁC�m���ϐ��� u �Ƃ����u���b�N���V���[���Y�������̓��o�̂��߂̐��_�ߒ��������B�O���͐}�P�Ɠ����ł���B�ȉ��ɂ��̉�㈐��_�𗝉����邽�߂ɕK�v�Ȍ��������X�g�A�b�v����B
�H�@���R�ΐ��̌����F��b���w�C���x
�I�@�w���̌����F��b���w�C���x
�J�@u �̂Q�����̕��������F��b���w�C���x�ł��邪�C�v�Z�͂��K�v�i�}�T�Q�Ɓj
�K�@���K���z�̕W�����F���v��ʁC���x�ł��邪�C�v�Z�͂��K�v
�y52 �Łz
�y53 �Łz
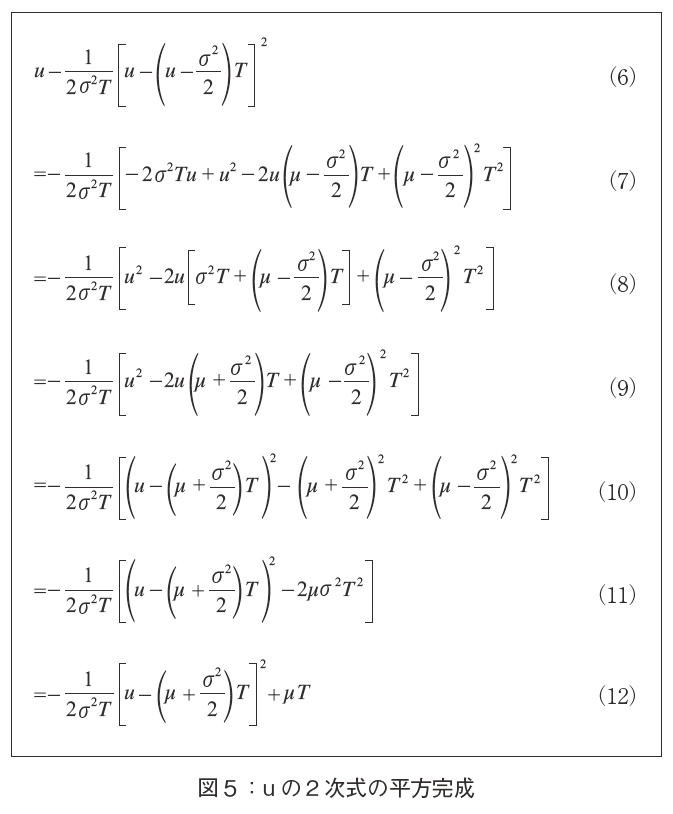
�S�D�l�@
���G�Ȑ��_�ߒ��̗�Ƃ��ău���b�N���V���[���Y�������̓��o�����������B���������������̗��_�́C�ȉ��̂悤�Ȃ��̂ł���B
�i1�j�g�����������m�ɂȂ�B
�܂��C�������ǂ̌����ɂ��ė������Ă��Ȃ��������m�ƂȂ�C���̕������w�K����� �悢���Ƃ�������B
�i2�j�t�������_�����邱�ƂŁC�A�u�_�N�V�����ɂ����Ăǂ����Ă��̌�����I�����������l�@���邱�ƂŁC���o�ߒ��̗������[�܂�B
�u���b�N���V���[���Y�̃��f���ł́C�����ϓ����f���Ƃ��ău���E���^����p���邱�Ƃ�O��Ƃ��Ă���B�u���E���^�����̗p���邱�Ƃ́C���K���z�����肷�邱�Ƃł���B�������C�����̌o�ϕ����w�ɂ����ẮC�x�L���z�ւƃ��f���g�����s���Ă���B���̐�삯�ƂȂ������̂́C�}���f���u���̈�A�̃x�L���z�̌����ł���B�}���f���u���́u�֒f�̎s��v�m13�n��
�y54
�Łz
���ŁC�q�ׂĂ���F�u���낢��Ȏs��̉��i�̕ω����ׂ������ׂĂ݂�ƁC���K���z�������삪�����ƒ����x�L���z�ɒ��ڂ��W�܂��Ă��܂����B�i�r�������j�@���i�ω��͐��K���z�ł͂Ȃ��ߋ��̃f�[�^�ƓƗ��ł��Ȃ��Ƃ������̎咣�́C���ł͉��S�l���̃G�R�m�~�X�g��s��A�i���X�g�����̑Ó����͂ɂ��ĔF�߂Ă��܂��B�v
�@�������āC���݂̋��Z���w���̑��̕���ɂ����ẮC�x�L���z���L���g����悤�ɂȂ����m14�|18�n�B�������C���K���z�����肵�Ă��Ă��w�ǂ̃}�[�P�b�g�̏ꍇ�͂��܂��@�\����B��肪�N����̂͋H�ɋN�����ϓ��̏ꍇ�ł���B���̂悤�ɁC�A�u�_�N�V�����ɂ����āC�ł������Ƃ��炵�������������Ă����Ƃ�����Ƃ́C�A�ȂƑ�����Ƃł���C��l�̌����҂̐l�������Ŋ���������̂ł͂Ȃ��B�O��ƂȂ郂�f�����̂��C�g�������ׂ��ł���C�Ƃ������Ƃ����邱�Ƃ�S�ɗ��߂C�܂�C�O����������^�I�Ɍ���ԓx��{�����Ƃ��C�u���b�N���V���[���Y�������̓��o�̐��_�ߒ������ނɊw�ׂ�ƁC�l����B�����������f���\�z�̗�Ƃ��āC�u���b�N���V���[���Y�͊Ȍ��ň����₷�������ł���̂ŁC���Z���w�̋��ނƂ��ēK���Ă���B
�@���ۂɁC��㈐��_�@�Ńu���b�N���V���[���Y���������u�`�����Ƃ��̊w���̔����ɂ��ďq�ׂ�B2013�N�V��22���C������w�������H�w���ŁC��w�@����ΏۂɂP���Ԕ��ŁC�u���b�N���V���[���Y�������̓��o���u�`�����B�o�ϐ��w�͏��߂ĂƂ������H�n��w�@���ł���B�t�������_����ەt���邽�߁C�͂��߂Ɂu��i����I�v�V�����̉��i��������ɂ��ׂ����C���Ғl��]�����Ăق����C�ƌ����܂����B���Ȃ��́C�ǂ̂悤�Ɋ��Ғl���v�Z���Ă����܂����H�v�Ƃ�������̖₢�|�����s�����B����͎����Ő��_���s���g���K�[�ƂȂ�ƍl����B
�@�u�`�̌�C�q�A�����O�������ʁC�ȉ��̂悤�Ȋ��z���B�u�w���̂Ƃ��w���e������O���t�B�N�X�ł̕��K�͂킩��₷�������B��㈐��_�@�͘b�̗��ꂪ�킩��₷���C�������g���Ă݂����Ǝv�����v�u��㈐��_�@�͂ƂĂ�������Ղ��Ǝv�����B���X�̒m���s���ŕt���Ă����Ȃ����낤�ƍl���Ă������C���Ƃ������ł����B�ڂŌ��čl���邱�Ƃ��ł����̂ŁC�������i�Ǝv���v
�@�O���t�B�N�X�ɂ�鐔�w�藝�̐����̕�����Ղ��C��㈐��_�@�̘b�̗���̕�����Ղ��ɑ��āC�m��I�ȕ]��������ꂽ�B��㈐��_�@���g�����Ƃɂ��C�o�ϐ��w�̌o���̂Ȃ����H�n��w�@���ɂ��C�u���b�N���V���[���Y�������𗝉����Ă��炤���Ƃ��ł���C�Ƃ����育�����邱�Ƃ��ł����B
�T�D�܂Ƃ�
�o�ϐ��w����@�̉�㈉ߒ������߂邽�߂ɂ́C��㈁C�A�[�C�A�u�_�N�V�����̂��ׂĂ��I�ɋ�g���Ďv�l���s���Ă���ƁC��X�͍l���Ă���B���̎v�l�̉ߒ��ɂ����ẮC�A�u�_�N�V�����ɂ���āC�����𗧂ĂĈ�����\�����Ȃ���CUnknown ���� Given Data �����ɂނ����āC�t�����ɉ�㈐��_��K�����āC���������Ă���̂ł͂Ȃ����ƍl����B���̉����������邽�߂ɁC�u���b�N���V���[���Y�������̓��o���ɂƂ�C���̐��_�ߒ����������B���镔���ɂ��Ă͑O�������_���s���Ă���B�������C�S�̂̕��@�Ƃ��āC�u�t�����ɉ�㈐��_��K�����āC���������Ă���v�Ƃ����l���́C�u���b�N���V���[���Y�������̓��o�̉ߒ��ɂ����Ă��C��Ɋւ��Ă͐������ƍl������B�܂��C����������̓I�ȗ���L�^���邱�ƂŁC���_�̌����҂Ɏ��ۂ̎����ł���K���ł���B
�y55 �Łz
�o�ϐ��w�̖��ł́C�ǂ̂悤�ȃ��f������邩���d�v�ƂȂ�B�����̃��f���ɉ��^�I�ɂȂ�C���f�����g�����邱�ƂŁC���悢�v�Z���ʂ�������B���̈Ӗ��ł��C�b��I�ɉ������̗p���C�����̉����̒�����ŗǂ̂��̂�I��ł����A�u�_�N�V�����̃v���Z�X���C�ǐՂ��邱�Ƃ́C����I���ʂ������ƍl������B����Ƃ��C���_�@�Ɋ�Â����w����@�ߒ��̌�����i�߂Ă��������B
�Q�l����
�m�P�n P. Stanworth and Y. Shirota, �gReview of the �gWeb: How�QSolveIt�h Website,�h Gakushuin Economics Papers, vol. 50, pp. 1-18, 2013.
�m�Q�n Y. Shirota, T. Hashimoto, and P. Stanworth. Knowledge Visualization of Deductive Reasoning for Word Problems in Mathematical Economics. Lecture Notes in Computer Science (LNCS) series (DNIS 2013 Vol. LNCS 7813), 2013.
�m�R�n ���c�R�����C���{���q�C�g�o�c���w����@�̂��߂̉�㈐��_�x�����ލ쐬�c�[���h�C�{�K�@��{�S�Z�_�W�Cvol. 48�Cpp. 303-311�C2011�B
�m�S�n ���c�R�����C�g�o�c���w����@�ɂ����鉉㈐��_�Ɋւ���l�@�h�C�{�K�@��{�S�Z�_�W�Cvol. 49�Cpp. 85-98�C2012�B
�m�T�n Y. Shirota and T. Hashimoto, �gPlausible Deductive Reasoning Plan for Business Mathematics Learners - Solution Plan Graph Generator -,�h Proc. of 2nd Uncertainty Reasoning and Knowledge Engineering (URKE2012), Jakarta, August 14-15, pp. 5-8, 2012.
�m�U�n A. Brown and P. Mehrling, Fischer Black and the Revolutionary Idea of Finance Wiley, 2011.
�m�V�n N. Chriss, Black Scholes and Beyond: Option Pricing Models: McGraw-Hill, 1996.
�m�W�n �����]�C����m���ߒ��F�����}���C2003�B
�m�X�n �����]�C�����]�̊m���ߒ����I�����F�����}���C2011�B
�m10�n ���c�R�����C�g�u���b�N���V���[���Y�������Ɋւ���V�~�����[�V�����ƃO���t�B�N�X�ɂ��l�@�C�h�{�K�@��{�S�Z�_�W�Cvol. 49�Cpp. 251-260�C2013�B
�m11�n �Đ��T��C�p�[�X�̋L���w�F�������[�C1981�B
�m12�n ���c�R�����C���{���q�C�э��C�����ė������鐔�w����i e-Book�j�F�I���C���[�E�W���p���C2012�B
�m13�n �x�m���EB�E�}���f���u���C���`���[�h�EL�E�n�h�\���C�����G���i�Ė�j�C�֒f�̎s�� �t���N�^���ł݂郊�X�N�ƃ��^�[���F���m�o�ρC2008�B
�m14�n D. Sornette, Why Stock Markets Crash - Critical Events in Complex Financial Systems -: Princeton University Press, 2003.
�m15�n D. Sornette, Critical Phenomena in Natural Sciences - Chaos, Fractals, Selforganaization and Disorder: Concepts and Tools -: Springer, 2003.
�m16�n P. Ball, Why Society is a Complex Matters - Meeting Twenty-first Century Challenges with a New Kind of Science -: Springer, 2003.
�m17�n �R�G���C�ƕx�m�C�r�c�T��C���n�j�C�����`�v�C�o�ϕ����w�F�����o�ŁC2008�B
�m18�n �R�G���C�ƕx�m�C�r�c�T��C���n�j�C�����`�v�C�p���[�g�E�t�@�[���Y����Ƃ̋��S�ƂȂ���̉Ȋw�� �F���{�o�ϕ]�_�ЁC2007�B