新しいページ 1

【83 頁】

交渉のモデルとしての消耗戦をめぐる３つの謎

神戸　伸輔^{* **}

Abstract

消耗戦モデルは交渉のモデルとしてしばしば使われてきた。しかし，もともと生物の駆け引きの分析のために考え出されたモデルを人間の交渉の分析に当てはめるために，いくつかの強い仮定が置かれている。この小論は，これまでのモデルが現実の交渉をうまく近似しているかを吟味する。３つの大きな疑問を立て，さらにそれらを小さな疑問に分解し，疑問に一つずつ答える形で定式化の妥当性について検討する。

１．イントロダクション

消耗戦（war of attrition）は交渉や企業間の駆け引きのモデルとしてしばしば使われている。モデル自体はとてもシンプルで，それでいて交渉や駆け引きの重要な側面，つまり，「どちらも早く妥結したいが，できれば自分に有利な条件で妥結したい」という利害の一致と相反の同居する状況をうまく表している。本小論では，このモデルの適用される対象として，交渉の分析に焦点を当てて分析していく^1）。交渉の分析においては，動学モデルである消耗戦は，時間をかけて交渉する状況の分析に適切なモデルであると考えられている。
　もともとのモデルは，メイナード＝スミスが生物の駆け引きにおいてどちらが譲歩するかを分析するために作ったものである（Maynard Smith, 1974）。均衡では，プレイヤーは時間を通して確率的に譲歩（＝妥協）する。これは，「完備情報のもとでも妥協がすぐに起こらない」ことを示している。この性質に注目し，消耗戦のモデルは，労使交渉などでお互いが自身の要求にこだわって長々と交渉する状況をモデル化する際に使用されてきた^2）。交渉がすぐに決着【84 頁】しないという非効率性を説明するモデルとなっている。ただ，生物の駆け引きの状況をモデル化したものを，人間間の駆け引きに当てはめるには，いくつかの仮定を置くことになる。それらの仮定は，しばしば暗黙のうちに置かれており，あまり吟味されてこなかった。この論文では，それらを明示的に議論することを目的とする。細かい仮定も含めれば議論の対象とすべきことはいろいろあるが，ここではそのうち主要なものとして以下の３つを考える：（１）どうやって一つの要求にコミットするか，（２）どうして非整合（incompatible）な要求がなされるか，（３）なぜ永久に続かないか。これらについて検討することで，消耗戦を交渉の分析に使うことにおいて，方法論的な基礎を固めることを意図している。
　本小論の構成は以下のとおりである。第２章で基本となる２種類のモデルを導入する。それらを基に，第３章から第５章において，上で述べた３つの問いを順に検討していく。第６章は最近の展開について簡単に触れ，第７章は結語である。

２．基本となるモデル

消耗戦のモデルでは，継続利得が時間の経過とともにゼロ以下に減っていくか^3），それとも常に正の値を取るかで，均衡での行動が大きく異なってくる。本小論では，常に継続利得が正のモデルのみを取り上げる。多くの交渉の状況においては，継続利得が常に正であるとの想定は自然であるからである。
　この章では継続利得が常に正であるような消耗戦のモデルとして，オリジナルモデルと評判モデルを導入する。これら２つのモデルが，以下の議論の基本モデルとなる。

オリジナルモデル

メイナード＝スミスのモデルを交渉の局面に当てはめたモデルとして以下のものを考える。プレイヤーはAとBの２人とする。連続時間で無限期間を考え，時間［０, ∞）の中でゲームがプレイされる。選択肢は｛α，β｝の２つであり，αを選ぶとAは取り分としてx_A を受け取りBは１－x_A を受け取る。一方，βを選ぶとBは取り分としてx_B を受け取りAは１－x_B を受け取る。ここで，x_A＋x_B ＞１を仮定する。この仮定の下では，x_A＞１－x_B と x_B＞１－x_A が成り立つ。つまり，プレイヤーAはαをβより好み，逆に，プレイヤーBはαよりβを好むことになる。このように選択肢間で利害対立があることが，消耗戦の基盤となる。相手の好む選択肢を受け入れることを「妥協」と呼び表す。プレイヤーi ∈｛A，B｝の利得は，妥協が時間 t 【85 頁】でおこり，そこでの彼の取り分がy_i の時，y_ie^－rit で与えられる。r_i は割引率である。それぞれのプレイヤーは期待利得の割引現在価値の最大化を目指す。
　それぞれのプレイヤーはどの時点で妥協するかを決める。どちらかのプレイヤーが相手の好む選択肢を受け入れればゲームは終了し，受け入れられた選択肢がそれぞれの利得を決める。同時に両者が妥協したときは，確率１／２でどちらかの選択肢が選ばれる。
　このゲームには多くのサブゲーム完全均衡が存在する。（以下で均衡というときは，完備情報ゲームではサブゲーム完全均衡を考え，不完備情報ゲームでは完全ベイジアン均衡を考える。）どちらかがすぐに妥協することも均衡である。また，１未満の確率でどちらかが妥協した後で，以下に述べる混合戦略を取ることも均衡になる。
　興味深い均衡は，どちらもすぐには妥協せず，妥協する時間を確率的に選ぶ均衡である。そこでは相手のプレイヤーの妥協する確率を前提とすると，プレイヤーはすぐに妥協しても待ってから妥協しても利得がちょうど同じになっている。この均衡では，ゲームは確率的に終結し，確率１でいずれ終わるが，どんなに長い期間を取っても終わらない確率が正となる。具体的に，時間当たりの妥協する割合を求めてみよう。プレイヤーAはすぐに受け入れることで１－x_B を得る。消耗戦の続いている間は正の確率で妥協を選択するが，それはどの時点でもそこで評価したそれ以降の利得が，すぐ妥協することからの利得である１－x_B と一致することを意味する。一方，プレイヤーBが妥協する時間当たりの割合をρ_B で表すと，△だけ待ってから受け入れるとその間にρ_B △の確率で相手が妥協する。その時はx_A の利得を得ることができる。△だけ待っていても，１－ρ_B △の確率で，プレイヤーBは妥協しない。この場合，プレイヤーAは△後に再び消耗戦の状況に直面する。上述したようにその時点での利得は１－x_B となる。消耗戦の続いている間は，プレイヤーは妥協するタイミングについて混合戦略を取るから，どの時点で妥協するとしても無差別になる必要がある。そこで，すぐ妥協することからの利得と少し待ってから妥協することの利得が等しくなり，以下の等式が成立する。（逆に，この等式が成立すれば，時間を少しずつずらす連鎖を考えることで，どの時点で妥協するとしても無差別になる。）

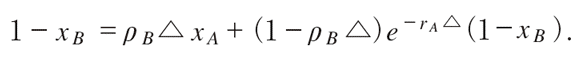
これを解いて，

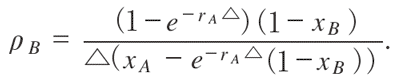
△をゼロに持って行き，ロピタルの定理を使うと，

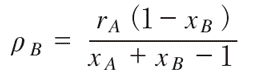
を得る。プレイヤーAが妥協する時間当たりの割合も同じように求められる。

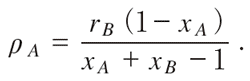
評判モデル

オリジナルモデルをゲーム理論を使って定式化し，サブゲーム完全均衡を求めると，対称な均衡以外にも，さまざまな非対称均衡が存在することが分かった。非対称均衡の中には，交渉がすぐに妥結するものもある。どの均衡が起こるかはオリジナルモデルでは説明できず，何が【86 頁】起こるか予測できないという意味で，複数均衡の存在はこのモデルの欠点であると考えられている。完備情報であるので，不完備情報のもとでのリファインメントは，この状況では有効でない。そこで考えられたのが，非合理的なタイプが存在する可能性を導入し，評判（reputation）がコミットメントを可能にするモデルである。Abreu and Gul（2000）は，一定の確率で決して妥協しない頑固な（stubborn）タイプがいる場合，消耗戦は唯一の均衡を持つことを示した^4）。しかも，この均衡では，必ず正の確率で消耗戦が起こり，オリジナルゲームのようにどちらかが確率１でゲームの初めに妥協することは起こり得ない。利害の対立が必ず消耗戦につながることを明確に予測した点で，何が消耗戦を引き起こすかの議論に一つの答を出している。
　プレイヤーi が頑固タイプの場合，必ず自分に有利な選択肢を要求し決して相手の要求を受け入れないとする。プレイヤーi がそうである確率をz_i とする。柔軟タイプはどんな要求もできるし，また相手のどんな要求も受け入れることができる。プレイヤーにこれら複数のタイプがありそしてタイプに関する情報が私的情報であるという仮定以外は，評判モデルの定式化（タイミングや柔軟タイプの利得）はオリジナルモデルと同じである。
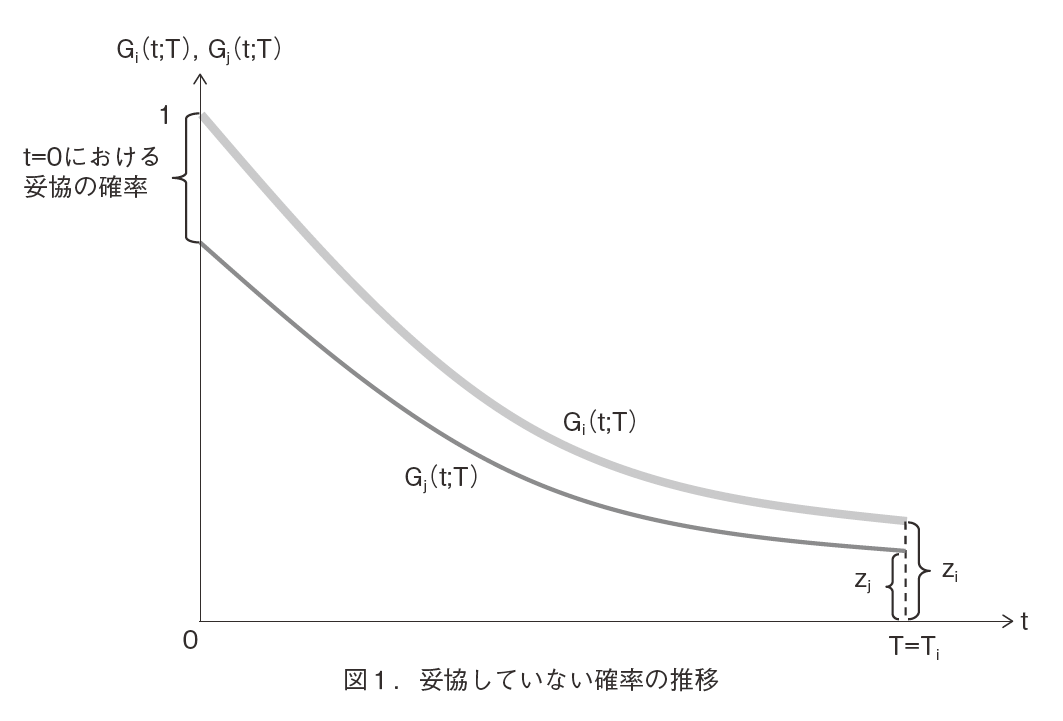
　均衡では，柔軟タイプが残っている限り，時間当たりρ_i の割合でプレイヤーi は妥協する。この割合はオリジナルモデルのものと同じである。一定の割合で妥協していくと，やがて柔軟タイプは必ず妥協し，頑固タイプだけが残ることになる。プレイヤーi の柔軟タイプが時間Tまでに必ず妥協するとして，時間t においてプレイヤーi が妥協していない確率をG_i （t ; T ）で表す（この確率は交渉の開始時で測ったときの評価である）。すると，G_i （t ; T ）は以下の式で特徴づけられる。

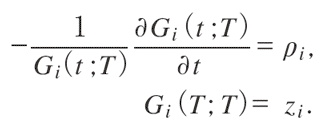
これを解くと，

となる。つまり，プレイヤーi が時間t において妥協していなく残存している確率は指数的に減衰し，時間T には頑固タイプだけが残る。ここで，最初に全く妥協しないで消耗戦を始めたとき，プレイヤーi の柔軟タイプが妥協する可能性のある最終の時間をT_i とする。T_i は１＝G_i （0; T_i ）の解であるから，

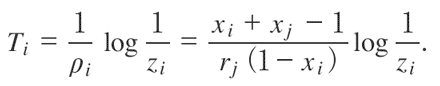
消耗戦が続く間はお互いに正の割合で妥協をするので，両プレイヤーの柔軟タイプはある同じ時間まで確率的に妥協をし続け，そして，その時間までに必ず妥協することになる。これを実現するため，T_i ＜ T_j のとき，プレイヤーj は t ＝０において正の確率で妥協し，短いほうの時間T_i までに，両方のプレイヤーの柔軟タイプが必ず妥協することになる。プレイヤーj が t ＝０において妥協していない確率は１より小さいG_j （0; T_i ）となり，１より減っている差分が，t ＝０でプレイヤーj の柔軟タイプが妥協する確率となる（図１参照）。そこで，t ＝０における【87 頁】妥協の確率をP ^maとすると，

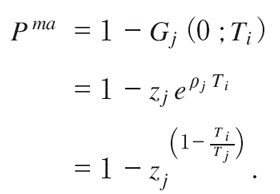
ちなみに，T_i ＝ T_j のときは誰も最初に正の確率で妥協せず，T ＝ T_i ＝ T_j となる。

最初の要求を選べるモデルと要求を変えられるモデル

上記の２つのモデルでは，選択肢は事前に与えられていて，かつ，それらを途中で変えることはできないと想定されていた。実際の交渉では，ある程度は，最初の要求を自由に選ぶことができる。上述のモデルにおいて，交渉の開始時に要求を選べる手番を付け加えたモデルを，以下では最初の要求を選べるモデルと呼ぶ。
　最初の要求は何らかの外生的理由で与えられたとして交渉が始まった場合も，交渉の途中で要求を変えることも実際の交渉ではよくみられる。上記の２つのモデルに付け加えて，要求を途中で変更できるように仮定したモデルを，以下では要求を変えられるモデルと呼ぶ。

３．どうやって一つの要求にコミットするか

オリジナルモデルでは，相手の要求を受け入れるのでなければ，それぞれのプレイヤーは一つの要求をし続けると想定されている。人間以外の生物の場合は，選択肢が固定されている状【88 頁】況が一般的であると想定できるが，人間同士の交渉の場合，選択肢を交渉の中で新たに作り出していくことは，交渉人に期待される重要な役目である。たとえば，お互いが自国の主張に固執し長々と続く外交交渉は，消耗戦の定式化がふさわしいと考えられがちであるが，背後では双方が受け入れられるような代替案の探り合いが行われていることが多い。そして，実際の解決はどちらかが妥協して相手の要求を受け入れることでなく，何らかの方法で提出された中間点において起こることが多く，そこでは消耗戦の定式化は適切ではない。本章では，最初の要求は外生的に与えられるとして，その後は要求を途中で変えられるモデル（前章で導入した要求を変えられるモデル）を基に議論する。最初に，プレイヤーがどうやって最初に出した要求に固執するかというコミットメントの仕組みについて議論する。これに関連する問いとして，コミットする対象が一つの要求でなく，一定の要求ルールであるときに何が起きるかを考える。要求のルールの例としては，たとえばある一定の比率で要求を引き下げることなどである。

Q．一つの要求を変えない状況にはどんなものがあるか

初めから選択肢が２種類しかなくその中で利害対立があるとき，消耗戦が起こる可能性は容易に想像できる。しかし，選択肢が多数ある一般の交渉において消耗戦が起こるとすれば，それぞれのプレイヤーが一つの要求にこだわり，途中でそれを変更しない理由があるはずである。特にお互いにとって継続利得より高い分割があるのにそれが提案されないということは，提案するとかえって不利になるか，あるいは提案しても必ず拒否されると思っているかのどちらかである。いずれにせよプレイヤーが自分の要求にコミットしていることになる。このコミットメントの力はどこから来るのか。
　連続時間のオリジナルモデルでは，消耗戦が始まるとそれぞれのプレイヤーの利得は相手の利得を受け入れる妥協時の利得と常に一致する。言いかえれば自分の要求は自分の利得に影響しない。要求を変えられるモデルにしたとしても，消極的な意味で，プレイヤーには自分の要求を変えないインセンティブがある。しかし，この状況はモデルを逐次手番に変えると大きく変わってくる。逐次手番の場合にはRubinstein（1982）の交互提案モデルで示されたように，一般に交渉はすぐに解決することになり，消耗戦は発生しない。つまり，固定した要求を言い続けることは，特定のモデル（連続時間で同時手番）では均衡であり得るとしても，一般の状況では必ずしも均衡で支持できない。その意味で，モデルの定式化として納得できるものではない。
　現在知られているモデルの中で，手番の詳細に依存せずに，プレイヤーが要求を変えられる状況でも一つの要求に固執するものは２つ知られている。
　一つは，評判モデル^5）であり，頑固なタイプはある要求にコミットして心理的にその要求未満の要求を受け入れられないと想定する。なお，ここでは最初の要求は外生的に与えられているとする。プレイヤーが確率１でこのタイプであるというのは現実的でない^6）。一方，そのよ【89 頁】うなタイプが小さい確率でいることはかなり現実的である。このモデルでは，要求を変えた瞬間に相手に頑固タイプでないことがばれてしまい，それは相手の要求を即座に受け入れることにつながる。そこで，プレイヤーたちは相手の要求を受け入れるか，それとも自分の要求を繰り返し続けるかという二者択一の状況になる。
　もう一つは，留保水準に関して不完備情報のある状況で，コース予想（Coase conjecture）が成立する状況である（Gul et al., 1986）。コース予想の示すことは，一方のプレイヤーの利得がはっきりわからない場合，要求が十分頻繁になされる状況では，そのプレイヤーは自分にとって最も有利なタイプのふりをし，均衡では相手はその行動を受け入れざるを得ないということである。この状況では，利得の分からないプレイヤーはあたかも一つの利得に固執しているようにふるまう。もう一方のプレイヤーが一つの要求を掲げ，確率的に妥協する戦略を取ると，消耗戦が発生する。ただし，コース予想がはっきりと成立することが分かっている状況は，一人のプレイヤーに不確実性が存在する場合であり，二人のプレイヤーが共に要求に固執することの説明に使えるかはよく分かっていない。
　あまり議論されていないが，要求を変化させるコストも消耗戦をもたらす可能性がある。これに関連する研究として，Crawford（1982）は，コストをかけて１回だけ要求を取り下げるかどうか決められるモデルを分析している。自然な疑問は，そのような状況が連続時間の中で起こったらどうなるかである。要求を変えるコストを嫌ってお互いに同じ要求をし続ければ，消耗戦が起こることが予想されるが，現在のところこのような動学への拡張の分析はされておらず，今後の展開が待たれるところである。

Q．要求を変化させないことはメリットがあるか

要求にコミットすることがどのように交渉力に影響するかを調べるため，この行為を２つの別な行為に分解する。
　一つは，それ未満の相手の要求を受け入れられないことにコミットすると解釈することである。もう一つは，それ未満に自分の要求を引き下げないことにコミットすることである。Rubinstein（1982）による交互提案モデルで，それぞれの戦略がどのような結果につながるか見てみよう（Kambe, 2013a）。
　まずは，それ未満の相手の要求を受け入れられないことにコミットする状況を分析しよう。ただし，このプレイヤーも自分の要求を変えることはできる。このとき，均衡ではコミットしたプレイヤーは少なくともその値の利得を得ることができる。（自分の提案から始まればそれよりも高い利得が得られる。）
　次に，あるプレイヤーが要求を変化させないことにコミットできる状況を分析しよう。ただし，消耗戦で仮定するように，このプレイヤーも相手の要求を受け入れることはできる。このようなコミットメントをすることはメリットがあるか？均衡を求めると，このようなコミットメントは，それをするプレイヤーの交渉力を上げるどころか，劇的に引き下げてしまう。つまり，相手が柔軟に要求を変えられるときに，自分だけ要求を固定することにコミットすること【90 頁】は，不利であることが分かる。
　この分析から，ある要求にコミットすることが交渉力を増すのは，要求を固定することからではなく，相手に有利な要求を受け入れないことからであると結論できる。
　なお，前者のコミットメントでは，要求が十分頻繁に行われる状況では，自分の提案からスタートしても，自分の利得は自分の要求を受け入れてもらうことにほぼ等しくなる。それより高い要求をすると，相手はそれを拒否して，相手の提案の番でコミットされた要求水準に対応するオファーをすることができるからである。こうして，誰の提案から始まっても，コミットしたプレイヤーは，コミットした水準に対応する利得を得ることになる。つまり，十分に頻繁に提案がなされる状況では，一定の提案以下では受け入れないことにコミットすることと，一定の提案をし続けてかつそれ以下では受け入れないことにコミットすることは，近似的に同じものとみなすことができる。

Q．頑固なタイプについて

評判モデルの定式化の弱点は，頑固なタイプはどんなタイプかということが外生的にしか与えられないことである。実際の交渉では，一見頑固に見えるプレイヤーがある種の駆け引きに応じることがある。特に，顔を立てた形（評判をあまり下げないような言い訳を与えること）での妥協はしばしばみられる。つまり，頑固なタイプも，ある状況では要求を変えられると想定することが現実的である。
　もう一つのポイントは，上の議論からわかるように，頑固なタイプに不可欠なことは，相手の要求を受け入れられないことであり，自分の要求を変えないことではないことである。そこで，理論的な観点からも，評判を維持しつつ途中で要求を変える状況を議論する必要がある。要求を完全に自由に変えられるというのでは，定式化ができないし，また現実的でもないので，多少は要求を変えられる状況を定式化する必要がある。そのような状況としては以下の３つが考えられる。

・コミットする対象は時間を通して変化する要求の経路であり，その経路に従っている限り評判は保たれる。この場合，コミットメントは要求と受け入れ拒否の両面だが，要求が時間を通して変化している分だけ事前には自由度が上がっている（Kambe, 1998）。

・一定時間後には頑固なタイプも要求を変えられる。あるいは，頑固なタイプでも確率的には要求を変えられる機会がやってくる。この場合，機会は少ないが，要求を変えるチャンスがある。

・要求を変えることはできるが，その際に，要求を変えるコストが発生したり，あるいは，評判が低下する。この場合，要求は自由に変えられるとしても，直接あるいは間接のコストのため，それほど頻繁には要求を変えないことになる。

これらの状況を考えるといくつか関連した疑問が出てくる。一つには，変更できる可能性があるときにはどんな均衡が起こるかである。また，そのような可能性があることがプレイヤーにとって（頑固なタイプにとってあるいは事前の期待値の観点で）望ましいかということも重要な問いになる。これらは将来への研究課題である。

Q．途中で要求を変化させる経路にコミットすると交渉に有利か

最初の要求を選べる評判モデルでは，有利になることはない。というのは，交渉力に見合っ【91 頁】た要求をすることで，それ以上のどんな要求に対しても相手に自分の要求を受け入れさせることができるからである（Kambe, 1999）。交渉力に見合った要求は整合的だから，それ以上にお互いの利得を同時に上げることはできないのである。
　相手が特定の要求に執着するコミットメントタイプであるとき，要求を途中で引き下げることにコミットすることが有効になる（Kambe, 1998）。初期の高い要求は，最初の時点で相手が妥協したときの利得を高めるが，一方で，評判モデルでは高い要求は交渉力を下げてしまう。このトレードオフを回避するために，最初の要求は高くし，途中で要求を下げることが有効な戦術となる。

４．どうして非整合（incompatible）な要求がなされるか

この章では，最初の要求を選べるモデルを基に，どうやってプレイヤーが最初の要求を選ぶかを考える。
　消耗戦が始まるためには，最初の要求時において，非整合な要求が出される必要がある。しかし，なぜ非整合な要求をするのであろう。相手の要求と整合的な要求をすれば，少なくとも相手の要求から得られる利得が確保できる。そこで，非整合な要求をする以上は，これと同等の利得が確保できなくてはいけない。オリジナルモデルでは消耗戦が起こる状況では，自分の利得が自分の要求と独立となる。そこで，最初の要求を選べるとしたとき，消極的な理由として要求を非整合にしてもおかしくない。相手の要求を受け入れることの利得より低くなければ（混合戦略を含め）どんな要求でも均衡で可能である。
　では，評判モデルで最初の要求を選べるとしたときはどうか。Abreu and Gul（2000）の評判モデルでは，頑固タイプがコミットする要求には自然な分布があると想定されている。いいかえると，頑固タイプがする要求には自然な値があるという想定である。一般に頑固タイプは高い要求をすると想定されているので，非整合な要求がなされることになる。ただし，彼らのモデルの均衡では，一般にはどちらかのプレイヤーが相手の要求を交渉の開始時に正の確率で受け入れる。ここで，もしそのプレイヤーが要求をもう少し下げておけば，逆に相手に自分の要求を交渉の開始時に正の確率で受け入れさせられる。つまり，非整合な要求の下では，少なくとも一方のプレイヤーは非整合の度合いを下げたいというインセンティブを持っている。そこで，評判モデルで要求を自由に選べるようにすると，均衡では要求は整合的になる（Kambe, 1999）。
　以下では，要求を自由に選べる評判モデルで，どのような状況で非整合な要求が均衡で起こるか検討する。評判モデルでは非整合な要求は交渉が決着しない確率を生み出すので，相手の要求を受け入れるより厳密に大きい利得が得られなければ非整合な要求をすることはない。そのような要因があるとき，これを非整合な要求の積極的理由と呼ぼう。積極的理由がある状況としては２つの可能性が考えられる。一つは，あるプレイヤーに複数のタイプがあり，そのうちの一つのタイプに非整合になりやすい高い要求をする外生的な理由がある場合である。他のタイプは合理的に行動して中程度の要求を行うので，相手は後者の可能性に賭けて時には非整合になってしまう要求をしてくることがあり得る。もう一つの可能性は，その逆で，何らかの理由で非常に低い要求をするタイプがいる可能性がある場合である。相手のプレイヤーがこの可能性に賭けて高い要求をしてきた場合，このプレイヤーが合理的なタイプで中程度の要求を【92 頁】した場合には両者の要求は非整合になってしまう。いずれにせよ，ある種のタイプは他のタイプと利得の構造が異なっており，それが非整合な要求を起こす積極的理由となっている。

Q．最初の要求を選べる評判モデルで，要求に関して混合戦略が取られることがあるか

頑固なタイプの確率が小さければ，均衡でなされる要求はほとんど整合的になる。そこで混合戦略が起こるとしても，それぞれのプレイヤーの出す要求はほとんど変わらず，実質的には混合戦略の均衡ではない状況と近くなる。これを理解するために，Kambe（1999）で導入した交渉力に見合った要求を考える。その分析で示されたように，頑固なタイプの確率が小さければ，それぞれのプレイヤーはその値に近い値を自分に確保できる。そこで，どのプレイヤーもその値よりそれほど小さい値を要求することはなくなる。とすれば，相手もそれほど大きい値を要求することはしない。（最初の要求を選べる評判モデルでは，相手の一番高い要求は，こちらの最小の要求と整合的な値あるいはそれ以下になることを示せる。）そこで，頑固なタイプの確率が小さいときは，プレイヤーたちは交渉力に見合った要求に近い要求をする。交渉力に見合った要求は整合的であるので，上の主張が成り立つことになる。

Q．評判モデルで，不確実性があることでシグナリングとして不整合な要求がなされることがあるか

利得構造や確率構造に不確実性があり私的情報が存在するとき，この情報を伝えるために，高い要求をシグナルとして使うことが不整合な要求を引き起こすのではと推測する人がいるが，これは正しくない。それは，要求自体は利得に直接影響を与えない（payoff irrelevant）ため，いわゆるSCP（single crossing property）を満たさず，シグナルが利得に与える影響がタイプごとに異ならないからである。このため，要求自体がシグナルとして機能することはありえない（もしシグナルとして信じられればすべてのタイプがそのシグナルを送りたがる）。なお，シグナリングが起こらない状況で，利得に関連する変数（割引率や価値など）について不確実性がある場合，いったん消耗戦が始まれば，時間を通してソートされるように均衡のプレーが行われる。利得に関係しない変数，たとえば頑固タイプの確率，に関して不確実性があっても妥協の起こるスピードには影響を与えない。
　シグナリングが起こるとすれば，タイプごとに利得の構造が異なり，SCPを満たす変数がある必要がある。たとえば，妥協の価値か割引率のどちらかがタイプごとに異なり，ve^－ritがタイプごとに異なる場合を考えよう。この状況では，Admati and Perry（1987）のように要求をせずにただ待つ期間の長さがシグナルとなりえる。一方，頑固タイプの確率のように利得に関係しない変数は，どんな変数をとってきてもSCPを満たすようにはできないため，その情報をシグナルすることはできない。

Q．評判モデルで，両者に積極的理由がある状況はあるか？

交渉の開始にどんな要求でも受け入れるタイプ（以下ではチキンタイプと呼ぶ）がいる可能性がある状況を考えよう。このとき，高い要求をすることが利得を高める可能性がある。そこで，チキンタイプの可能性は，非整合的な要求をする積極的理由となる可能性がある。
　この状況では，以下のことがわかっている（Kambe, 2013b）。要求する際に，チキンタイプの可能性のないプレイヤーが先に要求を出し次にチキンタイプの可能性のあるプレイヤーが要【93 頁】求を出す場合には，チキンタイプの可能性がそれほど大きくなければ，要求は非整合とはならない。先に要求を出すプレイヤーが相手に付け込まれることを怖れるからである。これは，チキンタイプの可能性があるだけでは要求は必ずしも非整合にならないことを意味する。一方，チキンタイプの可能性のあるプレイヤーが先に要求を出す場合や，同時に要求する場合には，相手はチキンタイプに受け入れてもらうことを期待して高い要求を出してくる。これにより，要求は非整合になる。後者の状況では，次の性質が成り立つ。（i）こちらがチキンタイプである可能性に賭けて相手が高い要求をしてくる場合，相手にはチキンタイプの可能性がなくても，プレイヤーは自分の要求を多少高めた方がよくなる。つまり，自分がチキンタイプである可能性があることで，相手に加えて，自分も利得を高められる。（ii）プレイヤーが要求を高める度合いは，チキンタイプの確率に密接に関連し，その確率が低ければ，要求もそれほど非整合にならず利得の増加も小さい。評判モデルでは頑固タイプの確率が低くても影響が大きく出るが，それとは対照的である。

５．なぜ永久に続かないか

オリジナルモデルにおける混合戦略の均衡では，どんな長い期間をとっても，消耗戦がその期間内では終わらない可能性がある。しかし，現実的な交渉では，ほとんどの場合，一定の期間内に交渉が終わることが想定されている。無限に続く可能性があることに本質的に依存したモデルはその妥当性について慎重に検討すべきである。有限で終わるとすると，どう終わるかが交渉全体に影響してくる。終わりを見越してプレイヤーたちは妥協するかどうかを決めてくるからである。そこで，有限で終わる理由や有限で終わるときの均衡を考えることが意味を持ってくる。

Q．消耗戦の終わり方にはどんなものがあるか

理論的な観点からは，以下の３種類が考えられる：（１）両者がこれ以上交渉を続ける価値がないと合意したとき，（２）一方が交渉を打ちきり別な手段で解決してしまったとき，（３）外生的なデッドラインが来たとき^7）。これ以外の状況では，交渉を打ち切るより交渉を続けた方が利得が高く，合理的なプレイヤーが交渉を終わらせることは起こらない。もうこれ以上交渉は続けられないと言って相手の妥協を引き出そうとする戦術は，お互いに再交渉の可能性があることを知っている以上は意味をなさない。
　消耗戦が続くためには，相手の要求を受け入れる妥協の可能性がお互いにある必要がある。そこで，一方だけが消耗戦の途中で妥協を終了することはあり得ない。消耗戦のある時点で妥協の可能性がなくなるならば，デッドラインでの終了を含め，それは両方のプレイヤーで同時に起こらなくてはならない。

Q．どんな時に両者がこれ以上交渉を続ける価値がないと合意するか

消耗戦の終わり方として「両者がこれ以上交渉を続ける価値がないと合意」するという類型があるが，これは次の２つの状況でのみ起こる：（i）それぞれのプレイヤーに頑固なタイプの【94 頁】可能性があり，ある時間までに柔軟タイプは全て妥協して，その時間になると，両者はこれ以上誰も妥協しないと合意できるとき（評判モデル），（ii）プロジェクトのネット・ペイオフ（ベネフィットからコストを引いたもの）が下がってきてゼロになるとき。

Q．デッドラインでの終わり方にはどんなものがあるか

上でも議論したとおり，消耗戦が起こる均衡では，一方のプレイヤーが妥協する可能性があるときは，もう一方のプレイヤーについても妥協する可能性がある必要がある。このことを考慮すると，デッドラインでの終わり方は，以下の３種類に絞ることができる。

・特殊ケース　「同時に妥協したときの利得＝単独で妥協したときの利得」：消耗戦はデッドラインの直前まで続いて終了することが可能である。ただし，なぜこの等式が成立するかは不明。

・一般的なケースA（待ち時間が同じになる場合）「同時に妥協したときの利得＞単独で妥協したときの利得」：デッドライン間際に何もしない待ち時間が存在する。t ＝ S からt ＝T までは誰も妥協せずにただ待つ。デッドラインでの利得は，この待ち時間が両者でちょうど同じになるように調整されなければならない。

・一般的なケースB（待ち時間が同じにならない場合）この場合，均衡では消耗戦が起こらないことになる。ここでは，消耗戦が起こった場合に待ち時間が短くなる方が，交渉の最初に必ず妥協することになる。評判モデルのように妥協できない可能性のあるときではこの状況は起こらない。

Q．デッドラインでの利得を決定する要因は？

上記の一般的ケースAを実現するには，デッドラインでの利得をうまく設定しなければならない。そのような方法としてはどのようなものがあるか。一般に同時手番の混合戦略均衡であると，利得は一意に決まってしまう。これではうまく利得を調整できない。
　評判モデルでは，頑固なタイプが受け入れないので，最後の期に頑固タイプの条件付き確率が十分大きければ，妥協しない確率を大きい方向へ調整することが可能である。（小さい方への調整はできない。）そこで，どちらかのプレイヤーで最後の期に妥協しない確率を大きくすることで，利得に変化を与えられる。

６．最近の話題

交渉の途中で「交渉から降りる」と脅すことは，再交渉を考えると有効でない。しかし，別な相手と交渉するという脅しは，場合によっては有効になる。一般に，現在の交渉以外の機会を，アウトサイドオプションという。相手に一定の利得を保証するアウトサイドオプションがあるときは，それ以上の要求をしたら評判は使えない（Compte and Jehiel, 2002）。相手にとってアウトサイドオプションを受け入れる方が良い状況では，こちらが要求にコミットしても，相手には決して受け入れてもらえないからである。より興味深い状況は，交渉相手が２人以上いて，誰と交渉するかを選べる時である。この場合には，他の交渉相手に乗り換えるという脅しが意味を持つ。そこでの利得は，均衡の中で決まるという意味で内生的に決まる（Atakan and Ekmekci, 2009, Özyurt, 2010）。Özyurt（2010）は一人のプレイヤーが２人以上のプレイヤー【95 頁】と交渉するとき，評判はアウトサイドオプションを通して一人の側（shortside）の交渉力を強くすることを示している。

７．終わりに

本小論では，これまでの消耗戦の定式化について，現実妥当性の観点から検討してきた。その議論で明らかになってきたように，ある程度は，現実の交渉過程をうまく表していることが分かった。しかし，同時に，まだ現実の交渉の過程を取り込めていない点も示された。上記では議論できなかったが，実際の交渉では，ある要求にしばらく固執した後，少し譲歩した要求に切り替え，またその要求に固執するというように，多段階で消耗戦が起こることがあるが，この状況も現在の交渉理論ではうまく定式化できていない。これらのことは逆に，定式化で不十分なところをさらに吟味し代替的な定式化を考えることで，消耗戦のモデルを使った交渉の分析は今後も発展が見込めることを示唆する。さらなる研究が待たれるところである。

References

Abreu, Dilip and Faruk Gul（ 2000） “Bargaining and Reputation,” Econometrica, 68, 85-117.

Abreu, Dilip and Rajiv Sethi（2003）“Evolutionary Stability in a Reputational Model of Bargaining,” Games and Economic Behavior, 44, 195-216.

Admati, Anat R. and Motty Perry（1987）“Strategic Delay in Bargaining,” Review of Economics Studies, 54, 345-364.

Atakan, Alp E. and Mehmet Ekmekci（2009）“Bargaining and Reputation in Search Markets,”mimeo.

Bliss, Christopher and Barry J. Nalebuff（1984）“Dragon-slaying and Ballroom Dancing: The Private Supply of a Public Good,” Journal of Public Economics, 25, 1-12.

Compte, Olivier and Philippe Jehiel （2002）“On the Role of outside Options in Bargaining with Obstinate Parties,” Econometrica, 70, 1477-1517.

Crawford, Vincent P.（1982）“A Theory of Disagreement in Bargaining,” Econometrica, 50, 607-637.

Ellingsen, Tore and Topi Miettinen （2008）“Commitment and Conflict in Bilateral Bargaining,” American Economic Review, 98, 1629-35.

Fudenberg, Drew and Jean Tirole（1986）“A Theory of Exit in Duopoly,” Econometrica, 54, 943-960.

Ghemawat, Pankaj and Barry Nalebuff（1985）“Exit,” The RAND Journal of Economics, 16, 184-194.

Gul, Faruk, Hugo Sonnenschein and Robert Wilson（1986）“Foundations of Dynamic Monopoly and the Coase Conjecture,” Journal of Economic Theory, 39, 155-190.

Hendricks, Ken, Andrew Weiss, and Charles Wilson （1988）“The War of Attrition in Continuous Time with Complete Information,” International Economic Review, 29, 663-680.

Kambe, Shinsuke （1998）“Reputation and Incomplete Information in Bilateral Bargaining,” presented at the 1998 Japanese Economic Association Meeting.

Kambe, Shinsuke （1999）“Bargaining with Imperfect Commitment,” Games and Economic Behavior, 28, 217-237.

Kambe, Shinsuke（2013a）“The Commitment in Bargaining: not to Make a Lower Demand versus not to Accept a Lower Offer,” mimeo.

【96 頁】

Kambe, Shinsuke（2013b）“The Chicken Type and Incompatible Demands in Bargaining,” presented at the 2013 Japanese Economic Association Meeting.

Kennan, John and Robert Wilson （1989）“Strategic Bargaining Models and Interpretation of Strike Data,”Journal of Applied Econometrics, 4 Supplement, S87-S130.

Kornhauser, Lewis, Ariel Rubinstein and Charles Wilson（1989）“Reputation and Patience in the ‘War of Attrition’,” Economica, 56, 15-24.

Maynard Smith, John （1974）“The Theory of Games and the Evolution of Animal Conflicts,” Journal of Theoretical Biology, 47, 209-221.

Myerson, Roger （1991） Chapter 8, Game Theory: Analysis of Conflict, Cambridge, MA: Harvard University Press.

Ordover, Janusz A. and Ariel Rubinstein（1986）“A Sequential Concession Game with Asymmetric Information,”The Quarterly Journal of Economics, 101, 879-888.

Özyurt, Selçuk（2010）“Searching a bargain: power of strategic commitment,” mimeo.

Ponsati, Clara（1995）“The deadline effect: A theoretical note,” Economics Letters, 48, 281-285.

Ponsati, Clara and Jozsef Sakovics （1995）“The war of attrition with incomplete information,” Mathematical Social Sciences, 29, 239-254.

Rubinstein, Ariel（1982）“Perfect Equilibrium in a Bargaining Model,” Econometrica, 50, 97-110.