【49 頁】
共分散に関する多変量解析の可視化教材
白田由香利,高橋 裕
要旨
経済・経営分野における多変量解析において,分散共分散行列は重要な概念であり,それを真に理解させることは,経済・経営数学教育において非常に重要である。本稿では,分散共分散行列および,共分散を説明するために,その可視化を行う。共分散を使う多変量解析は多いが,そのなかでも,回帰分析および主成分分析は頻繁に使われる。そこで,この2種類の分析で共分散がどのように活用されるかを,標本サイズを次第に増加させながら視覚的に説明する2次元並びに3次元で可視化したインタフェイスを示す。また,時系列データの比較において,共分散が標準化された2系列データの類似度の尺度と解釈できることを示す教材を示す。
1.始めに
統計分野において多変量解析手法を教える場合,可視化は有効である。線型代数などの他の分野の数学に比較して,可視化が有効である理由として,「標本サイズを次第に増加させた際の変化のようすを見せることで,定理や解析アルゴリズムの数学的意味を理解できるようになる」ことがあると考える。近年コンピュータグラフィクスを用いた数学の可視化が多用されるようになり,数式の可視化は数学教育で大いに効果をなしている。しかし,シミュレーションと組み合わせた動きのある統計グラフィクス教材の研究は,発展途上にあると言えよう。
本稿では,古典的統計手法である回帰分析と主成分分析(PCA)を例にとり,分散,共分散の可視化を提示する。次節では,標本分散と不偏分散の違い,及び分散,共分散の概念を可視化する。第3節では,それを基に,単回帰分析のプロセスを可視化する。第4節では,2つの時系列データの比較において,共分散が標準化された2系列データの類似度の尺度と解釈できることを示す教材を示す。第5節では,単回帰分析と主成分分析の違いを明確にするための可視化を行う。第6節はまとめである。
2.不偏分散,分散,共分散
本節では,不偏分散,そして2変量の分散と共分散を可視化でどう見せるかを論じる。
まず,不偏分散を扱う。学生から頻繁に寄せられる,不偏分散に対する質問として「どうして標本サイズN ではなく,(N−1)で割るのか」がある。既存の統計の教科書では,「平均値
【50
頁】
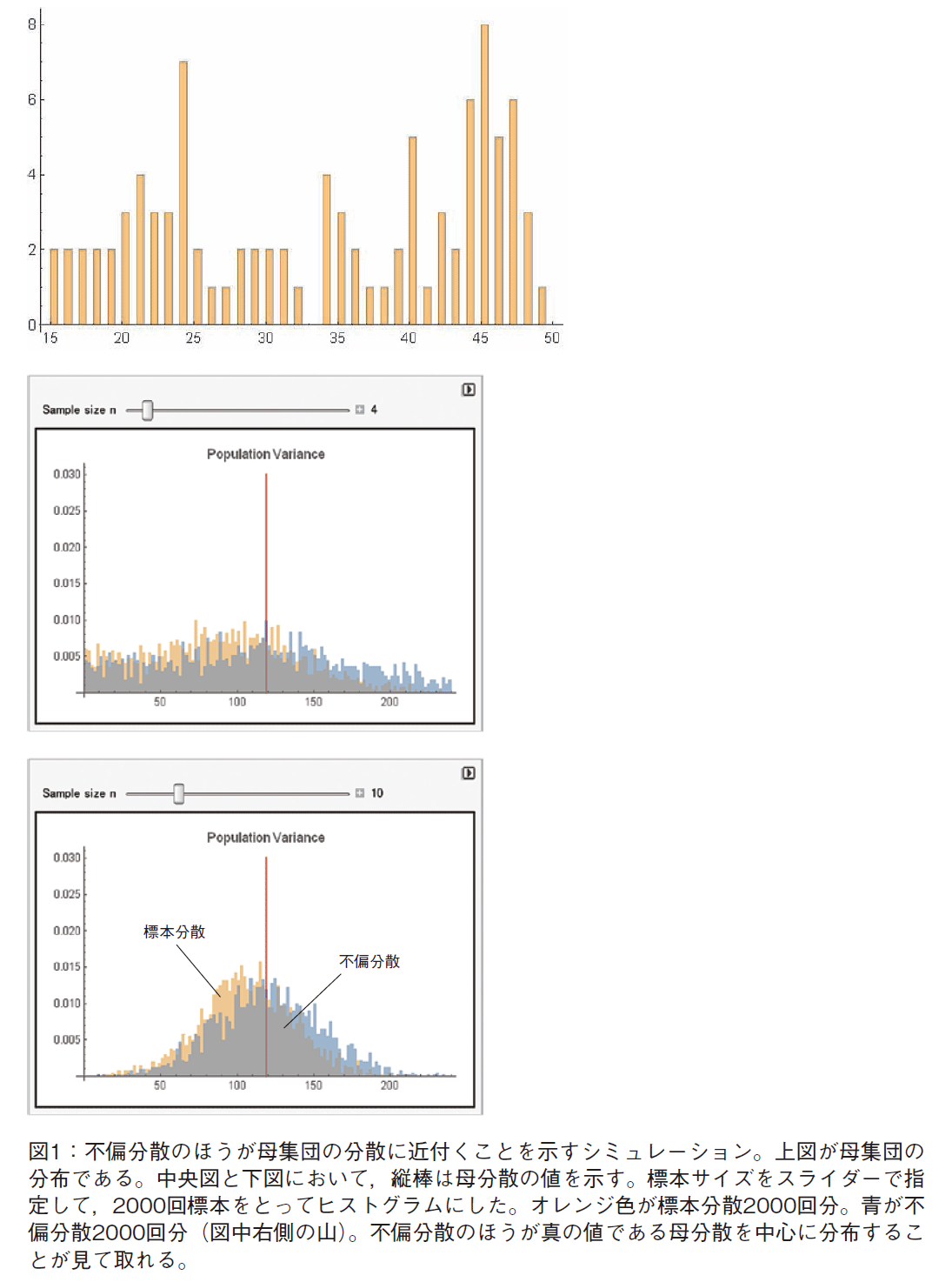
として標本平均を利用しているので,その分の散らばり度合いが小さくなるため,分母をNではなく(N−1)で割ることで,その分の補正をする」というように自由度に関する記述として説明している[1]。もちろん,この説明で十分理解する学生もいるが,図1のような動くグラフィクスを操作してみることで,「母集団の分散を中心に分布するのは,標本分散よりも不偏分散である」ということが視覚的に理解できる。
Web上で可視化例を画像検索などで検索すると,図1のような可視化例を検索できるが1)
,ポイントは,スライダーにより標本サイズを大きくするに従って,標本分散の分布と不偏分散の分布がどのように近づいてくるか,その変動のようすを見せる点である。これにより,両者の意味の違いを理解することが容易となる。
次に単回帰分析のような2変量を扱う際の分散,共分散を可視化について論じる。本稿では,2変量の標本データを,予め重心が原点になるように全体的に移動させる。後には,重心を移動する教材を使うが,始めは重心を原点に移動させたほうが,話のポイントが絞れるので,学生が共分散などの概念を理解しやすくなると考える。
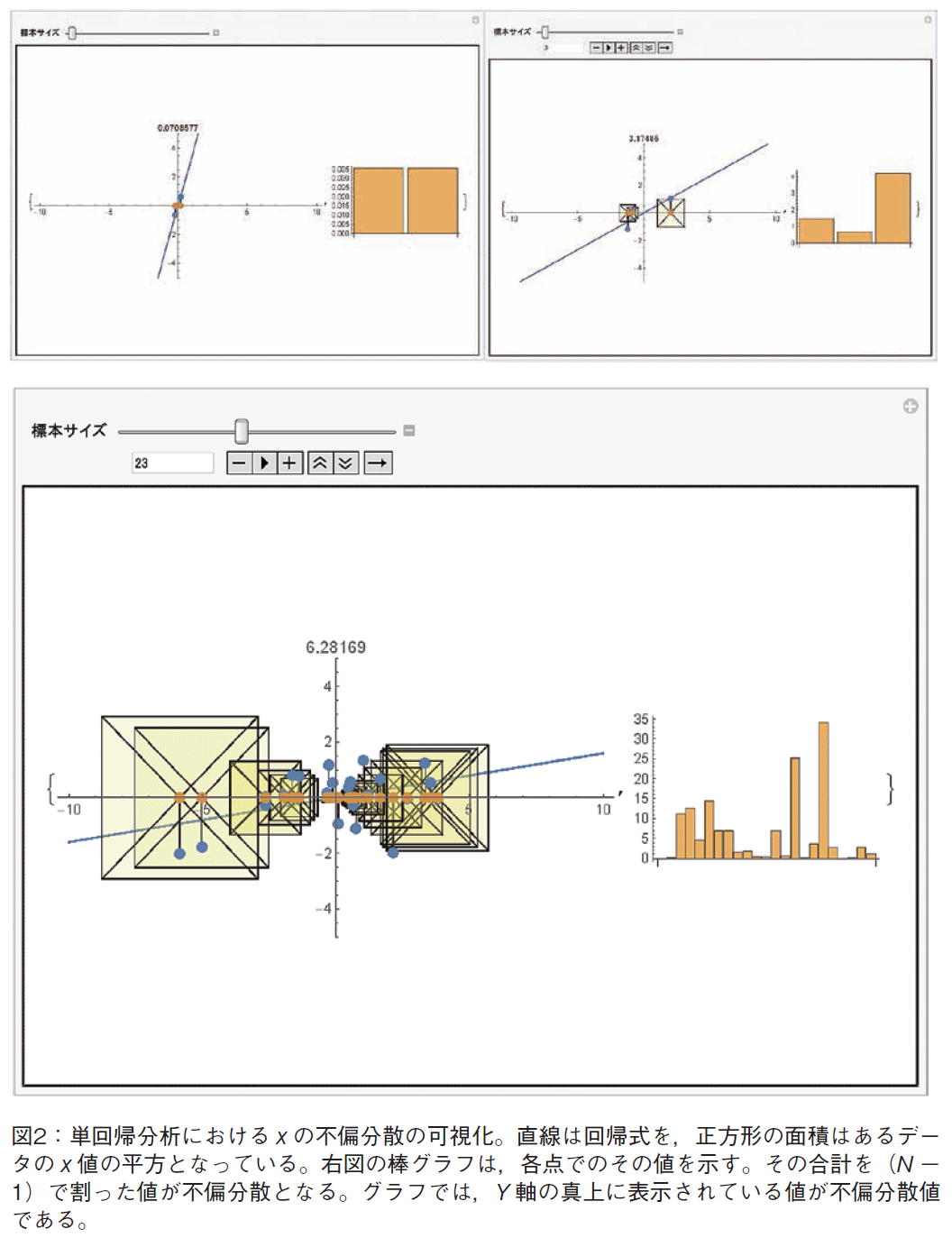
図2に,x の不偏分散が計算されるプロセスを可視化した。与えられた点(x,y )はx 軸上に投影され,その投影点を中心として,原点からの距離の2乗の面積をもつ正方形が描かれる。スライダーによって標本サイズを動かすことで,(1) 回帰式の傾きが変化すること,(2) 標本のx が0から離れるに従い,その距離の2乗が大きくなること,などが身をもって体感できる。
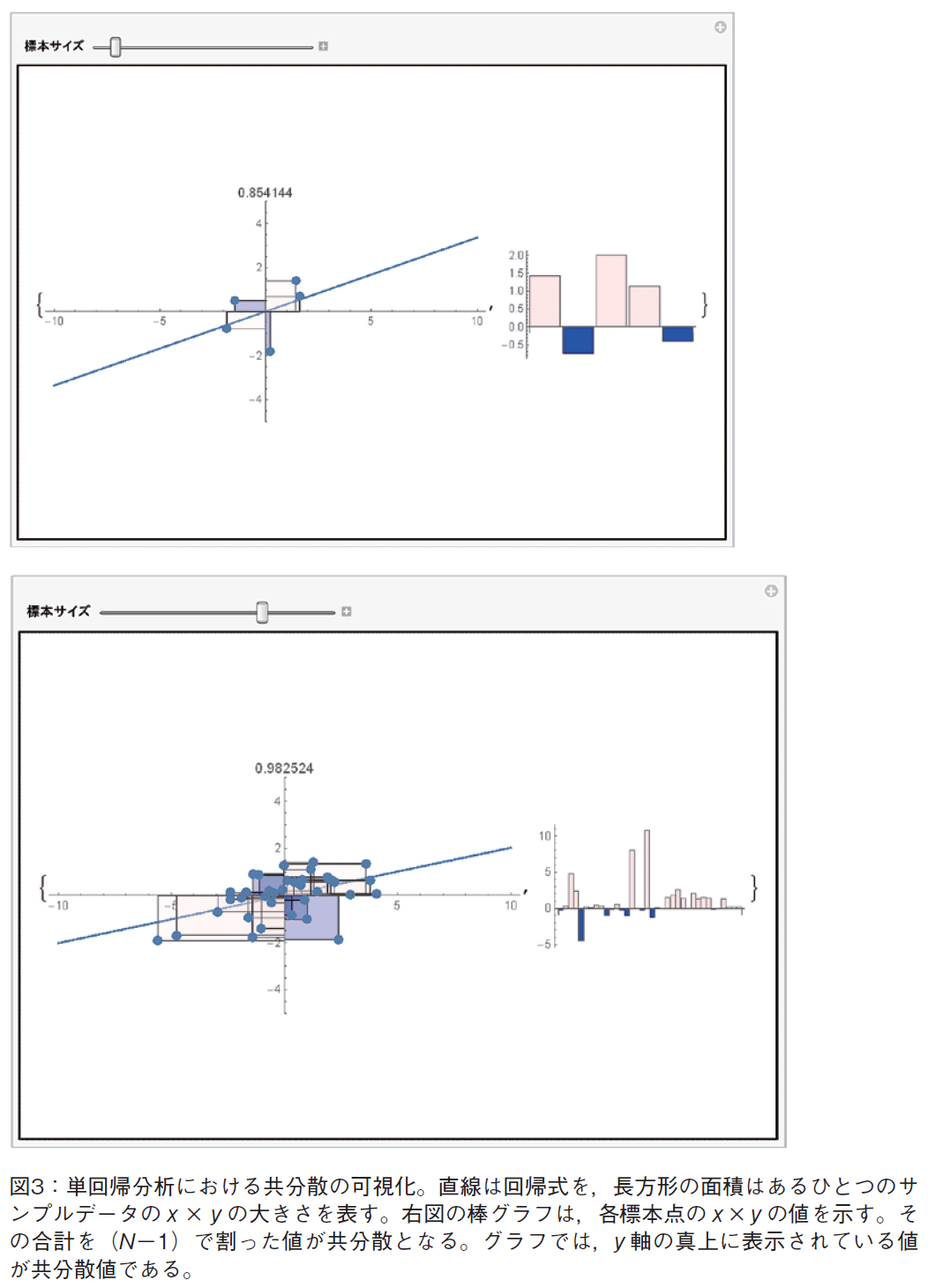
次に単回帰分析における共分散の可視化を行う(図3参照)。原点を中心として,2変量の正負の符号が同じであれば,x×y の値は正となり,符号が異なればx×y の値は負となる。図では,第1象限と第3象限に来た点が正の値となる。共分散とは,標本すべてのx×y の値の和を(N−1)で割った値であるので,第2象限と第4象限にデータが多い場合,値が負になることがグラフィクスから見て取れる。共分散の各項が半透明の長方形で示され,その長方形が重なって表示される。正負は色によって示されるので,相関の正負によって共分散がどのように変化するかが視覚的に理解できる。
【51 頁】
【52 頁】
【53 頁】
【54 頁】
【55 頁】
【56 頁】
【57 頁】
3.単回帰分析の可視化
本節では,単回帰分析の回帰方程式を求めるアルゴリズムの可視化を論じる。
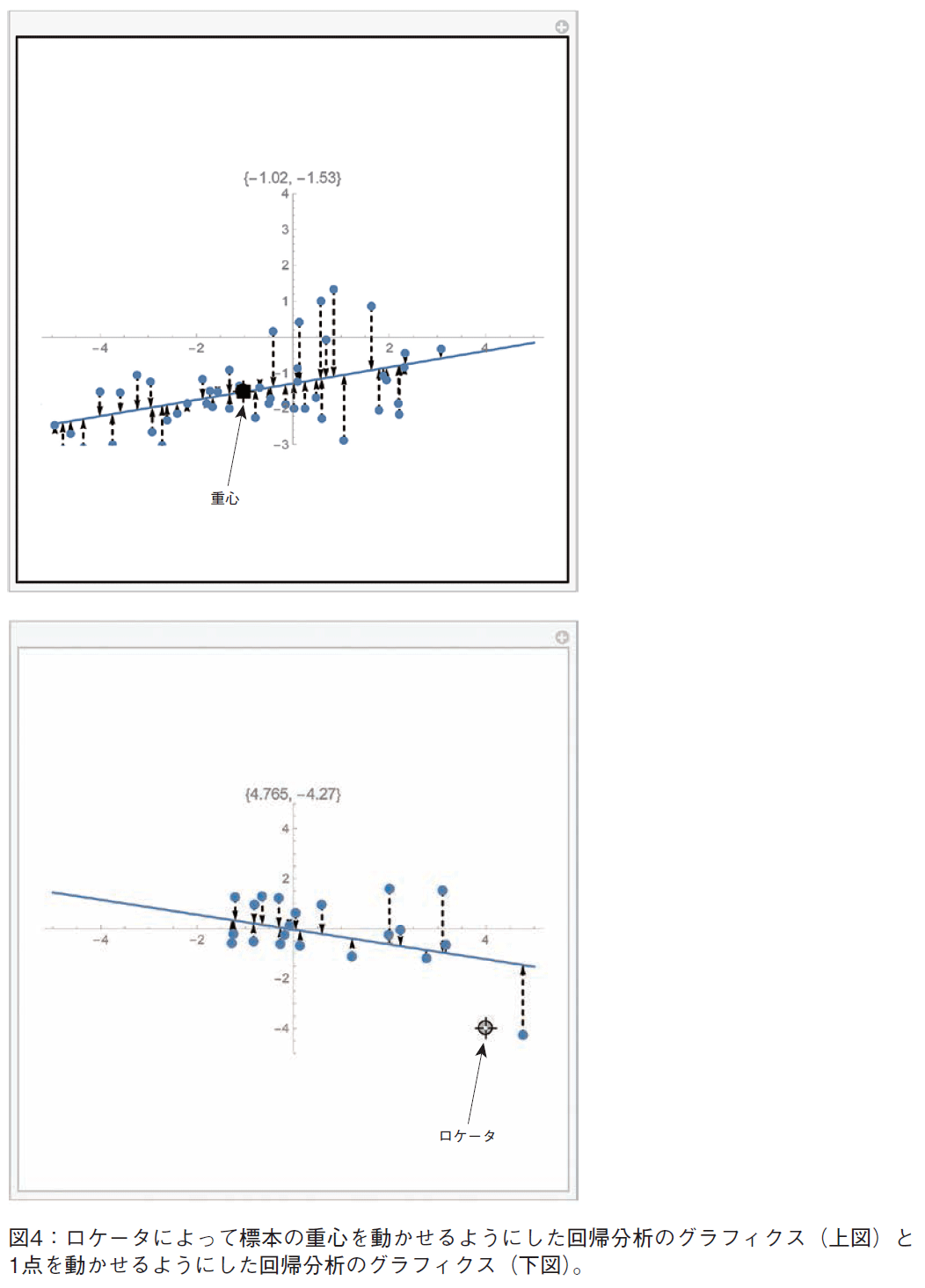
まず,回帰分析になじんでもらうため,図4に示すような,ロケータを使った回帰分析の教材を提示する。ロケータは対話的に点を移動させることができる機能である。図4上図は,重心位置をロケータで対話的に移動させる教材である。図4下図は,標本データの一つをロケータで動かすことで,回帰直線の移動するようすを感じてもらう教材である。
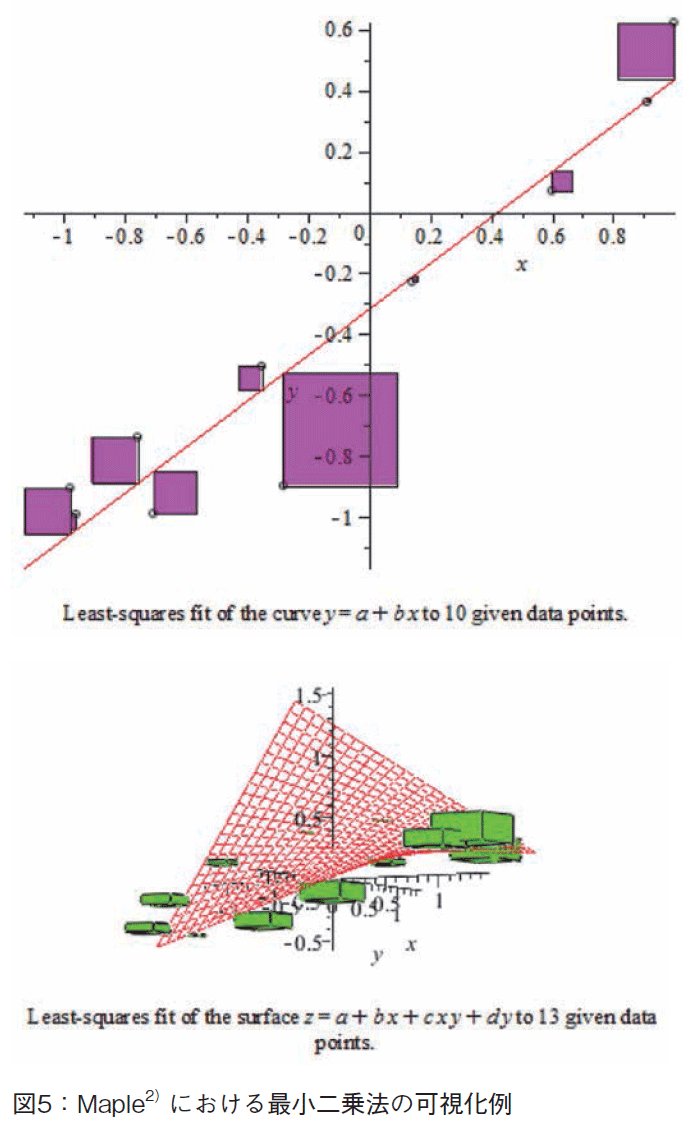
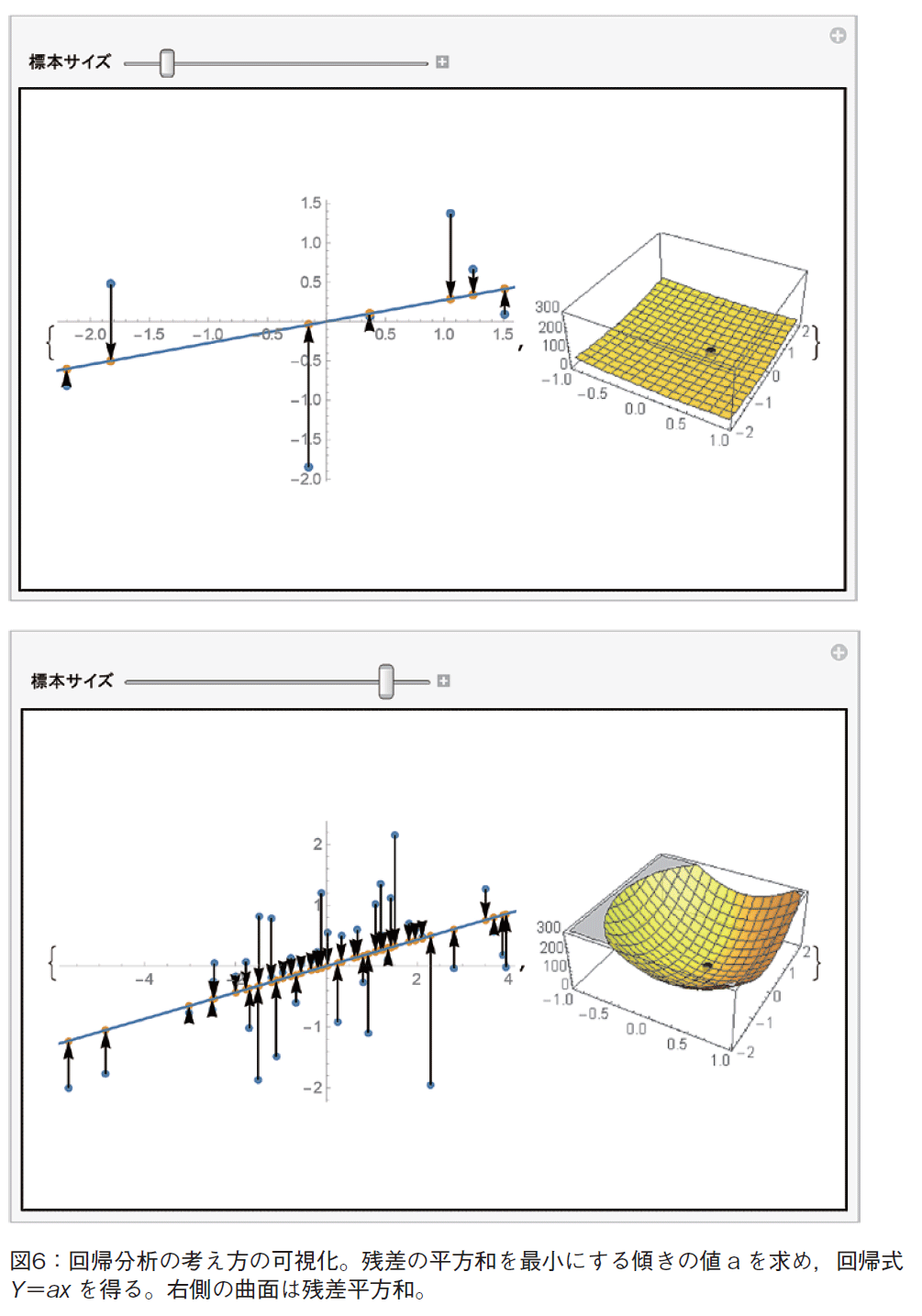
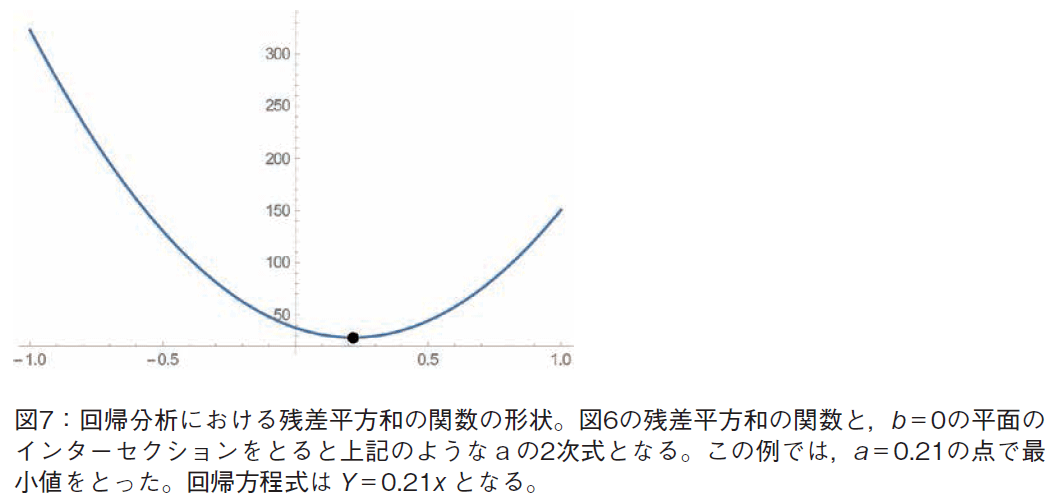
回帰分析は,残差の平方和を最小にする点を求めるため,最小2乗法を用いている。最小2乗法の可視化としてMaple のように,残差の平方の値を面積とする正方形等で示すという方策がある(図5参照)。我々は,今回の回帰分析の可視化では,残差をベクトルで表し,残差平方和の作る3次元曲面を示した(図6参照)。回帰方程式を Y=ax+b とおく。標本データの重心を予め原点に移動させておくので,b は0である。残差平方和は,2変数a,b の関数となる。図6では,標本数が増加するに従い,この3次元曲面の尖度が増加するようすが見て取れる。図7は,b=0の平面とこの曲面のインターセクションの2次元グラフである。最小点の値が読み取れる。ロケータでフィッティングする傾きを自分で変化させながら,その点(a,b)における残差平方和が最小に近付く様子を,手を動かして実感する,という点がポイントとなる。
以下では分散共分散行列に関する可視化について論じる。分散共分散行列は次のように表わすとする。
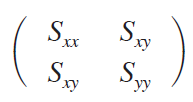
分散共分散行列から直接回帰式の傾きを求める公式は,a=Sxy / Sxx であるが[2],これを学生に理解させるために,上述した不偏分散と共分散の可視化(図2,図3)を使うと効果がある。次元でみると,Sxx(不偏分散値)でSxy(共分散)を割っているのだから,その比が傾きであることは自然に理解される。また,図3において,第2象限及び第4象限にデータが多い場合,
【58
頁】
分散値が小さくなり,回帰式の傾きが小さくなるようすを見せると理解がよい。
講義では,可視化によりa=Sxy / Sxx を理解させたあとで,代数的計算を自分でやらせている。標本数は3程度が適当と考える。方法は,残差平方和の式を,a について偏微分して0とおき,その式をa について解く。式の変形が苦手な学生には,始めに数学ツールで答えを見せて,その後自分で解かせるとよい。図8にMathematica3)
を用いて,計算したようすを示す。ここで,D[expr, a]は偏微分を表す。Coefficien[t expr, a]は,式 expr の中で変数 a の係数を求める関数である。Simplify[expr]は式の簡素化を行う。
同様に,重回帰分析における公式の導出の際も数学ツールを用いると,式の変形が苦手な学生の支援となる。図9は,回帰式を Y=a1×x1+a2×x2+b とした際のMathematica による数式処理を示した。結果として,以下の方程式が得られ,この方程式を解くことでa1,a2 が求められることが分かる[2]。
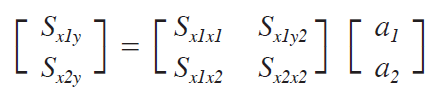
統計において,公式は行列表記などで簡単な式で書けるが,その式の意味を理解するためには,可視化と代数の計算の両面からの指導が必要と考える。そして,昨今の機械学習における統計処理のような複雑な計算は,少ない次数であっても計算が難しい場合が多い。その際,全体の動きを可視化でとらえ,数式処理ツールなどを使って式の変形を確認しながら,理解していくことは,式の理解に必要と考える。

【59 頁】

4.時系列データの類似度
本節では,共分散の応用として,2つの時系列データの類似度について論じる。2変数の相関係数は,データを標準化した場合,2変数の共分散
2変数x,y を2系列の時系列データと見る。図10左図に2系列データ例を示した。2つのデータ系列の距離の和が小さいほど,類似度は高いと解釈できる。それは上式の左辺の距離が大きくなり,右辺の共分散が小さくなることに対応する。
【61
頁】
【62
頁】
5.主成分分析との比較
本節では,2次元の標本データの主成分分析の可視化を行う。
6.まとめ
2次元標本データの回帰分析と主成分分析を使い,分散及び共分散の意味を理解する可視化を行った。こうした統計における可視化は,従来から広く行われてきたが,本稿の可視化ポイントは,標本データサイズを動かすことで分析結果が変わってくるようすを理解する点にある。著者の作成したスライダー付き統計グラフィクス教材として,中心極限定理を説明するものなどがある[14,15]。
謝辞
本論文の作成にあたり,常日頃から有意義な助言を頂いております学習院大学経済学部 森田道也教授,田中伸英教授,学習院大学計算機センター久保山哲二教授に感謝します。
参考文献
1. 涌井良幸,統計解析がわかった! 。2008:日本実業出版社。
2. 奥喜正,高橋裕,データ解析の実際─多次元尺度法・因子分析・回帰分析 2013:丸善プラネット。
3. 奥瀬喜之,久保山哲二,経済・経営・商学のための実践データ分析─アンケート・購買履歴データをいかす。2012:講談社。
4.Wonnacott, T. H. and R. J. Wonnacott, REGRESSION. 1981: John Wiley & Sons, Inc.
5.Konishi, S., Introduction to Multivariate Analysis: Linear and Nonlinear Modeling. Statistical Science.
【63
頁】
2014: Chapman & Hall/CRC.
6. Koch, I., Analysis of Multivariate and High-Dimensional Data. Cambridge Series in Statistical and Probabilistic Mathematics. 2013: Cambridge University Press.
7. Hastie, T., R. Tibshirani, and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition. 2 ed. Springer Series in Statistics. 2009 Springer.
8. 涌井良幸,涌井貞美,ピタリとわかる多変量解析入門。2008:誠文堂新光社。
9. 白田由香利,主成分分析のビジュアルな教授法。学習院大学計算機センター年報,2010. 31:p.63-73。
10.白田由香利,悩める学生のための経済経営数学入門。2009:共立出版。
11.Hashimoto, T. and Y. Shirota. Web publication of visual teaching materials for business mathematics. in Uncertainty Reasoning and Knowledge Engineering(URKE), 2012 2nd International Conference on. 2012.
12.Shirota, Y. and T. Hashimoto, Web Publication of Three-Dimensional Animation Materials for Business Mathematics: 10 Graphics for Economics Mathematics (Part 2). Annual Report of Gakushuin University Research Institute for Economics and Management(GEM Bulletin), 2012(26): p.13-22.
13.Shirota, Y., Practical Teaching Methods of Linear Algebra for Students in the Economics Course. Gakushuin Economics Papers, 2014. 51(2): p.133-147.
14.Shirota, Y. and S. Suzuki, Visualization of the Central Limit Theorem and 95 Percent Confidence Intervals. Gakushuin Economics Papers, 2014. 50(4): p.125-136.
15.Shirota, Y. and T. Hashimoto, Knowledge Visualization of Reasoning for Statistical Problems. Annual Report of Gakushuin University Research Institute for Economics and Management (GEM Bulletin), 2014. 28: p.45-54.
![]() となる。この場合,相関係数は共分散そのものとなる。一般に,相関係数は,標準化された2つのデータの類似度を示す尺度と解釈できる[3]。標準化された2系列データの共分散の式を変形すると以下を得る。
となる。この場合,相関係数は共分散そのものとなる。一般に,相関係数は,標準化された2つのデータの類似度を示す尺度と解釈できる[3]。標準化された2系列データの共分散の式を変形すると以下を得る。
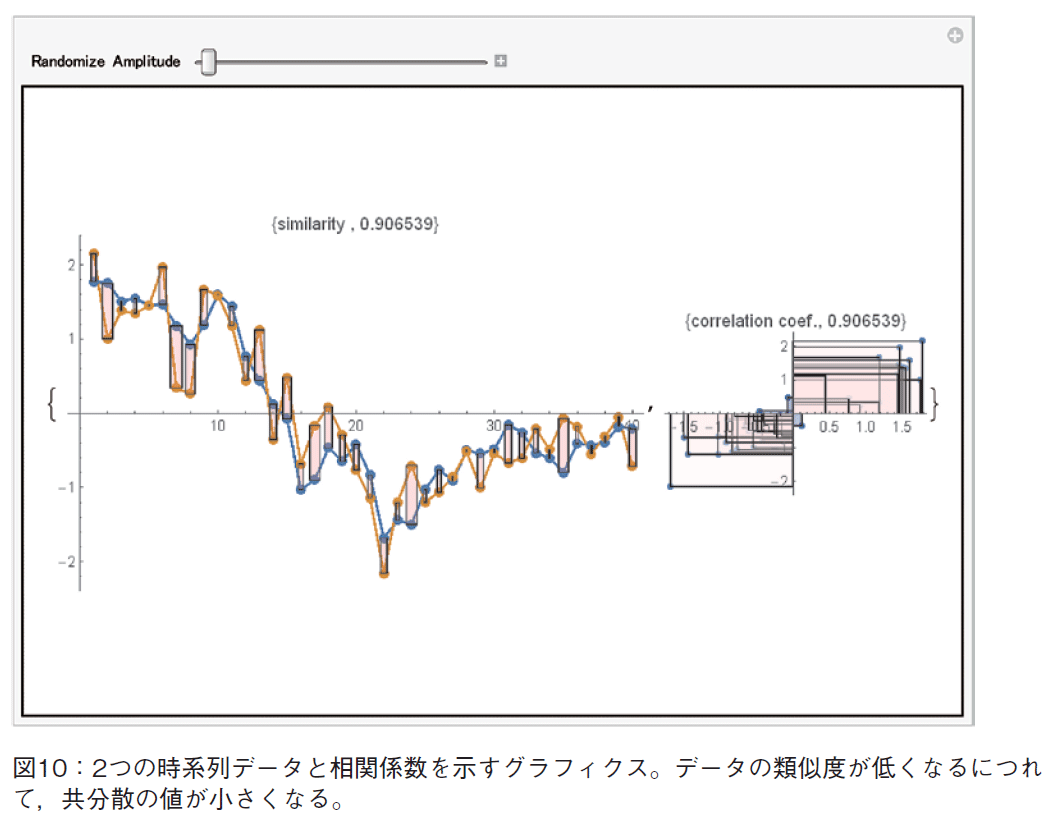
これを可視化した教材を図10に示す4)。グラフィクスで左図は,ある時点の2系列のデータの
【60
頁】
距離の2乗を面積とする正方形を描いている。画面上,縮尺の関係から長方形に見える。図10右図は,データ系列1を横軸に,データ系列2を縦軸にとり,共分散の項とともにプロットした散布図である。図4の共分散可視化と同様に,正負を色によって区別している。左図の距離の2乗の和が大きくなるに従い,右図の共分散の負の項が大きくなることが視覚的に理解できる。
本グラフィクスでは,データ系列1として,実際の株価データを使っている。そして,それに類似したデータ系列2は人工的に乱数により生成している。データ系列1に,正規分布N (0, var)に従う値を乱数発生させ変動分として加算して,データ系列2のデータを作成している。スライダーは,この分散varを変動させている。分散を大きくしたほうが,類似度は低くなる。分散varを大きくするに従い,距離の平方和が大きくなり,共分散は小さくなる傾向が見て取れる。その変動のようすを実感するためのグラフィクス教材である。
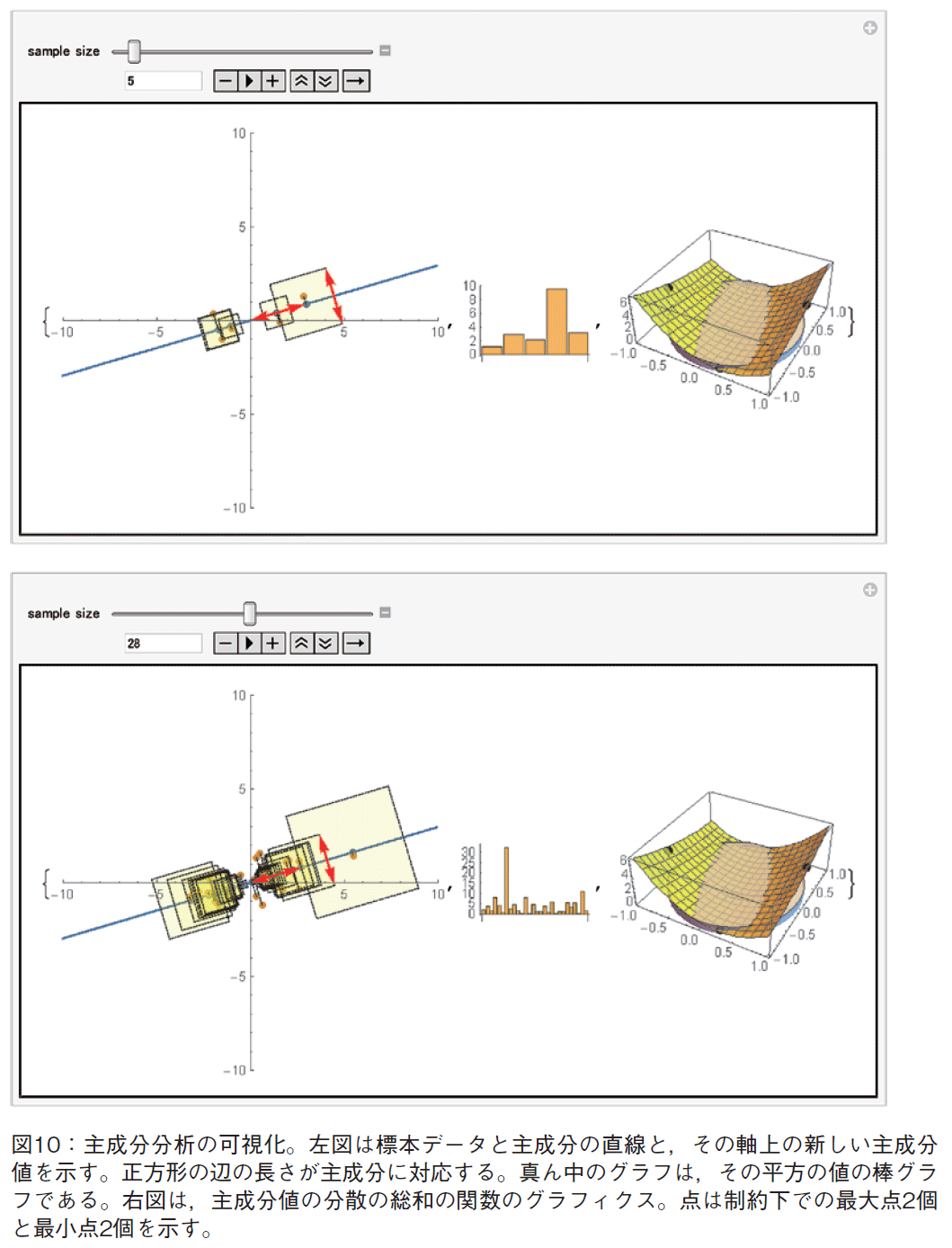
主成分分析は,主成分値の分散の合計が最大となる傾きを求める問題であり,標本データの分散共分散行列の固有値,固有ベクトル問題に帰着する[4-7]。可視化としては,主成分軸を標本データの見晴しがよくなるように取る[8]が,こうしたグラフィクスは2次元3次元標本データに対して,久保山などにより実装されている[3,9-13]。これらは,主成分軸を動かすことで,分散最大となる方向を探す,という目的のグラフィクスである。本稿で提案する主成分分析可視化グラフィクス(図9)は,回帰分析との違いを明確化することを目的とした。正方形の辺の長さが主成分に対応することが学生に分かり易いように,特定のデータに限り,両辺矢印で主成分及び正方形の1辺をハイライトし,残差と,主成分値の違いがグラフィクス上で明確になることを目指した。
特に共分散は,従来,あまり可視化が行われていなかったように感じる。しかし,今回の共分散の可視化によって,第2象限及び第4象限の負の値をとるデータの増加によって,その値が負になるようすが可視化できた。また,単回帰分析において,代表値である分散と共分散の比
が回帰式の傾きである,ということが視覚的に分かるようになった。
統計のグラフィクス教材は,標本データを増加させることで,得られる分析結果がどのように変化するかを動的に見せることが重要であると考える。今後とも,動的な統計のグラフィクス教材を作成していく所存である。