新しいページ 1

【65頁】

市場の厚みの分析～Depthの研究展望とHFT解明に向けての考察～

辰巳　憲一^*

１　はじめに

市場の厚み（デプス，Depth）とは，最良気配から上下何本かの気配値のもとで出された指値注文の数量列である。普通，単に厚みという場合，その分布ではなく，売り呼値（ask）と買い呼値（bid）の両側の和がとられる。しかも，何も記述がなければ最良気配のもとでの注文株数である。いずれにしても市場における流動性の指標の１つとされている。
　本稿は，DepthならびにDepthの分布を計量分析している2000年以降公表された先行研究を紹介し考察する。考察の対象は主として株式市場であるが，それ以外のディラー市場でのDepthでも，いくつか先行研究があるので紹介し参考とする。また，研究対象はティック・データや日次や月次のデータであるが，必ずしもHFT（高頻度取引）ではない。HFTにおけるDepth研究は，筆者が見るところ米国などでは深刻な理由があって，多くない。辰巳［2015］でも多少理論的に考察しているが，以下ではこの点も考察する。
　世界の主要国において，取引所で取引する際に，注文を非表示あるいは非公開にすることができる。これは呼値刻み，値決め方法，などと同様の，注文と執行方法の多様化であり，市場の魅力を高めているという捉え方がある。他方で，これは市場を見えなくしており，市場参加者の信頼を損なうという捉え方もある。非表示注文の実態はすべてが明らかになっているとは言えないが，Depthと市場へ与える影響は極めて大きい。この点を斟酌しながら考察する必要があることに注意しよう。

２　市場の厚みの分析例─先行研究の展望

２－１　前提知識

（１）呼び値の刻みと市場の厚み

米国では，過去数十年の間に，呼値刻みが，１/８ドルから６セント（≒１/16ドル）へ変更され，その後１/16ドルから１/100ドル（十進化）へと２度変更された歴史がある。その結果，【66 頁】呼び値刻み自体そしてその変更が市場にどのような影響を与えるか，与えたか，に対して関心が強かった。
　各呼び値のもとでの指値注文量を単純に足し上げただけのDepthは，情報を集計しているため，ある程度情報量を欠落させている。それゆえ，Depthの分布という概念は，あるタイプの有意義な情報を提供するものと予想される。
　例えば，投資家による指値変更のプロセスとその効果を記述するには，Depthの大きさだけでなく，Depthの分布が重要になってくる。約定価格の水準とそれが変化するプロセスにも，Depthの分布は何らかの形で影響する。
　気配値をDepthの分布で加重した平均も，市場参加者が行う指値の変化を敏感に反映する指標^1）として分析に用いられている。その最も簡単な平均は最良売り指値と最良買い指値の単純平均であるmid-quoteである。約定価格あるいは取引価格は，両側の最良気配値の間を変動しながら推移するバウンスがあるためボラティリティを大きくしてしまう。そのため，約定価格に代えて利用されることが多く，マーケット・マイクロストラクチャーの実証分析では，主流になっている。

（２）情報の公開

多くの国で2000年代前半以降，約定価格前後の気配値（例えば，３本値）とそれぞれの指値注文残高（Depth）が公開されるようになった。また，その数年後に例えば５本値，さらに10本値まで拡大するなど公開情報を増やしている^2）。
　公開する情報量を監督当局が増加させる場合，市場の質（質とは一体何であるのか議論はあるが，ふつうスプレッド等の流動性などが高いことを指す）^3）が改善するという研究とむしろ【67 頁】悪化するという研究の両方があり，論争の的である。
　様々な注文情報を市場参加者がどう捉えるかについては，いくつかの局面が考えられる。自身の情報が公開されてしまうとディーリングや投資に不利であるという局面がまず考えられる。他方，他の市場参加者が誤解するように情報を作為的に出す行為によって，他の市場参加者を欺き，自身を有利にするという行動も考えられる。後者の行動は公開情報の拡大でメリットを得ることができる。相反する，これら２つの要素のどちらが強いかによって，情報公開の捉え方は違ってくる。
　気配情報の価値という観点では，約定価格形成に果たす役割はもっとも重要であろう。この論点に関しても多数の研究がなされている。

（３）インデックス間などの比較にあたって

Angel-Harris-Spatt［2011］は，Knight Capital Groupのデータに基づき，流動性の指標とされる市場の厚みをS&P500銘柄，Russell2000とNYSE全銘柄で比較し，2003年12月以降2009年１月までの推移を確認する。全米最良気配（NBBO）に何株の注文が板上に出ているか，そして，最良気配から上下６セント（≒１/16ドル）まで離れたところに何株の注文が板上に出ているかの２つの指標でみると，前者の観点ではS&P500銘柄，NYSE全銘柄，Russell2000の順で大きい。しかしながら，後者の観点では，Russell2000とNYSE全銘柄の差は大きくなく，ともにダントツの大きさであるS&P500銘柄に続いた。
　時系列でみると，流動性の高いS&P500銘柄については，市場の厚みが顕著に増大している一方，流動性がそれほど高くないRussell2000は微増にとどまる。
　Angel-Harris-Spatt［2011］は，これらの現象をもって，HFTが高流動性銘柄あるいは市場に限って活動しているという仮説を検証するものであると考えたい，のであろう。
　Depthを規模の違う市場間あるいは時系列で比較するには，絶対値ではなく，相対化あるいは標準化して比較するしかない。銘柄間で比較する場合は，流動性などに大きな銘柄格差が存在し，更に注意しなければならないだろう。最近は，該当サンプル期間で平均した取引規模（trade size）や出来高で割る方法がとられることが多い。また，何らかの方法で，平均と標準偏差を計算して，正規化する方法も，とられる。
　しかしながら，Angel-Harris-Spatt［2011］はこのような方法をとっていない（とっているという説明は無い）だけでなく，後述する非表示注文についても，どれだけ，どのように適切に考慮されているかも不明であり，上の計測結果の信頼度は特に高くないと言わざるをえない，だろう。

（４）株式売買単位とDepth

日本では，発行企業が自社株式の市場取引を活発にするために，企業自身で株式売買単位を選択できる制度がとられている。このため，株式売買単位はいくつかの経済要因に依存して決められる（内生）変数になっている。
　しかしながら，例えば，イタリアでは2002年から，すべての企業について一律に１ユーロに変更された。その変化は，むしろ外生的なもので，投資家にとって与件になる。Perotti-Rindi-Fredella［2012］は，その効果を分析し，スプレッドの減少とDepthの増加が導かれたことを【68 頁】検出している。
　東証がそうであるように，株式売買単位や呼び値の刻み幅は，共に，株価水準とほぼ比例して設定されていることが観察されている。この点は，計測上様々な問題を引き起こす恐れがある。しかしながら，Perotti-Rindi-Fredella［2012］には，そのような考察はない。

２－２　Depthの決定因計測

２－２－１　呼び値刻み細分化前後の２期間クロスセクション分析

Chung-Charoenwong-Ding［2004］は米国の呼び値刻み幅の細分化，いわゆる十進化（decimalization）の効果を分析する。米国の呼び値十進化（１/16ドルから１/100ドルへの変更）は，呼び値刻みの微細化と非端数化という２つの局面がある。そして，先立つこと３度のパイロット導入を経て，2001年１月29日に制度導入は完了する。
　サンプルには，ニューヨーク証取のTrade and Quote（TAQ）データベースに基づく普通株2,629が選ばれ，十進化前後のそれぞれ30日が分析された。
　これらサンプルから，株価変化が十進化以前の時期に$１/16以下である19銘柄，十進化前後のいずれかで十分な数のサンプルがない銘柄，スプレッドが$５以上の銘柄，が除外され，最終的なサンプル数は2,603になっている。

（１）計測方法，結果と特徴

Chung-Charoenwong-Ding［2004］の計測方法は個別銘柄毎に，データの30日平均をとった，クロスセクションOLSである。銘柄は十進化前のスプレッドの大きさに応じてほぼ等分になる10グループに分け，計測される。自由度調整済決定係数は，クロスセクション分析としては十分高く，主要な回帰式では0.385を得ている。
　被説明変数は，十進化前後のDepth変化率（少数点表示）である。ただし，Depthは売買両側をたした株数にmid-quoteを乗じた金額表示（dollar depth）である。
　説明変数は，大きく分けて３つのグループに分けられる。株価，取引回数（the number of trades），取引規模（trade size），ボラティリティ（日次リターンの標準偏差），株式時価総額，の５変数それぞれの自然対数値の十進化前後の変化，が第一のグループである。
　いずれの変数も有意で，ボラティリティ以外の係数値の符号はプラスであった。最もｔ値が高いのは取引規模である（なお，被説明変数をスプレッドの変化率に変更した場合には，取引頻度を表す取引回数のｔ値が高い）。
　第二のグループは次の３変数である。これらの変数は，著者たちがもっとも注目する説明変数であるので詳しく説明しよう。
　１ティックの最小価格変化に相当するスプレッドが十進化前期間において（全体に）占める比率（論文での記号はPQMIN）。これは，マイナスで有意であった。もっと刻みの細かい値で指値注文したいにもかかわらず，仕方なく１/16単位で注文している，との考えで，この変数は呼び値刻みの粗さが取引を制約している確率を測っている，ものとみなされた。
　$１/16の奇数倍の気配（odd sixteenth quotes）の比率（論文での記号はPODD）。これは，有意でなかった。端数の呼び値は，市場参加者に嫌われ，注文が少なくなる。注文が少ない呼び値に対しては，時間優先や価格優先のルールの下では，執行される確率が高くなり，有利になる。本来はこのような効果を計測するためであった。
　十進化前のDepth自体の大きさが十進化によって何らかの影響を受けたかどうかを分析する【69 頁】ために，説明変数として，Depthが導入された。しかしながら，Depthは有意でなかった。
　そして，第三のグループが次の３つのダミー変数である。2000年８月28日からパイロット導入された７銘柄にダミー変数１，2000年９月25日からの57銘柄にダミー変数２，2000年12月４日からの94銘柄にダミー変数３，が付けられた（該当銘柄は１，その他０）。
　制度先行導入の銘柄は，後続する銘柄に影響を及ぼしていることが，予想される。しかしながら，Depthに対して，これらのダミー変数はいずれも有意ではなかった（なお，スプレッドが被説明変数になった場合には第二のダミー変数２だけが有意であった）。
　著者達が得た結論を要約すると，Depthは株価上昇（株価水準の高さではない）や取引の増加と比例し，ボラティリティと反比例し，呼び値の粗さに反比例する，ということである。パイロット導入の仕組みはDepthに影響しなかった。

（２）欠点や疑問点

説明変数の第一のグループは，類似の変数が多く，多重共線性問題などの問題を引き起こす恐れがあるにも係らず，計測上特別な配慮がなされていない。
　変化率と自然対数値差という，２つの類似する，変化を現す変数が混在している理由が述べられていない。
　米国の呼び値十進化の効果を分析したChung-Charoenwong-Ding ［2004］は，呼び値刻みの微細化と非端数化という２つの効果が混合した分析であり，それらを明瞭に分離しない限り，日本へは応用できない。

２－２－２　呼び値刻みが株価水準で変わる市場での効果分析

東証と同じように，呼び値刻みが株価水準で変わるクアラルンプール証券取引所（KLSE）の時系列分析をおこなったのが，Chung［2005］である。
　Chung ［2005］の研究では，1996年から2001年のクアラルンプール証券取引所上場銘柄の月次データが分析に用いられ，単純回帰分析でのサンプル数は３万超である。
　Depthはask側とbid側それぞれの和で千株単位の株数で定義され，被説明変数はその自然対数値 log（Depth）である。そして，説明変数は次の４つの変数と３種のダミー変数である。まず，最初の２説明変数は，株価の逆数（株価はaskとbidの中位値：計測結果はプラスで有意），log（出来高）（Trading volume：同プラスで有意），である。以上のすべての変数は日次データの月間平均である。
　次に，回転率（Turnover rate：月間平均日次出来高を月間出来高で割る：同プラスで有意），ボラティリティ（Return volatility：日次リターンの月間標準偏差：同マイナスで有意），の２変数が説明変数になっている。そして，ダミー変数は呼び値ダミー（高株価レンジで有意，しかしながら，符号は正負が混ざるので，含意は大変曖昧になる），銘柄ダミー，月ダミーの３種である。他に，定数項（有意）が加わる。

（１）特徴

この研究は，呼び値は７通り，銘柄数は812，月数は12なので，ダミー変数が極めて多い時系列クロスセクション計測である。呼び値刻みの効果をダミー変数で捉えようとする，呼び値ダミー変数法が特徴的である。呼び値ダミー変数の係数値を推定することが計測目的になっており，他はコントロール変数であるという取り扱いである。
　株価の逆数が説明変数になるのは，Harris［1994］以来の工夫を採用した結果であり，株価と関連する変数との多重共線性を避けるため，である。しかしながら，そう主張されるにも関【70 頁】わらず，気になる相関係数値は掲載されていない。
　スプレッドを被説明変数とする計測式も，決定因は同じという想定で，同じ回帰式スペックが用いられる。当然，回帰係数に期待される符号は違う。

（２）計測結果

自由度修正済み決定係数値は高く，主要変数は有意であった。Depthは，株価水準とボラティリティに対して逆に動き，出来高や回転率に正比例している。
　呼び値との関係では，明瞭な結論は出せていない。最も高株価レンジ（次に高株価のレンジ）に適用される呼び値の効果はマイナス（プラス）であり，解釈不能だった。この点を除けば，先に紹介したChung-Charoenwong-Ding［2004］とは矛盾しない結果である。

（３）欠点

サンプル・サイズは最大58,464になるにも係わらず，各回帰式のサンプル数は３万超であり，データ欠損の多さが気に掛かる。
　そのデータ数欠損原因の１つに，呼び値刻みを該当月内に跨ぐ（該当の１ヵ月内に呼び値刻みが変化するほど株価が大きく変化した）銘柄は除外している，ことがある。該当の除外銘柄数は不明であるが，このデータ処理は研究目的を大きく変えることになるのではないかと思われる。株価変化が少ない銘柄の効果を測っているに過ぎない，のである。
　多重共線性については，月ダミー変数の間だけでも相関が高いのは簡単にわかるが，このダミー変数だけでなく，その他の変数間の多重共線性にも十分な注意が払われているとはいえない。

２－２－３　Depthの線形OLS回帰モデル～東証の分析

Swan-Pham-Westerholm［2008］は，2003年６月30日の東証改革を挟む，2003年３月１日から2003年９月30日までの日次データを用いて，線形OLS回帰分析，などを行った。サンプルは，指値注文があった，出来高トップの99銘柄である。
　2003年６月改革とは，東証はその時点で株価を決定する可能性が高い値段と，その値段における累計数量の情報を従来公表していたが，2003年６月30日（月曜日）からは，それまでの上下３本が上下５本に拡充された（東証HP参照などから引用），ことをいう。同時に，指値注文ブローカー名を非公開にするようになった。
　ちなみに，同研究には韓国証券取引所での同様な改革の効果の検証を含むが，ここでは省略する。
　被説明変数には，Depthの総価値の日平均（daily average of total value of depth）がとられ，常数項（計測結果はプラスで有意）と次の３変数が説明変数になった。日次出来高の自然対数値（同プラスで有意），レンジ（high low volatility；同マイナスで有意），2003年６月30日以前は０（以降は１）となるダミー変数（同プラスで有意）である。

（１）特徴

いくつか，目新しい視点と変数がとられている。まず，あげられるのが，Depth情報公開の効果をDepthの分布から得られる集計値を用いて分析している数少ない研究の１つである，点であろう。Depthについては，数量（株数）ではなく，総価値の日平均を用いるのである。
　ボラティリティには，レンジが用いられる。日次の分析にあたってはレンジ以外の選択肢はRVであるが，本来どちらを使うべきかの検証が必要になろう。この点の検証はなされていない。

【71 頁】

ダミー変数以外の説明変数は内生変数であるとみなす立場をとっている。そのため，計測法に２段階最小自乗法（2SLS）が採用された。2SLSでは，１期前の被説明変数と時価総額の自然対数値が操作変数として用いられた。

（２）計測結果と解釈

前２つの説明変数（出来高とレンジ）を分析に入れた理由は，Harris［1994］以来の研究をほぼ踏襲したからであり，期待される有意な符号をえている。日次出来高の自然対数値はプラスで有意，レンジはマイナスで有意であった。
　ダミー変数は，プラスで有意であったので，Depthの総価値は2003年６月30日以降増えた，ことになる。ところが，彼らの結論は，東証2003年６月改革はDepthには影響がなかった，という表現になっている。一体どうなっているのであろうか。さらに，この結論については，後述のデータ処理の問題，さらには他の問題点のため，保留しておかなければならないだろう。
　２SLSでも，係数の符号と有意性は変わらず，回帰モデルのスペックに内生性の問題が少ないことを示している。しかしながら，係数推定値の大きさはスペック間で大きく変わる。この点をどう解釈するべきか，何の説明も，何の仮説も提示されていない。

（３）欠点

東証出来高トップ99銘柄が，サンプルに採用され，東証の極く一部を代表するに過ぎない。また，サンプル期間において１日でも取引がなかった銘柄は除外されて99という数字になっている（元来サンプル数はいくつであったかの記述はない）。これらの点は，サンプル・セレクション・バイアスと呼べるかもしれない。
　Depthの総価値については，ほとんどの先行研究がDepthの数量（つまり株数）を用いているので，理論的背景，両変数の比較など，を詳しく展開するべきであろう。この点は売買単位が株価水準に応じて変わってくる点と関わっているものと考えられるが，一切，記述がない。
　2003年６月30日以前は３本値，以降は５本値，のDepthデータが入手可能である。これらの数値は基本的に不連続である。不連続性を修正する，などして分析や計測が行われている様子が見られない。どのような問題が内在しているかさえわからない。
　その他に，重要な欠点はいくつかある。東証の特徴である，呼び値刻みが株価に応じて変わる効果については，一切，記述がない。また，日次回帰式であるにも関わらず，曜日効果，月効果について全く考慮されておらず，どのような影響を及ぼしているかさえわからない。

２－２－４　呼び値刻みの引き上げ

シドニー先物取引所では，2009年５月11日17:00，３ヵ年債券先物の最小ティック刻みを0.5bpから１bpへ２倍に拡大させた。しかしながら，10年先物の最小ティック刻みと５本値気配の公開は，そのままになり，変更されなかった。
　Flint-Gerace-Lepone［2010］は，３ヵ年先物のDepthの自然対数値を，３ヵ年もののLn（出来高），同ボラティリティ，10年もののLn（出来高），同ボラティリティ，最小ティック刻み変更以降が１（以前は０）となるダミー変数に対して，2009年２月10日から８月13日までの日次データ（原データはもっとも近い時点の秒にタイムスタンプしたデータ）を用いて，線形回帰した。被説明変数のDepthには，最良気配Depthと総Depthがとられる。

（１）データとデータ処理

３ヵ年先物の最小ティック刻みの変更は2009年５月11日の17:00に行われたという理由で，５月11日と12日のデータは除外された。

【72 頁】

最良気配Depthと総Depthは，５分間隔のデータに基づいているため，１日の平均がとられた。出来高は日中の総取引高である。
　ボラティリティには，日中の最高の約定価格を最低の約定価格で割った比率の自然対数値がとられた。

（２）計測結果

先物のDepthに主として影響するのは，同年もののLn（出来高）やボラティリティである。
　計測された回帰式においては，最良気配Depthを被説明変数とする計測式が，総Depthのそれより，多少良好である。
　最小ティック刻み規模の引き上げは，有意なケースについては，３ヵ年もの最良気配Depthと総Depthを増やす。呼び値の効果について，ここまでの研究展望とは違い，明瞭な結果が出た。Goldstein and Kavajecz［2000］も，米国において１/８ドルから６セント（≒１/16ドル）への変更を分析した時系列分析で，刻みが細かくなって，指値注文の厚みは薄くなった，と報告している。これらの結果の意義は大きく，市場振興のため呼び値を粗くする方向に米国などは舵を切ったが，それを先駆ける研究であると言えるのではないかと思われる。
　しかしながら，競合すると考えられる10年もの先物のDepthへの影響は，最良気配Depthと総Depthの両指標とも，減る。ちなみに，スプレッドへの効果はマイナスである。これらの理由について十分な説明がなされていない。

（３）コメント

ダミー変数は，制度変更が一切なかった10年先物Depthを被説明変数とする回帰式でも有意である。Flint-Gerace-Lepone［2010］はその理由（例えば，注文が減った）を提示していない。有意であること以外に，その効果の大きさについても次のように問題がある。
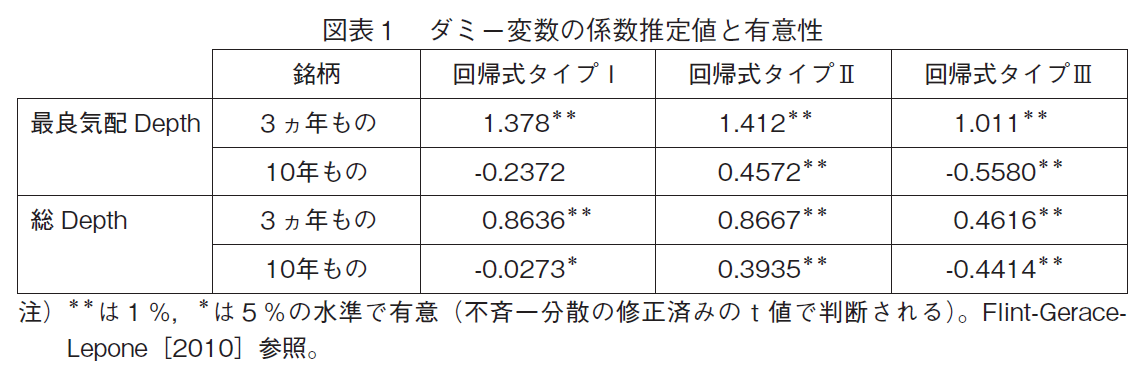
　呼び値刻み幅引き上げの効果について，Flint-Gerace-Lepone［2010］は十分な分析を行っていないので，以下に補充しておきたい。最小ティック刻み幅の引き上げは２倍なので，変更後のある特定のティック刻みについては，もし市場参加者の行動に何の変化もなければ，Depthも２倍になる。計測式においては，被説明変数はDepthの自然対数値なので，２倍になったDepthは被説明変数値をLn（２）＝0.69314だけ増加させる。計測式における説明変数側においては，ダミー変数の係数推定値がこの効果（正確には，その一部）を捉えている筈である。
　ダミー変数の係数推定値を図表にしてみたのが，以下の図表１である。計測は３つのタイプで行われたので，推定値は３つ得られている。
　最小ティック刻みが引き上げられた３ヵ年ものの，最良気配Depthだけが，どの計測式にお

【73 頁】

いても，Ln（２）＝0.69314より高い推定値を得ている。刻み幅の引き上げによって，最良気配（あるいはその周辺）での注文量が増加したものと考えられる。
　制度変更が一切なかった10年物では，いずれもLn（２）＝0.69314より大幅に低い推定値になっている。そして３分の２のケースでマイナスの推定値になっている。
　総Depthについては，３ヵ年ものの一部が多少大きな推定値になっているが，全般に推定値の水準は低い。最小ティック刻み幅引き上げの効果は，約定より離れた気配値に及んでいない，ということである。指値注文全体には必ずしも及んでいない，と解釈されるのではないかと思われる。

２－３　日中効果の分析

２－３－１　日中効果とは

一般に，リターンや取引量については，日中はＵ字型に推移することが知られている。寄り付き直後と大引け直前が高くなる（それゆえＵ字）現象がリターン，出来高などのいくつかの変数で観測されているのである。
　分析の時間間隔は，15分，30分などである。多く分析は，標準誤差などが計算され，隣り合う時間間隔の間では不確かであることが多いが，更に離れた時間隔間の間では違いは有意である事実も保証されている。

２－３－２　ディラー市場での日中効果

Frino-Lepone-Wearin［2006］は，2001年２月１日から2004年12月31日までのティック・データを用いて，オーストラリアの金融先物市場における90日もの，３年もの，10年ものレートの日中効果を計側した。

（１）特徴

オーストラリアの金融先物市場はディラー市場であり，ディラーの行動を理解することが計測結果の解釈にとって重要になる。Depthには，１分間隔毎の最良気配bidと最良気配askにおける数量の平均がとられた。そして，日次平均を差し引き，日次標準偏差で割る，正規化が行われ，正規化Depthと呼ばれた。
　計測には，取引時間を30分間隔の16区間に分け，それぞれにダミー変数（該当の時刻がその30分区間に入れば１，その他は０。ダミー変数相互の相関係数値は-0.06667）を付けて，各１分間の正規化Depthを16のダミー変数に対して定数項付きでOLSする方法がとられた。
　係数推定値が，当該時間帯の正規化Depth推定値になる。これらの正規化Depth推定値が作図され，特徴的な姿を浮かびあがらせている。なお，１分間の正規化Depthデータの30分平均値を計算して，この推定値と比較することはなされなかった。
　正規化は，日々の取引量などの変動から独立な，Depthの確率（度数）分布としての特徴を抜き出す。それゆえ，曜日効果問題を避けることが出来る。

（２）計測結果と解釈

正規化Depth推定値はいずれも寄り付き後と引け前１時間半の間強く有意になる。正規化Depth推定値の大きさについて満期の違いは明瞭に観察されなかった。
　正規化Depth推定値は，日中，寄り付きから引けにかけて，一様に逓増する（図表２参照）。日中の取引量が周知のＵ字型であることも確認されたが，それとは好対照であり，この逓増現象はディラーの行動から引き起こされたと考えられた。それが，日を超えて在庫を持ち越した

【74 頁】

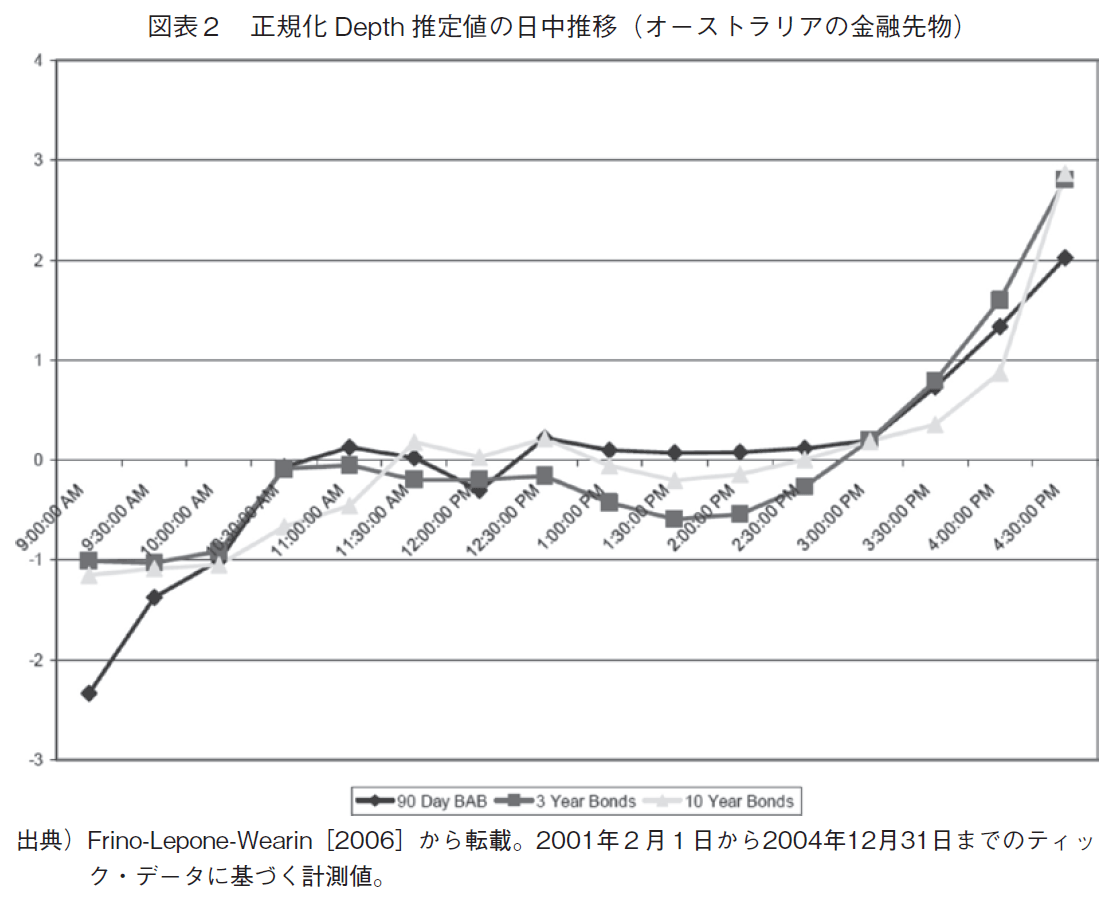
くないディラーは売り買いをつけるために注文を多く出す，という仮説である。この点はHFT行動とも共通する。
　大引けにかけて，さらに，約定がなされ次の約定までにかかる約定間隔時間も，短くなるという実証結果もあれば，この主張はさらに確実になろう。残念ながら，このような計測はなされていない。

３　Depth情報と非表示注文について

３－１　問題点の指摘

（１）海外の実情と実証分析

世界の主要国において，取引所の立会外取引あるいはダークプール・証券会社の内部付合せにおいてではなく，取引所の立会取引において，トレーダーは注文を非表示あるいは非公開にすることが認められている。表現は様々で，Undisclosed Orders, Hidden Orders（Hidden Liquidity），Non-displayed Ordersなどがある。説明文では，さらに，unexpressed と latentが加わる。注文の100％を非公開にできる場合もある。
　非表示注文については，米国の他，英国（LSEのSETS），ドイツ，カナダ（トロント証券【75 頁】取引所），オーストラリア，アイスランド，スペイン（マドリッド証券取引所Bolsa de Madrid），ユーロネクスト，コペンハーゲン株式取引所，チャイエックス可視（CHI-Xvisible），などで類似の仕組みが採られている。特に一部の取引所は特徴的であり，そのデータの一部を事後利用可能にしている。
　Euronext Parisは2001年４月23日に，業者名を非公開にし，非表示注文制度を導入した。アイスランドのECNはもっとも活発に取引されていた３つのETFの指値注文板の公表を2002年９月にやめ，市場の質は悪化したとする研究がある。
　Belter［2007］など，非公開Depthが流動性供給に与える役割，その情報の価値を分析する研究があらわれ始めており，その意義は大きい。
　呼値刻み，値決め方法，などと同様の，注文と執行方法の多様化であり，市場の魅力を高めているという捉え方がある。他方で，見えない市場は参加者の信頼を損なうという捉え方もある。
　非表示注文を考察するには，まず指値注文するかどうかがどのような変数に依存するか，考えてみる必要がある。成り行き注文では，あえて非表示にする誘因は小さい。指値注文することが決められれば，投資家・トレーダーは次にその内どれだけの数量を非表示にするか，を決める必要がある。
　このような視点から先行研究を展望してみることが必要である。なお，実験市場技法，遺伝的アルゴリズム（GA）などの新技術による分析，さらには債券市場の分析は展望から省いた。ちなみに，Kozhan and Salmon［2012］は遺伝的アルゴリズム（GA）を用いて情報のあるなし

【76 頁】

がどういう影響をもたらすかを分析し，情報公開が良い効果をもたらすことを示している。非公開化は債券市場では好ましくない結果をもたらす，という研究もある。

（２）非表示注文（非公開比率）の大きさ

そもそも非表示注文（非公開比率）の大きさはどれ位なのだろうか。国によって，年次・時期によって，商品（指数か個別銘柄か，など）によって，多少の差はあるが，株式については少なくとも10％を超え，50％にも達することがあり，さらにそれを超える場合もある。Belter［2007］が明らかにするところでは，1999年10月から12月のコペンハーゲン証券取引所の最良気配ではおよそ35％が非表示注文で，それから離れると５から10％ポイント低くなる。
　Cebiroglu and Horst［2012］が引用する2003年から2009年までに発表された研究で（現時点ではほとんどが入手不能）は，次のような数字が計測されている。2003年発表の研究では，NASDAQ全体のおよそ25％が非公開であることを見出している。スペインの全取引の26％（2008年発表の研究）が非表示である。さらに，ドイツのXetra株式取引所では（2009年発表の研究），2004年の１月２日から３月31日の期間，アイスバーグ注文平均株数は指値注文のそれの12-20倍にもなり，注文の9.3％，取引される数量の15.9％がアイスバーグ注文である。
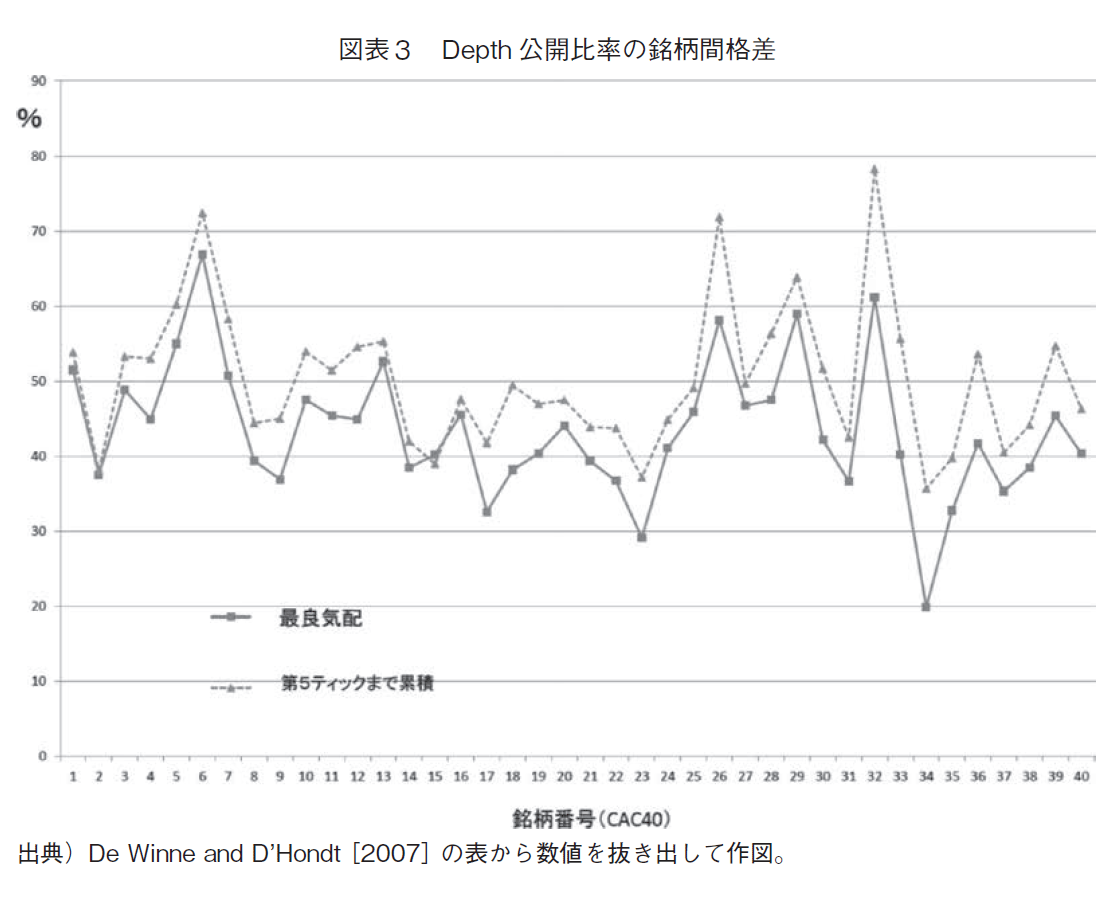
　2002年の最後の３ヵ月を調査したDe Winne and D’Hondt［2007］は，フランスCAC40の最良気配から５番目までの気配の注文では45％が非表示である，（彼らの年次不明の他の研究では，CAC40全流動性の27.2％，同じくベルギーBEL20の20.4％，が非表示である。しかしながらCAC40の最良気配に至っては50％にも達する）と報告している。
　Depth公開比率の銘柄間格差を示した図表３では，１銘柄を除いて，最良気配の非公開率は高く，銘柄よっては70％近くにもなることがわかる。しかしながら，一般に，非公開にする比率は銘柄間で大きく変わることはないように見える。
　Bessembinder, Panayides and Venkatamaran［2009］は，2003年４月中にEuronext Parisで取引された高低様々な流動性（最低は平均１日１回の取引）の100銘柄を分析し，44％が非公開であることを報告している。

３－２　日米の事情

（１）米国の実情

日本においては主として証券会社が顧客投資家向けのサービスとして複雑な注文タイプを提供しているが，市場（取引所）間競争が極めて激しくなった米国では，取引所自身が提供するようになっている。
　具体的には，米国では，価格優先・時間優先の原則を崩す要因となるような，注文は受けたが板に表示しないタイプ（非表示注文），受けた注文とは違う気配に注文を仮置きするタイプ（プライス・スライド）が存在する。
　市場参加者が出せる注文は，米国では，表示注文と非表示注文に分かれる。非表示注文は存在自体が第三者には全くわからない。さらに，非表示注文されていた注文も，参加者自身の都合（当然，その背景に経済的要因が存在するだろう）で，それが表示され（表示注文に変更され）るようになると，突然板に現れてくる。
　プライス・スライドされ，本来の注文の気配とは違う気配に仮置きされていた注文も，ある時突然に参加者自身の都合で，もともとの気配の指値注文に戻れば，表示注文として突然板に【77 頁】載ってくることになる。
　これらの注文タイプの存在自身がDepth情報の信頼性を大きく損なわせる。影響はそれにとどまらない。一般の市場参加者の取引は先回りされてしまう恐れがある。そして，そういう事態が知られるようになれば，トレーダーは先回りされている，と理解するようになり，取引所に指値を提示しておく意欲が後退する。その結果，取引所の板が薄くなる。これにより，大口注文がより執行しづらくなり，取引所外市場への注文流出が加速する。そして市場分裂が拡大するという悪循環に陥る恐れがある。

（２）日本の事情

東証では，成行注文と指値注文という基本的な２つの注文種類に，寄付条件，引け条件，不成条件，IOC条件の４つの条件を付けることができる注文だけが受け付けられる。これらは，価格優先・時間優先の原則に基づき，東証のマッチング・エンジンであるarrowheadで処理される。
　結果として時間優先の原則を崩すような執行待ち行列の順位変更（キュー・ジャンピング）の問題は生じない。そもそも，米国で存在するような，当該原則を崩す要因となるような，注文は受けたが板に表示しないタイプ（非表示注文），受けた注文とは違う気配に注文を仮置きするタイプ（プライス・スライド）は無い。
　東証では，最低限必要であると考えられる，非常にシンプルなオーダー・タイプしか導入されておらず，それらは誰もが容易に理解できるものとなっている（これらは大墳［2014］が用いている表現である）。これをもって，より公正かつ秩序ある市場を維持することとなっている。
　世界の多くの取引所，取引プラットフォームで売買指図の１つとして非表示注文（主にアイスバーグ注文）が可能となっているが，わが国ではPTSのSBIジャパンネクストとチャイエックス・ジャパンがアイスバーグやペッグの注文指図を受け付けているに過ぎない。
　ちなみに，アイスバーグ（iceberg）戦略では，大口注文を執行中であることを市場に悟られないように，板情報をできる限り変化させず少量ずつ自動執行する。アイスバーグ注文は，その一部を開示しないという意味で隠れた注文の一形態である。また，ペッグ（pegging）戦略では，例えば最良気配に自動追随するように指値注文を入れることで最良な価格で売買することを目指している。

４　研究の方向性

４－１　論点整理

株式市場のDepthは株価上昇（株価水準の高さではない）や取引の増加と比例し，株価水準やボラティリティと反比例する，という結果がほぼ共通して出ている。しかしながら，従来計測結果が様々であった呼び値の効果については，呼び値が粗くなる方がDepthは増える，という研究結果に落ち着きかけている。一応得られたこのような実証結果をもとに，さらに詳しく項目ごとに説明しておこう。

（１）呼び値の刻みとDepth

刻みが大きければ，流動性を提供すればするほど，利益があがる。この点はHarris［1994］などにも，記述されている。１ティックで抜ける鞘は大きくなる，と投資家が表現する事柄で【78 頁】ある。この利益率は，刻み幅を株価で割った比率（ティック株価比率）に比例する。
　さらに当該銘柄に株価変化が予想される（あるいは，その他の投資機会がある）とすれば，より多くの投資家が指値注文を入れる。他方で，株価水準が高いほど，刻みは大きく設定される傾向がある。それゆえ，株価水準が高いほど，ティック株価比率は下がるので，Depthは減る。

（２）売買単位と流動性

株価水準が低い銘柄の売買単位は大きいが，株価水準が高い銘柄の売買単位は小さい傾向がある。株価水準が高い銘柄の売買単位は小さいので，注文が出された回数は多くても，日次平均注文株数は少ない。このような高株価水準銘柄は，日次平均注文株数は少ないが，日次平均注文金額は多いので，流動性が高いと言ってよいのだろうか。

（３）呼値の刻み幅を超える株価変動

サンプル期間で同じ呼値の刻みを維持している個別銘柄を分析の対象として限定（具体的に述べれば刻みを跨げばサンプルから除外する）して検証することがなされることが多い。しかしながら，これは株価変動パターンが類似した銘柄のみを検証対象としていることになっており，その範囲の研究に留まる。東証の分析と言えるには，サンプル・セレクション・バイアスを起こしているので，計測結果では係数推定値，その有意性などが信頼できない。
　この分析の限界を乗り越えるためには，サンプルを短い期間でとればよい。例えば数分間隔であれば，まったく問題はない。１日期間でとっても，呼び値が刻みを超えることはほとんどないだろう。

（４）ボラティリティ

ボラティリティには，レンジが用いられることが比較的多い。例えば，日次データの分析では，日中の最高の約定価格を最低の約定価格で割った比率の自然対数値，さらに，秒データに基づく場合には，５分間の最高の約定価格を最低の約定価格で割った比率の自然対数値の日中平均，である。

４－２　Depthの比率

（１）Depthとその比率の特性

Depthの諸統計量を計算してみると分析に役立つ。１本値Depthとは最良気配値における注文量，５本値Depthは最良気配値から５つ離れた価格・気配値までの注文量合計，であるとする。
　Depth分布の特徴を把握するには，１本値Depthと５本値Depthの比較で行うのが良いだろう。１本値Depth/５本値Depth（小数点表示）で最良気配への分布集中度あるいは分散度が表せる。１本値Depth/５本値Depthは，当然，市場の厚みを示す代理変数ではない。Depthの姿と動きをみることによって，約定価格の次の動きを探るもので，指値注文行動を捉えることが狙いとなる。
　Depthの比率は，５本値だけでなく，データが公表されている限り任意の数字をとり得る。それは最大１の値をとる。
　Depthを計算してみる際，このような比を銘柄ごとに一定期間例えば１年間計算してみることが有用であろう。

（２）インデックス間の差異～米国の場合

先に紹介したAngel-Harris-Spatt［2011］では，S&P500銘柄の１本値Depth/６本値Depthは，【79 頁】 2003年12月以降2009年１月までのおよそ５年の間に，0.20（＝2,000 / 10,000）から0.05625（＝4,500 / 8,000）に大きく低下している。それに対してNYSE全銘柄のこの比率は同期間0.50（＝1,000 / 2,000）から0.32（＝1,600 / 5,000）へと下落しているに過ぎない。既述のように厚み自体は大きく変化していないRussell2000については0.40（＝800 / 2,000）から0.20（＝1,000 / 5,000）へと分布は大きく変化した。
　この期間に起こった事柄はこれらの数字をそのまま捉えると，それゆえ，S&P500銘柄とRussell2000の６本値Depthを相対的に大きく増大させた，ということである。
　厚みの増加は，アルゴリズム取引や高頻度取引によるものであると想定された。このような取引のターゲットになっているのが高流動性銘柄に偏っていることが疑われる。その結果，高流動性銘柄の流動性がますます拡大し，そうでない銘柄の流動性は変わらないという二極化現象につながる，という解釈がなされる。
　しかしながら，既述のように，Angel-Harris-Spatt［2011］が非表示注文をどのようにどう適切に取り扱ったかが明瞭でないため，この結論は暫定的なものにとどまる，といわざるをえない。

（３）インデックス構成銘柄のDepth比率～CAC40の場合

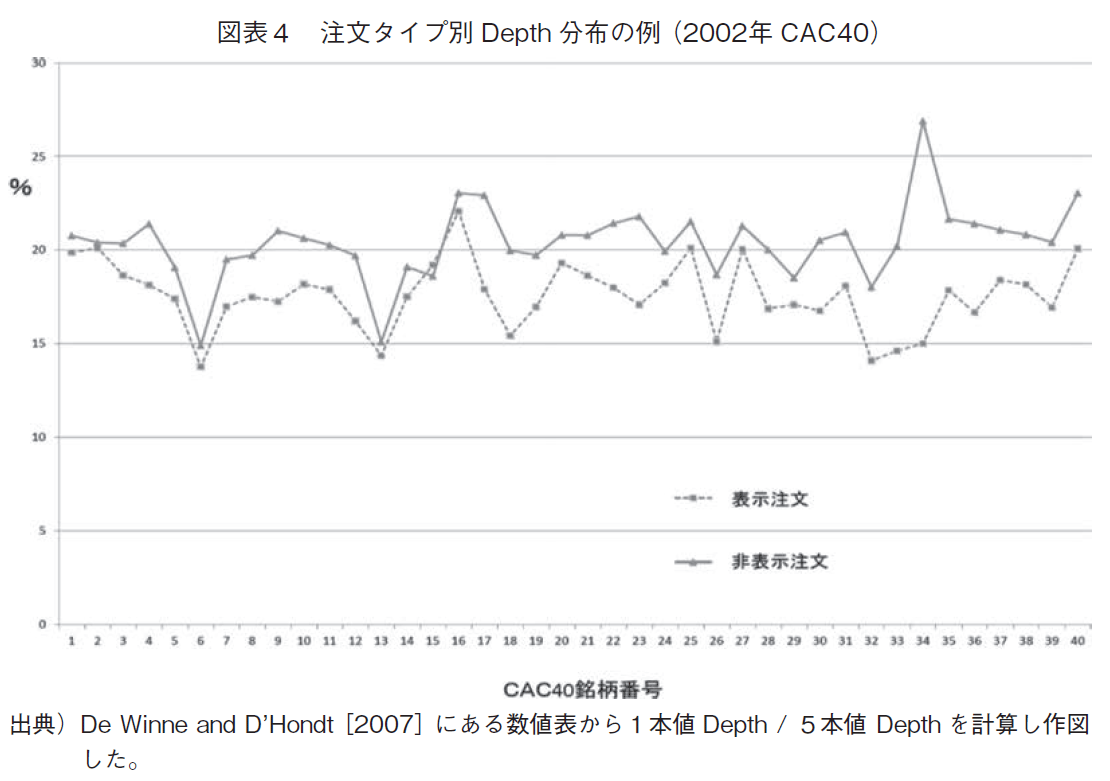
フランスの非表示注文を分析したDe Winne and D’Hondt［2007］は，Depth分布についても計算している。最良気配のDepthが５ティックまで離れた累計Depthに占める比率を表示注文と非表示注文で図示した図表４を見れば，CAC40構成銘柄の表示注文については，2002年10月から12月の期間，最良気配におけるDepthは５ティックまで離れた気配の累計Depthの20％弱になっている。５分の１のエィリアに５分の１の頻度であるということは，最良気配近辺での集中度は高くなかったということである。

【80 頁】

非表示注文については，１銘柄を除いてこの比率は数％高く，最良気配近辺での集中度は表示注文と比較して高くなっている。最良気配から（５ティックまで）離れる程，注文は表示される傾向があることを示している。

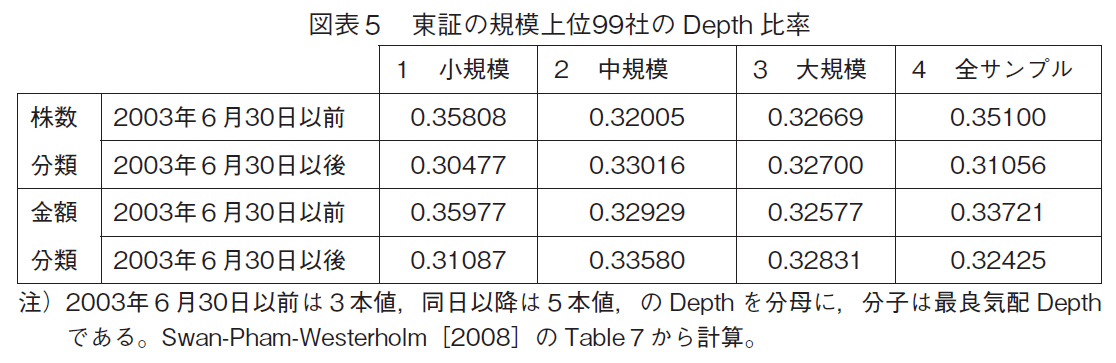
（４）東証の規模上位99社のDepth比率

先に紹介したSwan-Pham-Westerholm［2008］が，論文中のTable７において，全Depthと呼んでいるものは2003年６月30日以前は３本値，以降は５本値，のDepthに相当している，と解釈される。その意味でデータは非連続である。2003年６月30日以前の方が分母が小さく，他の条件が同じならば，Depth比率は大きくなってしまう。
　これを前提に，分子を最良気配Depthにして，Depth比率を計算してみると，東証上場のトップクラス99企業では0.30から0.36の間である（図表５）。株数や時価総額の分類でみても，比較的安定した比率の数字であるとみなすのが，正当であろう。これは，経過した期間も短く，また2003年東証改革の影響も小さく，大きな差を生まなかった，のが理由と考えられ，現時点では参考程度と捉えるべきであろう。

（５）非表示注文のDepth分布とその集中

Cebiroglu and Horst［2012］は，2008年10月から2009年３月の米国S&P500構成全銘柄の10ティックまでの分次データを用いて，表示注文の80％は最良気配から離れた５つの気配のもとでのDepthに分散している（残りの20％はさらに離れて位置している）が，非表示注文は集中しており最良気配により近い２，３の気配におけるDepthに限られる，と報告している。この点はDe Winne and D’Hondt［2007］の発見と整合的であるが，より明瞭である。
　ちなみに，彼らは非表示注文が存在するのは数限られた大規模トレーダーと関係していると考えたが，十分な検証はない。もっとも，非表示注文は表示注文より分布は集中している現象（非表示注文のDepth分布の集中化）は，分析が少ないだけでなく，これまで指摘されることも少ないので，貴重な研究である。

（６）含まれる情報の視点

Depth比率における，分子と分母それぞれが持っている情報量に差異がある，と捉える考え方が根底にある。確かに，約定価格から離れる気配値ほど，直後の価格形成に果たす役割は異なり，価格形成に及ぼす影響は小さいだろう。しかしながら，視野を更に先に広げてみると，大きな価格変化を及ぼす可能性は秘めていると言えるだろう。

【81 頁】

５　残された課題

ティック・データでは，出来高，売り買い両側の１本値Depth・５あるいは10本値Depthの５系列あれば，さらに突っ込んだ分析ができるはずであるが，そのような研究は多くない。さらに，非表示注文データが利用可能であれば，研究対象となるトピックスは飛躍的に増加する。その方向への研究が蓄積されることを期待したい。
　Depthの時系列推移も重要な変数である。累積時系列Depthは，過去一定期間（最長でも同日のデータをとる，つまり１日が妥当と思われる）の系列である。売りと買いの差額（前者─後者）をとると，最良気配や取引価格へはマイナスの影響を及ぼすことが予想される。

付録　あるべき回帰分析～各変数の考察

１本値Depth/５本値Depthを次の説明変数群に対して回帰する際，先行研究に基づくとすると，どのような点に注意しなければならないか述べてみよう。時系列で回帰すべきか，クロスセクションで行うべきか，データ処理に検討を加える点は残し，ここでは変数間関係について議論することにする。説明変数は次である：業種ダミー，呼び値の刻みあるいはLog（株価），PTS間競争ダミー，日経平均構成銘柄ダミー，など。具体的に示すため，PTSのなかでもJNXのDepth比率を説明することを前提に展開しよう。また，被説明変数のデータは公開注文でしか利用可能でないので，非公開比率は銘柄間で安定しているという仮説を前提にしている。

Ａ－１.　被説明変数

１本値Depth/５本値Depthは，ティック毎，１秒毎，200秒毎，数分毎，１日毎等のどれにするか検討しなければならない。Depthはaskとbid両側の和となる。

Ａ－２.　説明変数

（１）呼び値の刻み

株価水準に応じた取引所，JNXの呼び値刻み0.1，0.5，１，５，10，50，100円などを使うことになる。それらの自然対数値を用いる方法と７つのダミー変数にする方法との２つがある。
　ダミー変数法は，2013年まであったJNXの呼び値刻みが東証と比較で持つ優位性を，より適切に計測するものと考えられる。係数値の大きさと有意性の高さは，その呼び値刻みの優位性を示すだろう。

（２）PTS間競争ダミー

株価が3,000円から5,000円，30,000円から100,000円，300,000円超なら１，それ以外は０というダミー変数になる。
JNXに対してCHI-Xの呼び値の方が細かい場合に１，そうでない場合０になれば，CHI-Xダミーとも呼べる。

（３）日経平均ダミー～市場を代表するインデックスの構成銘柄

日経平均，という市場を代表するインデックスの構成銘柄については，ダミーを付ける。流動性の代理変数になる可能性がある。

【82 頁】

（４）ボラティリティ

追加するべき説明変数には，約定価格の変化率の絶対値，あるいはその一期遅れの変数，レンジなどが候補になる。

（５）業種ダミー

もし株式リターンやスプレッドが非説明変数であれば，業種ダミーは説明変数として余り有意でないかもしれない。
　しかしながら，3.11での建設，土木などの業界での反応，南欧州債務危機で金融部門が抱える問題，などイベントの影響の一部を捉える，ものと考えられる。
　ふつうは製造業とサービス業で分けるが，どのような業種ダミーを用いるかは要検討である。東証銘柄番号の大番号毎に違うダミー変数とするのが１つの方法でもある。
　なお，Depthに対する役割という視点からは，業種ダミーの役割は従で，コントロール変数という取り扱いになろう。

Ａ－３.　その他の変数に対する考察

Depthの比率ではなく，Depthを被説明変数とする場合，曜日効果，月効果，さらにマクロ効果，グローバル効果を考慮する必要がある。これらの変数として何をどう選択するのかは一般に困難な作業である。
　具体的に述べれば，2011年の3.11東日本大震災の影響を除去するためにイベント・ダミーとして何日取るか。３日はどうか，あるいは５日（実質１週間を意味する）はどうか，など必ずしも経済的根拠が十分にあるとは言えない検討が必要になってくる。
　欧州債務危機は，株価だけでなく，為替レート，CDSレート，などにも影響が出ている。しかしながら，東証とJNXの両方だけでなく，様々なDepthにも同様に影響するので，２つDepthを（東証とJNXの２市場を適切に）比較する回帰式であれば考慮する必要はない。3.11についても同様である。
　曜日効果は明瞭に存在するので，曜日ダミー変数は必要である。しかしながら，ダミー変数の入れ方は工夫を要する。更に月次ダミーについても同様な問題が存在する。これらの時系列アノマリーも，市場間に違いがなれれば，計測方法によってはキャンセルアウト・相殺する。この点を利用した計測法が必要になってくる。
　実際，曜日効果などの時系列アノマリー，金融危機などのグローバルやマクロ要因は，被説明変数がDepth比率となればそれらの効果はキャンセルされる。

Ａ－４.　各変数の効果と予想される符号

（１）呼び値の刻みあるいはLog（株価）

Goldstein and Kavajecz［2000］は，刻みが細かくなって，指値注文の厚みは薄くなった，と報告している。このGoldstein and Kavajecz［2000］に従うと，株価水準が高くなるにつれて刻みが粗くなるので，予想される符号はプラスである。
　呼び値の刻みとLog（株価）は相関する。それゆえ，呼び値の刻みに代えて，Log（株価）でも計測してみる，ことが考えられる。

（２）PTS間競争ダミー

該当の株価では，CHI-Xの方が，５分の１から10分の１，呼び値の刻みが細かいから，予想【83 頁】される符号はマイナスである。

（３）日経平均ダミー～市場を代表するインデックスの構成銘柄

Angel-Harris-Spatt［2011］は，米国において，S&P500銘柄に圧倒的に大きな市場の厚みがあること確認している。Angel-Harris-Spatt［2011］に従うと，日経平均構成銘柄ダミーの予想される符号はマイナスである。

（４）ボラティリティ

Depthはボラティリティに対して逆に動く傾向が検出されているが，Depthの比率については先行研究がない。

（５）業種ダミー

業種によって，リターン水準が違い，その変動パターンも異なってくる。それゆえ，１本値Depth/５本値Depthに対する効果は違ってくる。どの業種にアルゴ，HFTがなされているか，という発見ができるかもしれない。

参考文献

Angel, J. J., Harris, L. E. and Spatt, C. S., ［2011］, “Equity Trading in the 21st Century,” USC working paper, Feb. 2010.

Belter, K., ［2007］, Supply and Information Content of Order Book Depth: the case of displayed and hidden depth, May 2007. SSRN-id1068163

Bessembinder, H., Panayides, M. and Venkatamaran, K., ［2009］, “Hidden Liquidity: An Analysis of Order Exposure Strategies in Electronic Stock Markets,” Journal of Financial Economics, 94, pp.361-383.

Buti, S. and Rindi, B., ［2013］, “Undisclosed Orders and Optimal Submission Strategies in a Limit Order Market,” Journal of Financial Economics, 109, 3, pp.797-812.

Cebiroglu, G. and Horst, U.,［2012］, “Hidden Liquidity: Determinants and Impact,” SFB 649 Discussion Papers 2012-023, Humboldt University, Berlin, Germany. http://sfb649.wiwi.hu-berlin.de/papers/pdf/SFB649DP2012-023.pdf

Chung, K. H.,［2005］, “Liquidity and quote clustering in a market with multiple tick sizes,” Journal of Financial Research, Vol. XXVIII, No. 2, Summer 2005, pp.177-195.

Chung, K. H., Charoenwong, C. and Ding, D. K., ［2004］, “Penny pricing and the components of spread and depth changes,” Journal of Banking & Finance 28, pp.2981-3007.

De Winne, R. and D’Hondt, C., ［2007］, “Hide-and-Seek in the Market: Placing and Detecting Hidden Orders,” Review of Finance, 11, pp.663-692.

Flint, A., Gerace, D. and Lepone, A., ［2010］, Market Quality Surrounding a Tick Size Increase: Evidence from the Sydney Futures Exchange, EFMA, 2010.

Frino, A., Lepone, A. and Wearin, G.,［2006］, The Intraday Behavior of Market Depth in A Competitive Dealer Market: A Note, 2006.

Goldstein, M. A. and Kavajecz, K. A., ［2000］, “Eighths, sixteenths and market depth: Changes in tick size and liquidity provision on the NYSE,” Journal of Financial Economics, 56, pp.125-149.

Harris, L., ［1994］, “Minimum price variations, discrete bid-ask spreads, and quotation sizes,” Review of Financial Studies 7, pp.149-178.

Harris, L., and Panchapagesan, V.,［2005］, “The Information Content of the Limit Order Book: Evidence from 【84 頁】 NYSE Specialist Trading Decisions,” Journal of Financial Markets, 8, pp.25-67.

Kaniel, R. and Liu, H., ［2006］, “So What Orders do Informed Traders Use?” Journal of Business 79, pp.1867-1913.

Foucault, T., Moinas, S. and Theissen, E.,［2007］, “Does Anonymity Matter in Electronic Limit Order Markets?” Review of Financial Studies, vol. 20（5）, pp.1707-1747.

Kozhan, R. and Salmon, M. H., ［2012］, “The information content of a limit order book: the case of an FX market,” Journal of Financial Markets, Vol.15（No.1）. pp. 1-28.

大墳剛士［2014］『米国市場の複雑性とHFTを巡る議論』 JPXワーキングペーパー特別レポート，2014年７月。

Perotti, P., Rindi, B. and Fredella, R.,［2012］, Minimum Trade Unit Regulation and Market Quality, March 2012.

Swan, P. L., Pham, T. P. and Westerholm, P. J.,［2008］, Contrasting the equity market transparency reforms in Korea and Japan: Endogenous effects on volatility, spreads and depth, 2008.

辰巳憲一［2015］「HFTの金融仲介機能：その行動と影響に関する堰モデルの展開」『学習院大学経済論集』，2015年１月，pp.167-188。