�����i�ɂ��������҂̒ቿ�i���x�̈�Ɋւ���l�@
�`�O�[�e���x���O�����̃��f�����̎��݂ƍō����v�ݏo���i�Œ�j���i�|�C���g�̔����`
�w�K�@��w�@�o�ϊw���@�����@�@�@�@�@�@�@�@�@�@��c�@����
�w�K�@��w�@�o�ϊw���@�u�t�@�@�@�@�@�@�@�@�@�@�|���@�r�q
�w�K�@��w�@�o�ϊw���@�u�t�@�@�@�@�@�@�@�@�@�@�R���@���q
�{�e�ł́CID-POS �f�[�^���g���C�l���Ƃ̉��i���x�ŃO���[�v�������s���C�u���i�̐^�̎��v�Ȑ��v�ƌ�����O�[�e���x���O�Ȑ����o�������C����҂̉��i���x�O���[�v�ʂł��̃O�[�e���x���O�Ȑ��`���ǂ̂悤�ɕω����邩����������B����ɁC�Ȑ������ɒቿ�i���x�̈悪���݂���Ȃ�C�ǂ��܂ł̍����i������҂ɒ�R���Ȃ���e����邩�𖾂炩�ɂ���B�܂��C����҂̏��i�ɑ��鉿�i���x�ɒ��ڂ��C���v�ő剻�ݏo���i�Œ�j���i�|�C���g�i���i�|���j�̐�����s���B
�v���X�y�N�g���_�C�O�[�e���x���O�����C���v�Ȑ��C���i�C���i���x�C���v�ő剻
���i�Ɣ̔����ʂ̊W���Ȃ킿���i�̎��v�Ȑ��́C���̎��ۂ̌`�ǂ������`�����Ă��邩�ɂ��Ă͏\���ɂ͌�����Ă��Ȃ�1�j�B���Ȃ��Ƃ�����܂őz�肳��Ă����قƂ�ǂ̌`�C����t���̐��`���Ϗ�^�̋Ȑ��`���ł���B�������C����҂ɂ́C�e���̓��I�Q�Ɖ��i�ߕӂɉ��i���x�̒Ⴂ�̈�C�܂艿�i�ɔ������Ȃ��̈悪���݂���Ƃ������i�̎��v�Ȑ��Ɋւ���O�[�e���x���O�������]�����炠��iSimon 1989�j�B����܂ŁC���i���x�̒Ⴂ�̈�̑��݂̉𖾂Ɍ����Ă��������݂��Ȃ���Ă������C���܂����̑��݂͖��炩�ɂ���Ă��Ȃ��B���̌����Ƃ��āC����ɗp����ꂽ�f�[�^�̖�肪����B����͏W�v���x���f�[�^�iPOS�f�[�^�j�ł���C�l�f�[�^�𗘗p�ł��Ȃ��������Ƃɂ��\�����傫�����낤�B
�{�����ł́C���������g���R�[�v�����ۂ�i�ȍ~�C�R�[�v�����ۂ�j��ID-POS �f�[�^���g���C���i���x�Ɋ�Â��ď���ҕ��ނ����C���i���x�т��ƂɃO�[�e���x���O�����̉𖾂����݂��B
�y2�Łz���I�Q�Ɖ��i�i�l�����i�j�ߕӂ̉��i���x�̒Ⴂ�̈�̑��݂��m�F�����C����܂ł̉��i�̎��v�Ȑ��`�ɐV���Ȓm���������邱�Ƃ��ł���B����ɁC������܂łȂ����҂ɒ�R���Ȃ���e����邩�����炩�ɂȂ邱�ƂŁC�ō����v�ݏo�����i�|�C���g�̐��肪�\�ƂȂ�B
�O�[�e���x���O�����Ɋ֘A���鉿�i���_�Ƃ͌o�ϊw�C�S���w�ɂ����ď]���_�����Ă������i���_�ł���B
�Q�|�P�D�v���X�y�N�g���_����̓��o
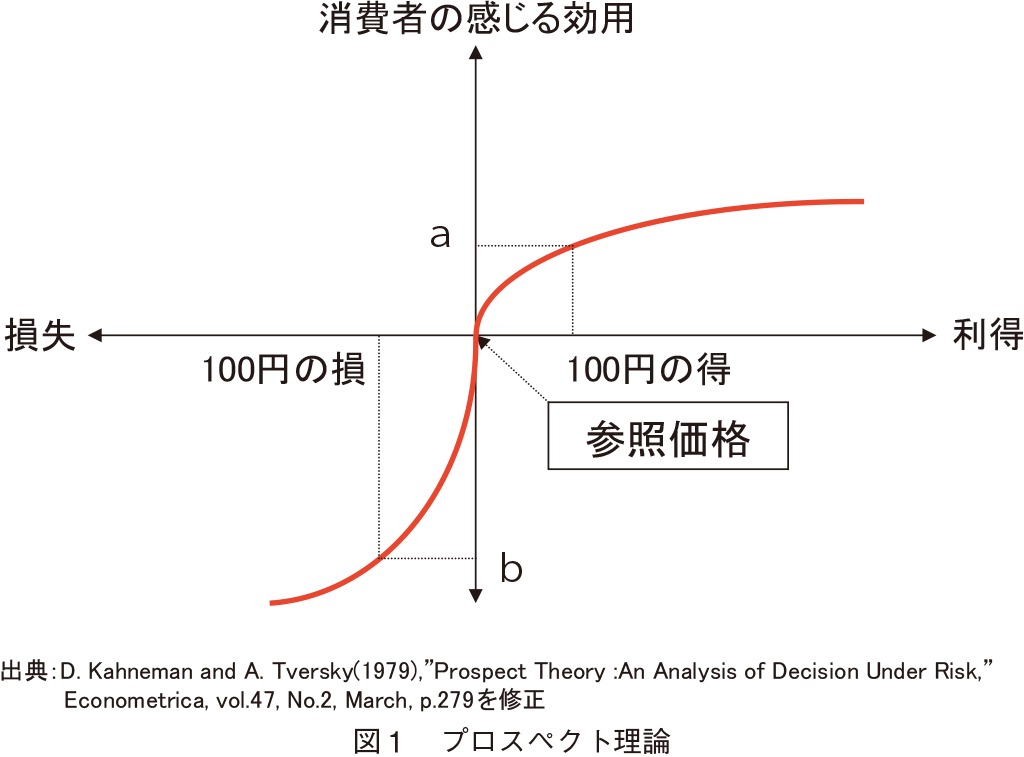
�v���X�y�N�g���_�Ƃ́C���i�̍���Ɋւ������҂̔����̈Ⴂ�����������̂ł���C���I�Q�Ɖ��i���x�[�X�Ƃ��ď��i���i�̍���̐�Βl���������ꍇ�ɂ́C���������������������ɂ�苭���C���p�N�g��������Ƃ������e�ł���2�j�B�}�\����ƁC�}�P�̂悤�ɂȂ�B�������C��c�E���R�E����i2002�j�́C�}�P�ł͂܂��s�\���ł���Ǝw�E�����B���R�Ƃ��āC����҂͓��I�Q�Ɖ��i�ƌĂ�鏤�i���i�̍���f���邽�߂̊���i���L�����ɑ��݂��Ă���C����҂͂��̓��I�Q�Ɖ��i�̋ߕӂɉ��i���x�̒Ⴂ�̈�������Ă���̂ł͂Ȃ����Əq�ׂĂ���B����ɁC����͐S���w�ɂ����čl����ꂽ���_�ł���u�����Δ䗝�_�v�Ɓu�X�C�b�`���O�E�R�X�g�v�̑��݂��e�����Ă���Əq�ׂĂ���B
�Q�|�Q�D�����Δ䗝�_�ƃX�C�b�`���O�E�R�X�g�̑��݂��e��
�����Δ䗝�_3�j�Ƃ́C�u�l�́C�߂��̂��̂Ɋւ��ẮC���ۂ̍��������̈ʒu�͋߂��ɂ���ƒm�o���邪�C���̃|�W�V�����������ꍇ�ɂ́C���ۂ̋����������Ȃ艓���Ɋ����Ă��܂��v�Ƃ������e�ł���B�O�҂͓������ʁC��҂͑Δ���ʂƌĂ��B��������i�ɒu��������C���I�Q�Ɖ��i�̑����̉��i���͓������ꂻ��قNj����͒m�o����Ȃ����C�傫�������Ɖ��i���͎��ۂ̍������Δ䂳��C�����m�o����邱�ƂɂȂ�B
�X�C�b�`���O�E�R�X�g���_�ɂ����ẮC���I�Q�Ɖ��i����ɏ���҂��u�����h�I��������ۂɁC�������i�Ƃ̉��i���ɉ����āC�u�����h�̐�ւ��̍ۂɔ�����������S���I��R�C��ԁC���K�I���S�⎸�s�̃��X�N�������邱�Ƃɂ���āC�X�C�b�`����C���Ȃ��̔��f���Ȃ����B�������i�Ɠ��I�Q�Ɖ��i�̍��̑傫�����X�C�b�`���O�E�R�X�g������ƁC臒l���C�u�����h�X�C�b�`���O����X��������4�j�B�����}�\����Ɛ}�Q�̎����̂悤�ɂȂ�C��������炩�ɋȐ��łȂ��Ɛ}�̓_���̂悤�ɂȂ�B

���̐}�Q�����E���]�����C���S���̉��i�Ɣ��㐔�ʂƂ̊W�����������̂��C�}�R�ł���B���ꂪSimon�i1989�j�̏q�ׂ��O�[�e���x���O�����Ɋ�Â����v�Ȑ��ł���B�d�v�ȉ��i�|�C���g�Ƃ��Ă��鍂�����̉��i�|�C���g�͂����炭���v�z�ő剻�̃|�C���g�ł���C����ȏ�̍����i�ł���Ƌ}���Ɏ��v��������|�C���g�ł���B�܂����̒Ⴂ���̉��i�|�C���g�͎��v���y4�Łz�h�����邽�߂̃Z�[���X�E�v�����[�V�������ʼn��i��������ꍇ�ɂ�����Ⴍ���Ȃ��Ɣ���ω����N���ɂ����C�Ӗ����Ȃ��|�C���g�ƂȂ�B
�Q�|�R�D�O�[�e���x���O����
�O�[�e���x���O�����Ƃ́CSimon�i1989�j�ɂ���1976�N��Gutenberg �ɂ���ė��Ă�ꂽ�����ł���C���i�̕ω��ɑ��锄��i���v�j�y�у}�[�P�b�g�V�F�A�̔����͈��ł͂Ȃ���̋��ܓ_�����ܐ��ł���Ƃ�����̂ł���BGutenberg �́C�}�S�̂悤�ɁC��d���܉��i�����Ȑ��idoubly-kinked price response curve�j�ŃO�[�e���x���O������`���Ă���B
�}�S�̂悤�ɁC�O�[�e���x���O�����ł͒����Ɋɂ₩�ȌX���������C���[���}�ȌX�������ƍl����B���̒��������̌X�����ɂ₩�Ȕ͈͂́C�Ɛ�I�͈́imonopolistic interval�j�ƌĂ��B�������C�{�_���ł́C�Ɛ�I�͈͉͂��i�ω��ɂ�锄��i���v�j�̊��x���Ⴍ�C���̑O��ł͔���i���v�j���}�ɉ��i�ɕq���ɂȂ�5�j���Ƃ���C�Ɛ�I�͈͂��u�ቿ�i���x�̈�v�ƌĂԁB�Ȃ��C�O�[�e���x���O�����ł́C����҂����i�ɑ��āC�\���Ȓm���������Ă��邱�Ƃ����肵�Ă��邽�߁C�ቿ�i�ł͕i�����Ⴂ�Ɗ����w������������Ƃ����͐����Ȃ��Ƃ����O���u���B���̒ቿ�i���x�̈悪�`������闝�R�́C�ȉ��̒ʂ�ł���6�j�B
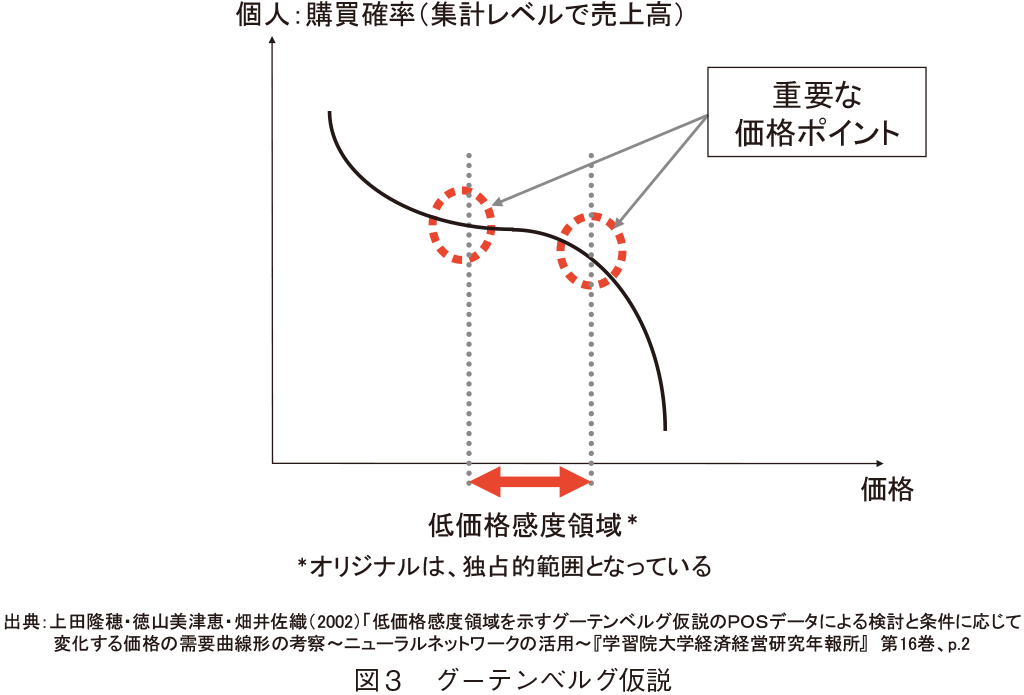
��Ƃ����u�����h�̒l�i���������ꍇ�C���u�����h���w�����Ă�������҂͒ቿ�i�тɂ����đ��u�����h���玩�u�����h�ւ̃X�C�b�`���O�ɂ���ē�������p�Ƒ��u�����h���玩�u�����h�ւ̃X�C�b�`���O�E�R�X�g���r���āC���u�����h�ւ̃X�C�b�`���O�E�R�X�g���x�������y5�Łz���Ȃ����u�����h���w�����������������p��������ꍇ�ɃX�C�b�`����B���̂��Ƃɂ��C���u�����h�̏��i���i��������z�ȉ��ɂ����ꍇ�i�}�S���ia�j���ቿ�i�j�C�̔�������������ƍl����B
�܂��C���u�����h�̉��i���グ���ꍇ�C���u�����h���w�����Ă�������҂́C���u�����h�̃X�C�b�`���O�E�R�X�g���x�����Ă��Ȃ����u�����h���w�����������������p����ꍇ�ɑ��u�����h�փX�C�b�`���O����ƍl���Ă���B����ɂ��C���u�����h�̏��i�̉��i��������z����Ɓi�}�S���ib�j��荂���i�j�C�̔������}���ɒቺ����ƍl����B
�����͈͓̔��i�}�S���ia�j����ib�j�͈͓̔��j�ɂ����ẮC���u�����h���w�����Ă�������҂̓X�C�b�`���O�E�R�X�g�ɂ�葼�u�����h�ւ̈ڍs���s��Ȃ����߁C���u�����h�̉��i�ݒ�ɂ����ēƐ��ԂƓ��l�̉��i������s�����Ƃ��\�ƂȂ�B

����܂ŃO�[�e���x���O���������グ�������͏��Ȃ����C�O�[�e���x���O�����ɏ]�����i�̎��v�Ȑ��̑��݂͎�������Ă���ie.g.,Simon1989; ��c1999�j�B�������C����������ł݂̂ł������̑��݂����o����Ȃ������ie.g., ��c�E���R�E����2002; ����2008�j�B���̂��߁C�{�����ł́CID-POS �f�[�^���g���C�l���Ƃ̉��i���x�ŃO���[�v�������s���C�O�[�e���x���O�Ȑ��̏o�������o�����Ƃ���ڂ̖ړI�Ƃ���B����͏W�v���x���f�[�^�ł���POS �f�[�^�ł͂Ȃ����Ȃ��������Ƃł���B���̍ہC����҂̉��i���x�O���[�v�ʂł��̃O�[�e���x���O�Ȑ��`���ǂ̂悤�ɕω����邩����������B
�y6�Łz�܂��C�ቿ�i���x�̈悪���݂���Ȃ�C�ǂ��܂ł̍����i������҂ɒ�R���Ȃ���e����邩�����炩�ɂȂ�B����́C�ቿ�i���x�̈�̉E�[�Ŏ������B���̏��́C���u�����h�̃f�B�X�J�E���g�ƒl�グ�������̉��i�R���g���[���ŗ��v�z�������s���ۂɏ\���Ӌ`��������ł��낤�B�ቿ�i���x�̈�̕��Ɋւ��錤���Ƃ��āC�ƈ�i2008�j�́C�u�����h�E���C�����e�B�������ƌv�͂��L���ቿ�i���x�̈�����X�������邱�Ƃ������Ă���B�������C����҂̉��i���x���C�ቿ�i���x�̈�̕��ɉe����^���邩�ǂ����Ɋւ��錤���͌�������Ȃ��B����āC�{�����ł́C����҂̏��i�ɑ��鉿�i���x�ɒ��ڂ��C���v�ő剻�ݏo���i�Œ�j���i�|�C���g�i���i�|���j�ɂ��Č������s�����Ƃ��ڂ̖ړI�Ƃ���B
�O�[�e���x���O���������グ�������͏��Ȃ����C���̑��݂��������錤���܂��C����������掦����B
H1�D ���i�̎��v�Ȑ��̓O�[�e���x���O�Ȑ��̌X���������B
H2�D ����҂̏��i�ɑ��鉿�i���x���Ⴂ�قǁC�ቿ�i���x�̈�̕��͂��L���Ȃ�B
H3�D ����҂̏��i�ɑ��鉿�i���x�������قǁC�ቿ�i���x�̈�̕��͋����C�̈�O�̌X�����傫���Ȃ�B
�ቿ�i���x�̈悪�`������闝�R�Ƃ��āC�X�C�b�`���O�E�R�X�g�����������Ő�������Ă���B�{�����ł́C�u�X�C�b�`���O�E�R�X�g�͉��i�e�͐��ƊW���Ă���C�X�C�b�`���O�E�R�X�g�������Ɖ��i�e�͐����Ⴍ�Ȃ�C��������҂͉��i�����܂�C�ɂ��Ȃ��B���ɃX�C�b�`���O�E�R�X�g���Ⴂ�Ɖ��i�e�͐��������Ȃ�C��������҂͉��i�ɑ��ĕq���ɂȂ邱�Ɓv��z�肵�Ă���B
�܂��C�ቿ�i���x�̈悪���炩�ɂȂ邱�Ƃő����̗��v�������炷���i�ݒ肪�\�ƂȂ邱�Ƃ���сC���Ɏ���܂Ń��f���̒莮�����\���ł��Ă��Ȃ����߁C�{�_���ł͌ʃu�����h�ɂ����āw���v�z�ő剻�ݏo�����i�|�C���g�̐���x�������ۑ�Ƃ���B
�W�v���x���f�[�^��POS �f�[�^�̏ꍇ�C���i���x�̈قȂ�ڋq�����݂���B���̂��߁C�f�[�^�͔�W�v���x���C�����l���x���̃f�[�^�ł���ID-POS �f�[�^��p���Čڋq�����i���x�̍���ŃO���[�v�����C���������P�C�Q�C�R����������B
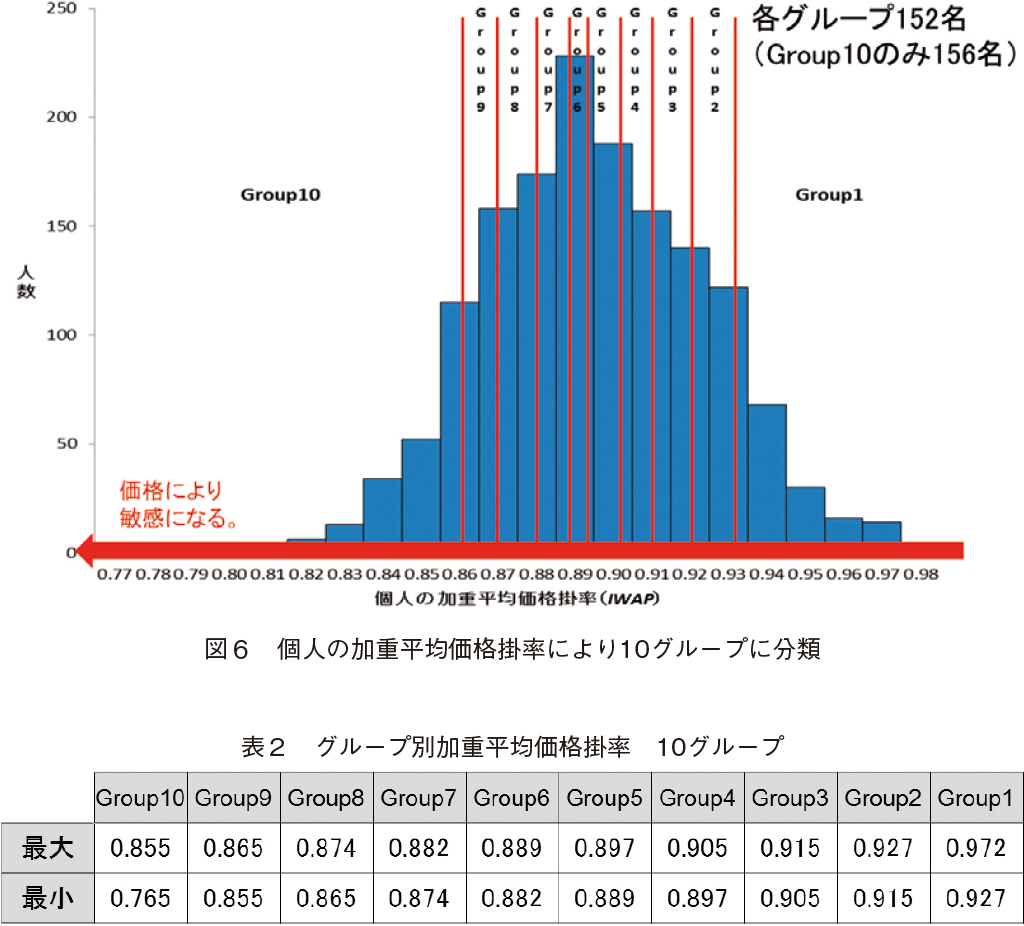
�{�����ł́C�����J�e�S���[�S�̂Ƌ����J�e�S���[�̒��Ŕ��㐔�ʂ��ł������u�����h��Ώۂɕ��͂��s���B�܂��́C�J�e�S���[�S�̂̃f�[�^���g���C���i���x�ɂ���ĕ��ނ����O���[�v���Ƃ̉��i�̎��v�Ȑ����������邱�Ƃɂ��C�����P�C�Q�C�R����������B�������C�\�P�̒ʏ퉿�i���[�J�[��]�������i�j�������Ƃ���C�����̉��i�т�200�~�`400�~�O��ƕ��L�����߁C���i�ʂɑ������������N���A�Ɍ������ʂ��ł邱�Ƃ����炩�ɂȂ����B���̂��߁C�����J�e�S���[�S�̂ŃO�[�e���x���O�Ȑ��̌`�����邩�ǂ����̊T�ς��s������ŁC���㐔�ʂ��ł������ʃu�����h�̃f�[�^���g���C�����P�C�Q�C�R�̂��ڍׂȌ������s���C�����ۑ�ɂ����g�ނ��Ƃɂ���B
�T�D�����J�e�S���[���̂�ΏۂƂ�������
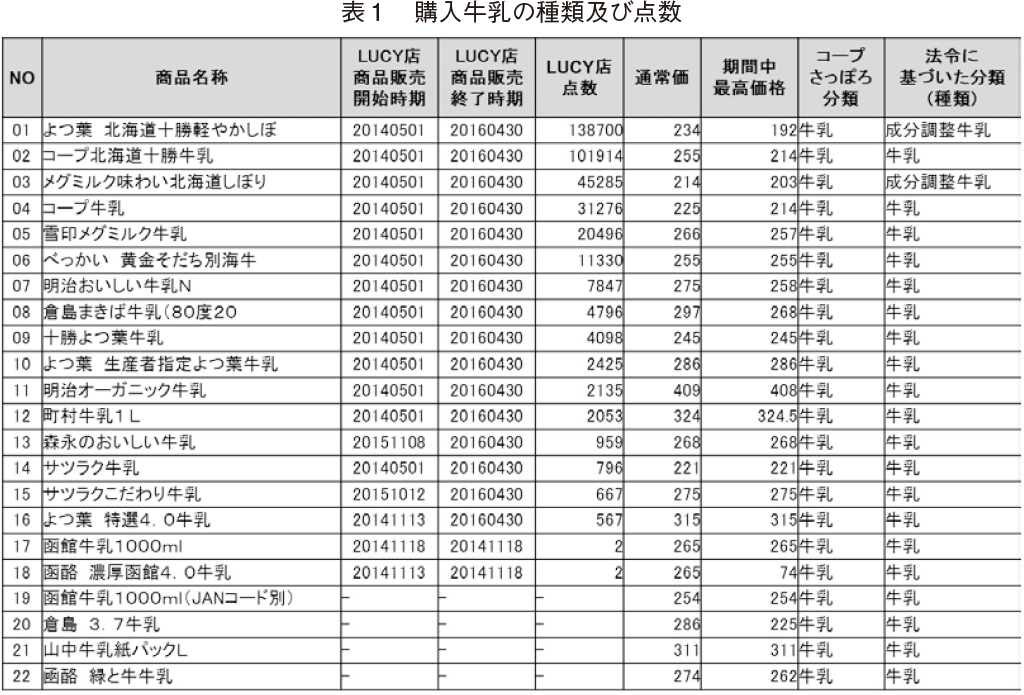
�R�[�v�����ۂ������������ID-POS �f�[�^�𗘗p���C�Ώې��i�������Ƃ����B���̍ہC�������������͊܂߂邪�C�ᎉ�b�����C�����b�����͊܂߂Ȃ����Ƃɂ����B�ΏۓX�܂̓R�[�v�����ۂ�̑�^�X�ł���LUCY �X�Ƃ������CID-POS �f�[�^�䂦�C�l�̓��肪�\�Ȃ��ƂƎԒ��S�Љ�œX�܂̕��s���p���l�����邽�߁C�R�[�v�����ۂ�LUCY �X���p�ڋq�́C���ӂTkm �ȓ��̃R�[�v�����ۂ�T�X�܁i���������X�C�Ђ胖�u�X�C�쉺�X�C�����X�C�{���X�j�ł̍w���ʂ��l���ɓ��ꂽ�B2014�N�T���P���`2016�N�S��30���̂Q�N�Ԃ̓��ʃf�[�^�ɂ����āC�����PL �p�b�N��52�T�ȏ�w�����Ă��邱�Ƃ������Ɍڋq�𒊏o�����Ƃ���C1,524�l�ł������B�Ȃ��C�����̕��ϔ�����50�~�ȉ��̏ꍇ�C�Ɩ��p�Ƒz�肳���P����10�{�ȏ�w�����Ă���ꍇ�C����уR�[�v�����ۂ�LUCY �X�Ŕ���̂Ȃ����t�i2014/7/25�C2015/4/14�`16�j�̏ꍇ�C�����̃f�[�^�͏����ĕ��͂��s�����B
�\�P�̓R�[�v�����ۂ�LUCY �X�ł̍w�������̎�ދy�ѓ_���Ȃǂ��܂Ƃ߂����̂ł���B
�T�|�P�D���͂̎菇
���͈͂ȉ��̎菇�ōs�����B
���D �w���҂����i���x�̑傫����ŃO���[�v�ɕ���
���D �O���[�v���ƂɁC�Q�N�Ԃ̔��㐔�ʉ��d���ω��i�|���Ɣ�����̊W���O���t�����C�O�[�e���x���O�Ȑ��������邩�C���i���x�������قǒቿ�i���x�̈�̕����������C�y8�Łz�����ċȐ��̌X�����}�X�ɂȂ邩������
�T�|�Q�D�����J�e�S���[�S�̂�ΏۂƂ�������
�i�P�j�w���҂����i���x�̑傫������ɃO���[�v�ɕ���
�{���͂ł͉��i���x�̑���̎w�W�Ƃ��āC�l���Ƃ̍w�����ɂ����鉿�i�|����p����B���i�|���͊��Ԓ��i�����ł͂Q�N�ԁj�ō����i�őΏۓ��̍w�����i�����������̂Ƃ��C�ǂ̂��炢�̉��i�i���j�ŋ����������������i�}�T���Q�Ɓj�B
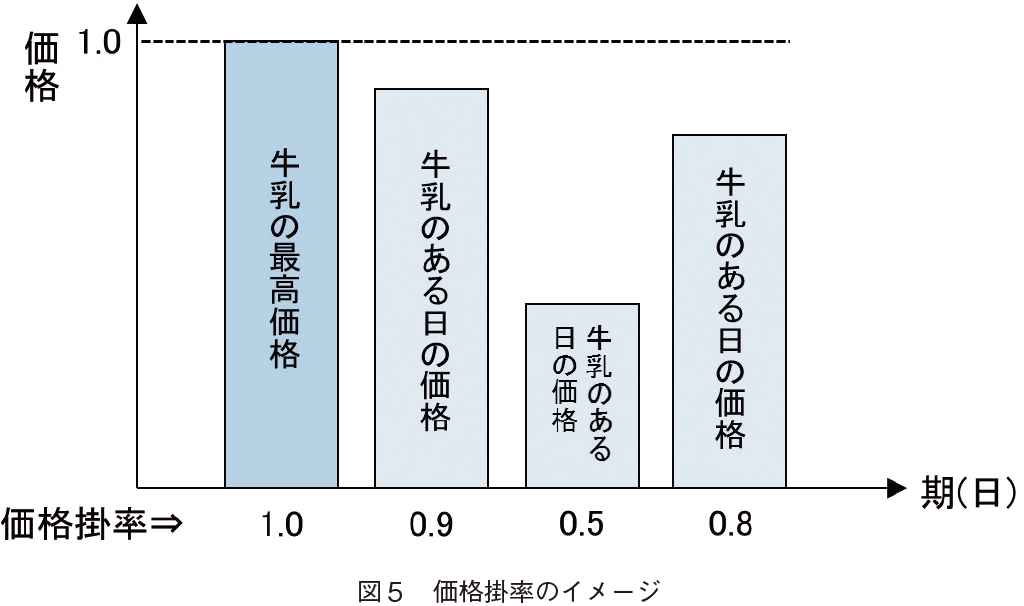
�܂��C������ނ̋������Ă��邱�Ƃ��������߁C�����̔��㐔�ʂɂ��l�̉��d���ω��i�|���iIWAP�FIndividual Weighted Average Price rate�j�����߂�B�l�̉��d���ω��i�|���Ƃ́C�l���Ƃɖ����C��ނ��ƂɁC���i�|�����v�Z���C�Q�N�Ԃ̉��d���ς����߂����̂ł���B
���Ƃ��C��l�ڂ�
�P���ځF���iA�@����_��n1A1�@���ϔ���pA1�~�C
���iB�@����_��n1B1�@���ϔ���pB1�~�ōw��
�Q���ځF���iA�@����_��n1A2�@���ϔ���pA2�~�ōw��
���Ԓ��ō����i�F���iA �� pA �~�C���iB �� pB �~
���v�w�����Fn1�� n1A1+ n1B1+n1A2
�̏ꍇ�́C
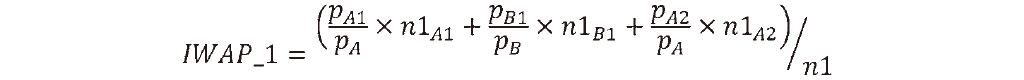
��ʂɁC���i��Z ��ށC������nd ���C N �l�ڂ̍��v�w������nN �Ƃ���ƁC
�y9�Łz
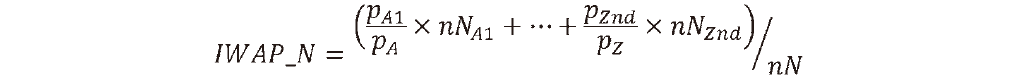
�����āC�Ώۂ�1,524�l���l�̉��d���ω��i�|���������i�����i���x���Ⴂ�j���Ƀ\�[�g���C�f�V�����͂̂悤�ɑS�l����10��������B
�i�Q�j�Q�N�Ԃ̉��d���ω��i�|��
�O���[�v���ƂɁC���t���Ƃ̉��d���ω��i�|�������߂����̂���ʃO���[�v���d���ω��i�|���iDGWAP�FDaily Group Weighted Average Price rate�j�Ƃ���B
���Ƃ��C�O���[�v�P��2014/05/01�ɂ��Ă̍w�����Q���������ꍇ�C
�l01����F���iA�@����_��nA01�@���ϔ���pA01�~�C
���iB�@����_��nB01�@���ϔ���pB01�~�ōw��
�y10�Łz�l02����F���iA�@����_��nA02�@���ϔ���pA01�~�ōw��
���Ԓ��ō����i�F���iA �� pA �~�C���iB �� pB �~
���v�w�����Fn20140501�� nA01+nB01+nA02
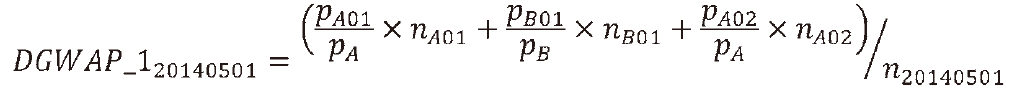
��ʂɁC���i��Z ��ށC�O���[�vG �̂���N�����ɂ����čw�������̂�N ���C����N�����̍��v�w������n �N�����Ƃ���ƁC
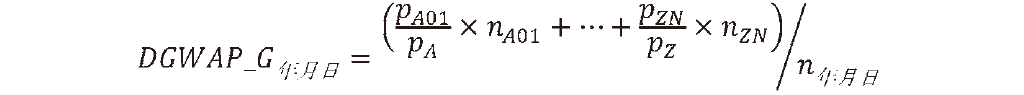
�����āC���鉿�i�iDGWAP�j�Ŕ�������������Ɣ�����������Ȃ�̂ŁC�����̉e����r������K�v������B���̂��߁C�Q�N�Ԃ�DGWAP ���l�̌ܓ��ɂ�菬����Q�ʂ܂ŋ��߁CDGWAP �̒l���Ƃ̓����𐔂���B����DGWAP �̒l�ł̔���������̓����Ŋ���C��������������iDASV�FDaily Adjusted Sales Volume�j�Ƃ���B
�i�R�j�S�́i�O���[�v���v�j�ŊO��
��L�̃f�[�^��艿�i�̎��v�Ȑ���`���B�}�V���C�S�́i�O���[�v���v�j�ł̓��ʃO���[�v���d���ω��i�|���ƒ���������̊W�����Ă݂�B���ϓI�ɂł͂��邪�C���炩�ɒ������͓��Ă͂܂肪�ǂ�������B�}�V���}�̉��i�|�����S���Ԃ�10���ȏ�o���������̂��̗p�������B���l�I�Ȍ��̓u�����h���x���Ŏ��{���邱�Ƃɂ���B
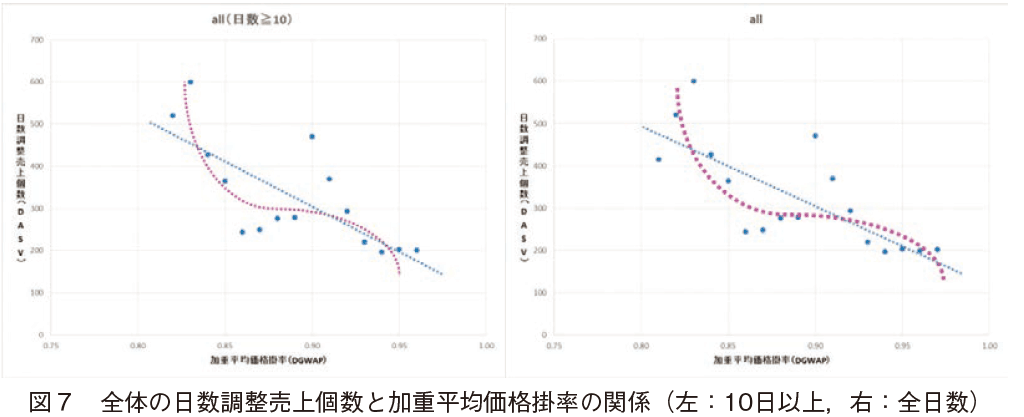
�i�S�j�O���[�v���ƂɌ���
���i���x�̈قȂ�10�O���[�v�ʼn��i�Ɣ��㐔�ʂƂ̊W���݂�BGroup1���ł����i���x�̒Ⴂ�O���[�v�i���l�����ɔ��������C�ō����i�߂��Ŕ����l�X�j�ł���CGroup10���ł����i�y11�Łz���x�̍����O���[�v�i���l�����ɓ��ɔ������C�ō����i�߂��ł͔���Ȃ��l�X�j�ł���B�}�W���Q�Ƃ��ꂽ���B���̐}�́C�O���[�v���Ƃ̓�������������iDASV�j�Ɖ��d���ω��i�|���iDGWAP�j�̊W���猩�����i�̎��v�Ȑ��ł���B�X�������邽�߂ɃO�[�e���x���O�Ȑ��̌`����Ƃ�⏕����`���Ă݂��Ƃ���CGroup10�ɂȂ�قnjX�����傫���Ȃ�C�ቿ�i���x�̈�̕��������Ȃ邱�Ƃ��C���F���x���ł͂��邪�킩��B����͐}�X������Ƃ킩��₷���B
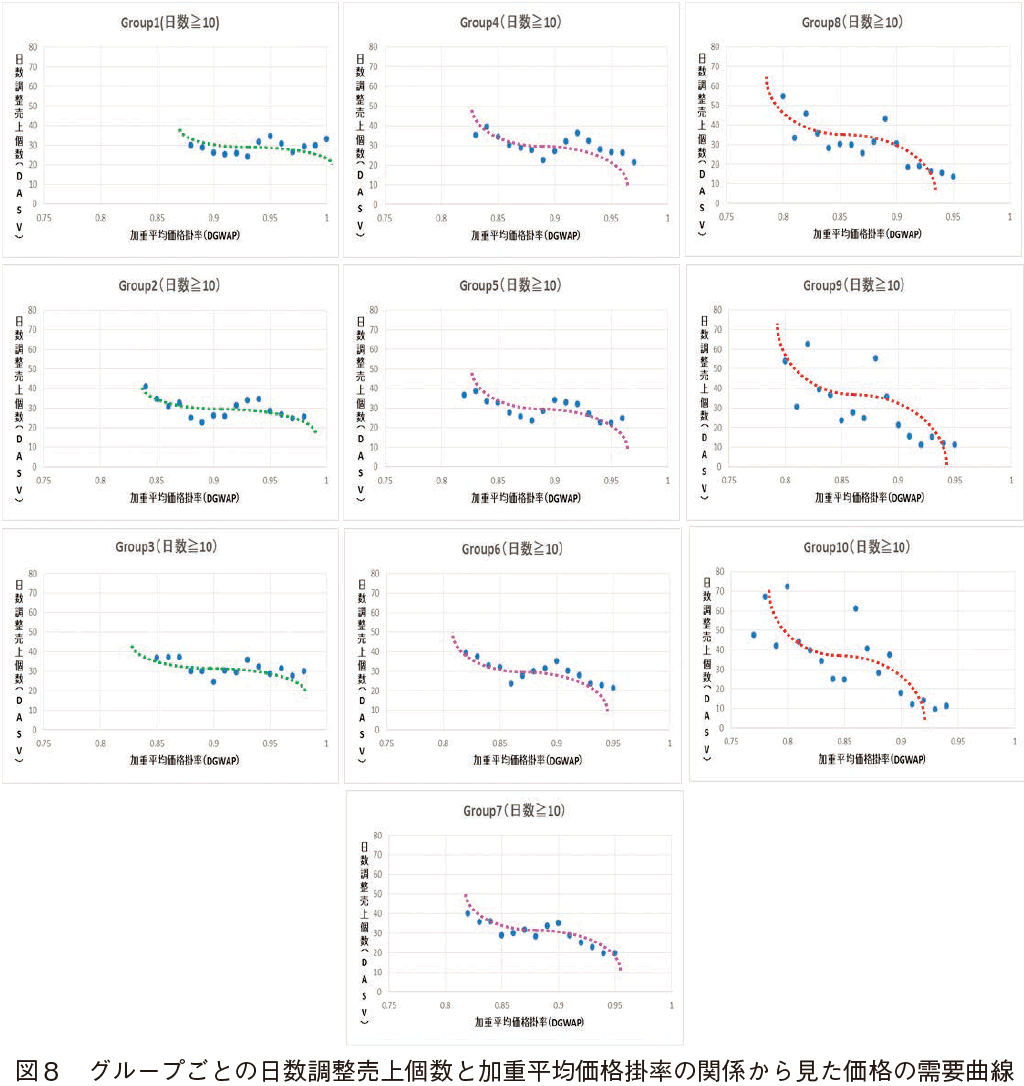
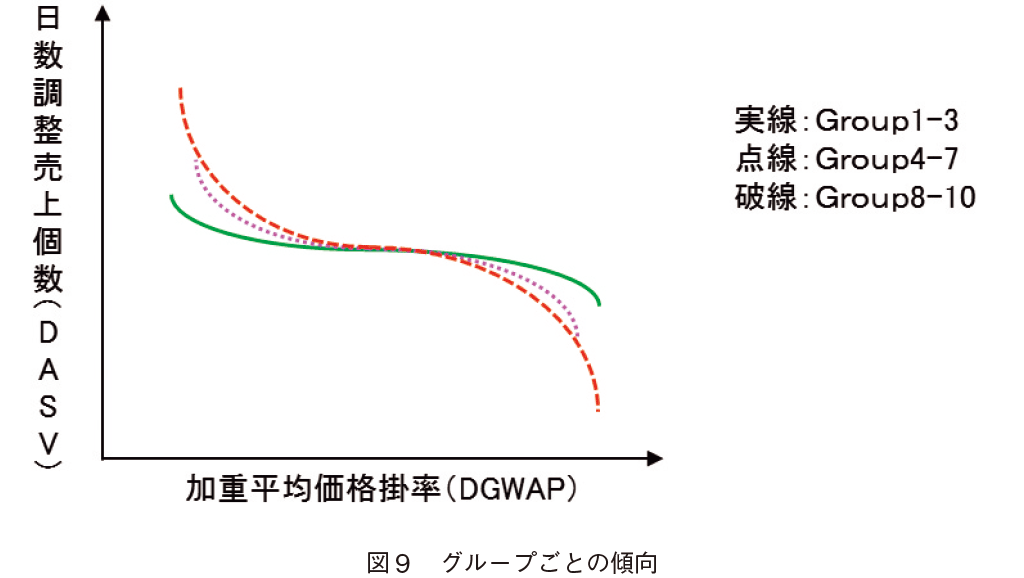
�T�|�R�D���ʂ̍l�@
�J�e�S���[�S�̂�ΏۂƂ������ʂł́C�S�̂ł��C���i���x�ʃO���[�v�ł��O�[�e���x���O�Ȑ��͑��݂��Ă���悤�ł���C���ɉ��i���x�������O���[�v�ŃO�[�e���x���O�Ȑ��͌����ł������B
���ʓI�ɁC�J�e�S���[�S�̂�Ώۂɂ����ꍇ�C�S�͂̉����P�C�Q�C�R�͎��F���x���̊ϓ_���炨���悻�m�F���ꂽ�B�������C���i�ݒ�̈قȂ鋍�����������Ă��邽�߁C�O�[�e���x���O�Ȑ��͏o�����ɂ����\���������ƍl������B�̂ɁC�ł�����Ă���ʃu�����h�Ŏ��݂�C�O�[�e���x���O�Ȑ�������ɃN���A�ɏo������̂ł͂Ȃ����Ƃ̍l���̂��ƂɎ��͂ł͌ʃu�����h�ɂ��Č������C����̓I�Ȑ��l�I�������{����B
�U�D�����J�e�S���[�ł̍ő唄�㐔�ʃu�����h��ΏۂƂ�������
�{�͂ł́C�ʃu�����h�ɂ��đO�o�̉����P�C�Q�C�R�̌�������ь����ۑ�̍l�@���s���B
���p�f�[�^�́C�T�͂Ɠ��l��ID-POS �f�[�^�𗘗p�����B����̕��͂ł́C2014�N�T���P���`2016�N�S��30���̂Q�N�Ԃɂ����āC���㐔�ʂ��ł��傫���u�����h�iNo1�u�����h�j�̂�t�k�C���\���y�₩���ڂ��Ώۃu�����h�Ƃ����B���͑Ώێ҂́C��t�k�C���\���y�₩���ڂ�PL �p�b�N���Q�N�Ԃ�52�T�ȏ�w�����Ă��邱�Ƃ������Ɍڋq�𒊏o�����Ƃ���C315�l�ł������B�Ȃ��C�R�[�v�����ۂ�LUCY �X�Ŕ���̂Ȃ����t�i118���j�̃f�[�^�͏����ĕ��͂��s���B
�Ȃ��C�����u�����h�Ƃ��āC���㐔�ʂ���Ԗڂɑ傫���u�����h�iNo2�u�����h�j�̃R�[�v�k�C���\��������ݒ肵���B�Ώێ�315���ɑ���No2�u�����h�̃R�[�v�k�C���\�������̔��y13�Łz����т́CNo1�u�����h�̔������613���̂���426���ł������B
�U�|�P�D���͂̎菇
���͂̎菇�Ƃ��ẮC�ȉ��̒ʂ�̎菇�ōs�����B
���D �w���҂����i���x�̑傫������ɃO���[�v�ɕ��ނ��C�w���ґS�̂ƃO���[�v���Ƃɉ��i�̎��v�Ȑ��`������
���D �w���ґS�̂ƃO���[�v���ƂɁC�O�[�e���x���O�Ȑ��Ɛ��`��A�Ȑ��̓��Ă͂܂����r
���D �w���ґS�̂ƃO���[�v���ƂɁCSPSS Modeler ��p���C�j���[�����l�b�g���[�N�ɂ���ăf�[�^���烂�f���𐄒�C������̗\���l�𐄒肵�C�v���b�g
���D ���㐔��No1�u�����h��No2�u�����h�̉��d���ω��i�|���iDGWAP�j�ȊO�̉e���ϐ��͎��ۂ̒l�𐄒胂�f���ɓ��}���C���㐔��No1�u�����h�̉��d���ω��i�|���iDGWAP�j��0.01���݂ŕω������C���㐔��No2�u�����h�̉��d���ω��i�|���iDGWAP�j�͇@���ۂ̒l����}�C�A���Ԓ��ő�l�ɌŒ�C�B���Ԓ��ŏ��l�ɌŒ肵�āC������̗\���l�𐄒肵�C�v���b�g
���D ������̗\���l����C���v�z�̃V�~�����[�V�������s���C�ō����v�z�ݏo�����i�|���i�Œ�j�𐄒�
�U�|�Q�D�����J�e�S���[�ł̍ő唄�㐔�ʃu�����h��ΏۂƂ�������
�i�P�j �w���҂����i���x�̑傫������ɃO���[�v�ɕ��ނ��C�Ώۃu�����h�Ɋւ��āC�S�̂ƃO���[�v���Ƃɉ��i�̎��v�Ȑ�������
���i���x�ʂ̉��i�̎��v�Ȑ������o�����߂ɁC�T�͂Ɠ����菇�ɏ]���āC�l�̉��d���ω��i�|���iIWAP�j���Z�o�����B�}10�͑Ώێ҂̌l�̉��d���ω��i�|���iIWAP�j�̕��z�}�ŁC�ő�l��0.92�C�ŏ��l��0.78�ł������B�l�̉��d���ω��i�|���iIWAP�j1.00�́C���Ԓ��ō����i��192�~�������B
�y14�Łz
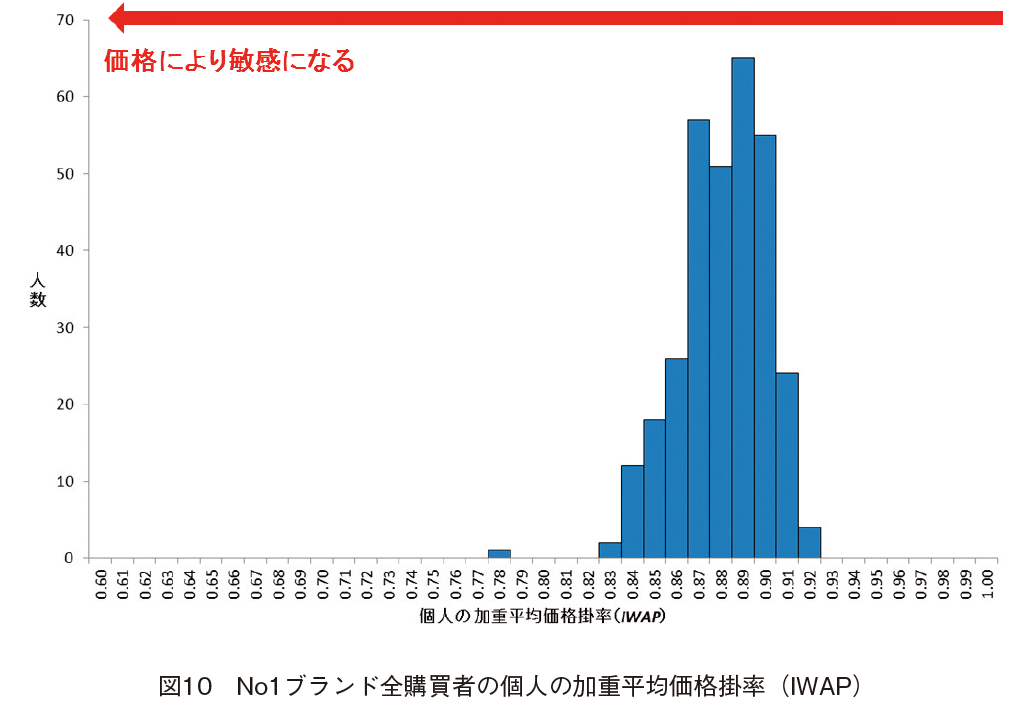
�T�͓��l�̎菇�ɏ]���C�f�V�����͂̂悤�ɑΏۂ�315�l���l�̉��d���ω��i�|���iIWAP�j�������i�����i���x���Ⴂ�j���Ƀ\�[�g���C10�����ɂ����Ƃ���CGroup1����Group10�ɂȂ�ɂ�āC���i�ɕq���ƂȂ����B
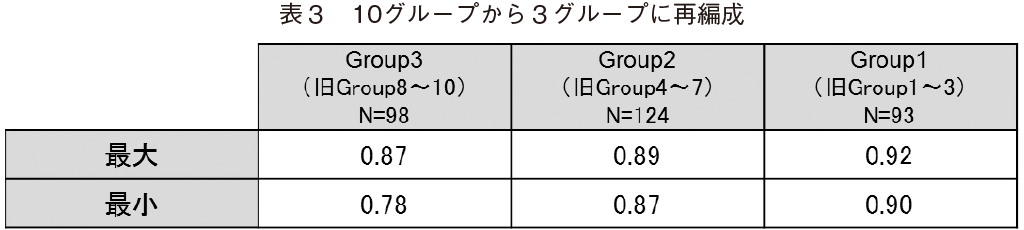
�������C�j���[�����l�b�g���[�N�ɂ�郂�f������ɂ́C�T���v�������ɒ[�ɕs�����Ă��邽�߁C10�O���[�v����R�O���[�v�ɍĕҐ������i�\�R�j�B�e�O���[�v�̌l�̉��d���ω��i�|���iIWAP�j�ő�l�ƍŏ��l�Ɋւ��ẮC�R�O���[�v�̒��ōł����i���x���ႢGroup1�ł͍ő�l��0.92�C�ŏ��l��0.90�C���i���x�������x��Group2�ł͍ő�l��0.89�C�ŏ��l��0.87�C�ł����i���x���������i�ɕq����Group3�ł͍ő�l��0.87�C�ŏ��l��0.78�ł������B
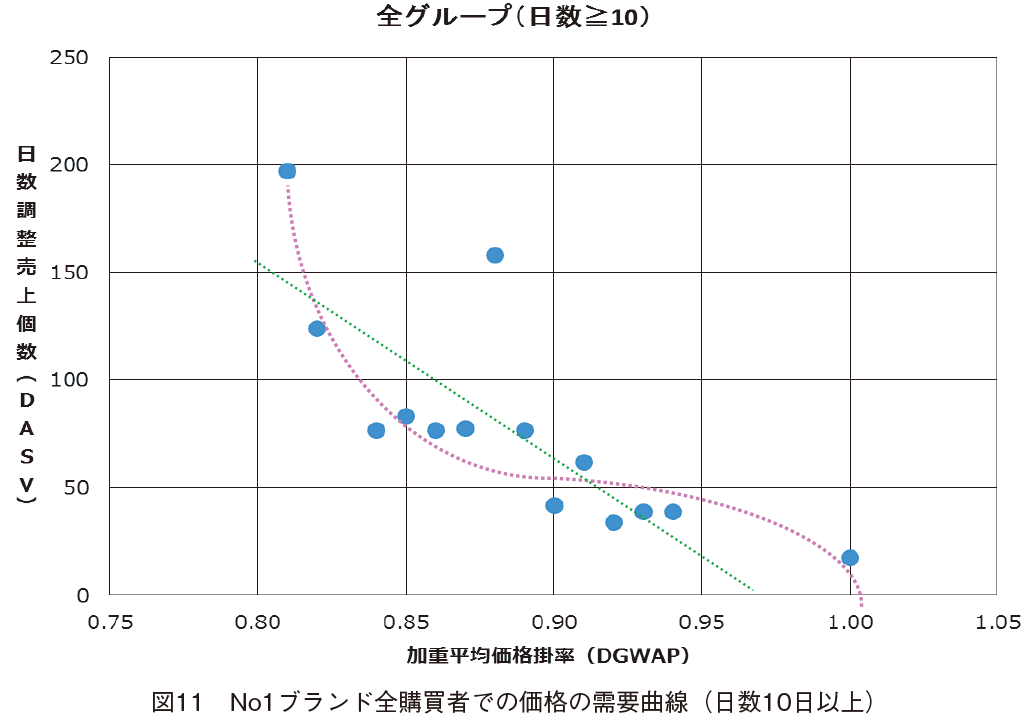
No1�u�����h�̂�t�k�C���\���y�₩���ڂ�ɂ��āC�S�̂ƃO���[�v���Ƃ̓�������������iDASV�j�Ɖ��d���ω��i�|���iDGWAP�j�̊W�́C�}11�C12�C13�C14�������Ƃ����y15�Łz�ł���B�����̐}�ɂ́C�����P�C�Q�C�R���������邽�߁C�q���[���X�e�B�b�N�ȃO�[�e���x���O�Ȑ��^�⏕����`���Ă���B����ɁC���`��A�Ȑ����`���C�O�[�e���x���O�Ȑ��Ƃ̓��Ă͂܂��̐��l��r���s���B�Ȃ��C���i�̎��v�Ȑ��`��c�����邽�߂ɁC����Ă��������10�������̋ɏ��Ȃ����d���ω��i�|���iDGWAP�j�͏����Ă���B
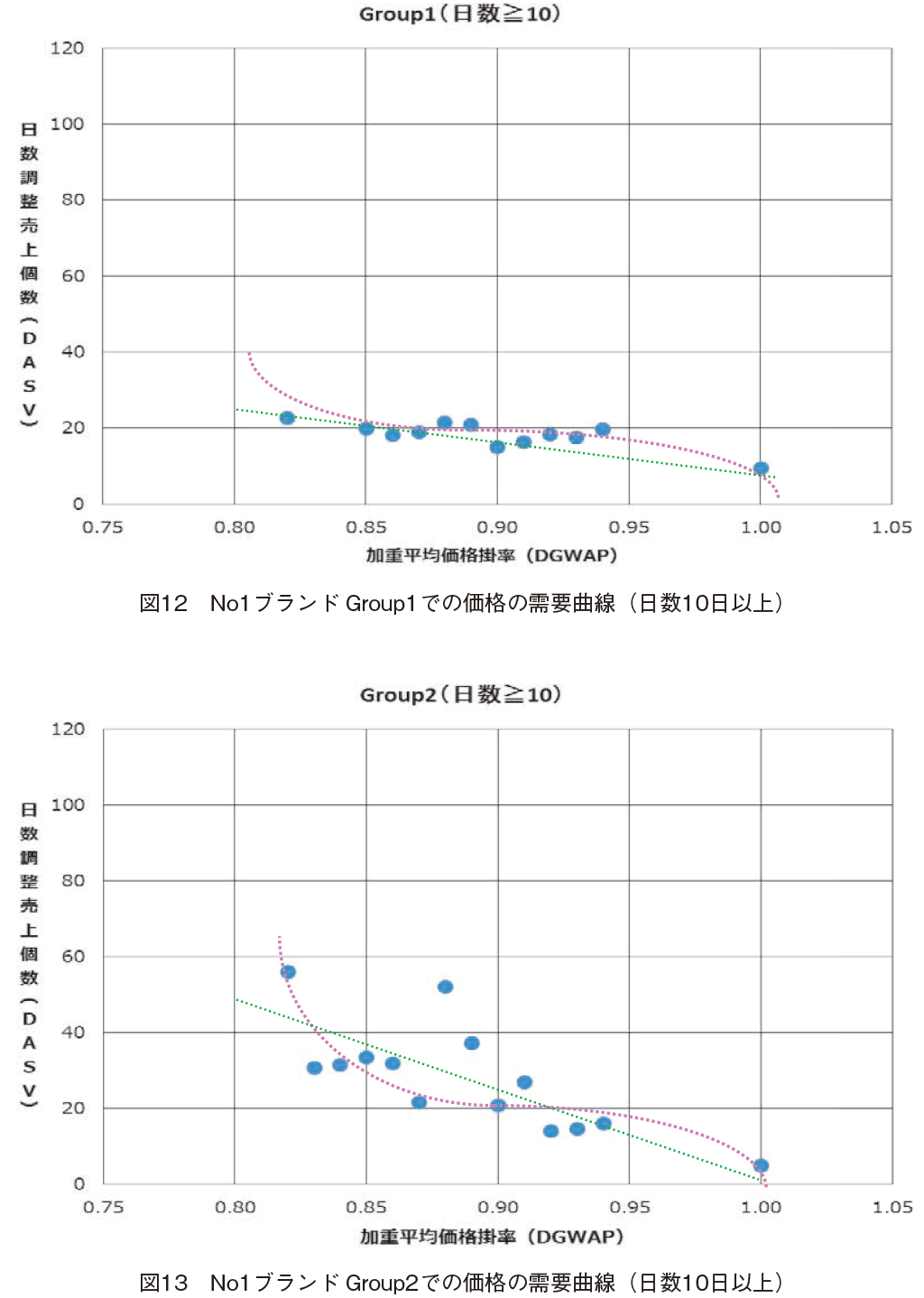
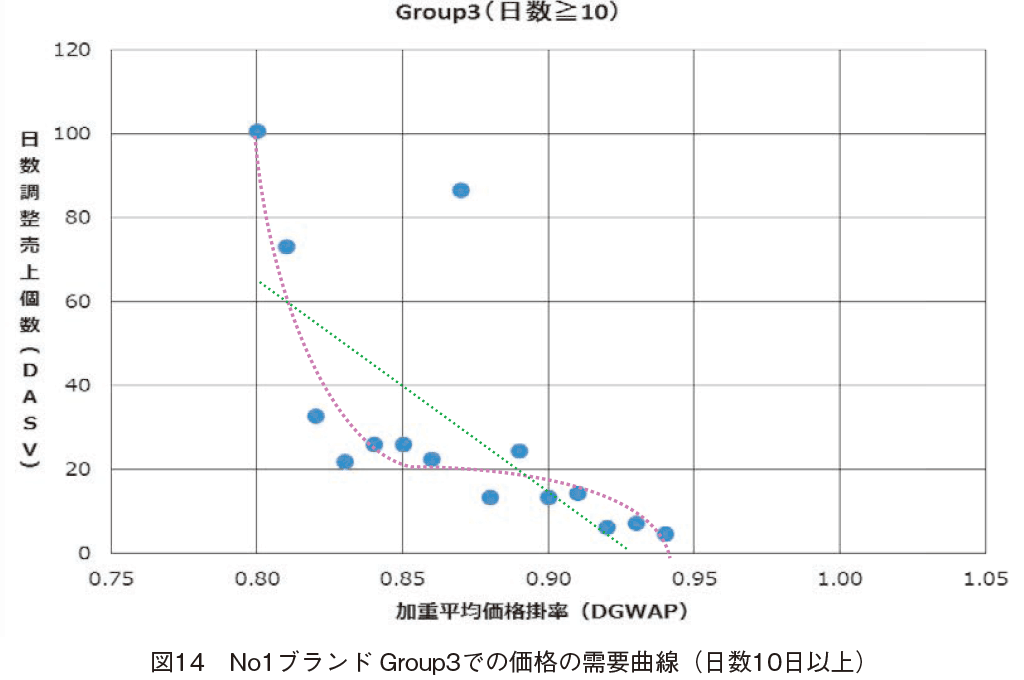
�ʃu�����h��ΏۂƂ������ʂł́C�S�̂ł��C�ʉ��i���x�O���[�v�ł��O�[�e���x���O�Ȑ��͎��F���x���ő��݂��邱�Ƃ����������B���i���x���Ⴍ�Ȃ�Group3, 2, 1�̏��ɒቿ�i���x�̈�̕����L���Ȃ������ƁC����ɉ��i���x�������Ȃ�Group1, 2, 3�̏��ɁC�ቿ�i���x�̈�O�̌X�����傫���Ȃ邱�Ƃ��킩�����B
���ʓI�ɁC�ʃu�����h��ΏۂƂ����ꍇ�C�����P�C�Q�C�R�́C���F���x���̊ϓ_����͊m�F���ꂽ�B
�i�Q�j���`��A�Ȑ��Ɠ��Ă͂܂��̐��l��r
�O�[�e���x���O�Ȑ��Ɛ��`��A�Ȑ��̕��ϐ�Ό덷�iMAE�FMean Absolute Error�j���r����B�O�[�e���x���O���v�Ȑ��̕��ϐ�Ό덷�́C�}11�C12�C13�C14����Y ���ɉ����������icm�j�̐�Βl�𑪂�C���ϐ���������߂�B�Pcm ������̓�������������ɒu�������ĕ��ϐ�Ό덷���v�Z�����B
���D No1�u�����h�S�w���҂ł̉��i�̎��v�Ȑ��i����10���ȏ�j
���`��A�̐��莮�́C
y ��747.18�|753.28x
�ƂȂ����B���ϐ�Ό덷�ɂ��Đ��`�����22.62�C�O�[�e���x���O�Ȑ���13.32�ł������B
���D No1�u�����hGroup1�ł̉��i�̎��v�Ȑ��i����10���ȏ�j
���`��A�̐��莮�́C
y ��68.36�|55.86x
�ƂȂ����B���ϐ�Ό덷�ɂ��Đ��`�����1.87�C�O�[�e���x���O�Ȑ���0.67�ł������B
���D No1�u�����hGroup2�ł̉��i�̎��v�Ȑ��i����10���ȏ�j
���`��A�̐��莮�́C
y ��222.98�|219.41x
�ƂȂ����B���ϐ�Ό덷�ɂ��Đ��`�����7.11�C�O�[�e���x���O�Ȑ���5.00�ł������B
���D No1�u�����hGroup3�ł̉��i�̎��v�Ȑ��i����10���ȏ�j
���`��A�̐��莮�́C
y ��429.59�|457.55x
�ƂȂ����B���ϐ�Ό덷�ɂ��Đ��`�����15.69�C�O�[�e���x���O�Ȑ���7.53�ł������B
����āC���ϐ�Ό덷�Ŕ�r�����ꍇ�C�S�̂ł��C�ʉ��i���x�O���[�v�ł��O�[�e���x���O�Ȑ��̕������f���̓��Ă͂܂肪�悩�����B
���߂ŁC�����ۑ�̗��v�ő剻�ݏo�����i�|�C���g�Ɋւ��Č������邪�C�R�O���[�v�ɍĕҐ����Ă��T���v�������s�����Ă��邽�߁CNo1�u�����h�̂�t�k�C���\���y�₩���ڂ�S�̂ł̌������s���B
�i�R�j�j���[�����l�b�g���[�N�ɂ�郂�f���̐���
SPSS ��Modeler �̃j���[�����l�b�g���[�N�𗘗p���āC���㐔�ʐ��胂�f�����܂�����B�����ď]���ϐ��C�Ɨ��ϐ����ȉ��̂悤�ɐݒ肵���B�Ɨ��ϐ��́C����ɉe����^���鉼���I�ȕϐ��Ƃ��đS����29�ϐ��Ƃ��Ă���B
�]���ϐ��F ���ʂ̔�����i�R�[�v�����ۂ�LUCY �X�ł�t�k�C���\���y�₩���ڂ�̔���̂Ȃ����t�f�[�^�͏����j
�Ɨ��ϐ��F No1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j�CNo2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�i�R�[�v�k�C���\�������̔��オ�Ȃ����́C�u1.00�v�Ɛݒ�j�C���X�q���C���_�~�[�i11�ϐ��j�C�j���_�~�[�i�U�ϐ��j�C�N���x�����_�~�[�i��������15���B�������C15�����y�j���C���j���܂��͏j���̂Ƃ��́C���̒��O�̕����j�C�����E�j���i�x���j�_�~�[�C�T�[�r�X�f�[�i�Q�`12���̂P�`�R�����P�C���̑����O�j�C�N���_�~�[�i12/29�`31���P�C���̑����O�j�C�N�n�_�~�[�i1/1�`3���P�C���̑����O�j�C�D�y�̓��ʍō��C���i���j�C�D�y�̓��ʍ~��icm�j�C�D�y�̓��ʍŐ[�ϐ�icm�j�C�D�y�̓��ʍ~���ʁimm�j
�쐬�����S�̃��f���̗\�����x��88.7���C��Ƃ��Đݒ肵�����Ώd�v�x0.02�ȏ�̗\���ϐ���11�ϐ��������B���Ώd�v�x�̍������̂��珇�ɁC���X�q���y0.309�z�i�y�@�z���̐��l�́C�y19�Łz���Ώd�v�x�j�C���j���y0.206�z�CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j�y0.114�z�CNo2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�y0.104�z�C�D�y�~���ʁy0.058�z�C12���y0.052�z�C�D�y�ō��C���y0.043�z�C�D�y�~��y0.037�z�C�N���x�����y0.029�z�C���j���y0.026�z�C�N���y0.022�z�ł������i�j���[�����l�b�g���[�N�ł͓��v�I�L�ӌ���͍s���Ȃ��j�B
���肵�����f������\�������������p���ĎZ�o�������������\��������i�\��DASV�j�Ɖ��d���ω��i�|���iDGWAP�j�̊W�́C�}15�������Ƃ���ł���B���̐}������Ă��������10�������̋ɏ��Ȃ�DGWAP �͏��������̂ŁC���i�̎��v�Ȑ��`��c�����邽�߂ɁC�O�[�e���x���O�Ȑ��^�̃q���[���X�e�B�b�N�ȕ⏕����`���Ă���B
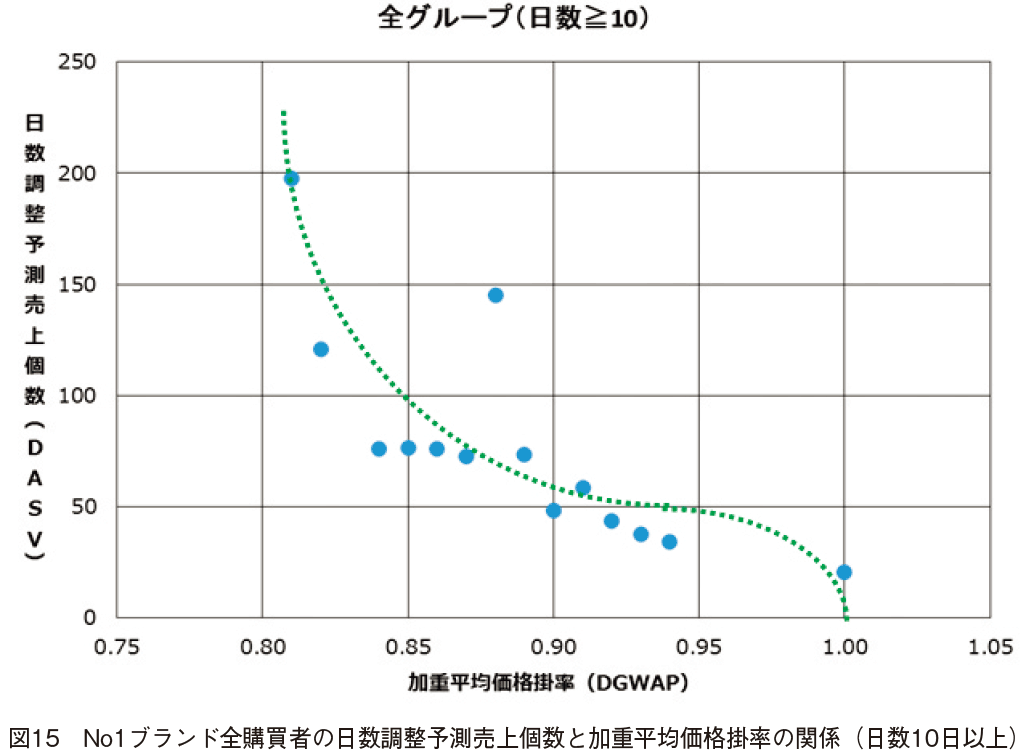
�����l�Ɛ��肵�����f���ɂ��\���l���d�˂��}���C�}16�ł���B�S�̂ł��C�ʉ��i���x�O���[�v�ł��C�قڎ����l�ɋ߂��\���l������ꂽ�B
�y20�Łz
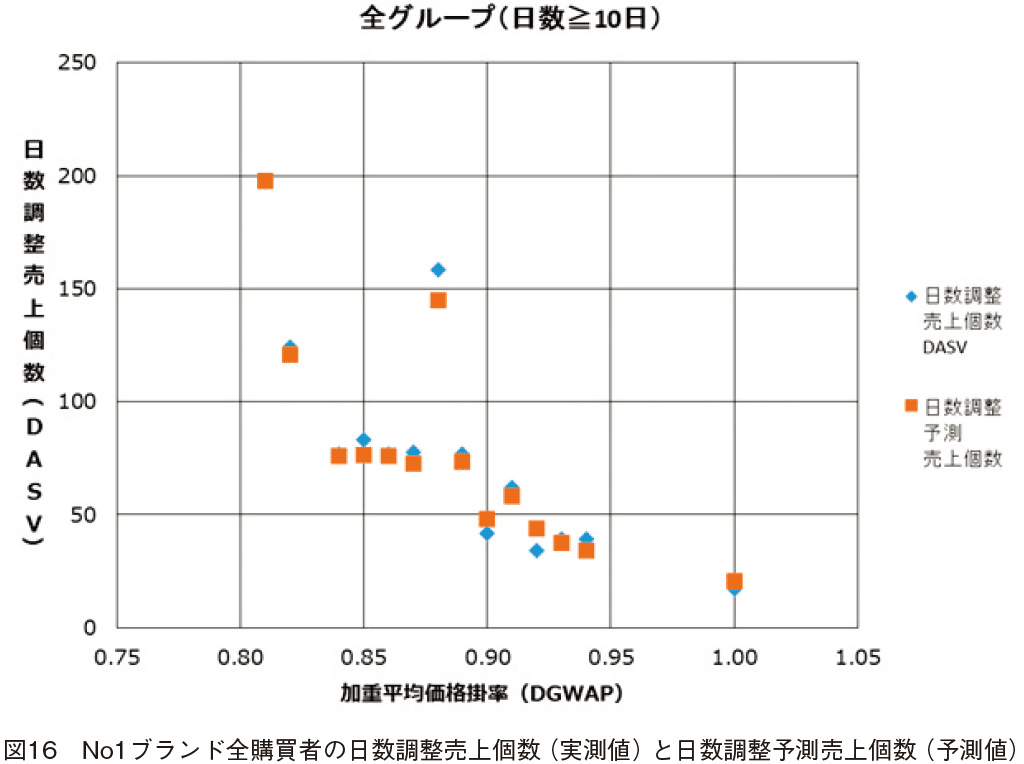
�i�S�j���f�����g�����V�~�����[�V�����̎��{
�쐬�����j���[�����l�b�g���[�N�̃��f�����g�p���CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j��No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�ȊO�̕ϐ��͎����l����}���C������Ƃɗ\����������ǂ̂悤�ɕω����邩�V�~�����[�V�������s�����B�����u�����h�ł���No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�ɂ��ẮC�������R�ݒ肵���B�P�ڂ͎��ۂ̒l�C�Q�ڂ͑Ώۊ��ԂQ�N�ԁi2014�N�T���P���`2016�N�S��30���j�ɂ�������Ԓ��ő�l�i����10���ȏ�j�ɌŒ�C�R�ڂ͊��Ԓ��ŏ��l�i����10���ȏ�j�ɌŒ肷�邱�Ƃł���B�������Ƃɓ��̓f�[�^�𐄒胂�f���ɓK�p���CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j�̒l��0.01���݂Ŏ����l�͈̔͊O���܂߂�0.70�`1.10�͈̔͂ŕω������C���d���ω��i�|���iDGWAP�j���ƂɂQ�N�ԓ����̗\��������𐄒肵���B
���̓f�[�^���Q�l�Ɏ����Ă����ƁC�\�S�ƂT�̂悤�ɂȂ�B�\�S�́CNo2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�����Ԓ��ő�l��1.00�ŌŒ�CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j��0.70�`1.10�͈͓̔���0.70�ŌŒ�C���X�ϐ��͎����l�Ƃ������̓f�[�^�ł���B�\�T�́CNo2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�����Ԓ��ŏ��l��0.83�ŌŒ�CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j��0.70�`1.10�͈̔͂�0.70�ŌŒ�C���X�ϐ��͎����l�y21�Łz�Ƃ������̓f�[�^�ł���B
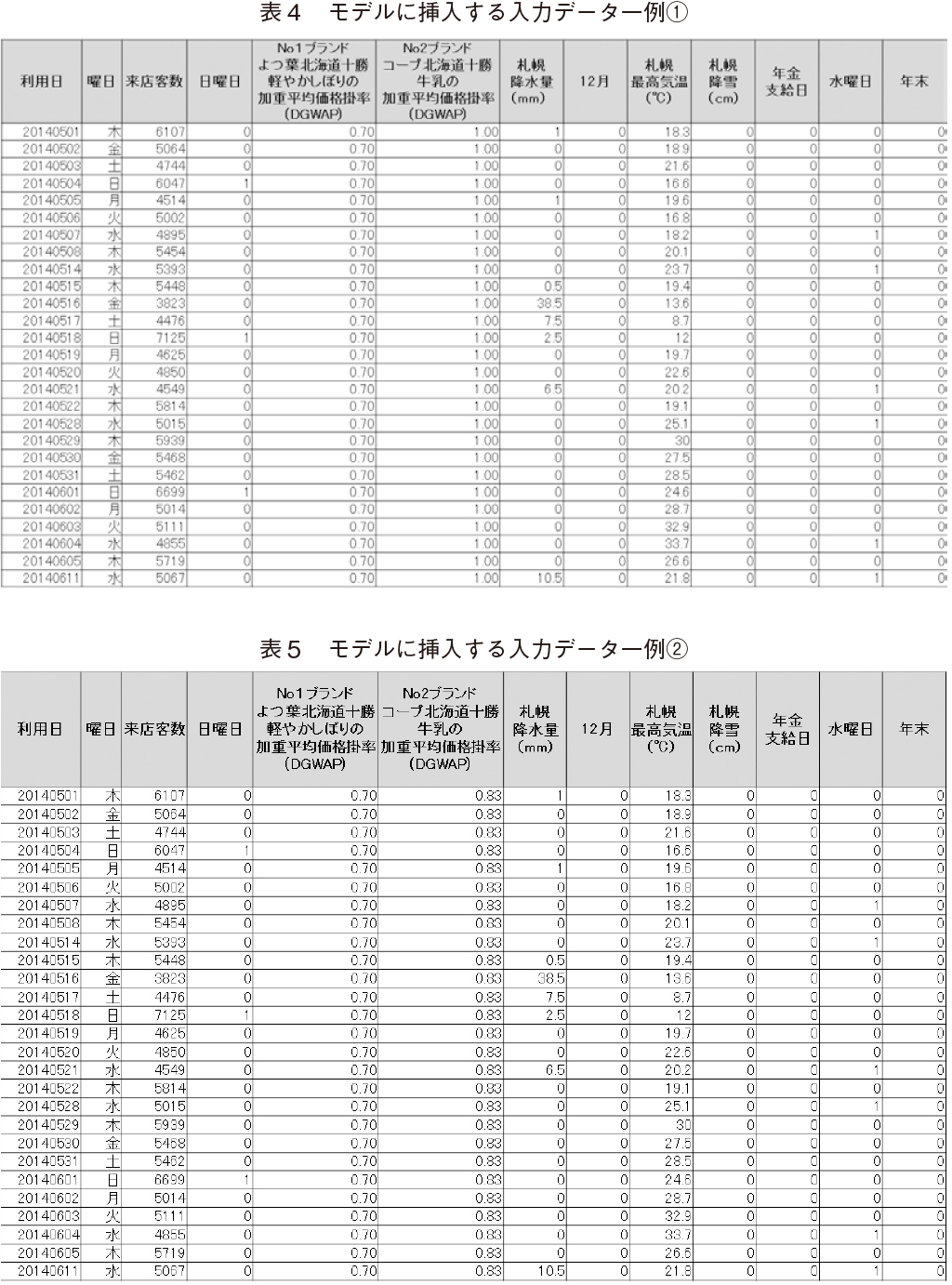
�V�~�����[�V�����̌��ʁC����ꂽNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j�ʂɂQ�N�ԓ����̗\����������W�v�����B�Q�l�Ƃ��āC�\�U�����������C�����No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�����Ԓ��ő�l��1.00�ɌŒ肵���ꍇ�́C���}�͈́i0.79�`1.00�j�̃V�~�����[�V�������ʂł���B
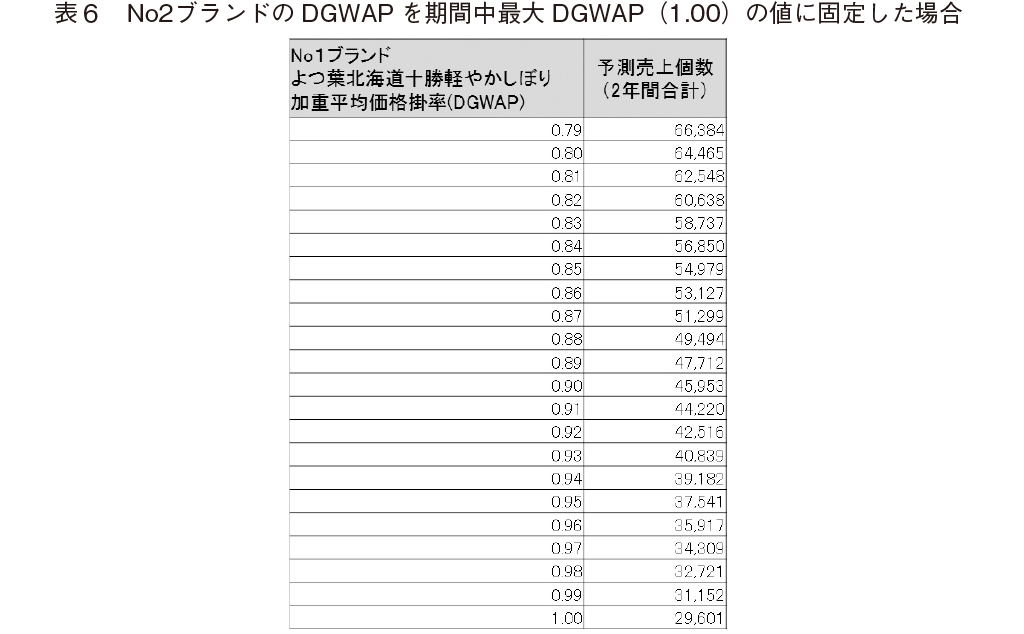
�i�T�j�Ώۃu�����h�ɂ����đS�̂ł̍ō����v�z�ݏo���i�Œ�j���i�|�C���g�̐���
�V�~�����[�V�����ɂ���ē���ꂽ�\������������ƂɁC���㑍���v�z���Z�o����B���㑍���v�z�́C���i�P������̉��i���甄�㌴���i�b��l�j���������C����ɗ\����������|���ċ��߂�B�{�߂ł́CNo1�u�����h��t�k�C���\���y�₩���ڂ�ɂ��āC�Q�N�Ԃ̔��㑍���v���ł������Œ艿�i�|�C���g�͂�����Ȃ̂�����������B
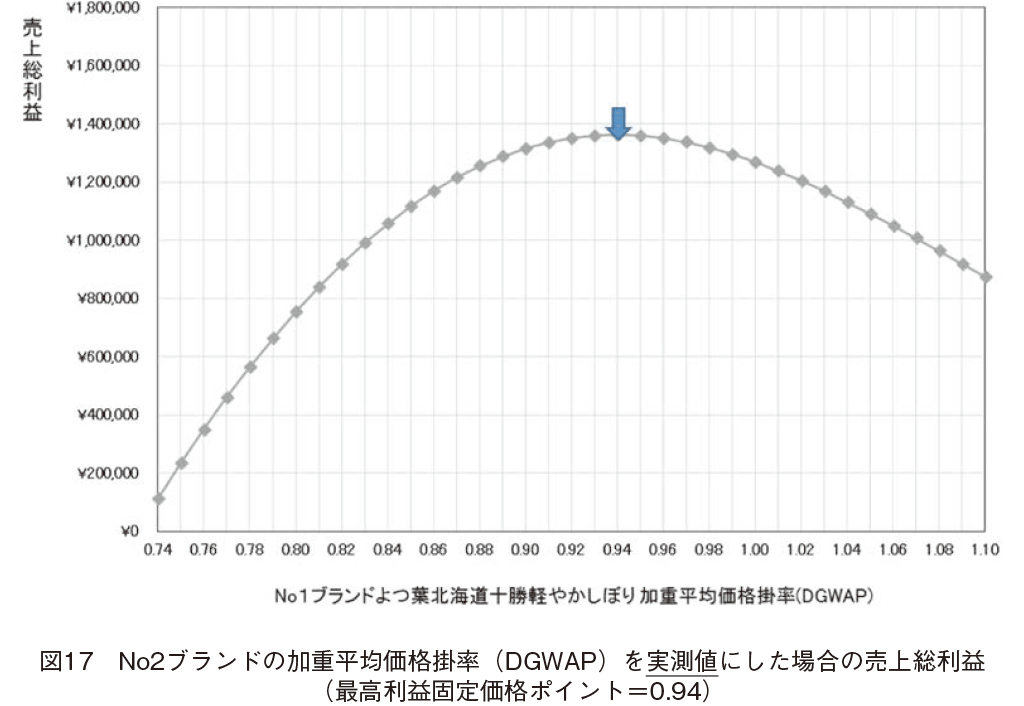
No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�Ɏ����l����}�����ꍇ�́CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j���Ƃ̔��㑍���v���O���t�������̂��C�}17�ł���B�}17�Ŏ��������ʂɂ��ƁCNo1�u�����h��t�k�C���\���y�₩���ڂ肪�ł����v�ݏo���Œ艿�i�|�C���g�́C0.94�ł������B
�y23�Łz
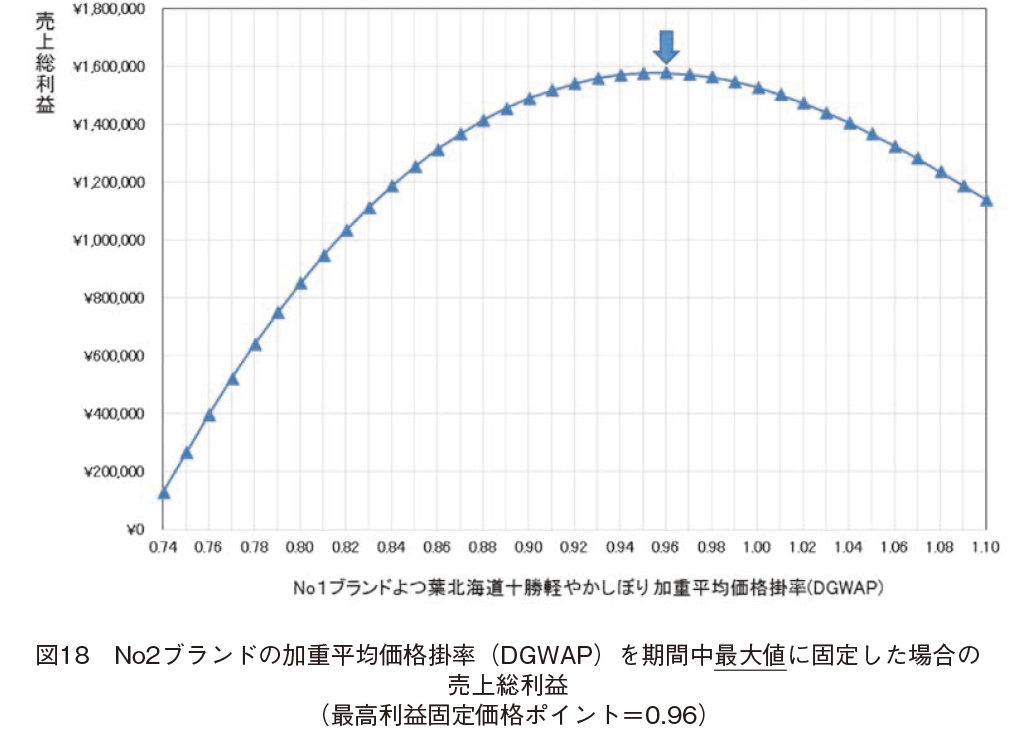
No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�����Ԓ��ő�l��1.00�ɌŒ肵���ꍇ�CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j���Ƃ̔��㑍���v���O���t�������̂��C�}18�ł���B�}18�Ŏ��������ʂɂ��ƁC�Ώۃu�����h�ł����t�k�C���\���y�₩���ڂ肪�ł����v�ݏo���Œ艿�i�|�C���g�́C0.96�ł������B
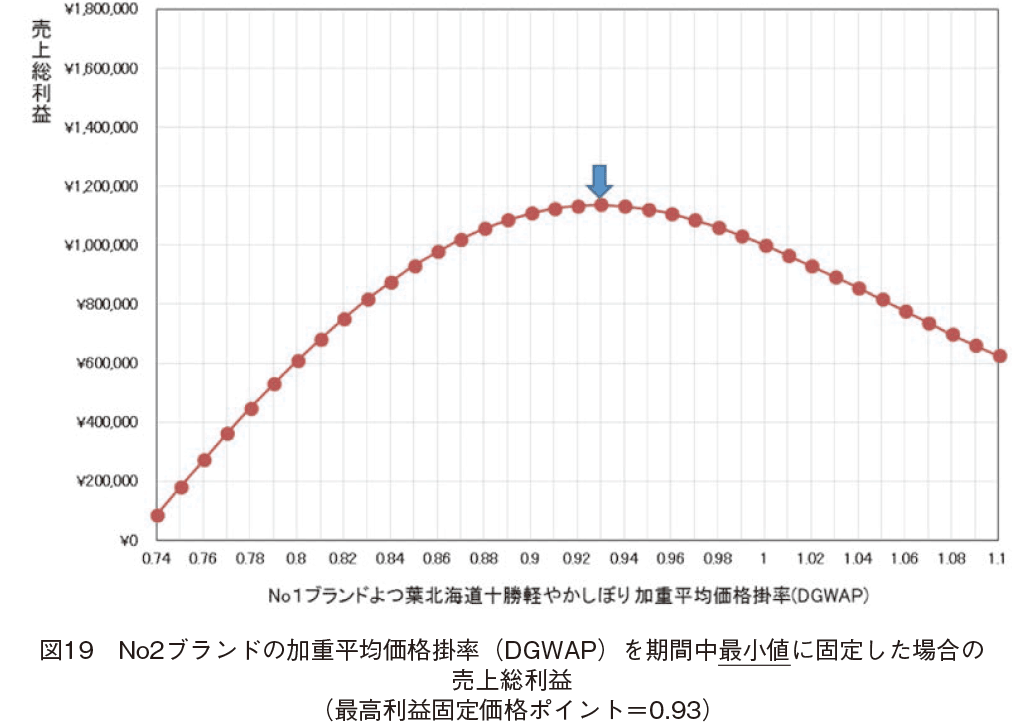
No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�����Ԓ��ŏ��l��0.83�ɌŒ肵���ꍇ�́CNo1�u�����h��t�k�C���\���y�₩���ڂ�̉��d���ω��i�|���iDGWAP�j���Ƃ̔��㑍���v���O���t�������̂��C�}19�ł���B�}19�Ŏ��������ʂɂ��ƁC�Ώۃu�����h�ł����t�k�C���\���y�₩���ڂ肪�ł����v�ݏo���Œ艿�i�|�C���g�́C0.93�ł������B
�y25�Łz
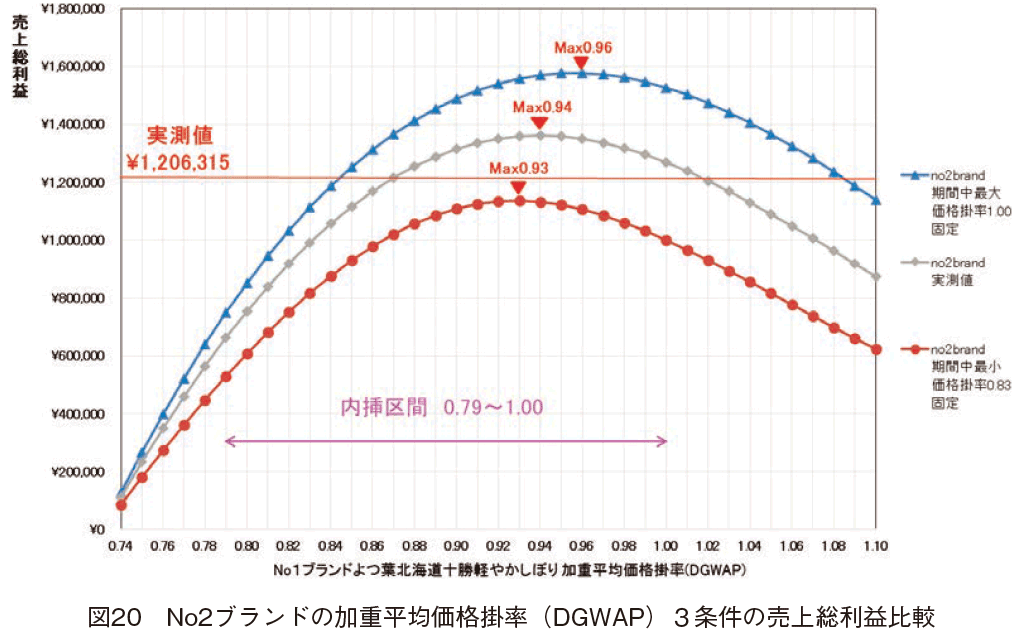
�O�q�������㑍���v�̎Z�o���@�ŁC���㌴�������[�J�[��]�������i��60���Ɖ��肵�ĂQ�N�ԍ��v�̔��㑍���v�̎����l�����߂�ƁC1,206,315�~�ł������B�����ł���No2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�R�������ꂼ��̍ō����i�|�C���g���C���̎����l�̔��㑍���v�Ɣ�r����ƁC�����l�Ɗ��Ԓ��ő�l�ɌŒ肵���ꍇ�̂Q�p�^�[���͏���C���Ԓ��ŏ��l�ɌŒ肵���ꍇ�̂݉���錋�ʂƂȂ����i�}20�j�B
No1�u�����h��t�k�C���\���y�₩���ڂ�́C���d���ω��i�|���iDGWAP�j��0.94�Ŕ̔����Ă���������Q�N�Ԃň�ԑ����C�}11�Ō����ꍇ�C�ቿ�i���x�̈�̉E�[�Ɉʒu���Ă��邱�Ƃ������Ă���BNo2�u�����h�R�[�v�k�C���\�������̉��d���ω��i�|���iDGWAP�j�̏����������l�̏ꍇ�C�Ώۊ��ԂQ�N�Ԃɂ����čō����v�z�ݏo���Œ艿�i�|�C���g�͌��ʓI��0.94�ł������B����0.94�łQ�N�ԌŒ肵�Ă���C���ۂ̔��㑍���v�z��1,362,252�~�ƂȂ�C���ۂ����邱�ƂɂȂ����͂��ł���C�편�������v�����݂��Ă������Ƃ���������B�ȏ�̂��Ƃ܂���ƁC�����ۑ�ł��闘�v�z�ő剻�ݏo�����i�|�C���g�̐���͉\�ł��邱�Ƃ����炩�ƂȂ����B
�y26�Łz
�V�|�P�D���_
�ȏ�̕��͎��Ⴉ��C�����J�e�S���[�S�̂ł̏ꍇ�ɂ��C�ʃu�����h�̏ꍇ�ɂ��C�ȉ��R�̌��������̓J�e�S���[�S�̂ł͎��F���x���̌����ŁC�ʃu�����h���x���ł͎��F���x���ɉ����āC���l�I�Ȍ��������Ď��{�ł����B
H1�D ���i�̎��v�Ȑ��̓O�[�e���x���O�Ȑ��̌X���������B
H2�D ����҂̌ʃu�����h�ɑ��鉿�i���x���Ⴂ�قǁC�ቿ�i���x�̈�̕��͂��L���Ȃ�B
H3�D ����҂̌ʃu�����h�ɑ��鉿�i���x�������قǁC�ቿ�i���x�̈�O�̕��������C�X������ɂȂ�B
�܂��ʃu�����h�ł̌����ۑ�ł���C�u���v�z�ő剻�ݏo�����i�|�C���g�̐���v���T���v�������m�ۂł����ꍇ�ɁC����ł��邱�Ƃ����炩�ƂȂ����B
�V�|�Q�D�C���v���P�[�V����
�{�����̃C���v���P�[�V�����Ƃ��āC�傫���R�̓_�������Ă����B
���ɁC�O�[�e���x���O�Ȑ��̑��݂����炩�ƂȂ�C���v�ő剻���i����g�g�݂�^�����B
���ɁC����҂̉��i���x�̈Ⴂ�ɂ���āC�O�[�e���x���O�Ȑ��̌`��́C�ቿ�i���x�̈�̕��C�Ȑ��̌X�����قȂ邱�Ƃ������C�^�[�Q�b�g�ɂ�鉿�i����g�g�݂̒��ł����B
�y27�Łz��O�ɁC�ʃu�����h�����C���ƂȂ邪�C���v�ő剻�̃V�~�����[�V�������@����C���̉��i�|�C���g����̕��@���������B
����̉ۑ�Ƃ��ẮC�O�[�e���x���O�Ȑ��̑��݂́C�����J�e�S���[�Ɍ����Ċm�F�ł������̂́C���̏��i�J�e�S���[�ɂ����Ă����̏o���̗L�����������C��ʉ���}��K�v������B���l�ɁC�ʃu�����h�̗��v�ő剻�̃V�~�����[�V�������@����葽���̕��͎���Ō������C���̎�@�����肷�邱�Ƃ������K�v������B
�܂��C�O�[�e���x���O�E���f���̐���ɂ����āC�ŏ�����덷��ł́C����l��q���ɏE�����߁C��Ό덷�̘a�̍ŏ�����Ő�������{���邱�Ƃ��]�܂����B�������C����̂��߂̌덷��̌��������コ��ɍs���K�v������B�O�[�e���x���O�E���f���ƒ�����A�Ƃ̓��Ă͂܂�̗ǂ��Ɋւ���덷�̑傫�������������Ƃ���C�ŏ�����덷��i���`����F2633916���O�[�e���x���O�E���f������F2686523�j�ł���Ό덷�̘a�̍ŏ�����i���`����F23505���O�[�e���x���O�E���f������F25112�j�ł�������A���������B����͍���̉ۑ�ƂȂ�C����Ɋւ��Ă����̕��͎����ςݏd�˂Ă����K�v������B�Ȃ��]�����f����������ł������O�[�e���x���O�E���f���̃��f�����ɂ��ẮA�ϔN�̌��Ď����ł���A���̌��������{�������C����ɂ��Ă͎��ʂ����߂ďq�ׂ����B
�y�ӎ��z�{�����́C�i�~���N�̕���28�N�x�u���̊w�p�A���v�w�p�������̎Љ���w�p�����ɂ�錤���������Ă���B�����ė��p����ID-POS �f�[�^�̓R�[�v�����ۂ�̂����ӂŗ��p�����Ē������B���҂ɑ��āC�����ɋL���Č������Ӑ\���グ�鎟��ł���B
�ED. Kahneman and A. Tversky�i1979�j,�hProspect Theory :An Analysis of Decision Under Risk,�h Econometrica, vol.47, No.2, March.
�EH. Simon�i1989�j, Price Management, Elsevier Science Publishers B.V.
�E��c����i1995�j�C�w���i����̃}�[�P�e�B���O�x, �L��t�D
�E�ŏ㌒���E�`���G���E��c����i1997�j�C�u�O�[�e���x���O�����Ɋ�Â����i�������v�C�w�w�K�@��w�o�Ϙ_�W�x�C��34���C��Q���Cpp.117-134.
�E��c����i1999�j�C�w�}�[�P�e�B���O���i�헪�x�C�L��t�D
�EH. Albach, K. Brockhoff, E. Eymann, P. Jungen, M. Steven, and A. Luhmer �i1999�j, Theory of the Firm: Erich Gutenberg�fs Foundations and Further Developments, Springer.
�E��c����E���R���Ìb�E���䍲�D�i2002�j, �u�ቿ�i���x�̈�������O�[�e���x���O������POS �f�[�^�ɂ�錟���Ə����ɉ����ĕω����鉿�i�̎��v�Ȑ��`�̍l�@�`�j���[�����l�b�g���[�N�̊��p�`�v�C�w�w�K�@��w�o�όo�c�����N�x�C��16���Cpp.1-24.
�E�ƈ�L�F�i2008�j�C�u���i臒l�̐���Ɖ��i�J�X�^�}�C�[�[�V�����̉\���v�C���{���v�w��C��37�y28�Łz����Q���Cpp.261-277.
�E���㗲�i2015�j�C�u���̌��p�Ɖ��i�Ɋւ����l�@�v�C�w������w��w�@���w�����_�W�x�C��43���Cpp.1-12�D