y169Εz
Local Powers of the MLE-Based Test for the Panel Fractional Ornstein-Uhlenbeck Process
Katsuto Tanaka
Faculty of Economics, Gakushuin University, Tokyo, Japan
Abstract
We consider the testing problem associated with the panel or longitudinal fractional Ornstein-Uhlenbeck (fO-U) processes driven by independent fractional Brownian motions (fBms), where the sign of the drift parameter of each fO-U process is tested, assuming that the Hurst parameter H is known. Since the test has a trivial consistent property against a fixed alternative, we employ the local alternative hypothesis that the drift parameter is close to the null in the order of 1/(TN η), where T is the sampling span and N is the cross section dimension with 0 < η < 1. Then, for a given value of H, we compute the local power as N increases with any T .
1. Introduction
The present paper deals with the panel or longitudinal fO-U process defined on the time interval [0,T]. By ‘panel’ or ‘longitudinal’ it is meant in the present context that data contain multiple observations in the cross section direction at each time for each process. For this purpose let us consider the fO-U process at the ith cross section, whose stochastic differential is given by
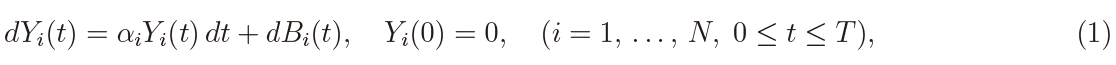
where αi (∈ R) is an unknown drift parameter and N is the cross-section dimension, whereas {Bi(t)} is the fBm of the known Hurst parameter H ∈ (0, 1). It is assumed that {Bi(t)} (i = 1, ..., N ) are independent of each other. Note that {Bi(t)} reduces to the standard Brownian motion when H = 1/2. The fO-U process {Yi(t)} is referred to as the ergodic case when αi < 0, as the non-ergodic case when αi > 0, and as the boundary case when αi = 0. Note that the stochastic differential in (1) is equivalent to
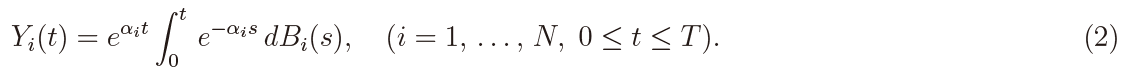
The main purpose of the present paper is to discuss the testing problem given by
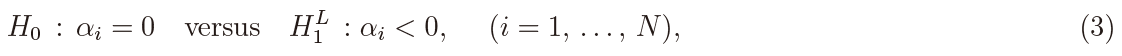
which tests against the ergodic case, or
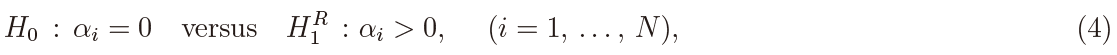
which tests against the non-ergodic case. Note that Yi(t) reduces to Bi(t) under H0. Of course some other alternatives are possible when N > 1, but we restrict our attention to the above cases because of simplicity.
y170Εz
The test statistic we consider here is based on the maximum likelihood estimator (MLE) of α = (α1 , ..., αN)′. The likelihood for α is given, from Kleptsyna and Le Breton (2002), by
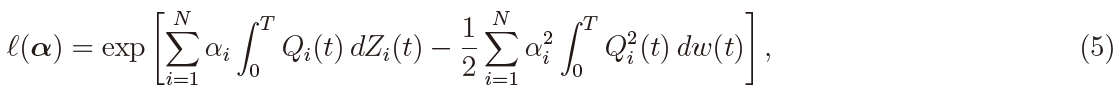
where
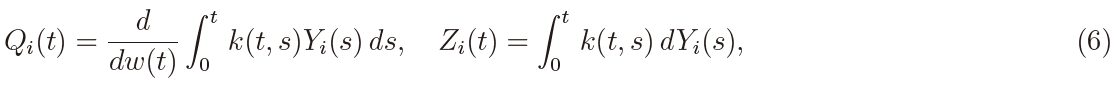
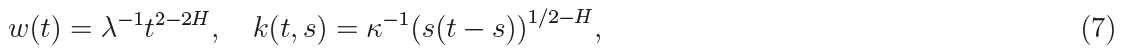
with λ = 2HΓ(3 − 2H)Γ(H + 1/2)/Γ(3/2 − H) and κ = 2HΓ(3/2 − H)Γ(H + 1/2).
The sample paths of the process Qi(t) in (6) belong to L2 ([0,T ], dw). The process Zi (t) in (6) is a Gaussian semimartingale so that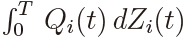 
is the Ito integral and it has the decomposition
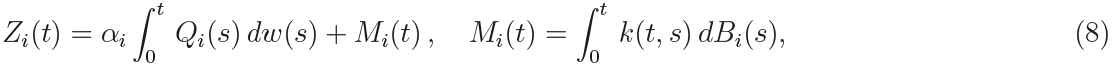
where Mi(t) is the fundamental martingale with the quadratic variation w(t) in (7) and Cov(Mi (s),Mi (t)) = λ−1( min(s, t))2−2H, which was discussed in Norros et al. (1999) in connection with approximating Bi(t) by Mi(t).
When N = 1, this testing problem was earlier discussed in Moers (2012), Tanaka (2013, 2015), and Kukush et al. (2017). One important necessity for the present test is that the methods of constructing the estimators and their asymptotic properties essentially depend on the sign of the drift parameter (Kukush et al. (2017)). In connection with econometric problems, the present test is referred to as the unit root test. This is because of the relationship between the fO-U process and the discrete-time near-unit root process defined by
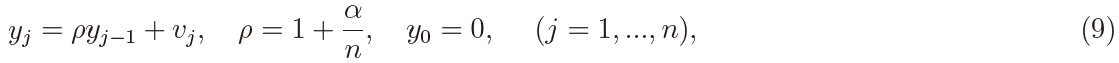
where the error process { vj } is a stationary long-memory process generated by
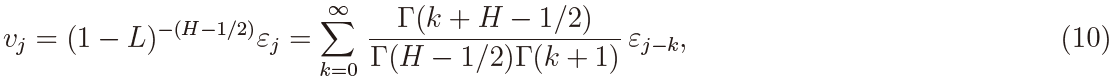
with 1/2 < H < 1, L being the lag-operator, and { εj } ∼ i.i.d.(0, σ2). Then it holds (Davydov (1970)) that
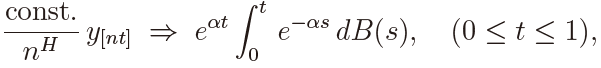
where 
signifies weak convergence as n → ∞. The discrete-time process { yj } in (9) is said to have a unit root when α = 0. Thus the testing problem for α = 0 is called the unit root test. Note that the parameter α in (9) plays the same role as the drift parameter αi in the fO-U process in (1) or (2).
y171Εz
Returning to the panel fO-U process in (1), suppose first that N = 1 and let us proceed without the subsript i for each quantity. Then the MLE of α is given for any H ∈ (0, 1) by
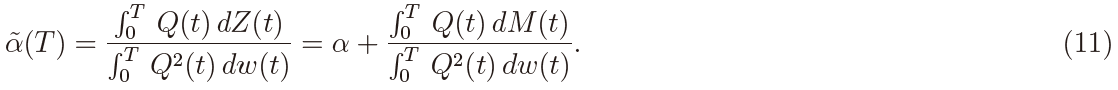
In particular, when α = 0, we have Y (t) = B(t) and the self-similarity property of B(t) yields
which shows that the distribution of T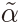 
(T ) does not depend on T when α = 0.
Although 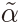(T ) is defined in the same way for any α, unlike the least squares estimator (LSE), its asymptotic distribution as T → ∞ is different among the signs of α because it holds that
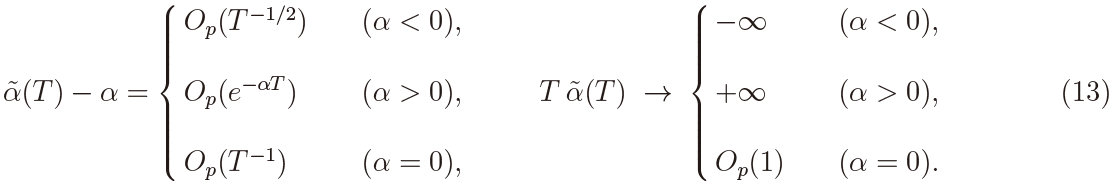
More specifically, it holds that, for α < 0,
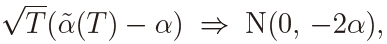
which was proved in Kleptsyna and Le Breton (2002), whereas, for α > 0,
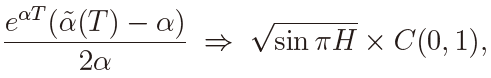
where C(0, 1) is a standard Cauchy random variable, which was proved in Tanaka (2015). Then we have
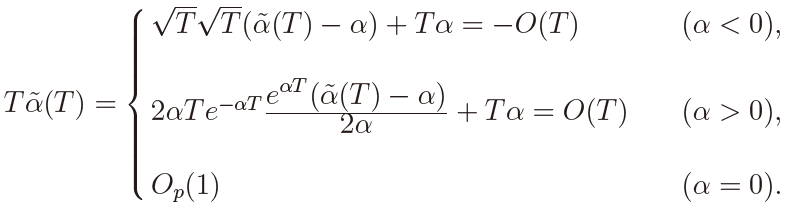
It follows that the test based on 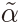( T ) is consistent and has trivial limting powers as T → ∞ against α < 0 and α > 0. Moreover we have the following theorem.
Theorem 1. For the fO-U process in (1) with N = 1, let us consider the testing problems (3) and (4). Then the powers of the tests based on 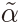(T) in (11) do not depend on each value of α and T , but on α × T .
It follows from Theorem 1 that the present test is consistent and has trivial limiting powers as Because of this fact there is no point in examining y172Εz limiting powers as T → ∞ or |α| → ∞. Instead we pursue limiting local powers under a sequence of local alternatives which depend on the sampling interval T and the cross section dimension N .
In Section 2, dealing with the panel fO-U process in (1), we consider the local alter-native H1 : αi = δN /T , where δN = δ/Nη with δ being a fixed constant and η ∈(0, 1). We present a feasible way of computing finite sample local powers as well as limiting local powers of the MLE-based test as N → ∞. Section 3 demonstrates that the MLE-based test is asymptotically efficient. Section 4 presents graphically the local powers at the 5% level for any value of T and various values of N including N = ∞. Section 5 concludes this paper, where the difficulty of the LSE-based test is mentioned together with an extension of the present test. The proofs of theorems are given in the Appendix.
2. Powers under the local alternative
In this section we deal with the testing problems in (3) and (4), where we consider the local alternatives given by
where δ is a constant with δ < 0 being the ergodic alternative and δ > 0 being the non-ergodic alternative, whereas η ∈ (0, 1) is determined later so that the limiting power becomes nontrivial as N → ∞.
We consider a test based on the MLE of α = (α1, ..., αN)′. For this purpose the MLE of α is computed under the assumption that αi = α for i = 1, ..., N . Then the MLE of α is given from (5) as
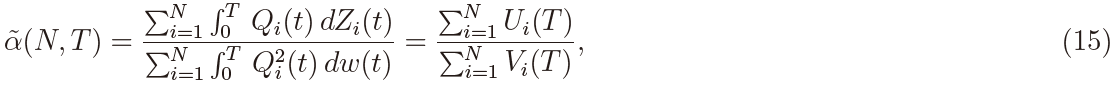
where
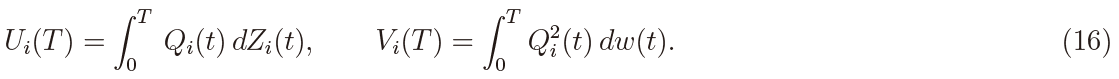
To compute the distribution of 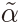(N, T ) the following property is useful.
Theorem 2. It holds that, under H0 : α = 0 and H1 : αi = α = δN /T ,
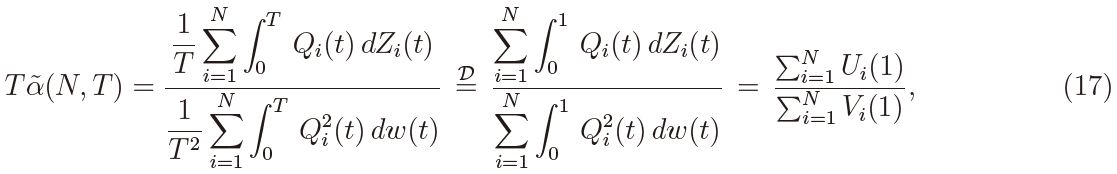
where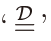 
stands for the distributional equivalence.
We now use T 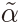(N, T ) as a test statistic. For the ergodic alternative with α < 0, the null hypothesis of α = 0 is rejected when T 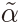(N, T ) is small and the power of the test at the 100 γ% is computed as P (T 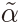(N, T ) < zγ), where zγ is the 100γ% point of the
y173Εz
null distribution of T 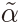(N, T ). The following theorem describes how to compute the local power against the ergodic alternative when N is finite.
Theorem 3. The power of the present test at the 100γ% level against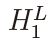 
: α = δN /T with δN < 0 is computed as
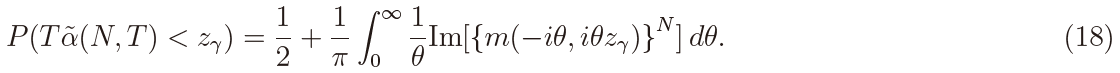
Here zγ is the 100γ% point of the null distribution of T 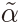(N, T ) and m(θ1, θ2) is the joint moment generating function (m.g.f.) of Ui(1) and Vi(1) given by
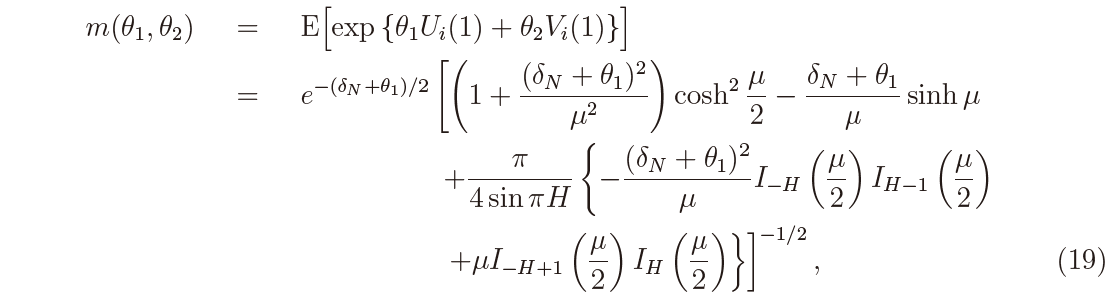
where µ =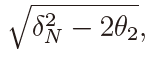 
whereas Iν(z) is the modified Bessel function of the first kind defined by
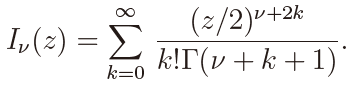
The local power against the non-ergodic alternative at the 100γ% level is computed as P (T 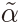(N, T ) >z1−γ). The m.g.f. in (19) was first obtained in Kleptsyna and Le Breton (2002) (see also Tanaka (2015)). It is noticed in (19) that the m.g.f. remains the same when H is replaced by 1 − H. This means that the MLE under H is the same as that under 1 − H. Thus the MLE can be applied to 0 < H < 1, and the distribution of the MLE is symmetric around H = 1/2.
The powers of the test at the 5% level will be presented in Section 4 for various values of N including N = ∞, paying attention to the effect of the Hurst index H.
We next discuss how to compute the limiting power of the test as N → ∞. For this purpose we have
Theorem 4. Consider T 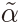(N, T ) = 
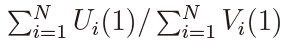under α = δN/T . When δN → 0 as N →∞ with any T , it holds that
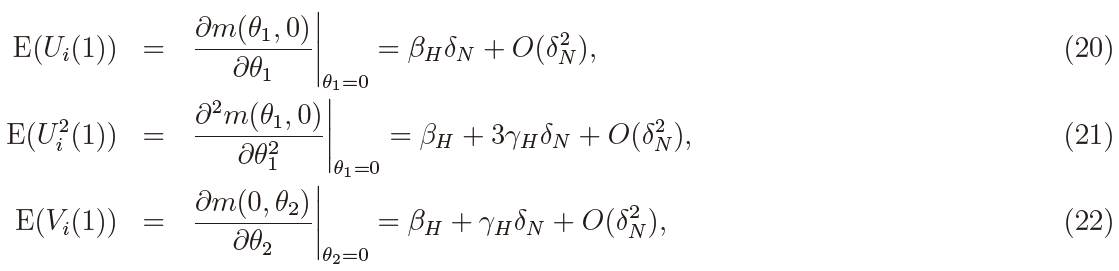
y174Εz
where
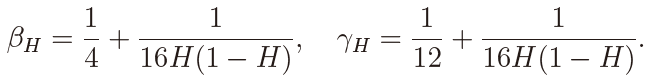
We note that the above results for H = 1/2 were earlier obtained for discrete-time panel unit root models in econometrics (Tanaka (2017)). Let us consider the situation where N → ∞. It follows from Theorem 4, the law of large numbers (LLN) and the central limit theorem (CLT) that, as N → ∞,
which leads us to establish
Theorem 5. Suppose that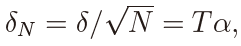 
where δ is a constant. Then it holds that, as N →∞ with any T , it holds that
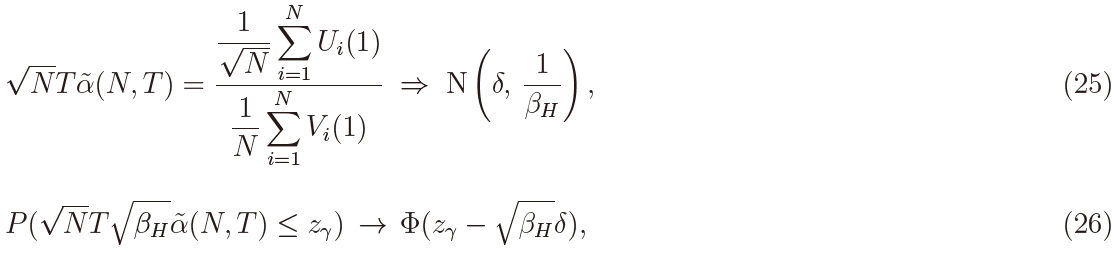
where Φ(·) is the distribution function of N(0,1).
It follows from Theorem 5 that the local alternative which yields a nontrivial result is of the form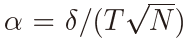 
and the limiting local power as N → ∞ can be computed from (26). Note that the asymptotic normality holds under the local alternative with any negative or positive δ. This contrasts with the case of the fixed alternative with a positive constant α, for which the statistic tends to Cauchy distribution.
The next section demonstrates that the MLE-based test discussed in this section is asymptotically efficient.
3. Asymptotic efficiency of the MLE-based test
Suppose that the panel fractional O-U model is given by
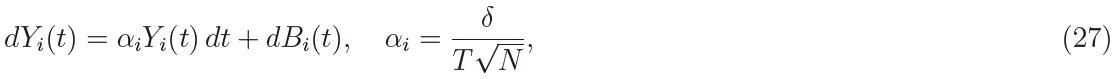
and consider the testing problem
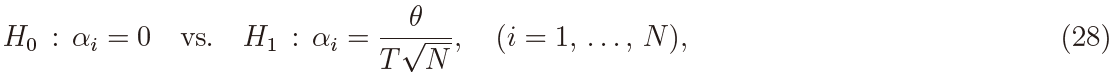
y175Εz
where θ is a given constant. This is a test against a simple alternative.
Then the Neyman-Pearson lemma tells us that the test rejects H0 when
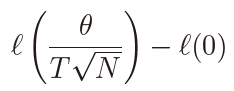
takes large values is the most powerful (MP), where ℓ(α) is the likelihood for α given by
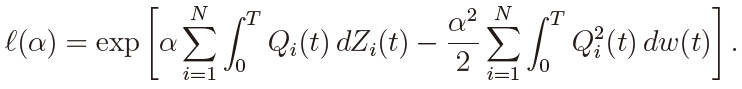
Thus the MP test rejects H0 when
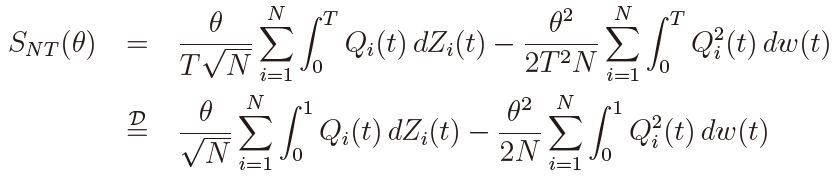
takes large values. It follows from (23) and (24) that the MP statistic SNT (θ) converges to
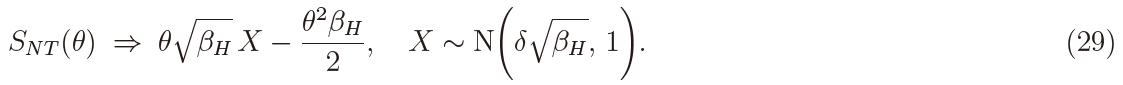
Thus it holds that
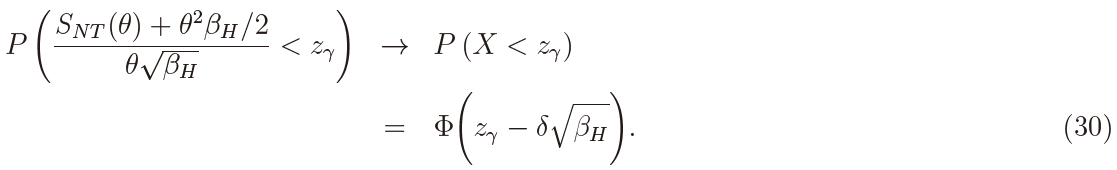
It is seen that the power function does not depend on θ, which implies that the MP test based on SNT (θ) is UMP, and the MLE-based test is asymptotically efficient because the two power functions coincide.
4. Computation of local powers
Here we report powers of our tests against the ergodic and non-ergodic alternatives at the 5% significance level. For this purpose we first compute the 5% and 95% points of the null distribution of the statistic T (N, T ) for various values of N and H. These can be obtained from (18) by putting δN = 0. Table 1 reports these percent points for N = 1, 10, 50 and H = 0.5, 0.7, 0.9. It is recognized that, for each N , the statistic becomes slightly more concentrated as H gets away from H = 0.5. Note that the distirbutions remain unchanged with H replaced by 1 − H.
y176Εz
Table 1. 5% and 95% points of the distribution of T 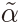(N,T ) under α = 0
Figure 1 draws the null densities of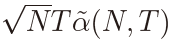 
for N = 1 with H = 0.5 ,0.7 ,0.9 and Figure 2 for N = 50 with the same values of H. Note that we have added 
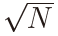to the factor so that the distribution does not depend on N asymptotically. In fact it follows from Theorem 5 that 
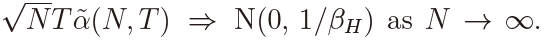It is seen from these figures that
iaj When N = 1, the distribution is far from normal. The distribution for N = 1 with H = 0.5 is called the unit root distribution in econometrics. As N becomes large, however, it tends to normal with the mean 0 because of the CLT.
ibj For fixed N , the distribution becomes slightly more concentrated as H gets away from H = 0.5, as was also recognized in Table 1.
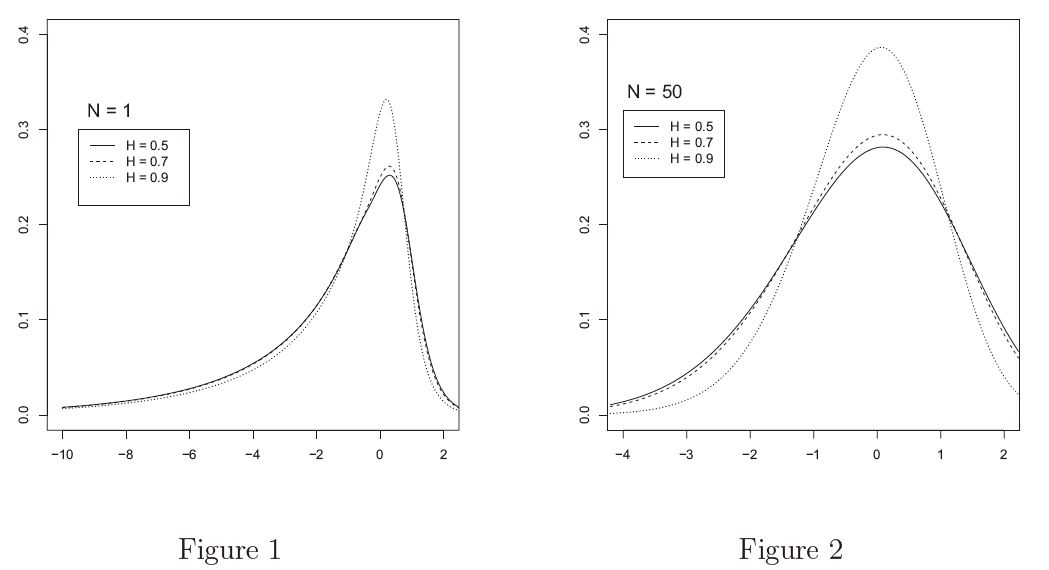
Figure 3 shows the densities of 
under the local ergodic alternative α =δ / (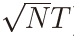
) with δ = −1 and N = 1, whereas Figure 4 shows those densities with δ = −1 and N = 50. When N = 1, these densities are still skewed to the left, but not so much as the null densities shown in Figure 1. When N = 50, these are quite close to the
y177Εz
density of N( −1, 1/βH), where δ = −1 and βH = 1/4 + 1/(16H(1 − H)). It follows that the distribution becomes more concentrated as H gets away from H = 0.5. Figure 5 draws the corresponding densities under the local non-ergodic alternative with δ = 1 and N = 50. These densities are close to those of N(1, 1/βH).
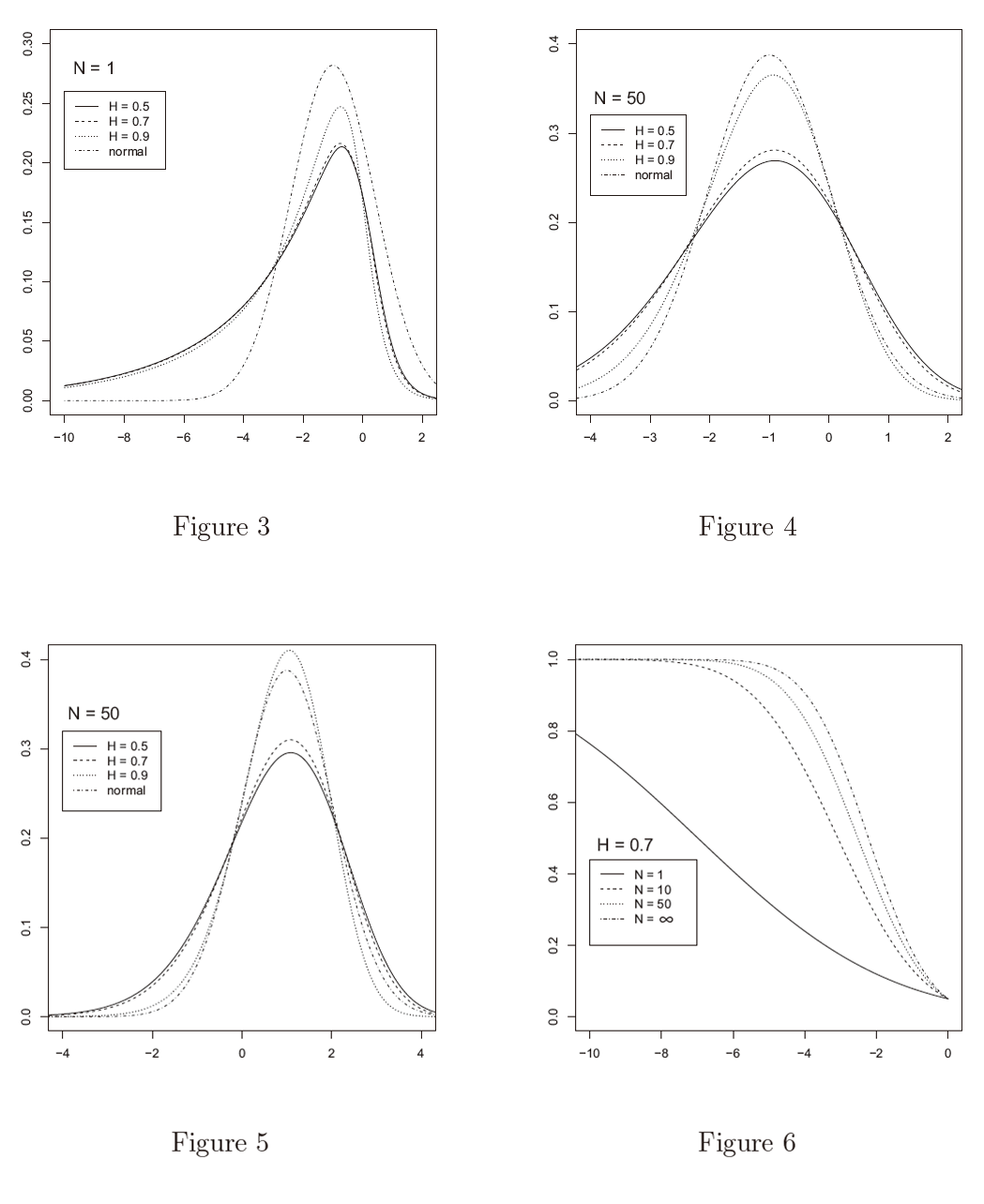
Figure 6 presents the local powers of the test against the ergodic alternative with H = 0.7. The powers for N < ∞ were computed from (26). The limiting power for N = ∞ is also shown, which was computed from (18). It is seen that the finite sample
y178Εz
powers increase with N and converge to the limiting power from below. This is not trivial because the local alternative with 
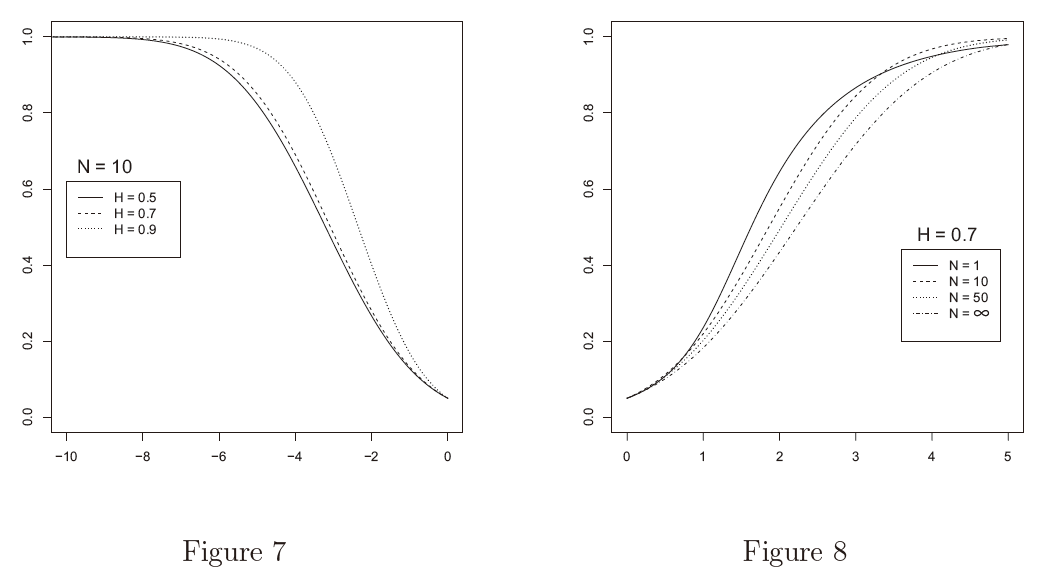
is in the neighborhood of the null in the order of 
which converges to the null. The fact that the covergence of finite sample powers to the limiting power from below is specific to the ergodic alternative. It will be seen in Figure 8 that the finite sample powers against the non-ergodic alternative converge from above to the limiting power. Figure 7 compares, among H, the finite sample performance of the test against the ergodic alternative when N = 10. It is seen that the test is more powerful when H gets away from H = 0.5.
Figure 8 shows the finite sample and limiting local powers against the non-ergodic alternative with H = 0.7. It is seen that the power performance is different between the ergodic and non-ergodic alternatives. The test is more powerful against the non-ergodic. It is also seen that the finite sample powers converge to the limiting power from above, as was mentioned before.
5. Concluding remarks
We have considered the MLE-based test for the sign of the drift parameter in the panel fO-U process with the Hurst index H known, which tests for the process to be the fBm against the ergodic or non-ergodic fO-U process. Because the test is consistent against the fixed alternative as the cross section dimension N → ∞, we have assumed a local alternative close to the null in the order of T −1N −η, where T is any time span and 0 < η < 1. It was found that η = 1/2 yields a non-trivial power as N → ∞. It was also demonstrated that the MLE-based test is asymptotically efficient in the sense that the power function of the MP test coincides with that of the MLE-based test. The power performance of the test was examined for various values of N including N = ∞ by paying attention to the effect of the value of H.
The present model may be extended to the fractional Vasicek model
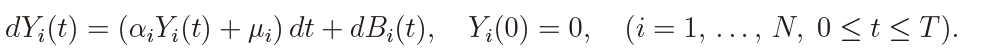
y179Εz
For the time series case with N = 1, the MLEs of µ = µi and α = αi were discussed in Tanaka et al. (2020).
It is also interesting to compare the power of the present test with that of the LSE- based test. Tanaka (2020) compared the LSE and MLE in the case of N = 1. Suppose that H ∈(1/2, 1). Then, assuming α = αi (i = 1, ..., N ), the LSE of α in (1) is given by
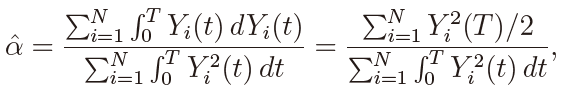
where the integral in the numerator is of Riemann-Stieltjes type. It might be argued that the power of the LSE-based test could be computed in the same way as that of the MLE-based test. This, however, is not the case because the joint m.g.f. of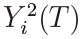 
and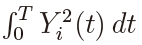 
has never been derived even under the null H0 : α = 0. In fact, the joint m.g.f. of 
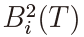and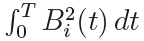 
is unknown, although an approximation was suggested in Tanaka (2014). This is a topic for future research.
In the present paper the cross-sectional independence was assumed, that is, the frac- tional Brownian motions B1(t), ..., BN (t) which generate the panel fO-U processes are independent of each other. An extension to the cross-sectional dependence is also another topic to be pursued.
Appendix
Proof of Theorem 1 : Let xγ(T ) be the 100γ% point of the null distribution of 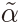(T ) under the sampling interval T . Then the power of the test against α < 0 at the significance level γ is computed, by using the formula in Imhof (1961), as
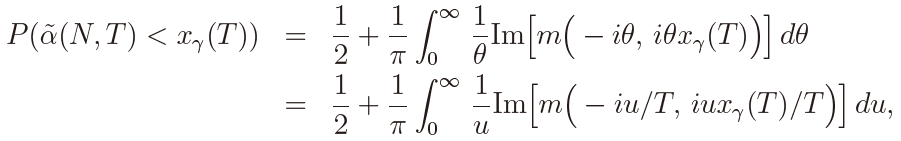
where m(θ1, θ2) is the m.g.f. of Ui(T ) and Vi(T ) in (16), which is given by Kleptsyna and Le Breton (2002) as
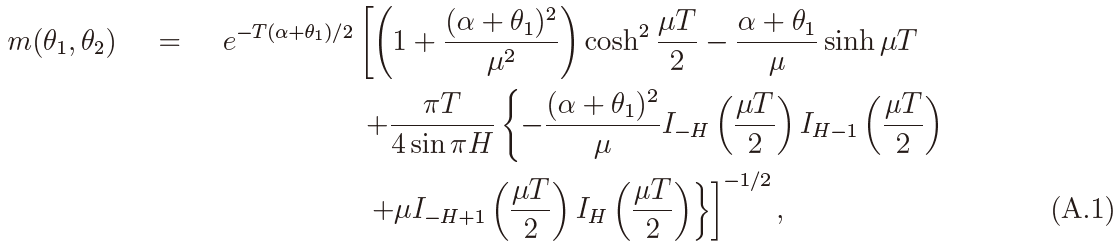
where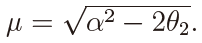 
Then it holds that
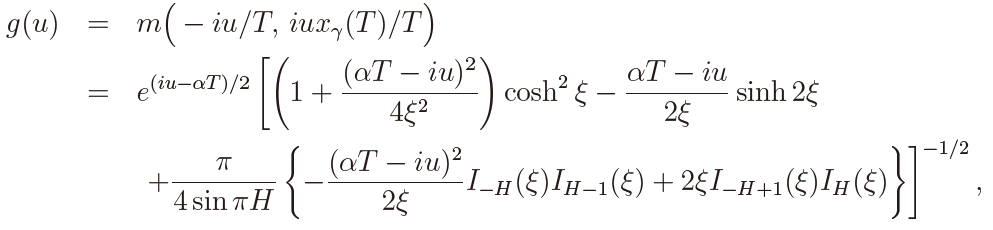
y180Εz
where
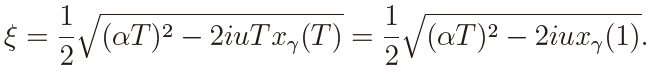
This last equality, that is, T xγ(T ) = xγ(1), comes from (12). Then it is seen from the form of g(u) that the power depends only on α×T , and does not depend on each value of α and T , which establishes Theorem 1.
Proof of Theorem 2: Let us denote the m.g.f. m(θ1, θ2) in (A.1) as m(θ1, θ2; α, T ) to express its dependence on α and T explicitly. Then it can be checked that, for α = δN /T , the joint m.g.f. of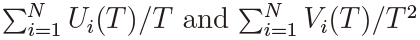 
is given by
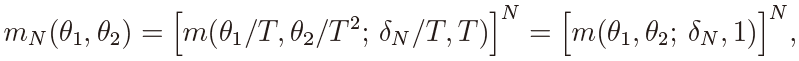
which means that the joint distribution of 
with α = δN /T is the same as that of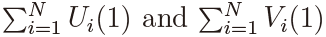 
with α = δN . This also holds for α = 0. Thus Theorem 2 is established.
Proof of Theorem 3: It follows from Theorem 2 that
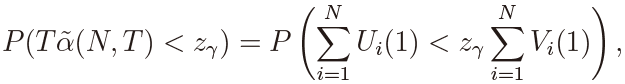
which yields (18) because of the formula in Imhof (1961). Then Theorem 3 is established from Kleptsyna and Le Breton (2002).
Proof of Theorem 4: Let m(θ1, θ2) be the joint m.g.f. of Ui(1) and Vi(1) under α = δN /T , which is given in (19). Then we have, for δN ≠ 0,
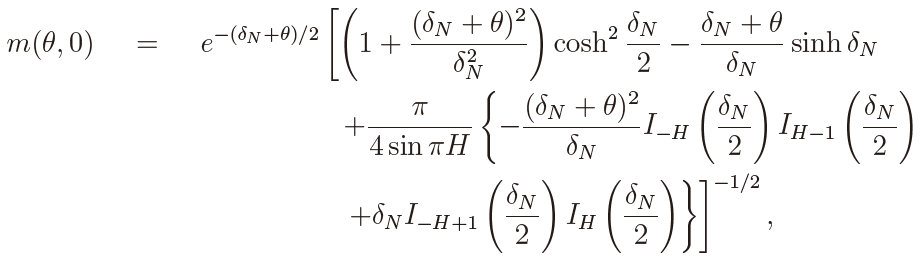
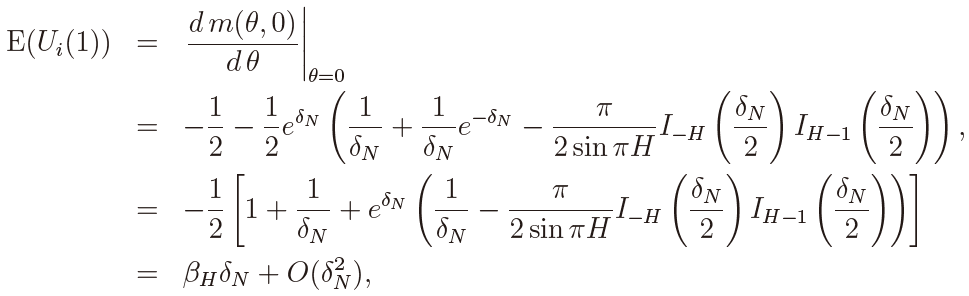
where we have used the relations
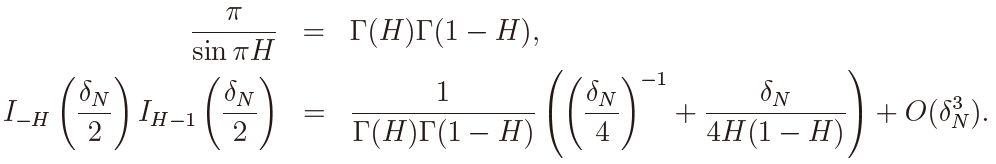
y181Εz
Simlilarly, we have
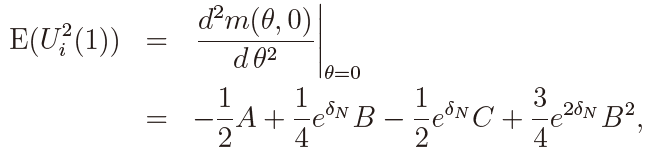
where
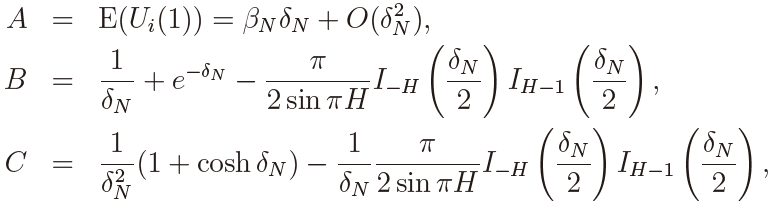
which yields the expression for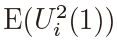 
in (21). To prove (22), we consider
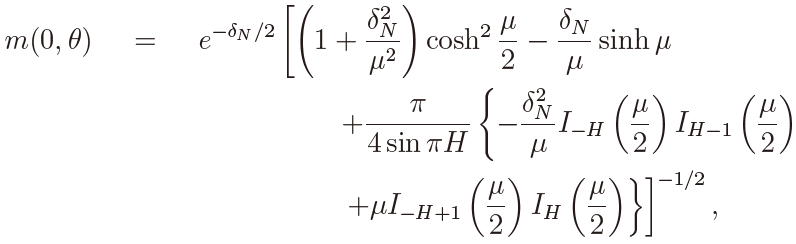
where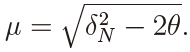 
Then we obtain, for δN > 0,
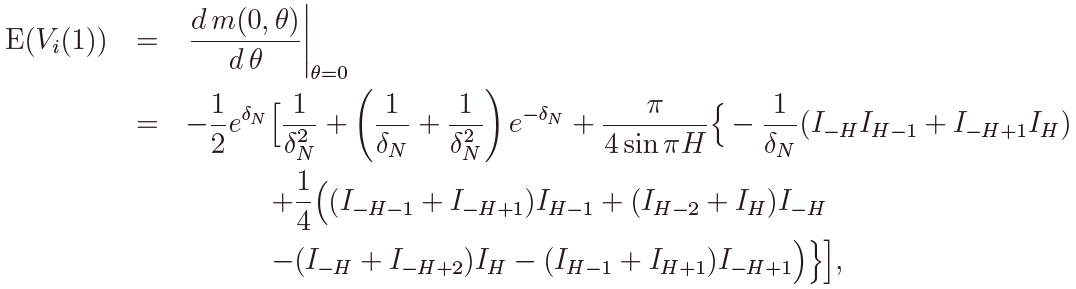
where Iν = Iν(δN /2) and we have used the relations.
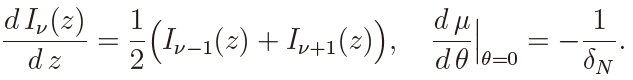
Noting further that
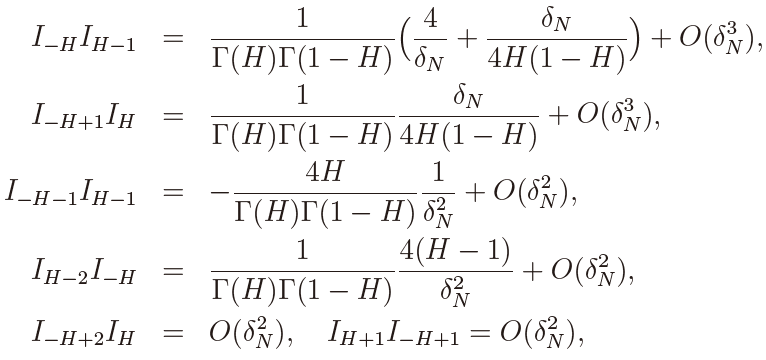
y182Εz
we can prove (22) when δN > 0. The case of δ < 0 can be proved similarly, which establishes Theorem 4.
Proofof Theorem 5: The relation in (25) can be proved because of the LLN in (23) and the CLT in (24). It follows that
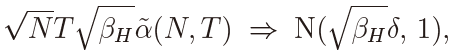
which yileds (26). Thus Theorem 5 is established.
References
Davydov, Y.A. (1970). “The invariance principle for stationary processes,” Theory of Probability and Its Applications, 15, 487-498.
Imhof, J.P. (1961). “Computing the distribution of quadratic forms in normal variables,” Biometrika, 48, 419-426.
Kleptsyna, M.L. and Le Breton, A. (2002). “Statistical analysis of the fractional Ornstein- Uhlenbeck type process,” Statistical Inference for Stochastic Processes, 5, 229-248.
Kukush, A., Mishura, Y., and Ralchenko, K. (2017). “Hypothesis testing of the drift parameter sign for fractional Ornstein-Uhlenbeck process,” Electronic Journal of Statistics, 11, 385-400.
Moers, M. (2012). “Hypothesis testing in a fractional Ornstein-Uhlenbeck model,” In- ternational Journal of Stochastic Analysis, Art. ID 268568, 23.
Norros, I., Valkeila, E., and Virtamo, J. (1999). “An elementary approach to a Girsanov formula and other analytical results on fractional Brownian motions,” Bernoulli, 5, 571-587.
Tanaka, K. (2013). “Distributions of the maximum likelihood and minimum contrast estimators associated with the fractional Ornstein-Uhlenbeck process,” Statistical Inference for Stochastic Processes, 16, 173-192.
Tanaka, K. (2014). “Distributions of quadratic functionals of the fractional Brownian motion based on a martingale approximation,” Econometric Theory, 30, 1078-1109.
Tanaka, K. (2015). “Maximum likelihood estimation for the non-ergodic fractional Ornstein-Uhlenbeck process,” Statistical Inference for Stochastic Processes, 18, 315- 332.
Tanaka, K. (2017). Time Series Analysis: Nonstationary and Noninvertible Distribution Theory, 2nd edition. Wiley, New York.
Tanaka, K. (2020). “Comparison of the LS-based estimatore and the MLE for the frac- tional Ornstein-Uhkenbeck process,” Statistical Inference for Stochastic Processes, 23, 415-434.
Tanaka, K., Xiao, W., and Yu, J. (2020).“Maximum likelihood estimation for the frac- tional Vasicek model,” Econometrics, 8, 32, 1-28.