Talent vs. Wealth in a Credentials-Based Meritocracy: A Theoretical Study
Dimitry Rtischev1j
Abstract
A meritocracy is modeled as a multiple-prize contest among agents who are heterogeneously endowed with talent and wealth and thus vary in the disutility of exerting effort and spending money to earn credentials. In equilibrium many richer but less-talented agents obtain better credentials than many poorer but more-talented ones. The paper studies the cost of the credentials race as well as the difference between the set of winning agents and the set of most-talented agents. Findings indicate that a meritocracy that relies on earned credentials may degenerate into a mediocracy that favors the wealthy and leaves the winners with little gain net of the cost of their credentials.
Keywords: meritocracy, credentialism, education, contest, socioeconomic competition
JEL classification: C72, D11, I24, Z13
In an ideal meritocracy, the best jobs are allocated to the best candidates. In practice, meritocracy usually refers to a selection process in which employers choose among job candidates based on credentials such as academic degrees and exam scores, and the candidates compete among themselves to obtain relatively better credentials.
Vested interests notwithstanding, meritocracy has attracted many strident critics among elite academics. (Young 1959, Berg 1970, Dore 1976, Dench 2006, Markovits 2019, Sandel 2020) Figuring prominently in their discourse is the concern that competition for credentials may yield not a meritocracy but a mediocracy that privileges the wealthy. Yet despite the long history of such criticism, it remains unclear to what extent the rich-but-mediocre can outcompete the poor-but-talented in a credentials race, and at what cost. This paper attempts to quantify this phenomenon using theory.
I apply the theory of multiple-prize contests developed by Siegel (2009) to compare four selection regimes: ideal meritocracy, plutocracy, credentials-based meritocracy without economic inequality, and credentials-based meritocracy with economic inequality. I compare the four selection regimes in terms of the aggregate talent of the winners as well as the effort and money spent on obtaining credentials. Building on a previous study (Rtischev 2020), I also examine how the scarcity of prizes relates to the cost of competition and the distortion away from talent toward wealth.
The first two selection regimes that I examine are baselines without competition for credentials. In y188Åzthe ideal meritocracy baseline, employers observe talent directly and assign the prize jobs to the most talented. In the plutocracy baseline, prize jobs are assigned to the wealthiest without regard for talent.
In the other two selection regimes that I examine, talent is not observable, agents invest effort and money to earn credentials which can be rank-ordered, and employers award prize jobs to the agents with the best credentials. The utility cost of effort and money to an agent are inversely related to the agentfs exogenous endowments of talent and wealth, respectively. Agents vary in terms of their talent endowments. I first analyze the case in which all agents are endowed with the same amount of wealth and then the case in which agents also vary in terms of their wealth endowments.
Equilibrium analysis reveals the areas in the talent-wealth plane where richer but less-talented agents outcompete poorer but more-talented ones. This makes it possible to quantify the difference between the set of most-talented agents and the set of agents who obtain the best credentials. The analysis also allows quantifying the cost of the credentials race and examining how it depends on the scarcity of prizes. The findings imply that instead of fostering a meritocracy, credentials competition may give rise to a mediocracy skewed toward wealth and leaving winners with little net gain.
The credentials-based selection analyzed in this paper relates to Spencefs (1973) seminal model of job-market signaling. A key implication of Spencefs work is that the signals used in hiring need not necessarily add value on the job. In other words, the effort of earning credentials signals talent but does not necessarily make the agents more productive. Although real-world credentials usually have some relevance to work performance, it is not uncommon that much of the effort to obtain the credentials is not relevant on the job. To sidestep the issue of whether credentials are valuable beyond their instrumental use in job-hunting and to establish a worst-case baseline, this paper assumes that credentials are merely signals that donft affect productivity.
The paper is organized as follows. Section 2 presents the model. Section 3 analyzes the model for a population of agents whose endowments of talent and wealth are distributed uniformly on a bounded plane. Section 4 compares credentials-based meritocracy to ideal meritocracy and plutocracy, and discusses the effects of wealth inequality. Section 5 concludes.
The model is formulated in terms of agents competing for prizes. An gagent" corresponds to a student with parental support and a gprizeh refers to a job desired by many but available to only a few. There are n agents and m < n identical prizes that each agent desires. Each agent can obtain at most one prize.
Agents are heterogeneously endowed with talent and wealth. gTalenth refers to the complex of learning aptitude, attentiveness, memory, creativity, intuition, curiosity, alertness, concentration, diligence and other personal qualities that facilitate learning and lie closer to the nature extreme of the nature-nurture continuum. gWealthh refers to the complex of parental income, savings, education, time, ability, social standing, self-esteem, house, neighborhood and other economic and social assets that facilitate learning by their children. Specifically, each agent i is exogenously endowed with talent ai and wealth wi which are positive independent random variables drawn from given distributions of talent and y189Åzwealth, respectively.
In a credentials-based meritocracy, agents compete for prizes by expending effort and money to earn credentials that qualify them for prizes. The gcredentialh of agent i is the score si ≥ 0 it obtains on a standardized exam taken by all agents. After the exam, the m highest scorers receive one prize each. gEfforth refers to the time, exertion, boredom, foregone relaxation and leisure, and other non-monetary sacrifices that a student makes which help improve exam performance. gMoneyh refers to money, time, foregone relaxation and leisure, and other sacrifices that parents make which help improve their childrenfs exam performance.
Agents gproduceh credentials per a Cobb-Douglas production function with effort e and money p as input factors:
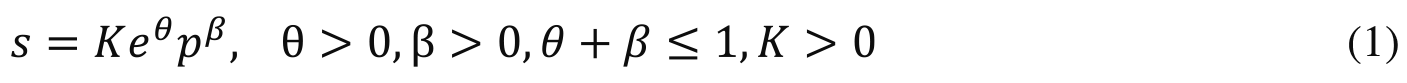
This formulation assumes decreasing returns to effort and money. It includes the case of ideal meritocracy (À=0) in which only effort matters, the case of plutocracy (Æ=0) in which only money matters, and the intermediate cases in which both effort and money matter.
In this formulation, any agent can obtain any credential by investing an appropriate combination of effort and money. Low endowments are not insurmountable barriers because rather than being stock variables used up in pursuit of credentials, the endowments a and w are parameters that indicate the rate of exchange between utility and credentials. (See Appendix for details.) Thus, a more-talented agent can obtain a given credential with less effort, but a less-talented agent can match any credential obtained by the more-talented one by making a greater effort. Analogously, wealthier parents can help their child obtain a given credential with less scrimping on other uses of their time and money, but poorer parents can match any credential obtained by the wealthier ones by scrimping more.
Let c (s, a, w) be the minimum utility cost that an agent with talent a and wealth w must incur in order to obtain credential s. The Appendix derives the optimal mix of effort and money and shows that the minimum utility cost is given by

Let the utility value of a prize to an agent be 1. If an agent i obtains score s and gains a prize, it receives utility payoff
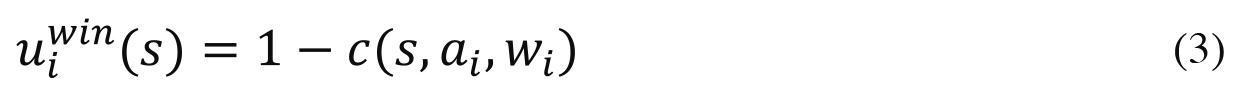
and if it fails to obtain a prize it receives utility payoff
y190Åz
The talent and wealth endowments of all agents is common knowledge. By deciding how much effort and money to invest in preparing for the exam, each agent in effect chooses its exam score. Following Siegel (2009), let us define the reach of agent i as the score ri that results in the agent getting zero utility upon winning a prize: 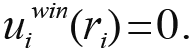 Using (2) and (3) gives the following expression for the reach of agent i :
Using (2) and (3) gives the following expression for the reach of agent i :

As proved by Siegel (2009), the only agents to obtain positive utility in equilibrium are the m agents with the highest reach. Assuming that no two agents have the same reach, let us index the agents in the order of decreasing reach, that is ri+1 < ri. Again following Siegel (2009), let us define the threshold t as the reach of the marginal agent i = m + 1 and write it as a function of the number of prizes:

As Siegel (2009) has shown, the threshold (6) is the minimum exam score that every winning agent i = 1,c, m obtains in equilibrium. The following analysis will rely on (6) to characterize the frontier in talent-wealth space along which the talented poor face off against the mediocre rich and to obtain measures of the costs and distortions engendered by the contest for credentials.
3. Analysis assuming uniformly-distributed endowments
Although the numbers of agents and prizes are integers, it is analytically convenient treat n and m as continuous variables. Let a mass of n agents varying in talent a ¸(0, A) and wealth w ¸(0,W) be uniformly distributed according to the density function 2j
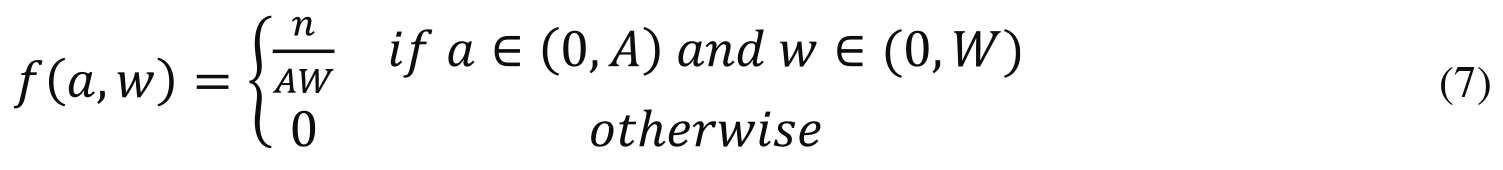
3.1@Baselines: ideal meritocracy and plutocracy
In the ideal meritocracy baseline, agentsf talent is directly observable. Since by assumption credentials do not affect on-the-job performance, the most efficient way to allocate prize jobs is to award them to the m most-talented agents regardless of the credentials they may have earned, if any. Employers ignore credentials and the agents do not invest any time or money in getting them. The total talent among the winners is
y191Åz
where 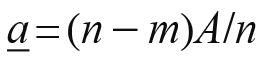 is the talent of the least-talented winner. (See Figure 1a) Evaluating (8) yields
is the talent of the least-talented winner. (See Figure 1a) Evaluating (8) yields

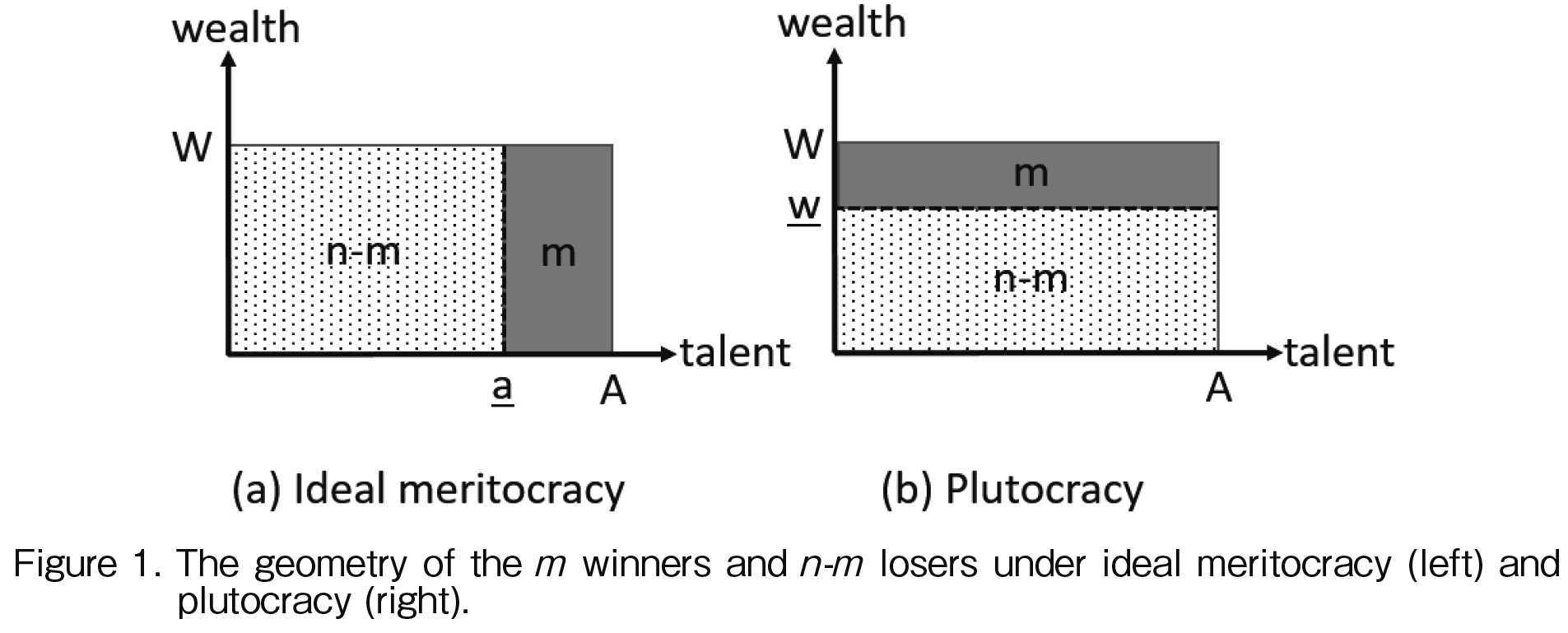
The second baseline case is plutocracy: prize jobs are allocated to the m wealthiest agents without regard to their talent or credentials. In this case too, agents do not invest in credentials. The total talent among the winners is

where 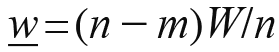 is the wealth of the least-wealthy winner. (See Figure 1b) Evaluating (10) yields
is the wealth of the least-wealthy winner. (See Figure 1b) Evaluating (10) yields

Comparing these two baselines shows that, unsurprisingly, there is less talent employed in prize jobs under plutocracy: T1 (m, n) > T2 (m, n) for all m < n.
3.2@Credentials-based meritocracy without wealth inequality
As a third baseline, consider a credentials-based meritocracy in which all agents are endowed with the same wealth wi = w0>0. In this special case, talent is distributed uniformly among the n agents per the density function
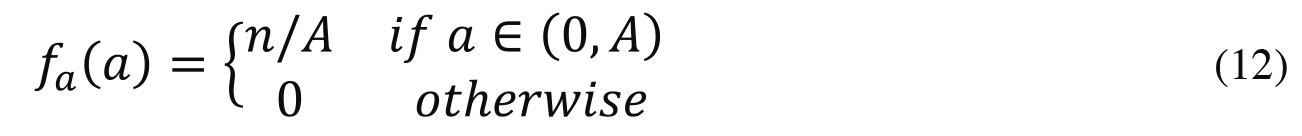 y192Åz
y192Åz
In the absence of wealth inequality, a more-talented agent has a lower utility cost of obtaining any given credential than a less-talented agent. Thus, a credentials-based meritocracy with equally wealthy agents allocates prizes to the m most-talented agents, just like in the pure meritocracy baseline. The total talent among the winners is
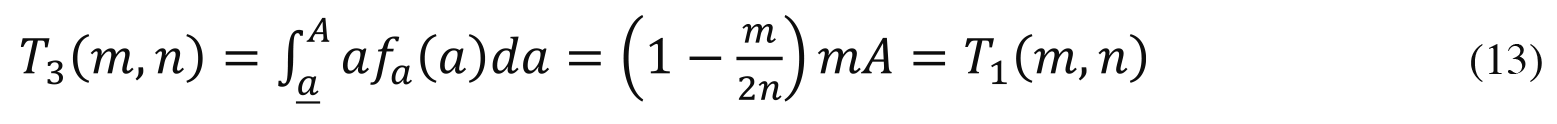
where, as above, 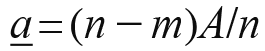 > is the talent of the least-talented winner.
> is the talent of the least-talented winner.
Unlike in the ideal meritocracy baseline, however, employers cannot observe talent directly and thus hire based on credentials. Consequently, agents compete for credentials to signal their talent. Specifically, in equilibrium, each of the m most talented agents invests effort and money to obtain the threshold score defined in (6):

Per (A-5), the effort a winning agent with talent a uses on obtaining credentials in equilibrium is
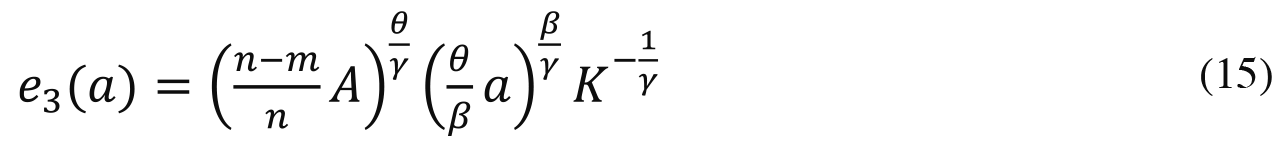
Since (15) is increasing in a, the more talented winners invest more effort than the less talented ones.
Since (15) is independent of w0, raising everyonefs wealth by a given factor has no effect on agentsf effort or the outcome.
Per (A-6), the money a winning agent with talent a uses on obtaining credentials in equilibrium is
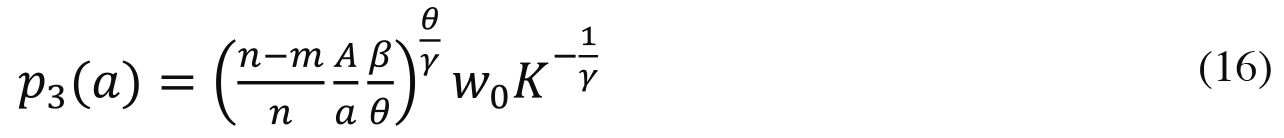
Since (16) is decreasing in a, the more talented winners spend less money on credentials than the less talented ones. Since (16) is linear in w0, raising (lowering) everyonefs wealth by a given factor increases (lowers) the spending on credentials by the same factor.
Per (A-9), the disutility to a winner with talent a in equilibrium is

Since (17) is decreasing in a, the more talented winners sacrifice less utility on credentials than the less-talented ones. Furthermore, since (17) is independent of w0, raising or lowering everyonefs wealth by a given factor has no effect on the disutility of credentials-seeking.
To assess the social cost of credentials competition, let us examine the aggregate disutility of earning y193Åzcredentials as a fraction of the aggregate utility of the prizes. Since each prize has utility 1, the aggregate utility value of all the prizes is m, and the fraction of prize value used up in the competition for credentials is
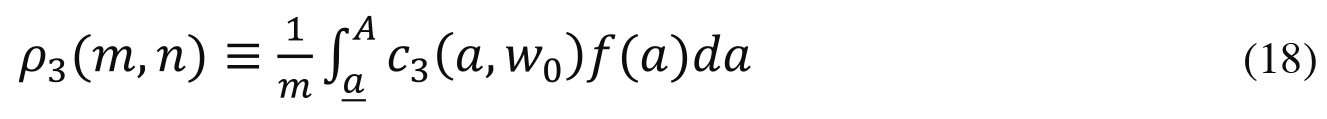
In general (18) reduces to
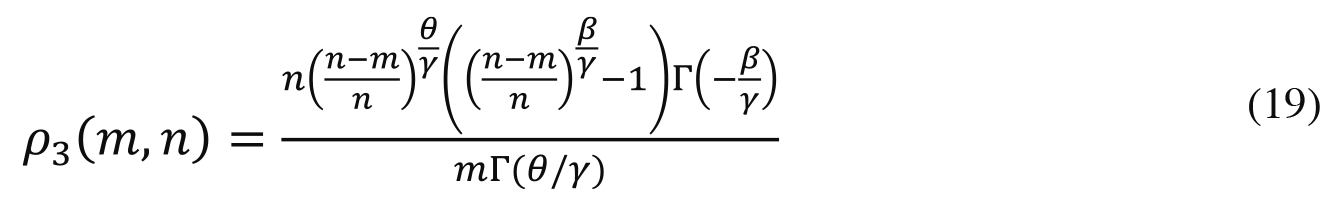
where ¡(E) is the Euler gamma function. If the productivities of effort and money are the same, then (18) reduces to
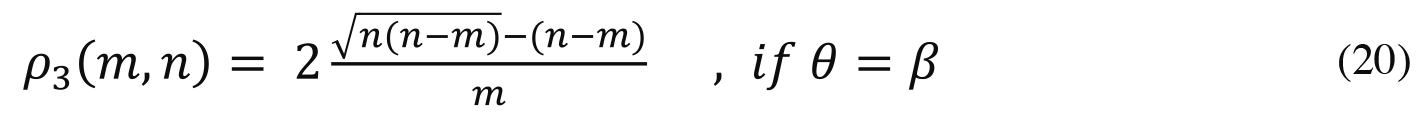
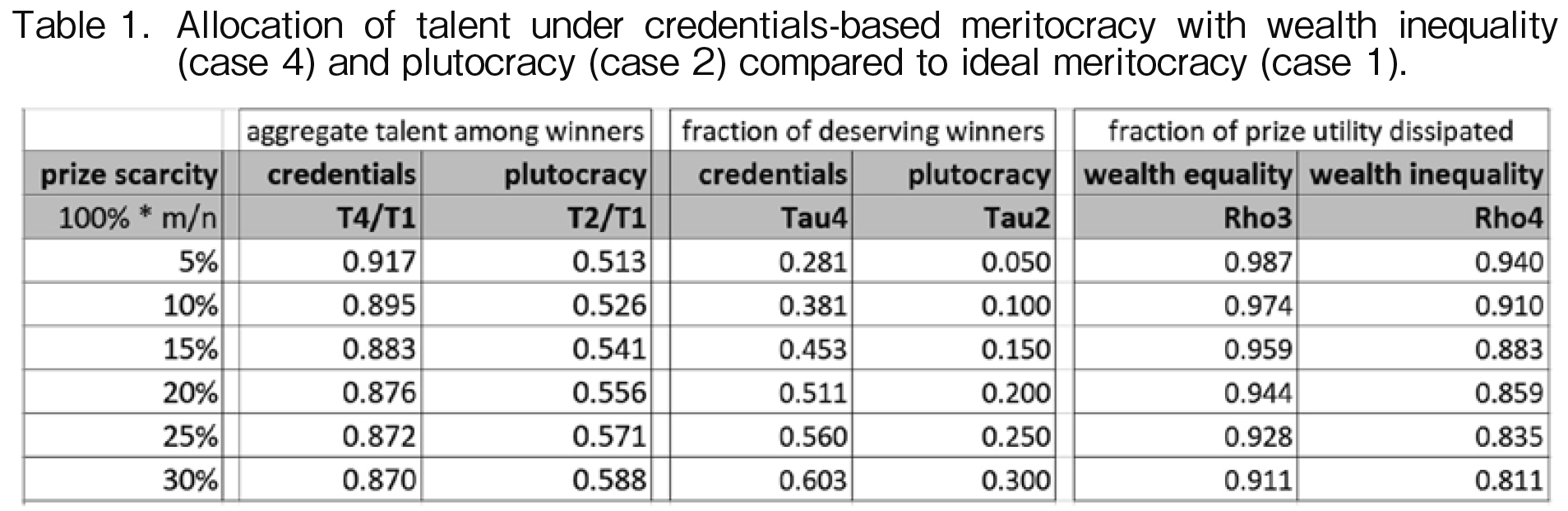
As Figure 2 shows, this fraction approaches 1 as prizes get rare and falls monotonically as the number of prizes increases. To take one point on the middle curve in Figure 2 (see also Table 1): when there are enough prizes for 20 percent of the agents, the winnersf disutility due to credentials-seeking amounts to 94.4 of the utility that the prizes bring them; in other words, less than 6 of the prize utility is not competed away. Thus, in competing for rare prizes the winning agents ante up much of the utility of their prizes. Consequently, ex post the winners as a group are not nearly as much better-off as they may appear to someone who only pays attention to their prizes.
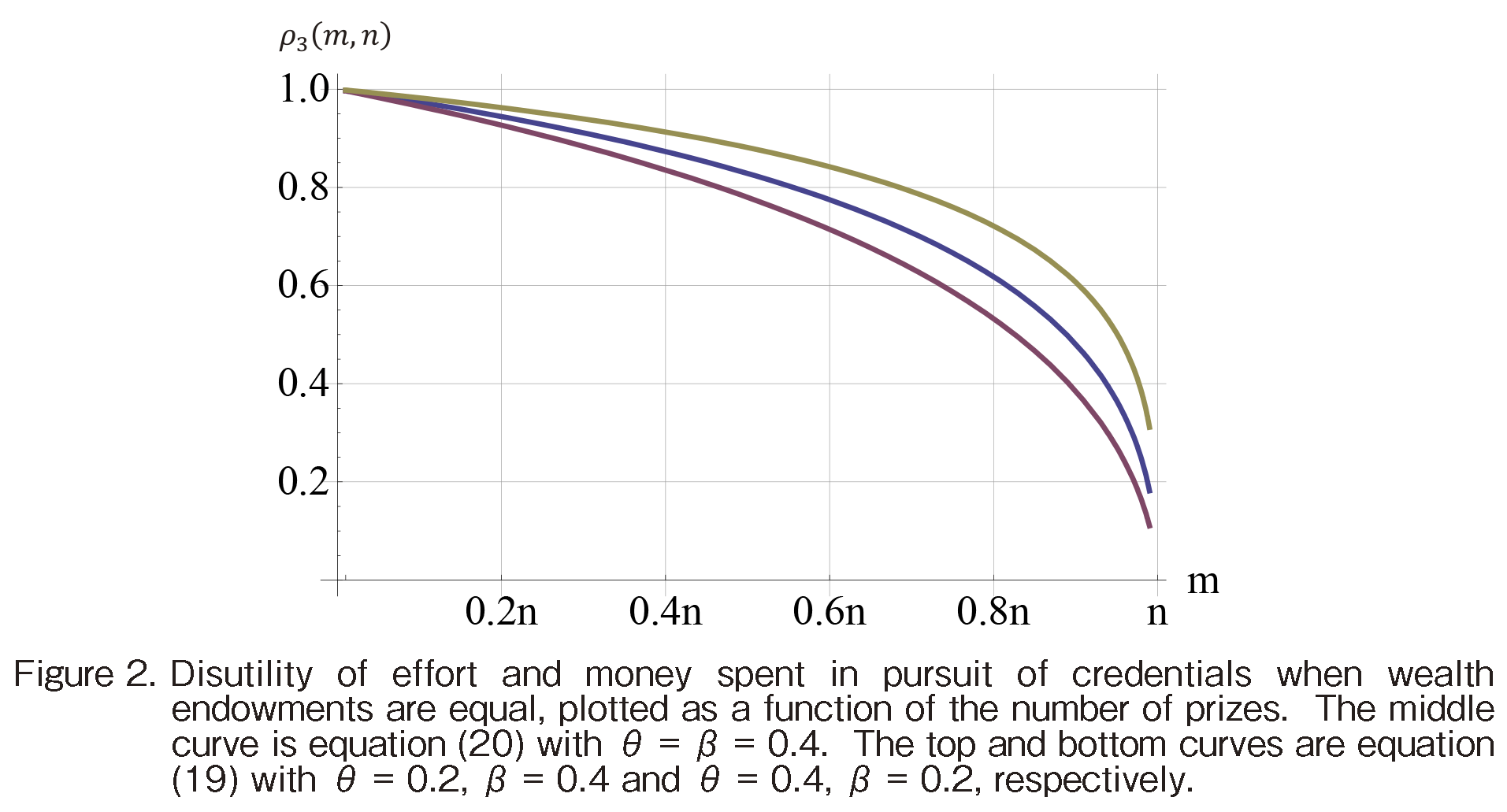
y194Åz
3.3@Credentials-based meritocracy with wealth inequality
Lastly, we turn to a credentials-based meritocracy with heterogeneity in both talent and wealth endowments. Figure 3 shows how the winning and losing agents are distributed on the talent-wealth plane. For a given number of prizes m, the least-talented but most-wealthy winner is the agent with talent a* and wealth W. Extending down and to the right from (a*, W) is the frontier gm(a) separating winners from losers. The subscript on g indicates that there is a family of such frontiers, one for each possible m. Along the frontier lie agents who would obtain zero utility upon obtaining the threshold score t(m) and winning a prize. Since the utility value of the prize is 1, agents along the frontier have endowments (a, gm(a)) that satisfy

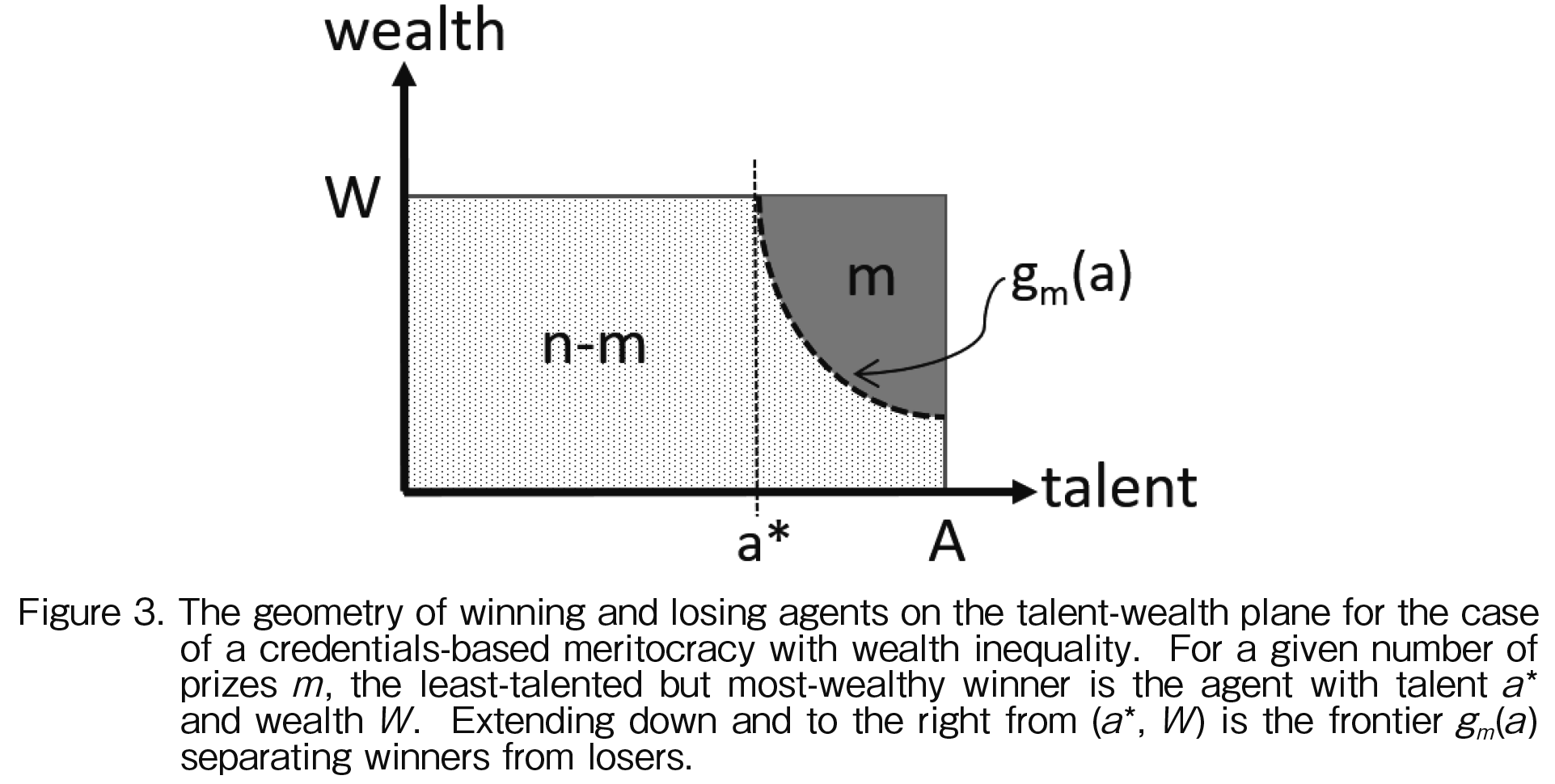
Substituting (6) and using the boundary condition gm (a*)=W shows that the frontier is a hyperbola-like curve given by

The set of winners is thus comprised of those agents who are wealthier and more talented than those who lie along the frontier (22):
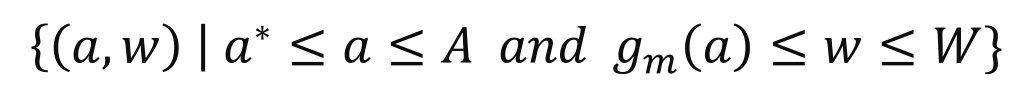
Since the mass of the agents in the area of the winners must sum to m, we can solve for a* using:
y195Åz
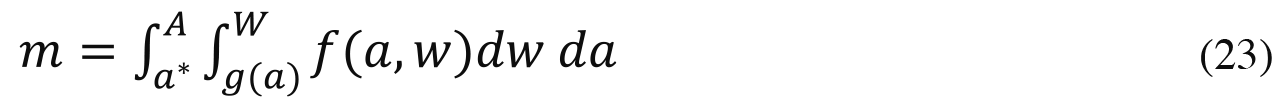
To obtain a closed-form solution, from now on we will assume Æ=À . Solving (23) for a* gives

where

where W-1 is the -1 branch of the Lambert-W function (product logarithm) and e is the base of the natural logarithm.
Substituting (24) into (22) gives the expression for the frontier:

We can now compute the total talent among the winners as follows:
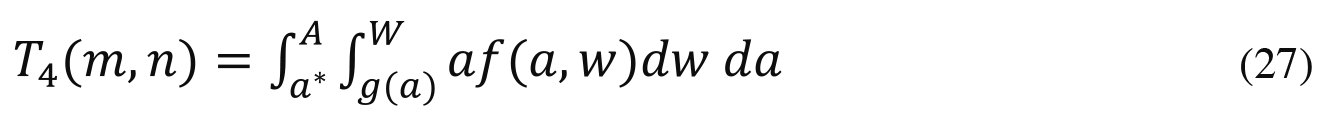
When Æ=À, (27) has the following closed-form solution:
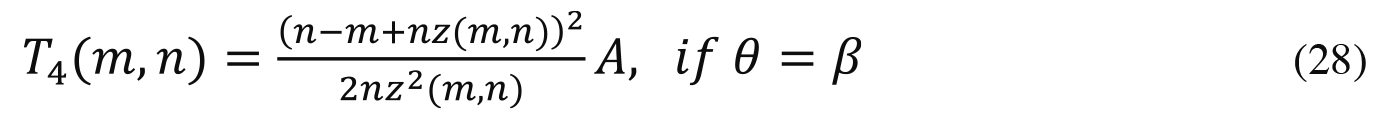
Since (28) does not depend on W,Æ,or À, the total talent among the winners does not depend on the productivities of effort and money or the dispersion of wealth endowments. 3j
In equilibrium when Æ=À, each of the m most talented agents invests effort and money to obtain the threshold score derivable from (6) and (24):
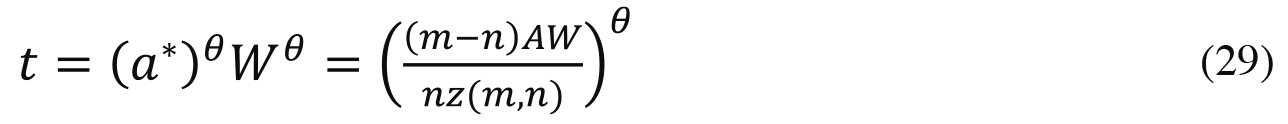
Per (A-5), the effort a winning agent with endowments (a, w) uses on obtaining credentials in equilibrium when Æ=À is
y196Åz
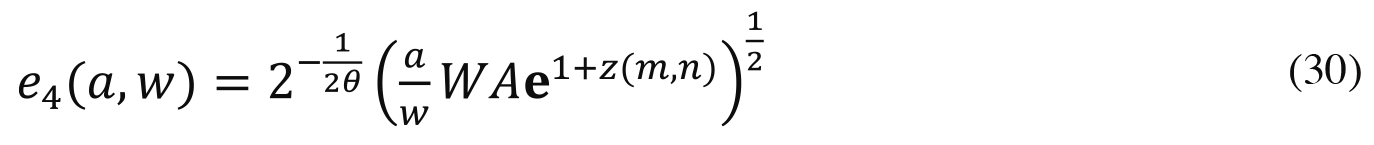
Since (30) is increasing in a and decreasing in w, the more talented (wealthy) winners invest more (less) effort than the less talented (wealthy) ones.
Per (A-6), the money a winning agent with endowments (a, w) uses on obtaining credentials in equilibrium when Æ=À is
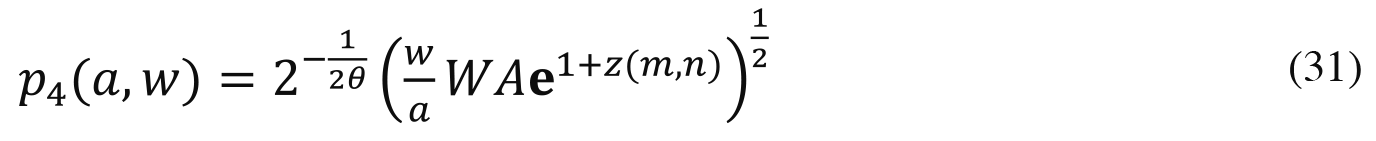
Since (31) is decreasing in a and increasing in w, the more talented (wealthy) winners spend less (more) money on credentials than the less talented (wealthy) ones.
Per (A-9), the disutility to a winning agent with endowments (a, w) in equilibrium when Æ=À is
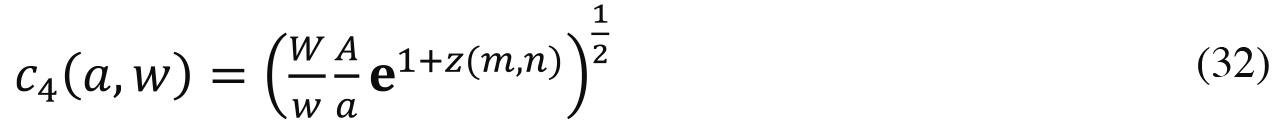
Since (32) is decreasing in a and w, the more talented and the more wealthy winners suffer less disutility in obtaining credentials than the less-talented less-wealthy ones.
To assess the social cost of credentials competition, let us examine the aggregate disutility of earning credentials as a fraction of the aggregate utility of the prizes. Since each prize has utility 1, the aggregate utility value of all the prizes is m, and the fraction of prize utility used up in the competition for credentials is
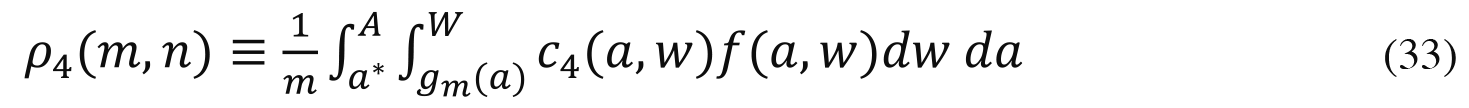
Continuing to assume that productivities of effort and money are the same, (33) reduces to
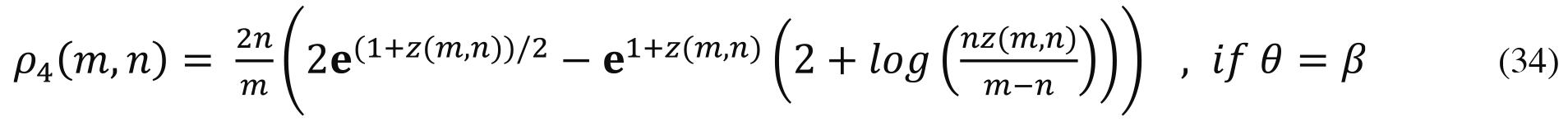
As Figure 4 shows, this fraction approaches 1 as prizes get rare and falls monotonically as the number of prizes increases. To take one point on the middle curve in Figure 4 (see also Table 1): when there are enough prizes for 20 percent of the agents, the winnersf disutility due to credentials-seeking amounts to 85.9 of the utility that the prizes bring them; in other words, only 14.9 of the prize utility is not competed away.
y197Åz
4. Comparative assessment of credentials-based meritocracy
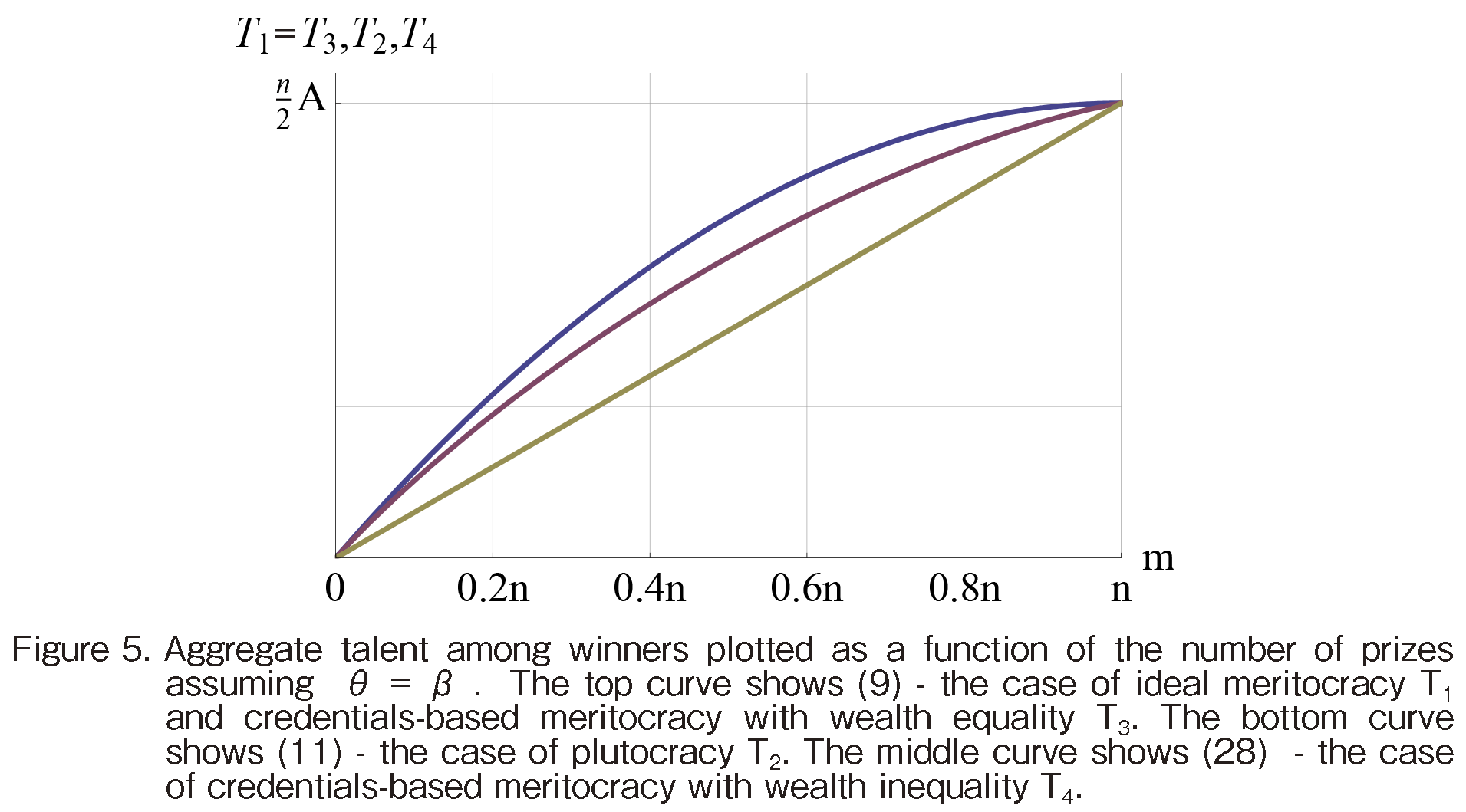
Figure 5 shows how the aggregate talent among winners varies with the number of prizes and across the four selection regimes that we have considered above. For any given number of prizes, an ideal meritocracy and a credentials-based meritocracy without wealth inequality are the best in terms of maximizing talent among the winners. Plutocracy is the worst of the four regimes considered. A credentials-based meritocracy with wealth inequality assembles more talent than a plutocracy but less than an ideal meritocracy.
y198Åz
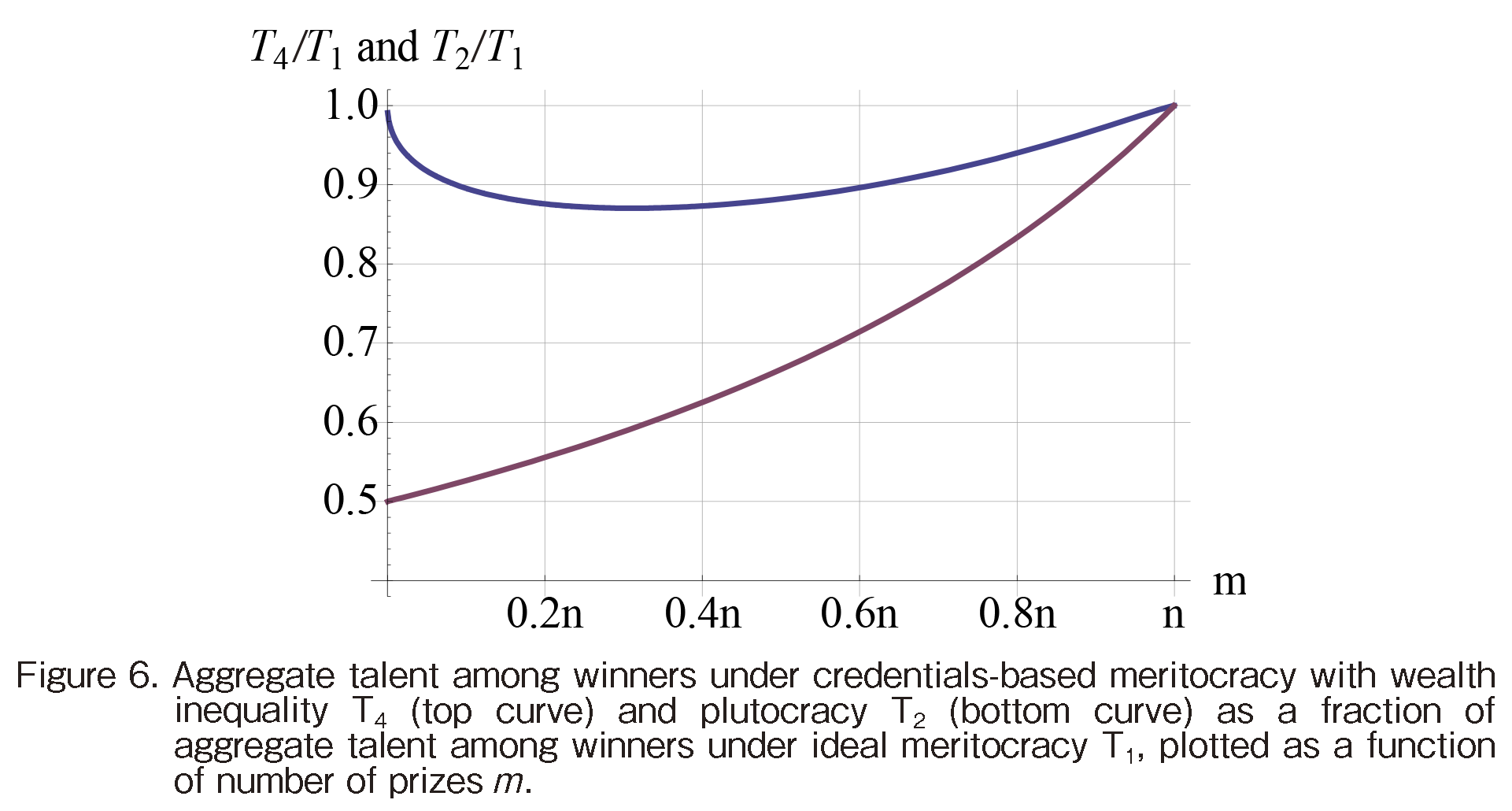
Figure 6 presents another way to examine the difference among the selection regimes in terms of the talent they assemble. It plots the aggregate talent among winners in a plutocracy and a credentials-based meritocracy as a fraction of the aggregate talent among winners in an ideal meritocracy. As Figure 6 and Table 1 show, at its worse, credentials-based meritocracy with wealth inequality assembles about 13 less talent among winners than does an ideal meritocracy. This worst-case occurs when the number of prizes is enough for about 31 of the agents. When prize availability is lower (higher) than 31, the competition is more (less) intense but the total talent among winners comes closer to the outcome under an ideal meritocracy. In the plutocracy baseline, the aggregate talent among winners may be as low as half of a pure meritocracy. The disparity between plutocracy and meritocracy grows as the number of prizes decreases.
One more way to compare allocative performance is to examine the fraction of gdeservingh winners, i.e., the fraction of winners in a plutocracy or credentials-based meritocracy who would have won in an y199Åzideal meritocracy as well. The fraction of deserving winners in a plutocracy is given by the ratio of the two areas shown in Figure 7a:
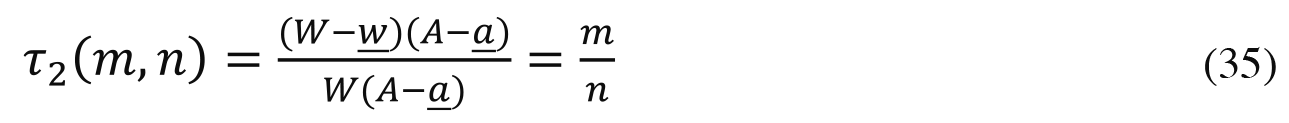
The fraction of deserving winners in a credentials-based meritocracy with wealth inequality is given by the ratio of the two areas shown in Figure 7b:
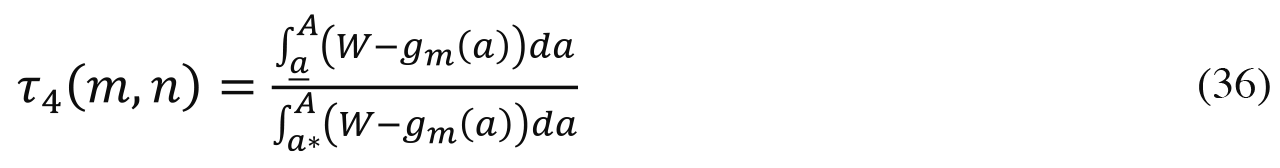
which has the following closed-form solution when Æ=À:
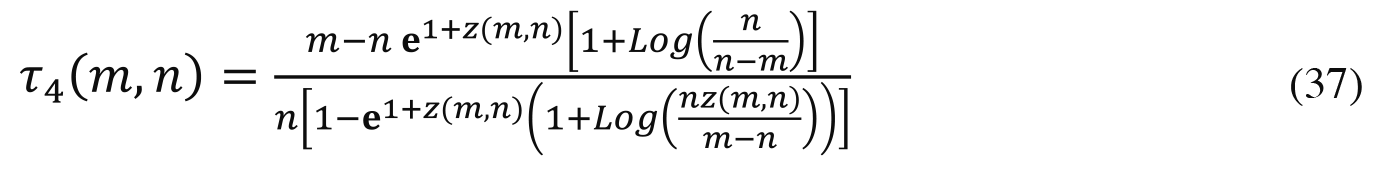
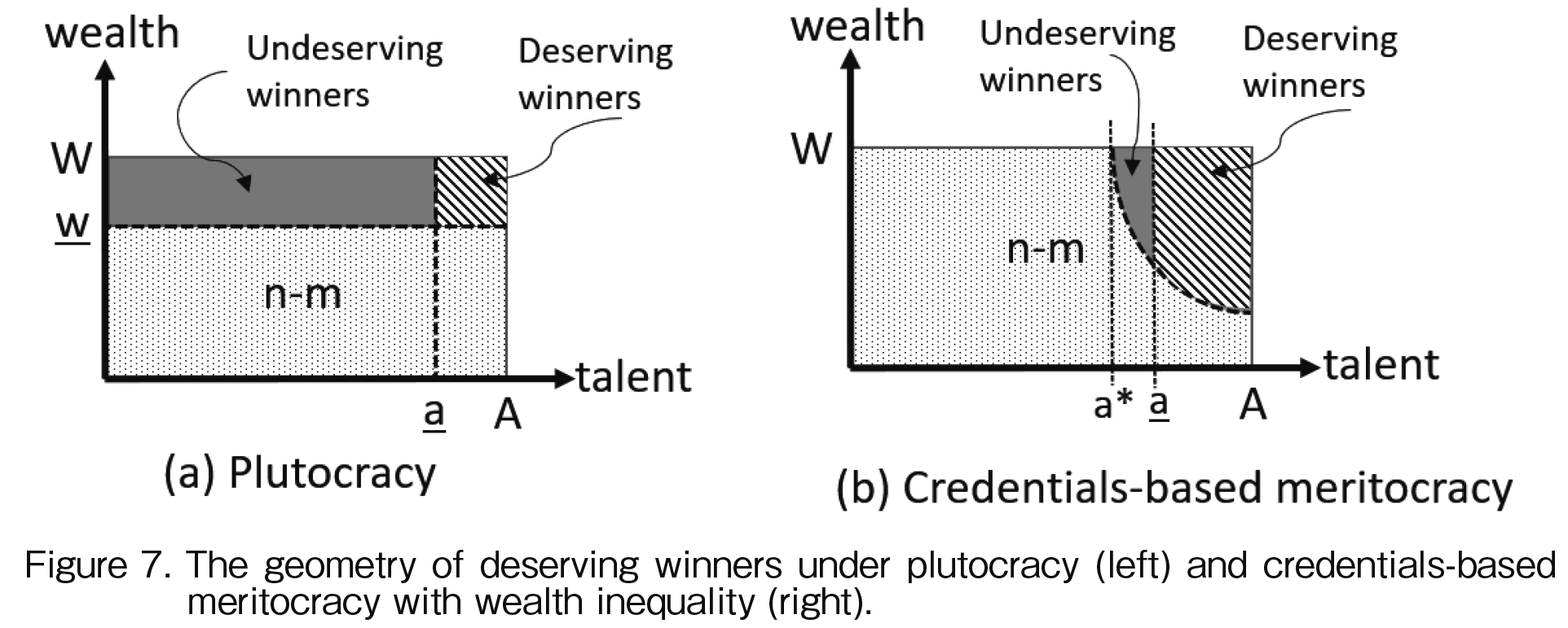
Figure 8 plots (35) and (37) and Table 1 lists some of the values. Consider one sample point: in a credentials-based meritocracy with enough prizes for 20 percent of the agents, only 51.1% among the winners would have won in an ideal meritocracy. Therefore, the remaining 48.9 of the winners win the credentials contest thanks to their wealth, not talent. This reveals the significant extent to which wealth can trump talent in a race for credentials.
y200Åz
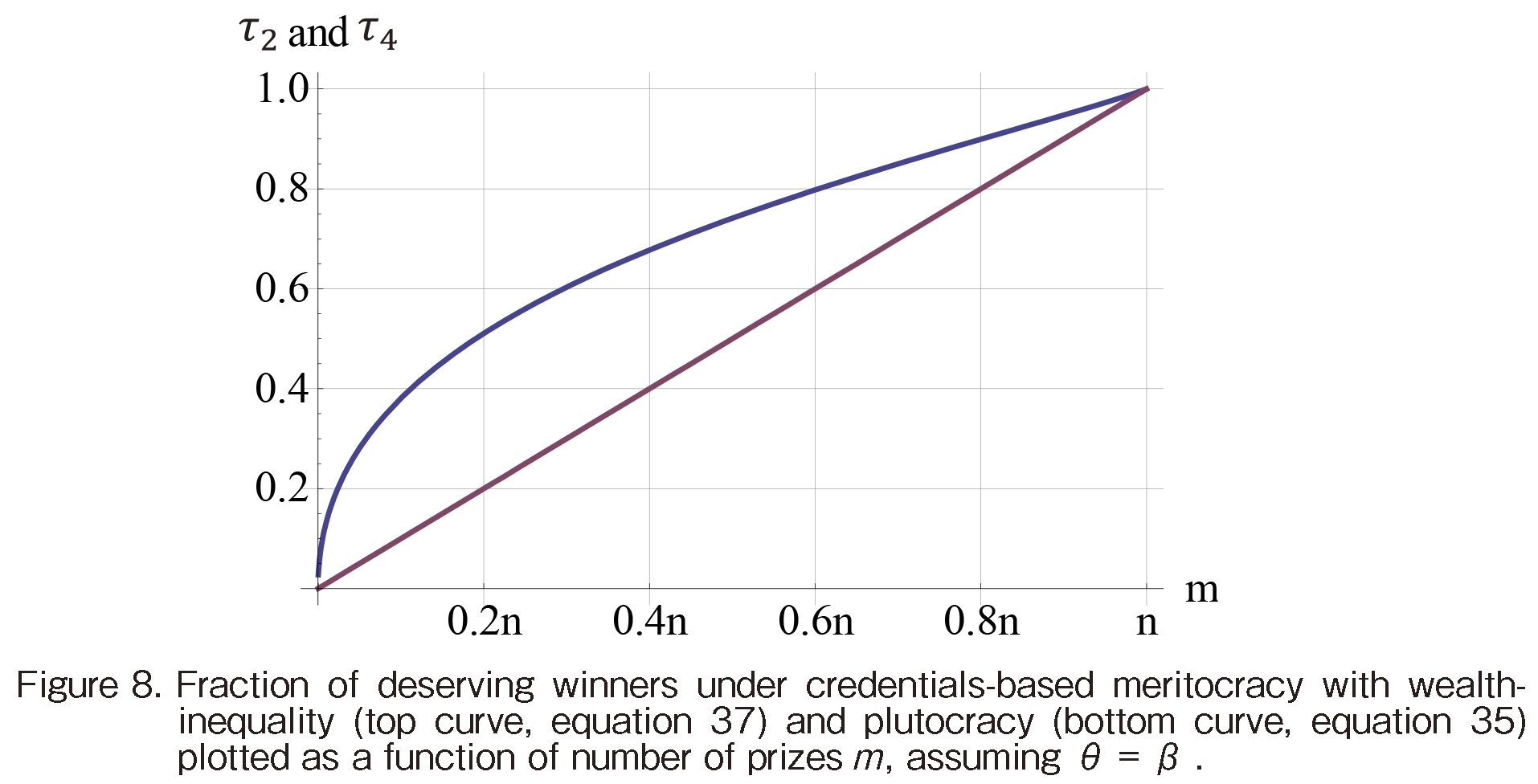
Figure 4 and Table 1 show the fraction of prize utility that winners ante up to obtain credentials. For any given number of prizes and agents, the fraction is higher if all agents have equal wealth endowments than if agents differ in their endowments. Thus, wealth inequality dampens the competition in the sense that winners retain more of the utility of their prizes. Conversely, competition among equally-wealthy agents is more intense in the sense of greater dissipation of prize utility.
This study applied contest theory to examine the costs and distortions of a meritocracy in which candidates for desirable jobs are selected via credentials that the candidates earn using effort and money. The study modeled meritocracy as a multiple-prize game-theoretic contest among agents who are heterogeneously endowed with wealth and talent. Particular attention was given to the effects of wealth inequality and the scarcity of desirable jobs.
Analysis of the model revealed the shape of a frontier curve in talent-wealth space, a battle line along which richer but less-talented agents face off against poorer but more-talented ones. The analysis helped quantify the difference between the set of winners in the credentials contest and the set of most-talented agents who would have been chosen in an ideal meritocracy. The analysis also showed how the cost of racing for credentials varies as a function of prize scarcity.
The findings imply that attempts to implement meritocracy through competition for credentials may give rise instead to a mediocracy tilting toward wealth and with little net gain for the winners. To qualify these findings and obtain better estimates of the costs and distortions, there is a need for additional analysis and computer simulations using a richer framework with diverse prizes and more realistic distributions of talent and wealth endowments. Moreover, there is a need for experiments to ascertain y201Åzthe extent to which behavior by human subjects in multi-prize contest situations matches the theoretical equilibrium upon which this study has been based.
Berg, Ivar (1970) gEducation and Jobs: The Great Training Robberyh Praeger, New York
Dench, Geoff, ed. (2006) gThe Rise and Rise of Meritocracyh Blackwell Publishing, Oxford
Dore, Ronald (1976) gThe Diploma Disease: Education, Qualification, and Developmenth Allen and Unwin, London
Markovits, Daniel (2019) gThe Meritocracy Traph Penguin Press, New York
Rtischev, Dimitry (2020) gIntensity of Effort in Contests with Few or Many Winnersh Gakushuin Economic Papers 57:1-2, 93-108
Sandel, Michael J. (2020) gThe Tyranny of Merith Farrar, Straus and Giroux, New York
Siegel, Ron (2009) gAll-Pay Contestsh Econometrica 77:1, 71-92
Spence, Michael (1973) "Job Market Signaling" Quarterly Journal of Economics 87:3, 355-374
Young, Michael (1959) gThe Rise of the Meritocracy 1870-2033: The New Elite of our Social Evolutionh Random House, New York
Appendix - a model of credentials production
The main model relies on the following specification of how agents rely on their talent and wealth endowments to turn effort and money into credentials.
Each agent can produce any amount of credential s > 0 per a Cobb-Douglas production function
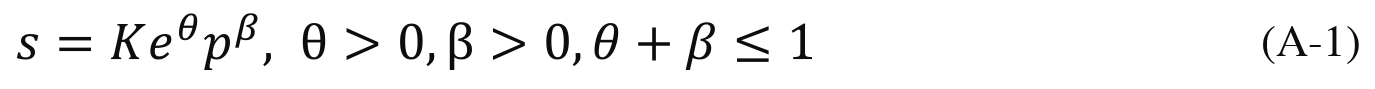
where effort e and money p are the two factors of production and K > 0 is a constant.
Each agent is endowed with talent (or aptitude) a > 0 and wealth w > 0. The disutility of effort is decreasing in talent per

Money used to earn credentials cannot be used for other purposes. The disutility of the foregone consumption is increasing in the amount of money used for credentials and decreasing in wealth per

As discussed in Section 2, since w is a parameter indicating parental socioeconomic capability rather than a stock of money, the case when p > w does not necessarily violate a budget constraint. If p and w were to be interpreted literally as money, then the shortfall p - w may considered as borrowing.
y202Åz
To obtain credential s with the least sacrifice of utility, an agent with talent a and wealth w solves for the minimum utility cost:
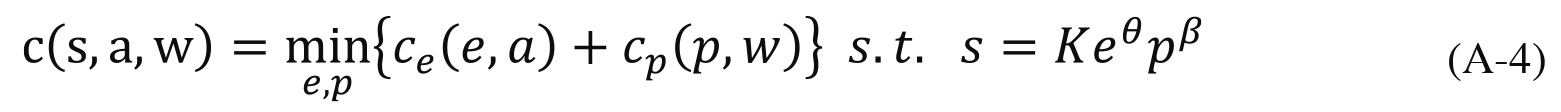
Solving this minimization problem yields the optimal effort and money, respectively:
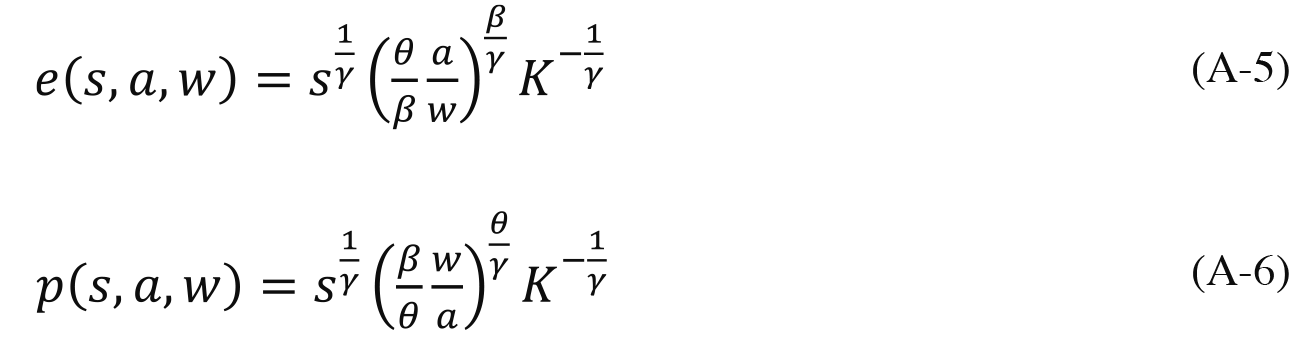
where ÁßÆ + À. Substituting these into (A-2) and (A-3) gives the expression for the minimum utility cost of obtaining credential s :
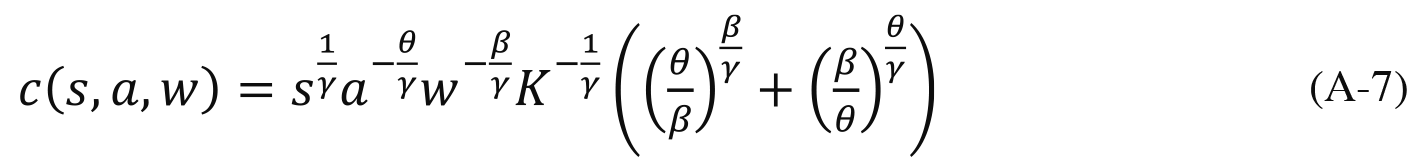
Since the units of the credential s are arbitrary, we can eliminate the complicated constant at the end of the above expression by setting

This rescaling of credentials simplifies (A-7) to

The agents in the model decide how much of a credential to produce based on this utility cost function.