経済学の視点から見た電磁気学の電場メカニズム*
南部 鶴彦
1990年代末から2020年まで約20年間をかけた電力システム改革は,現在電力需給の逼迫と供給の安定性が重大な問題となっている。「改革」の主要なモチーフは地域独占・垂直統合システムを解体する「アンバンドリング」というアイディアに集約されるだろう。これは1980年代からの自由化・民営化・規制緩和という標語の下に,市場メカニズムを導入することによって資源配分の効率性は上昇するという一つの思潮形態である。しかしながら電力の安定的な供給がこのようなリフォームによって可能なのかについて,周到な制度設計がなされていたかには疑問が残る。
本稿では電力の供給とは「電場」の供給であることを電磁気学のフレームワークを紹介しながら明らかにする。電磁気学の体系では「電子」というおよそ経済分析には登場しない主体が,供給システム全体をコントロールすることを数学的に厳密に明らかにしている。したがって正確に理解するには,相応の数学的準備が必要になるが経済学には馴染みのない数学が登場するので,本稿では電場のメカニズムというものを図を使いながら叙述的に記述する。その過程で電場のメカニズムがあるところまでは市場メカニズムと対応可能であるということを示す。しかし同時に安定的な供給を可能にするには,発電からスタートするループが閉回路というサーキットをなしていなければならないという点で,分散型競争メカニズムには適さないことを示そう。最後に全体の記述が結果としてマクスウェルの方程式と呼ばれる電磁気学の基本フレームワークになることを補論という形で述べる。
電力会社が電力というエネルギーを供給できるのは,電子という「もの」の働きがあるからである。ここでは「自由電子」と呼ばれる主体の挙動を,社会的殻に閉じ込められていた人々が「自由人」となって活動するという仕組みと対比させて考える。電子がもたらす電力エネルギーのコスモス(宇宙)は商品を中心とする市場システムと対応させて考えることができる一定の範囲があるからである。第1図はこの関係を極端に模式化したものである。
【228頁】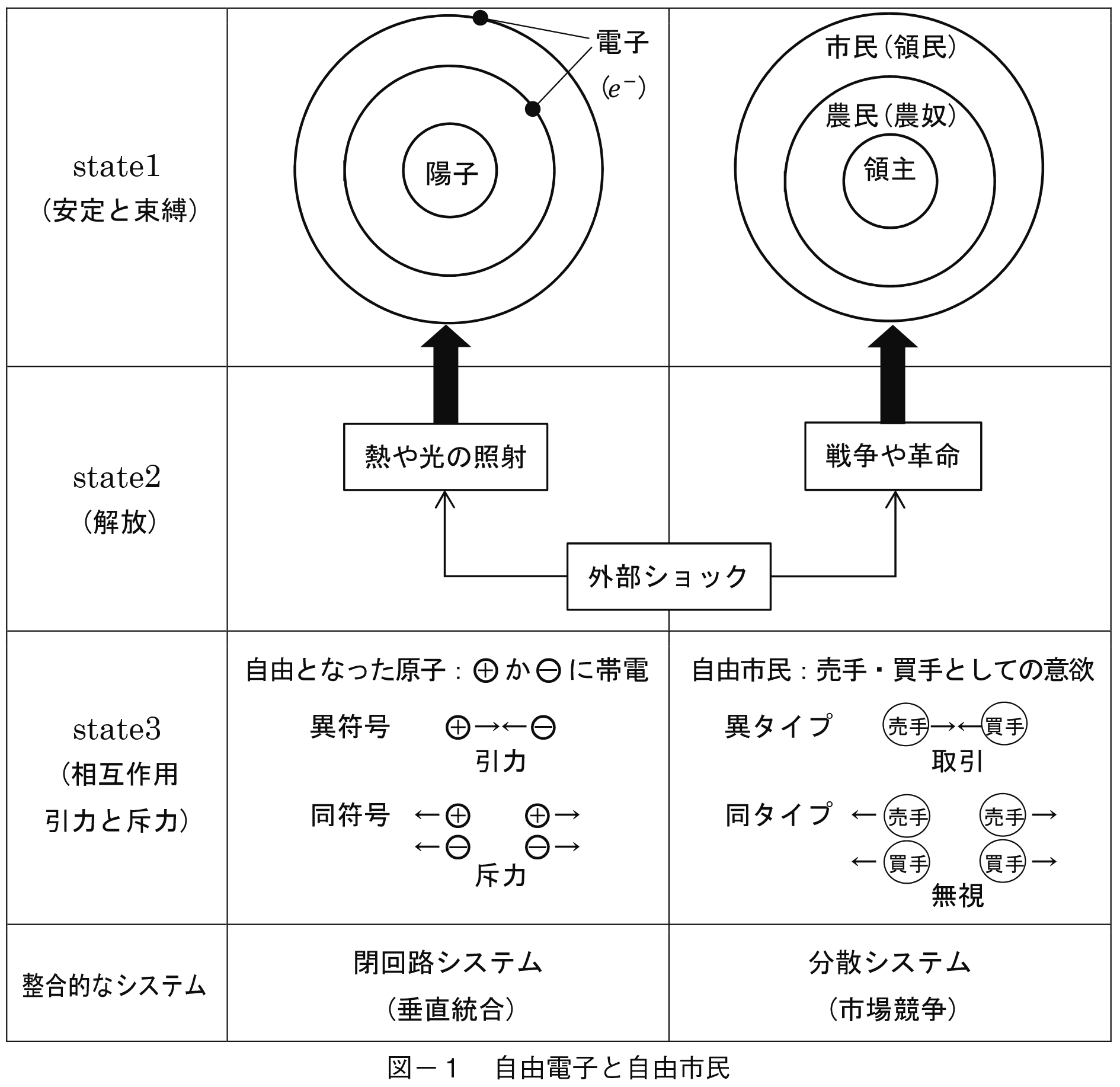
state1からstate3までは電磁気学における電子の挙動を経済学での行動主体のそれと対比したものである。
図−1で電子は原子という殻の中にあって陽子と力のバランスをとりながら軌道上を回転している。もし外部からのショックがなければ軌道上にとどまり続ける。一方封建制下にある人々は領主の支配下にあり,人々はギルド制や農奴制によって職業や移動の自由を束縛されている。いずれも原子や封建制という殻に閉じ込められて現状を変更できない。
state1の均衡状態に対して外部からのショックが与えられるとする。原子に対しては熱や光などの外部圧力があると,原子のもっとも外側の軌道上にある電子への締めつけがゆるくなり【229頁】 電子は自由に出入りできるようになる。このような動きをする電子を自由電子という。一方封建制に対して戦争や革命という外部ショックが与えられると一部の人々は領地内から外部へ脱出する。ここに束縛から切り離された自由な行動の主体が生まれる。
(3−1)自由電子
原子は自由電子の動きによってイオンとなりプラスあるいはマイナスに帯電していて(陽イオンあるいは陰イオン),それ自身が電荷(electric charge)を持っている。chargeとは外部の空間に与える力のことである。この力を電磁気学では仮想的に波及力を持つ力として電気力線と呼んでいる。帯電した素粒子の間には同符号同士は互いに斥け合い,異符号同士は互いに引きつけ合うという実験的事実がある。この性格をあたかも粒子が意思の力を持っているとみなしWillingness To Attract(WTA:引力)とWillingness To Repel(WTR:斥力)があると考えよう。すると粒子間では次のような電気力線が描ける。
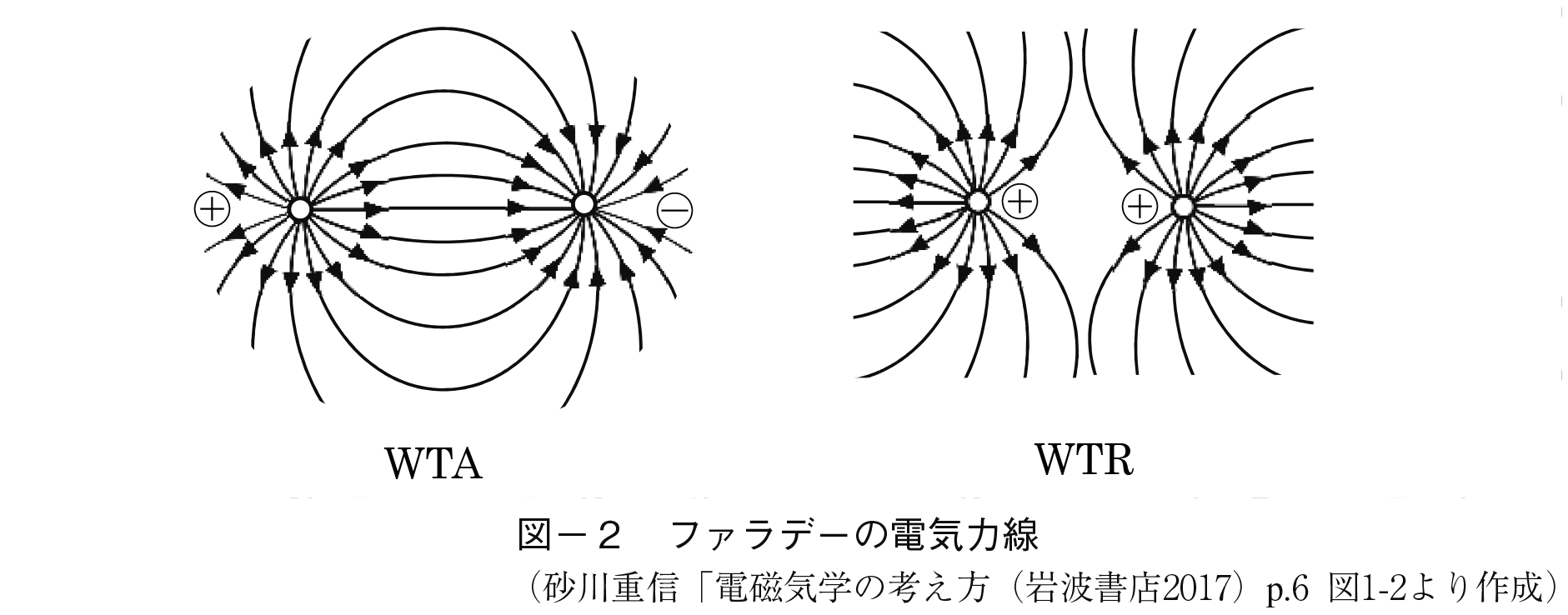
この状況を経済モデルの観点から翻案すると異符号同士では,粒子が互いに取引する意思を持っていると見ることができる。つまり互いに干渉し合う力が相互に働く。物理学的にはこれを「近接作用」と呼んでいる。
(3−2)自由市民
領主の束縛を逃れた人々は都市に集まり,取引によって生活資金を得る。このとき人々は時には買手あるいは売手という取引主体となる。つまり自足的な封建システムを脱却することは旧来得ていたものを何か失い何かを得ることだから陽イオンか陰イオンのような状況と見ることができる。すなわちとある取引において一方はWillingness To Offer(WTO)を持つ売手,他方はWillingness To Pay(WTP)を持つ買手として現れる。
しかしここに貨幣という共通の価値尺度がないときは両者の取引は物々交換にとどまる。
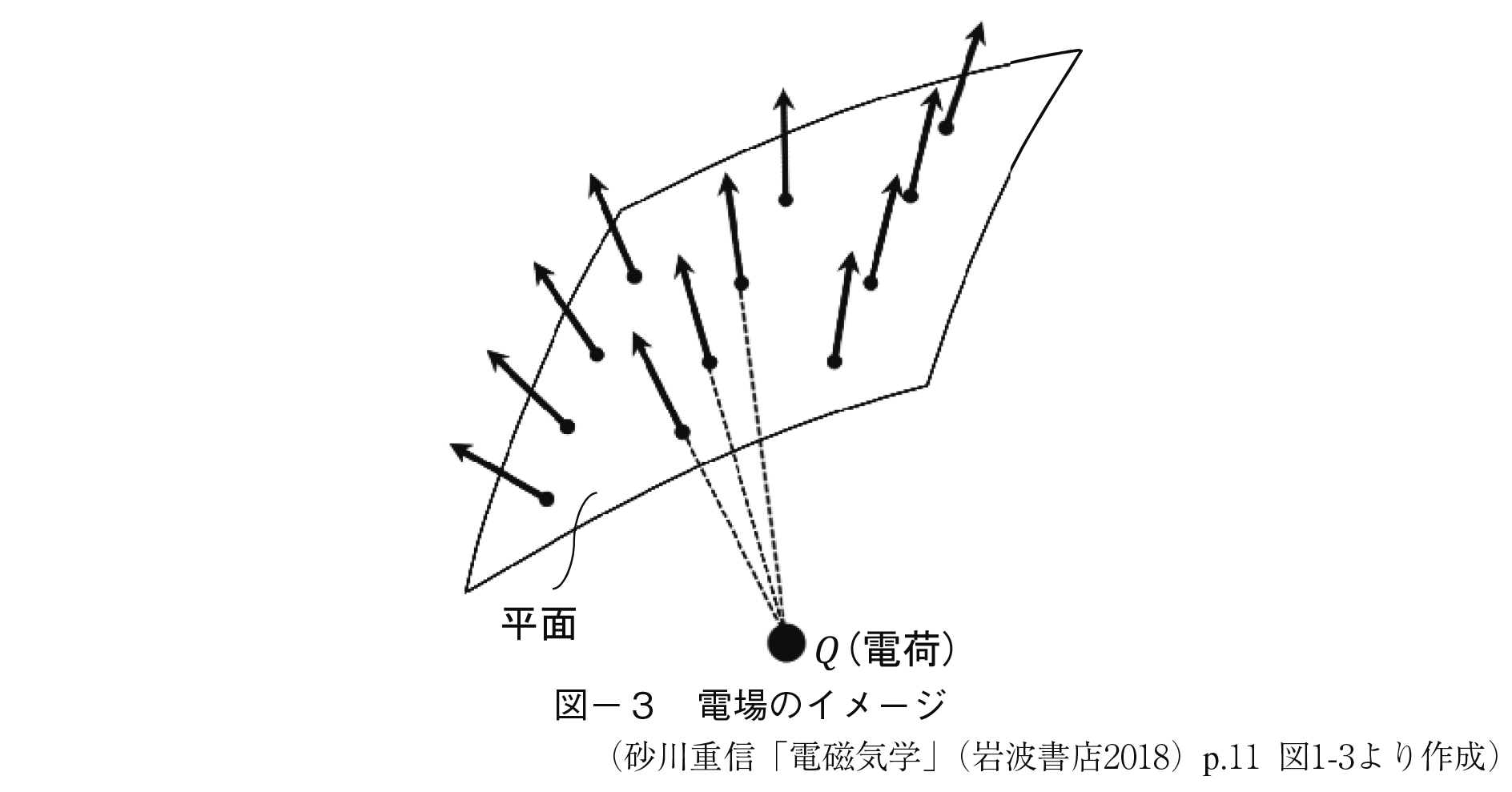
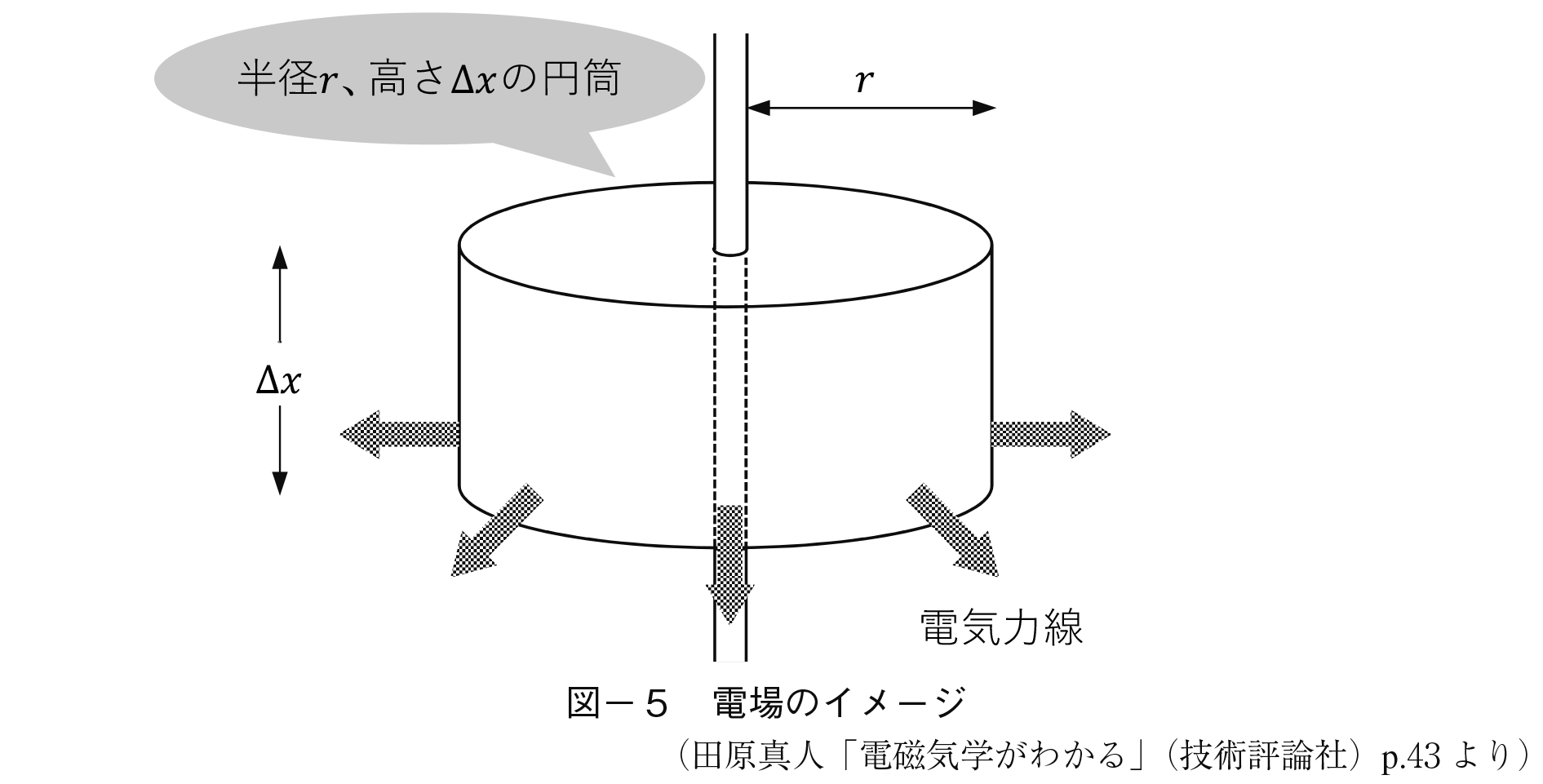
2−1 電磁気学では帯電した粒子間で力が作用する空間を電場(または電界)と呼ぶ。これはあくまでモデル上の概念であるが,この電場に多数の電気力線が通っていると想定する。そしてこの電場の強さは電子の持つ電荷が何本の電気力線を放射しているかによると考える。
一方市場経済が発展した後の財の取引は,ある通貨をニューメレールとして売手と買手が邂逅する。市場では売手も買手も多数いて,電子の例で言えば売手と買手の間に多数の電気力線が出ていることに対応する。
2−2 さてここで電磁気学での電場(デンバ)を経済学の市場(シジョウ)と対応させるためには,電流という概念が必要である。電流について最もよく知られているのは,コイルに磁石を近づけてコイルの中を往復させると電流が流れるというケースであろう。磁石の作る磁場という外からの力に対し,コイルには自ら磁場を作って抵抗する力が働き,そのためにコイル内部から自由電子を飛び出させると説明されている。このプロセスは発電所という電力供給の現場に置き換えると,磁石あるいはコイルの回転のもたらす磁場に対抗して自由電子が発生するというプロセスになる1)。この自由電子は電位差という坂道に誘導されると「波」となって坂道を駆け下りるという不思議な性格がある。この波となって移動する電子が電流である。
【231頁】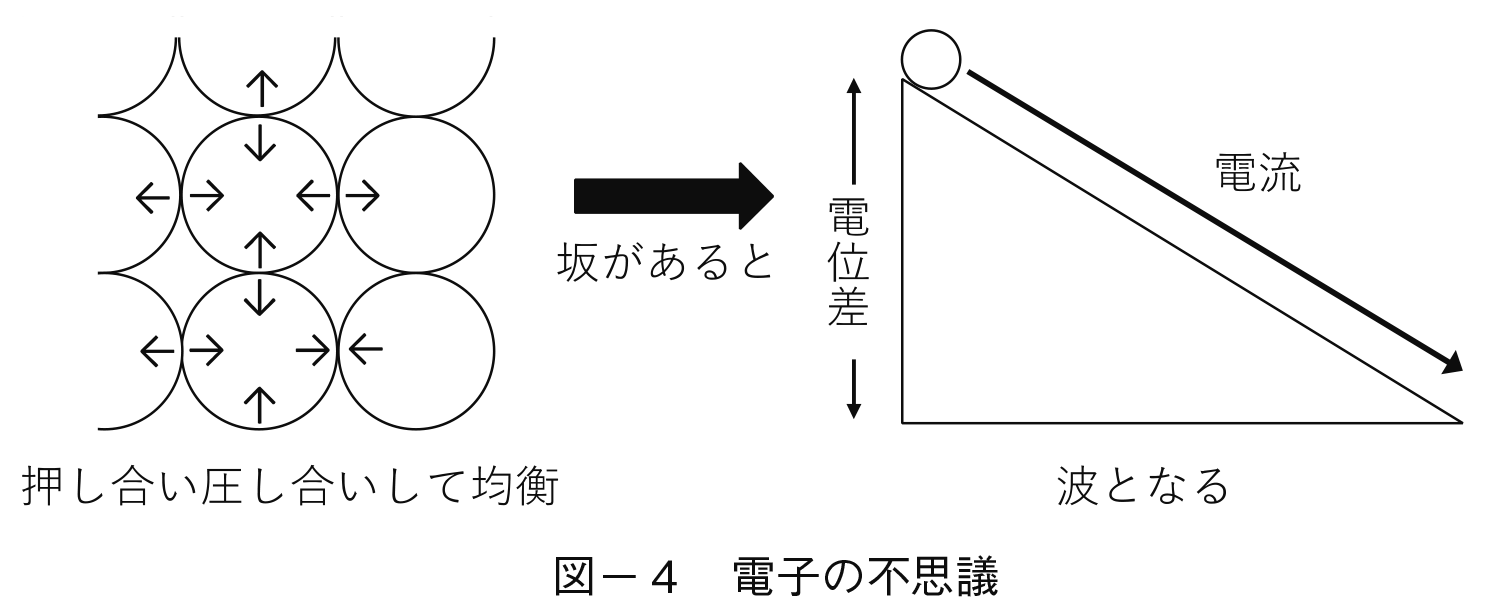
自由電子として飛び出したときは粒子(剛体として扱う)だが,この電子は坂道(電位差)があると波となる。
2−3 さて電流の流れる方向と逆方向に電子は流れる(この点の説明は省略する)。電子はマイナスの電荷を持つが電流の流れと逆方向になるので電流はプラスの電荷を持つと考える2)。そしてこの電子が先述した電場を作るのである(イメージとしては送電線の芯線の周りに四方八方へと電気力線が放射されていると考えれば良い)。
ではこの電場を我々はどのようにして利用しているのだろうか。そのためには,発電・送電・配電とコンセントそして電気機器の複合的な関係を把握しておかなければならない。今回の電力システム改革論議ではこの視点が完全に欠如していたために,安定して強靭な電力システム
【232頁】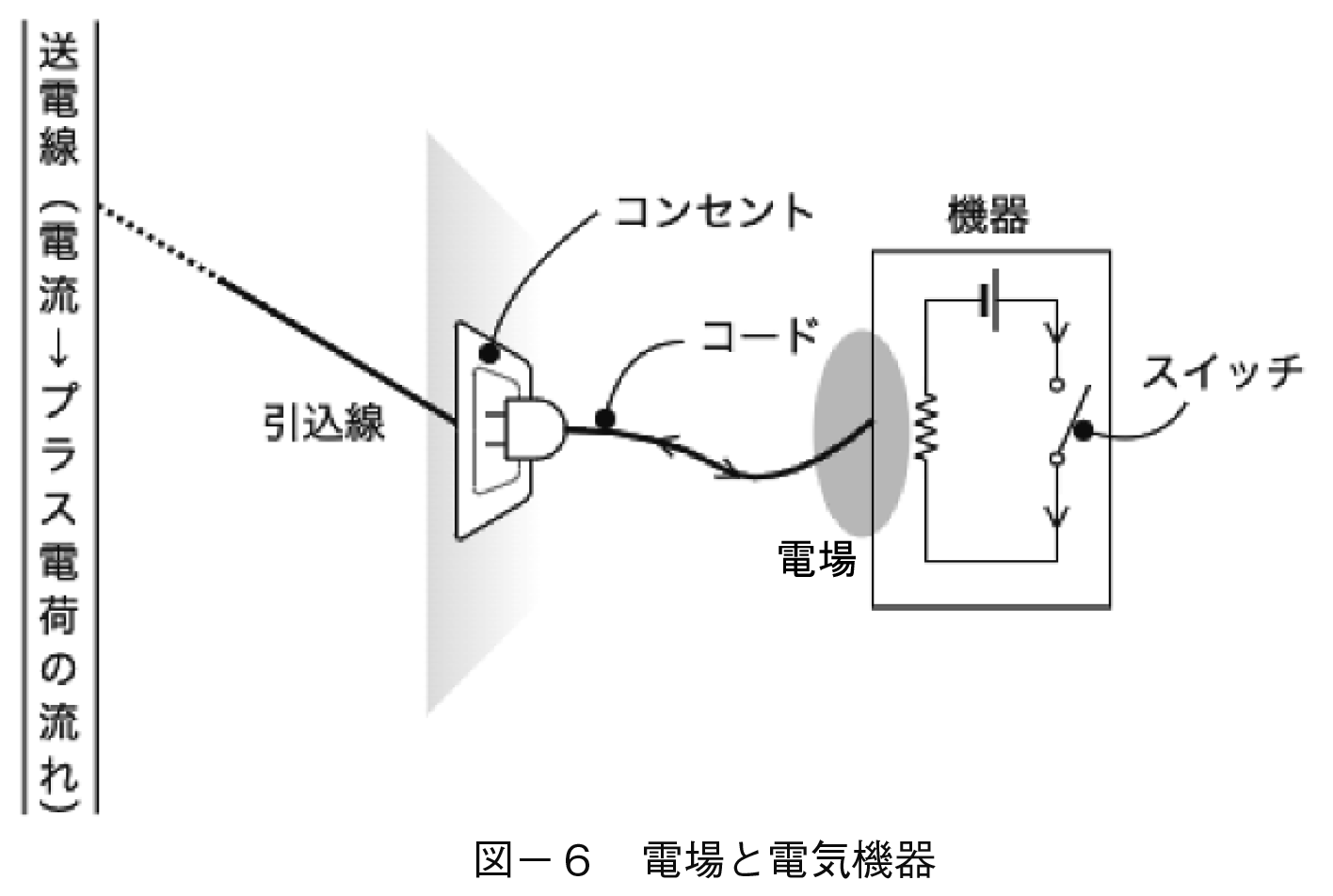
が構築できないのである。
さて電流と逆方向に流れている電子が作る電場が作用するには,コンセントという電流の引込み口がユーザとのインターフェイスの役割を果たしている。
これを図示したのが図−6である。ユーザは購入した機器を用意している。機器を稼働させるにはスイッチをオンにする。すると常時コンセントの外側で待機している電流が引き込めて,電子が電場を作るのでこの外部の電子は機器内の(いわば眠っている)電子に近接作用を与える。電子はここで励起(excite)され,機器ごとに決まっている定格の電圧Vという坂道を巡って電流Iが流れる。これによって周知のように仕事W(ワット)がなされる。
W=VI
この仕事をさせるのは正確に言えば,高圧線と呼ばれている送電線から分岐して電柱上にある,柱上変圧器(トランス)を通じて流れる電流によってである。このトランスから図−6の引込線を通ってコンセントまで電流を送る部分は配電と呼ばれる。つまり送電の端末部門が配電であって両者は一体になってユーザへ電場を「届ける」のである。
このプロセスが電力産業の「流通」を形成している。この点を認識することは極めて重要なので,図−1へ戻って自由市民が行う経済活動と対比してみよう。現代的な市場取引が成立するには,買手と売手との間に取引するインセンティブがある(粒子間の引力のような)だけでなく,共通の交換単位(ニュメレール)−貨幣−が必要である。もし貨幣が存在しないと,売手と買手の双方に取引の意思があっても取引は物に交換になるから,両者の間で交換される「もの」の相対比率が最終的に一致しない限り取引の合意は達成されないであろう。
しかし貨幣というニュメレールが登場すると,売手と買手の供給意欲(WTO)と支払い意【233頁】 欲(WTP)が市場で供給曲線と需要曲線に集計される。つまり貨幣が売手と買手のインターフェイスとなり両者の合意が得られる。この合意形成の「場」が市場である。同時に市場での需給は常に一致するわけではないから,売れ残り(超過供給)や買い損じ(超過需要)が生まれる。この不一致分は時間をかけて調整される必要がある。つまり在庫という商品の保存機構が生まれ在庫は正(超過供給)にも負(超過需要)にもなる。この調整機能を担当するのが流通である。
以上のような通常の「市場」を通じた取引では一瞬にして「売る」量と「買う」量が一致することはないのに対し,電力市場では電流が流れると瞬時に電場が生まれ機器の作動によって「仕事」つまりユーザにとっての効用(スイッチをオンにするという一動作について見れば限界効用)が生まれる。一瞬の電流の働きは,経済的に言えば限界費用に相当する。つまり限界効用と送電の限界費用が一致するのだがそこには通常の意味での流通機構が果たす需給調整メカニズムはない3)。もちろん「仕事」をさせるタイミングを事前の契約によって選ぶという工夫は可能である。季時別料金という制度は古くから存在している。しかしその料金の方は契約によって決定されているとしても,電場が瞬時に発生するときの限界費用はその瞬間でしか決まらないので,事前に限界効用と限界費用を一致させるという効率性を保証するものではない。(リアルタイム・プライシングがそのような機能を持つと誤解されているが,リアルタイムに発生する需要に対する供給の限界費用は常に事後的にしか決まらない。)
「電気が家庭や工場に届く」までのプロセスを俯瞰したのが図−7である。これによって電力は複合的な技術の組み合わせから成り立っていて,通常の商品のように物理学の力学が適用できる範囲を超えていることがわかる。
電力の供給はまず電源の選択という経済的な活動からスタートする(これ以外に安全保障という要素も付け加わる)。選ばれた電源はボイラーからタービンを経て発電機で自由電子を生産するが,この過程までは力学の原理に従う。もちろん,太陽光発電や風力発電もこの物理的プロセスに従う。力学の世界は物理学では「マクロ」とも呼ばれるが,それは対象が”visible”なものだからである。
【234頁】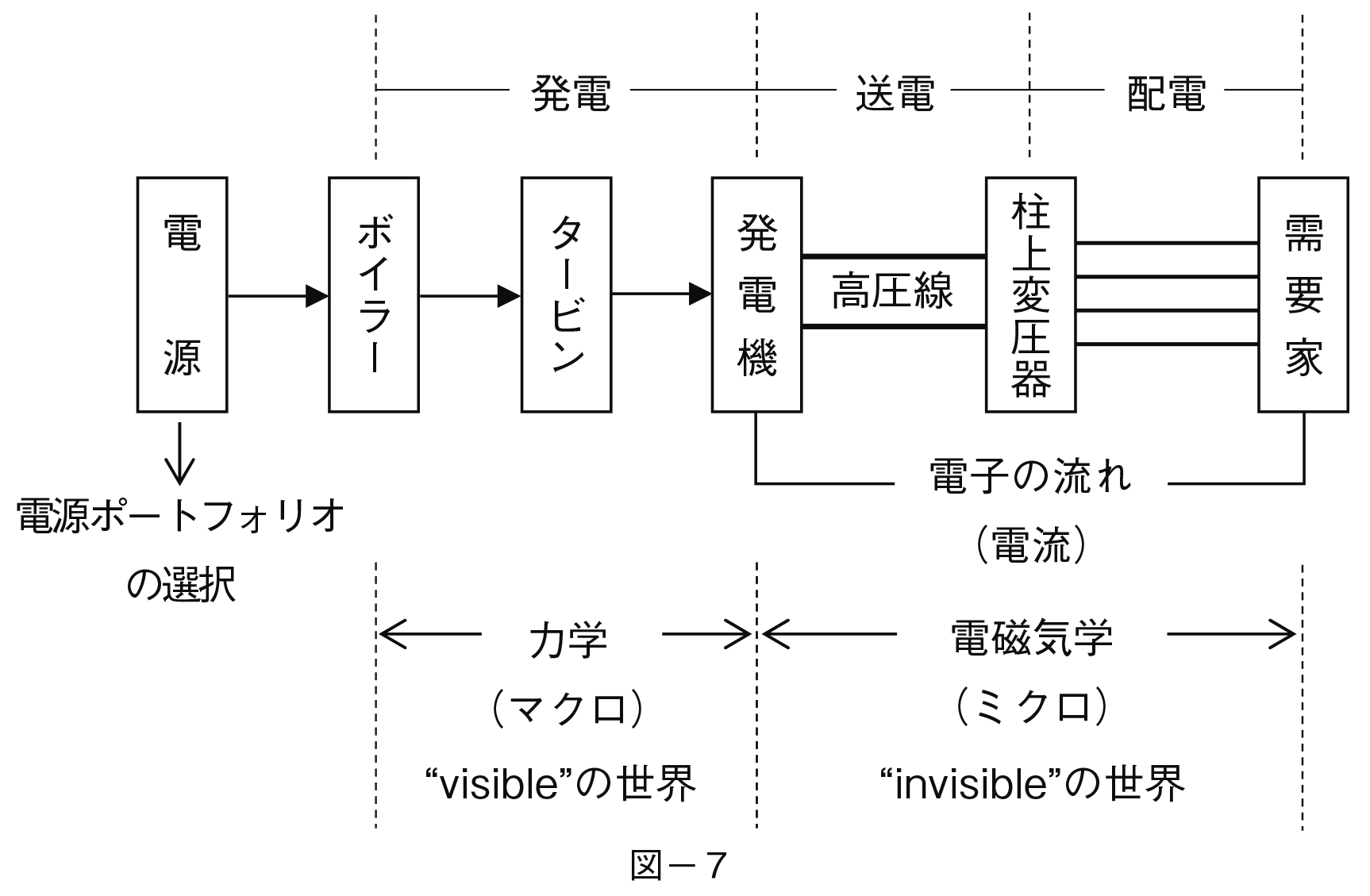
ところが発電機から自由電子が飛び出して以降は電子という”invisible”なものを対象とする電磁気学の世界(更にその奥には量子力学がある)に入る。そして電子の挙動は既に述べたように力学では取り扱いできない分野である。
電力事業の制度設計にとってアンバンドリング(unbundling)という手段が電力産業の改革に有効ではないかというアイディアは1980年代から主流となった。すなわち発電・送電・配電という3部門を切り離し,それぞれ市場メカニズムに委ねるというアイディアである。もし送電と配電という供給プロセスが物理学的に力学系の世界に居するなら,これも一案であろう。しかし既に見たように送電と配電とはシームレスに一体化しているもので,これを無理に切り離せば発電から需要家まで電場を光速で送るという事業は極めて困難となるだろう。旧来の垂直統合システムでは”command and control”(給電指令)という形でこれを実現してきた。これに対してアンバンドリング後には,日本では「広域機関(電力広域的運営推進機関)」がこれを受け持つことになっているが,この寄り合い世帯が以前より効率的が否かは今後検証すべき大きな課題である。
ボイラーから発電機までのプロセスは多種多様な工夫によって発電コストを最小化する努力が19世紀から一貫してなされてきたし,電源は化石燃料から再生可能エネルギーまで革新が続いている。発電という部門は,多数の発電事業者が競合しコストの最小化(利潤の最大化)を達成できる分野である4)。したがってこの分野を全体プロセスから分離することには意味がある(とは言え多くの問題があることは後述する)。
電力供給はユーザとして電気機器(electric equipment)を保有する顧客が存在しなければ市場は成り立たないし,機器は電力が常時使用可能でなければ保有する意味がない。つまり両者には決定的な相互依存関係がある(個別的には蓄電によってこれをバイパスできる。しかし全国大での電力ネットワークにはならない)。これを共軛(conjugate)な関係と呼ぶが,その経済的意味を極めて単純な数学的形式で理解することも可能であろう。
前述のように電力供給の電場メカニズムは力学系の物理学の外にある。一方電気機器は生産・消費ともに力学の世界にある。このような完全に異質なアクティビティを統合して表現するのに共役な複素数が利用できる。
例えば力学に支配される機器の供給する付加価値をa,電磁気学に支配される電力供給の資産価値をbとする。共役関係があるときa,bは
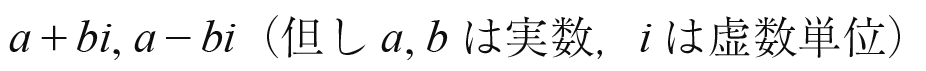
で表現される。共役関係があるとき
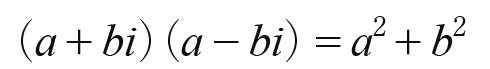
が成り立つ。これの絶対値|h|は
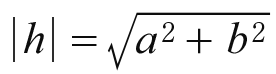
で定義される。
|h|はaとbとがお互いに作用し合っているときの全体の価値を表すものと見ることができる。そして
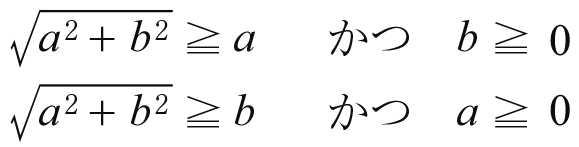
だから共役関係のもたらす価値はaのみあるいはbのみ(つまり電力供給と電気機器を分離したときの単独の付加価値)よりも大きい。
つまり
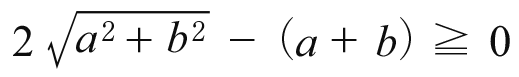
又は
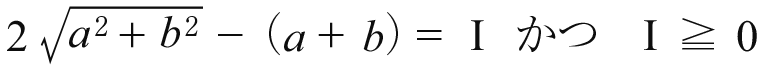
が成り立つ。
これは電力供給において停電が甚大な意味を持つことを示している。停電とはbが切断されることによってaの持つ付加価値が失われることを意味する。(停電は例えば交通システムの停止のような社会的混乱をもたらすが,それは外見上のことに過ぎない)。その本質は電気機器が作用しないことつまりそれに依存している現代社会の全マクロ的な社会的損失をもたらすのである。
したがって電力の安定的な供給は,社会にとって必須の条件となる。すなわち常時コンセントさえあれば電場が供給される条件は何かを次に明らかにしなければならない。もちろん将来,分散型電源や蓄電池によっていつでもどこでも電力が入手できるという技術革新があれば,この条件は緩和されるだろう。これは本稿では分析の視界に入れていない。
電流が流れている(つまり電子が反対方向に流れている)という状態が存在するには,次の条件が必要である。電子は電位差という坂道を「波」となって移動するのだが,この電流は発電された原点に光速で回帰するという条件がなければ,連続的に供給されることはない。つまり次図のように電流はサーキット(閉じられた回路)をなしていなければ,我々は電気を利用することはできない。いつでも電気を我々が使えるということは,電磁気学的に言えばポテンシャル・エネルギーが保存される条件が必要であり,それは任意の閉じた回路(経路)を成しているサーキットが用意されていなければならないのである。直観的に言えば発電所というものが絶え間なく電力(電子)を送り出すポンプの役割を果たしていなければならない。
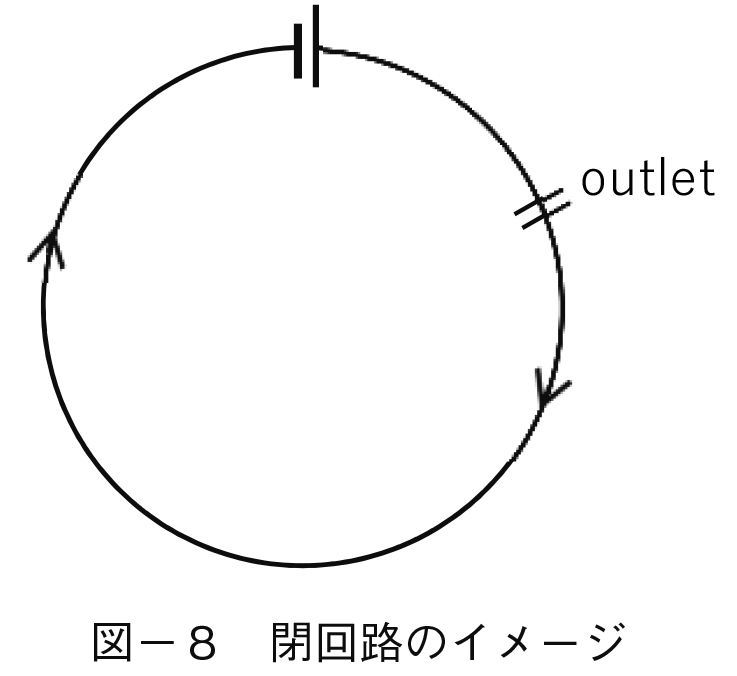
さらにユーザが電力を取り出すコンセント(outlet)に待機している電場は光速で移動している。つまりスイッチをオンにして機器を作動させる「きっかけ」としての電場は一瞬にして通り過ぎるのである。このことを「電気は保存できない」とか電力供給は「同時同量」が必要だとか表現することがある。しかしこのような表現には程度の差を許すような曖昧さがある。電場が光速で移動するという物理法則は変えようがない。
厳密に言えば以上の説明は静電気に関するエネルギー・ポテンシャルの説明である。より具体的にはいつでも定量の電気が流れている状態を保つためには,定常電流の保存則が必要だが,これはサーキットが閉回路になっているという前述の必要条件から推測できるであろう。
定常電流が流れている状態とは,経済的モデルで見れば次のように表現できる。電力の需要には時間差があって需要が集中するピーク時と需要が閑散となるオフピーク時がある。電力企業がこのどちらの需要にも対応できるように電場を供給するということが,定常電流を流すということである。ピーク時には相対的にコストの高い発電所も動員せねばならないので供給の限界費用MC1はオフピーク時のベース電源だけで供給するときの限界費用MC2よりも高くなる。
そこで定常電流が流れ,需給が均衡するという状況は次図のように描ける。
【237頁】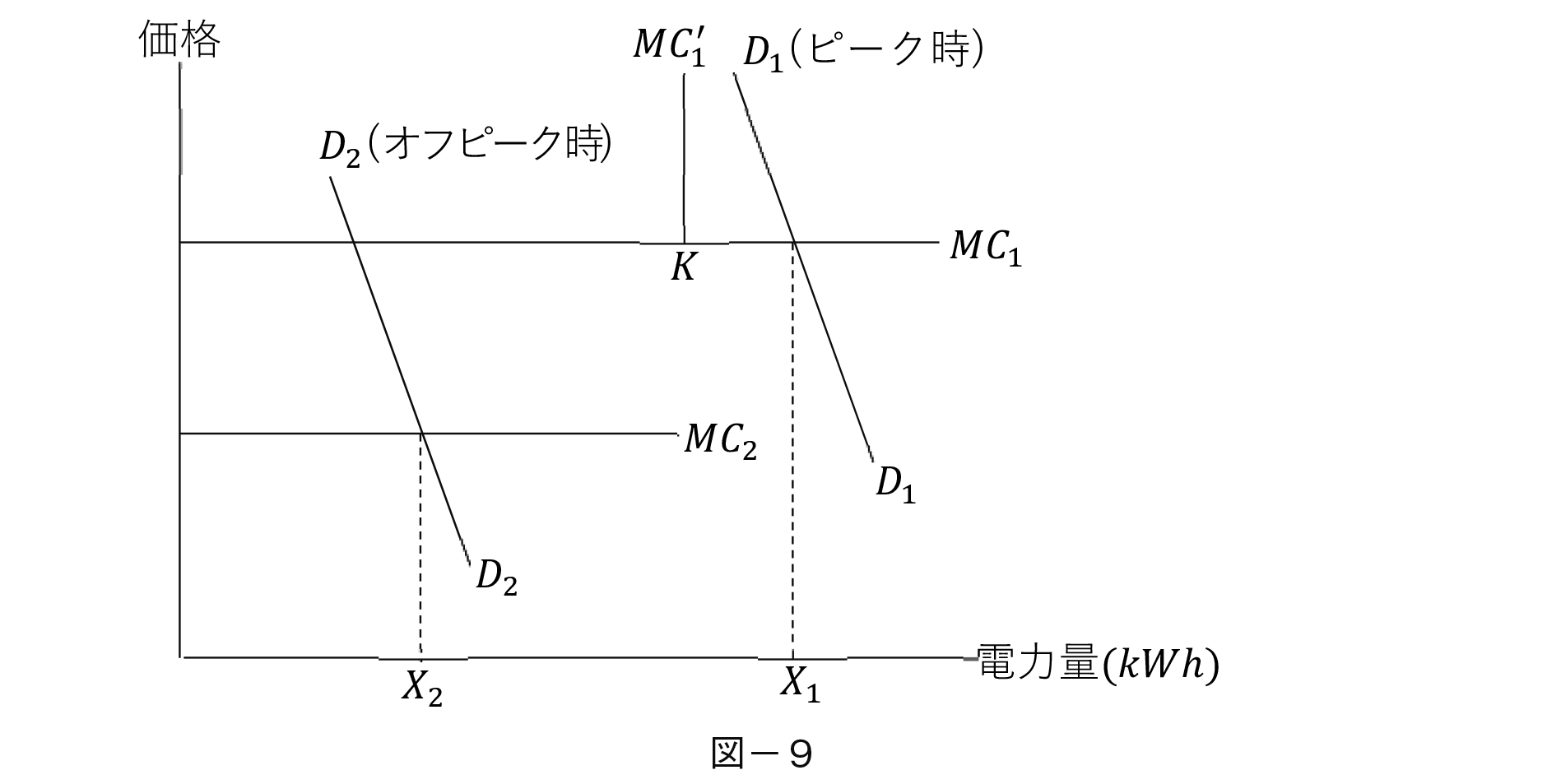
図のD1 D1とD2 D2はピーク時とオフピーク時の需要関数,X1とX2とは需給均衡量である。定常電流が不足するときは,例えばMC1でMC1がK点で垂直なMC1‘となるようなことが起こる。このとき停電は避けられない。
以上の分析を踏まえて,電力の供給というビジネスが通常の商品の供給とどのように異なるか比較してみよう。
電力産業とは結局のところ電場産業である。電場は光速で移動する以上,そのサービスつまり「近接作用」を保存することはできない。つまり電力商品とは一瞬にして消えてしまう「作用」というものの供給を行っている。ここで全く在庫ができない商品を供給するとしたら,どのようなbehaviorを企業がとるか考えてみよう。在庫不能ということは,売れ残りは全て損失になるということだから,まず売れ残りを極小にすること,そして売れるときには最大限高く売ることが合理的である。そのためには過大となる恐れのある設備を持たず,投資はできるだけ少なくする方が良い。もちろん発電にはある程度の規模の経済性はあるから,ある程度の規模は必要である。しかしこの規模は需要にマッチしうる最小限のものとなるだろう。言い換えれば予備の設備を持つ自発的なインセンティブは働かない。そして需要に対して供給が不足気味の状態にしておくほど高い価格で電力商品を売ることができる。
一般の産業では商品は在庫できるし,売れ残りの商品を適切にディスカウントして売ることができる。また,製造業と流通業は両立していて,流通部門で卸が商品を在庫して利益を上げることもできる。
しかし電力では市場に当たるものが電場しかないから卸業者は介在する余地がない。電力システム改革後は電力取引に卸市場という制度が新設された。この「卸」市場が円滑に機能するには,発電業者が需要に見合う発電量を買手に対して必要十分に供給していなければならな【238頁】 い。では発電事業者にどんなタイミングでも需要に応じた供給が可能なような設備形成が行われるだろうか。発電市場が競争的であればそのような投資インセンティブは働きようがない。利潤動機に従っている限り,供給は不足気味にしておくことが合理的だからである。つまり卸電力市場さらには受給調整市場・容量市場などという仮想的な流通市場を構想することが定常的な電流を確保するという社会的目的とは整合しない。最近問題となる需給逼迫は臨時的に起こるものではなく,常時その恐れはあるのがこの仮想的流通市場の特性である。卸市場での価格の乱高下が投資のインセンティブを与えるという考えもあるが,電力市場全体の不確実性は高く,一時的な価格上昇が投資を促進することはありえないだろう。この点で発電所の建設はある規模以上の大きさのものなら数年以上の建設期間が必要だということを考慮せねばならない。将来の高価格が続くという予想がなければ,発電所投資は起こらない。
図−7の説明では発電部門は物理学的に見ると市場における競争が可能だとしたが,実は発電される電気という商品つまり電場を作る近接作用を供給するというビジネスは,送配電の持つ特性と不可分の関係にある。現実に発電市場という市場自体は十分に成立しているが,そのときは保存できない電気という商品の安定的な買い取りの仕組みが同時に存在しているのである。米国のPJMが典型例である5)。PJMは買手を含む電力事業者の一種のカルテル組織であり,PJMの決定は強制力を持っている。
日本の電力システム改革は地域独占という垂直統合システムを革新するという意欲的な取り組みである。しかし電力システムはこれまで論じてきたように,垂直統合されている物理的な合理性があった。独占は大きな社会的弊害を伴ったが,それを単に「アンバンドル」するというアプローチは,物理的に見て果たして合理性があるのかを十分に検討する必要があった。現在次々と生み出されて来ている,卸市場・需給調整市場・容量市場というようなアイディアは,安定的に電力を供給するという目的に合致するのか言い換えれば定常電流の確保,静電ポテンシャルの保存という電磁気学的要請と電力会社の設備投資行動とが整合するのかが,不問に付されていたのではないかという懸念がある。
電磁気学の特徴は電子が粒子という3次元の物質であって物理的には剛体という観点から分析せねばならないことである。力学では質量mは点として扱われているので2次元で記述できるが,電磁気学で電子は粒子であり,その挙動が3次元の分析の対象となる。その上電子は電位差があると波として行動するという不思議な性格を持つ。したがって電子はそれ自身「主役」なのであり,「電磁気学が力学と異なる自然記述の方法なのである」(砂川[2018]p.12)。
これまで分析では電場という概念に焦点を当て,電荷と電気力線を説明した。しかしそれは【239頁】 電磁気学からすれば半面でしかない。前述したコイルに磁石が干渉するとコイルはそれに抵抗するように磁場を生み出すために電流が流れて電場が生まれるという現象が起きる。ところが逆に電場が生まれると今度は磁場が生まれるという現象がある。これはsequentialに生起する現象で電磁波と呼ばれる。この一連の現象は経済の交換プロセスと次のように対応すると見られる。市場取引では「もの」の流れと「資金」の流れは表裏をなしている。言い換えれば「もの」の授受があるときは決済がこれを裏打ちしている。
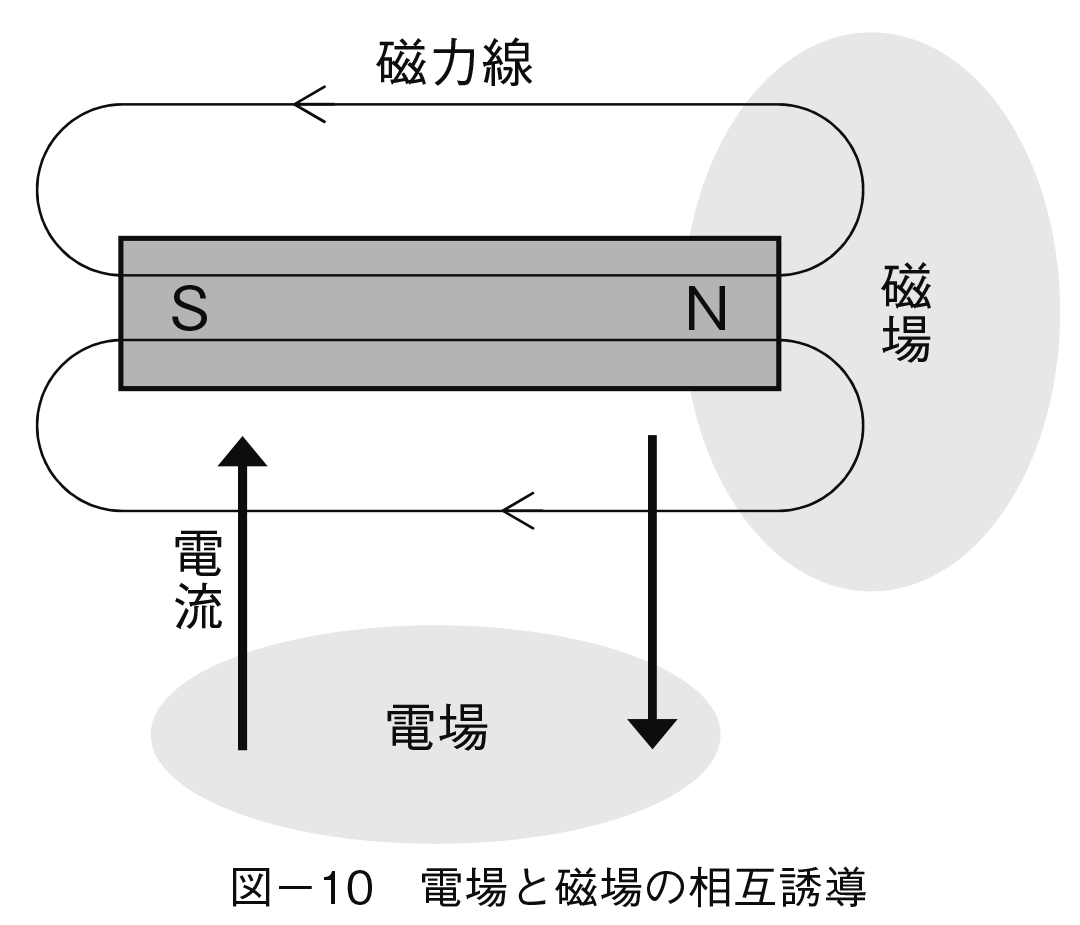
電磁気学では粒子が電荷を持っていて,そこから電気力線が出るとしたが,これを電気力線の「湧き出し」と呼ぶ。一方磁気はN極とS極とがあって発生する磁力線はNからSへ「吸い込まれる」。電気力線の電荷が湧き出すという能動的な活動(charge)に対して磁力線は逆に吸い込まれるのである。このような電場と磁場の関係は図−9で示してある。これはあくまでイメージ図にすぎないが,経済モデルで「もの」と「資金」の流れは連動して起こり,「資金」が流れるとその次に「もの」の取引が生まれ,また「金」が流れるというシークエンスと対応していると見ることができるのではないか。つまり電子のレベルで電子が取引の主体と見做されるのに対し,磁気は「資金」に相当する役割を果たしているのではないか(実際磁気は磁荷が存在しないとされているが,貨幣は決済の手段でしかないというのと対応している)。
物理学の法則は経済学のように公理系を設定して定理を導き,実証分析で統計的有意性を見るというところから生まれるものではない。物理学ではまず繰り返される実験の結果,観察された事実が履がえしようがないと受け取られた後,それを説明する論理的モデルが提出され,アクセプトされたもののみが残っている。次に紹介するマクスウェル方程式もそのような歴史的経緯を経て確立されたものであり,(1)から(4)はパッチワークと呼べるものである。
ここでマクスウェルの4本の方程式を参考までに紹介する。表記について変数はすべてベクトルで表されていること,∇(ナブラ)は演算子で3変数で偏微分するときの手順を示すものである。
【240頁】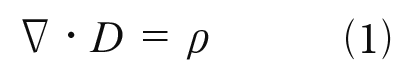
これは電荷が与えられると電気力線が何本も出てゆくという図−3の状況を示したものである。Dは電束密度と呼ばれるもので電荷から伸びている電気力線の密度,ρは電気力線の本線である。つまりどのくらい活発に電子が湧き出すかを表している。
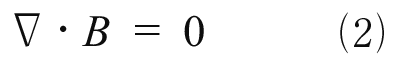
Bは磁場に相当し,磁場では磁力線はNからSへ吸い込まれて一本も出ていかないという状況つまり図−10の上の部分に相当する。
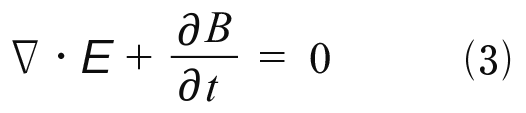
Eは電場,Bは磁場だから両者は磁場が動くとそれに抵抗するように電場が誘導される(起電力が生じる)ことを示している。一般にファラデーの電磁誘導の法則と呼ばれているものである。このメカニズムによって発電機で自由電子が生まれることはすでに説明した。
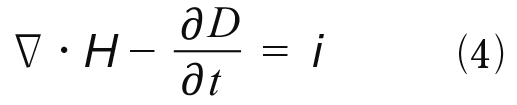
(4)は(3)の双対的な関係で電場Dが動くと磁場Hを生むような電流i(変位電流)が生まれることを示すものである。そのイメージは図−10で描かれている。これをアンペール・マクスウェルの法則と呼ぶ。
以上がマクスウェルの方程式と呼ばれている方程式群であり,本稿で解説した電子の挙動の諸側面を表現したものである。これらはすべて実験結果を積み上げ,それを理論化したものであって,経済学の一般均衡で登場するような連立方程式ではない。(1)から(4)が解を持つにはいくつもの端点の諸条件を必要とする6)。
砂川重信 (2018)「電磁気学」(岩波書店)
――― (2017)「電磁気学の考え方」(岩波書店)
田原真人 (2011)「電磁気学がわかる」(技術評論社)
南部鶴彦 (2017)「エネジーエコノミクス第2版」(日本評論社)
――― (2020)公益事業研究第72巻第1号「電磁気学と経済分析の接合の試み」