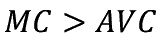�����W���o���������i�m�������������j�ɂ��ݔ������s���̕��́F
Uzawa-Penrose ���ʂ̍ĕ]��
�암�@�ߕF
�ݔ������s����s�m�����Ǝ�ϊm���Ƃ������_���瑨����Ƃ����A�v���[�`�̓P�C���Y�E�����[�C�ȗ��̓`���ł���B���������̃A�v���[�`�͂�����V�ÓT�h�̓������_�̘g�g�ł͏������Ă��܂��Ă��邱�Ƃ�I�m�Ɏw�E�����̂�Uzawa�m1969�n�ł������B�F�f���́C�ݔ������Ƃ͒P���ɓ��������𓊉����邱�ƂŏI��炸�C��Ɠ��g�D���ĕ҂��L�@�I�ɑg�ݒ����Ƃ����y�����[�Y�^�̊�Ɛ����̎��_���s���ł��邱�Ƃ����f���ɖ����I�ɓ��������B��������������ɂ͐V�K�̃A�C�f�B�A�ł��邪�̂ɒ��ʂ��鏔�X�̖��C���������đO�i���邽�߂̒lj��������K�v�Ȃ̂ł���B��q���郂�f������肵�ē��˂ł͂��邪�C�F�f����{�_���̊ϓ_����v��C�����ɂ���Ċ�Ƃ��B������͂��̊�ƋK�͂� V �Ƃ���ƁC V �͏������� I �ƒlj����� F �Ƃɂ���ĒB������C
V �� I �{ F
�ƕ\�������B
Dixit-Pindyck�m1994�n�́C���Z�I�v�V�����ɂ�����Black-Scholes�m1973�n�CRobert Merton�m1973�n���m�������I�v�V�����l�̌����@�������ireal�j�����ɉ��p���āu�s�m�������̓����v�Ƃ����^�C�g���̉��Ɋm���ߒ������邱�Ƃ����݂��B�����ł͕s�m�����iuncertainty�j���u���E���^���ƈɓ��ߒ��Ƃ������w�I���u�ɂ���ĕ\������Ă͂������ɂ߂Ďc�O�Ȃ��ƂɎ����̐��E��`�ʂ���̂ɋ��Z�I�v�V�����̗��_�I���u�����̂܂܃R�s�[���Ă��܂��Ƃ����P�����Ɋׂ����B�܂����������̂̐ݔ��������f���������̕ϓ����f���ƑΉ�������Ƃ����菇�ɂ���ĕs�m�������̎��������ƌ����Ƃ����̂ł���B�u�s�m�����v�𓊎����f���ɓ����I�ɓ�������ɂ́C�P�Ƀ{���e�B���e�B�Ƃ�������lj����邾���ł͓����s���̐����ɂ͂Ȃ�Ȃ��B���̐������ƊO���I�ɕs�m�����Ƃ�������lj����邾���ŁC������̂��s�m�����ɂǂ��Ώ����Ă��邩�̓��f�����ŋL�q����Ȃ�����ł���B���̌��ʁC��q����悤�ɃI�v�V���������zF�iDixit-Pindyck�mDXP�ȉ��ł͂��������n�̕\�L�@�ɂ��j�̎��o�ϓI�܈ӂ͖{���̎��ׂ��������ʂ����Ȃ����ƂɂȂ����B���̂Ȃ���Z�I�v�V�����Ƃ͋��Z�h�����i�Ƃ������Z�s��Ŕ�������錠���؏��̎���̕��͂ł���C�u�y�[�p�[�v�x�[�X�܂�_�Ƃ��Ă������݂��Ȃ��u�����v�C��ΏۂƂ���V�X�e���̌o�ϕ��͂ł���B��������A���̎��Y�܂�u���ʁv�������q�̂悤�ȑ��݂̋������ݔ������s�����ɂ͓K�p�ł��Ȃ�����ł���B��q���鐔�w�I���f���̊O�����炷��Ɨ��҂͌��ʂƂ��č����������̂ɂȂ�B���������f���̎��o�ϓI�܈ӂ͑傫���قȂ邱�Ƃ��������B
�Q�D�����_���E�E�H�[�N �����i�q�_��̓��_�̋���
�����_���E�E�H�[�N�̓E�B�[�i�[�iNorbert Wiener�j�m1923�n�ɂ���Ē��ꂽ�m���ߒ��ŁC����Ȍ�̊m���ߒ����f���̏o���_�ƂȂ��Ă���B����̎��o�ϓI�Ӗ�����q����u���E���^���Ƃ͓Ɨ��ɋ�ʂ��ė������Ă������Ƃ��d�v�ŁC�����ӂ�ƌo�ϕ��͂ɂƂ��đ傫�ȁu�T���v�̂��ƂɂȂ邱�Ƃɒ��ӂ��˂Ȃ�Ȃ��B
�܂������_���E�E�H�[�N��T�^�I�Ȑ��w�̐ݖ�Ƃ��Đ������悤�i�{���E�����m1978�n�j�B���܉��}�̂悤�Ȋi�q�_�������ē��_���i�q�_������R�Ɉړ��ł���Ƃ���B���͂��铮�_�� P �����_ Q �܂ňړ�����Ƃ� n ���œ��B����m�������߂邱�Ƃł���B�i�q�_�̂P�����P���Ƃ��C���_�͊e�i�q�_��łǂ̕������������̊m����1/4�Ƃ���B�܂�ǂ̕������Ƃ邩�͕s��ł���Ƃ����Ӗ��̃����_���l�X�����̕��s�̏����ƂȂ��Ă���B
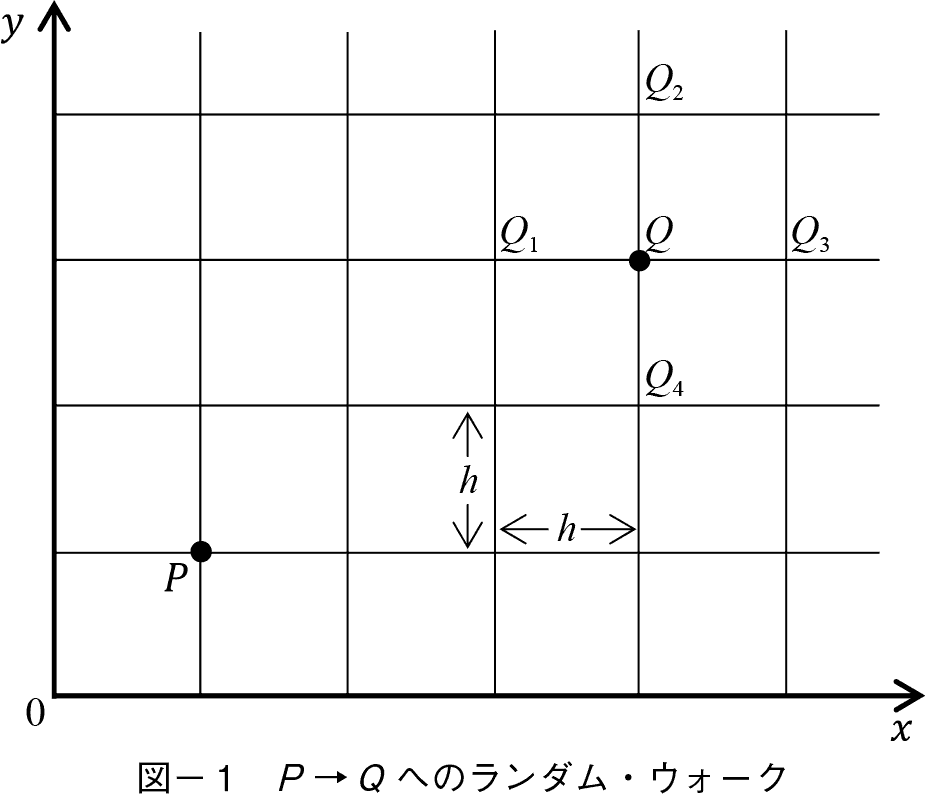
�����_�͎��O�Ɍ��܂��Ă��āC���_���P�����z����̂ɕK�v�Ȏ��Ԃ��сi���������đ��x��1/�сj�Ƃ���B�܂� n ���œ��B����ɂ� n �ю��Ԃ��K�v�ƂȂ�B����ɏ����Ƃ��ē��_�̓�������͈͂͐}��x����y�����Ɍ��肳��Ă���B���_�͂��̕ǂɂԂ���Ə�������Ƃ��������u���B
�_ Q �� n ���œ��B����m���� U �i P | Q , n �сj�Ə������Ƃɂ���B����Ƃ�������߂�ɂ́C Q �������O�� Q 1���� Q 4�ɒ��ڂ���Ηǂ�1�j�B
�Ⴆ�i n −1�j�ю��Ԃ� Q 1�ɓ�������m���� U �i P | Q ,�i n −1�j�сj�������� Q 1�� Q �֒H�蒅���m����1/4�ł���B����͑��� Q 2���� Q 4�܂ł̂ǂ̓_���Ƃ��Ă��������Ƃ�����C U �i P | Q , n �сj�y97�Łz �� Q 1���� Q 4�܂ł̊��Ғl�Ŏ��̂悤�ɕ\���ł���B
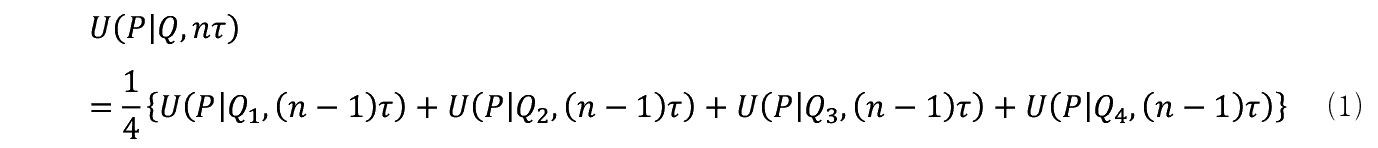
���w�I�Ȗ��͒�_ Q �ɓ��B����m������������ǂ̂悤�ɋ��߂邩�ł���B�����������Ő��w�𗣂�ē��_�̍s�����l���Ă݂悤�B�����_���E�E�H�[�N�͐����Ƃ���āC�������t���t�����Ȃ�����䂪�ƂɒH�蒅���v���Z�X�Ƃ��`�e�����B���̕\���ŏd�v�Ȃ̂͐����ɂ͊i�q�_���ړ����邾���̃G�l���M�[�����邱�Ƃ�O��Ƃ��C���̃G�l���M�[�̌��ɃA���R�[������������Ƃ����_�ł���B�܂�P/�тƂ������x�� n �̊i�q�_���߂�����������́u�́v���Öق̂����ɑO��ƂȂ��Ă���B����ɐ����͉��̉ƂɒH�蒅����̂������̊m���̓[����������Ȃ��̂Ʉ��Ƃ����^�₪����B����͑��ɂ͐����Ă��Ă��A�蓹�͉����Ă���Ƃ���������邪�C�o�ϓI�Ɍ���A���Ƃ������Ƃ́greward�h���邢�͕։v�� n ���̃G�l���M�[���g�킹�Ă���ƍl������B�܂� Q �_�ɒH�蒅�����̊m���ɂ͂P�Ƃ���reward���\�߉��肳��Ă���ƍl���邱�Ƃ��ł���B���̂悤�ɍl����ΐ������A��ē���m���Ƃ͌��E���p�ł���C���ꂪ n �ю��Ԃ��邢�� t ���Ԃ��g���Ƃ������E��p�Ɠ������Ȃ���Ȃ�Ȃ��Ƃ����������w�I�ɂ������Ȃ���Ȃ�Ȃ��B
�����Ŋm�� U �i P | Q , n �сj�����߂鐔�w�I�Ȏ葱�����l����B�܂����ԃт�����⑴���� U �i P | Q , n −1�j�������Ǝ���������B
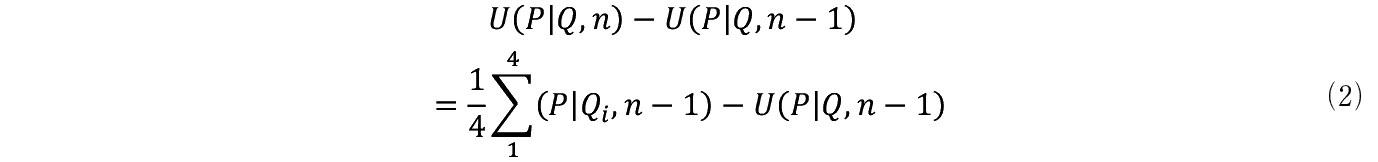
���������_�͎��ԁi n −1�j�т������� Q 1���� Q 4�܂łɗ��Ă���B
�� Q �_�ɂ�����i�q�_�̍��W���i x , y �j�Ƃ��悤�B
����� Q 1���� Q 4�܂ł̍��W�͊i�q�̕��� h �Ƃ���
�@�@�@�@�@Q1 : x − h , y
�@�@�@�@�@Q2 : x , y �{ h
�@�@�@�@�@Q3 : x �{ h , y
�@�@�@�@�@Q4 : x , y − h
�̂悤�ɕ\�L�ł���B����������⑵�͎��̂悤�ɕ\�����B
������ x �{ h �C x − h �̃O���[�v�� y �{ h �C y − h �̃O���[�v�ɕ����ď������Ƃ��킩��₷���B
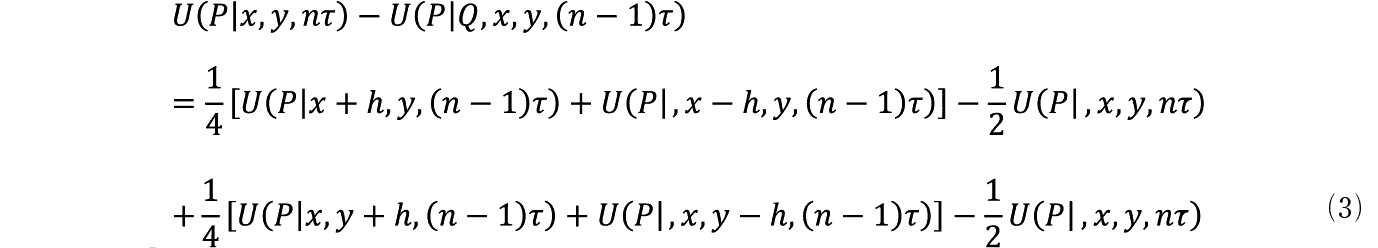
⑶�͈ꌩ�ώG�Ȏ��̂悤�Ɍ����邪�C��Q�s�ڂƑ�R�s�ڂƂ͗��U�^�ŕ\�������Q�K�Δ����y98�Łz �ɋߎ��I�ɓ��������Ƃɒ��ӂ���B
���Ȃ킿�������ߎ��I�ɐ��藧�B
�Ⴆ�� y �ɂ��� U �̂Q�K�̕Δ����W�� 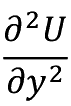 ��
��
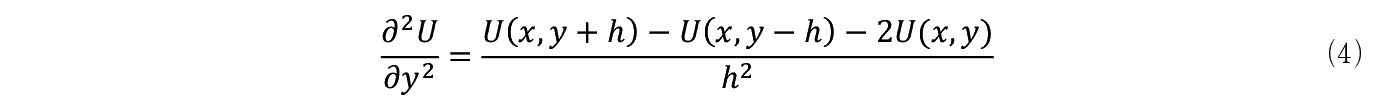
⑶���ɂ��Č���ƍ��ӂ� U �̃ѕ����������ł���C�E�ӂ� x ����� y �ɂ��Ă� h 2 �����̍����ƂȂ��Ă���B
���܃тɂ���
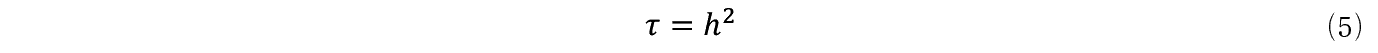
�Ɖ��肷��B
�ȏ�̏����̉��ɍ��ӂ��тŁC�E�ӂ� h 2 �Ŋ��邱�Ƃ��ł���B�����ăт���� h �������ȂƂ�⑶����
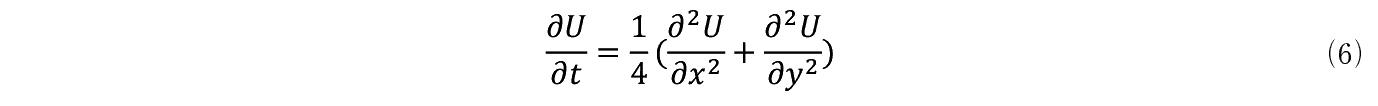
�ƕ\�����Ƃ��ł���B
���ӂ͖ڕW�n�_ Q �ɓ�������Ƃ��̌��E�m���ł���C�E�ӂ͊i�q�_��� x ������ y �����Ƀ����_���Ɉړ�����Ƃ��̌��E�m���ł���B�ړI�n�ɓ��B����Ƃ���reward���P�Ȃ̂ō��ӂ͊i�q�_���g���x�����邱�Ƃ̌��E���v�C�E�ӂ� n ��i�q�_��ʉ߂��邱�Ƃɑ��Ďx�����G�l���M�[�R�X�g�i�܂����J�����[���j�̌��E��p�ł���C����炪�o�ϓI�ɓ������Ƃ������Ƃ�⑹�͈Ӗ����Ă���B⑹��1/4�͊��Ғl�����Ƃ��̊m���Ƃ���Ă��邪�C�{���͂��d�v�ȈӖ��������Ă���B����Fokker-Planck�������i�ȉ��ł�FP�j�ł͕��U���������̌W��D�͔M�G�l���M�[����������������B
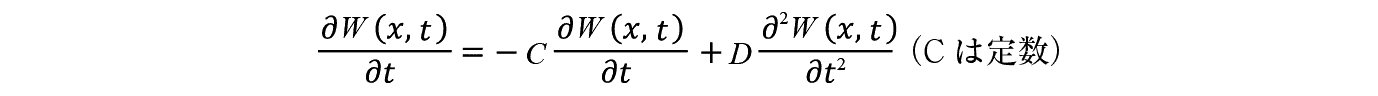
W �͓��_�����_ t �ɋ����� x �ł���m���ł���B�����ł� x �����݂̂̈ړ������肵�Ă���̂ŁC x ����Q�����ւ̈ړ�������⑹��
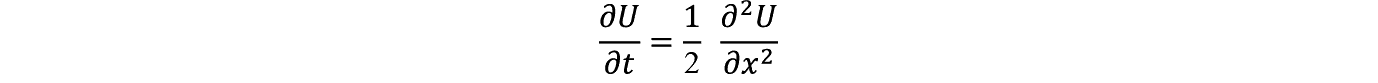
�ƂȂ�BFP�̌W�� D �͂����ł�1/2�ɑΉ����Ă���B
�������C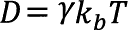 �ł���B������
�ł���B������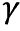 �͖��C�W���Ck B �̓{���c�}���萔�C����� T �͐�Ή��x�ŁC D �͔M�G�l���M�[�ł���B
�͖��C�W���Ck B �̓{���c�}���萔�C����� T �͐�Ή��x�ŁC D �͔M�G�l���M�[�ł���B
D �͌�o����⒅���狗�� x �Ǝ��̊W������B

���������ă����_���E�E�H�[�N�̌W���Ƃ̊Ԃɂ�
�y99�Łz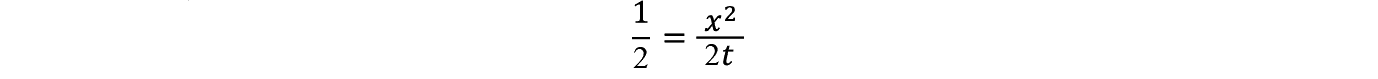
����� x 2 �� h 2 �Ə���������
�@�@�@�@ t �� x 2 �� h 2
����āC t ���тł���� D ��1/2�̑Ή������藧�B
����͐}−�P��
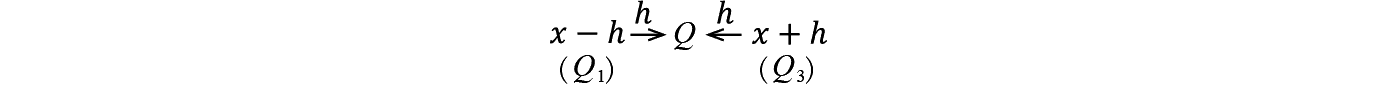
Q 1�C Q 3���炠�ƈ���� Q �ɒH�蒅���Ƃ������Ƃ��Ӗ����Ă���B���Ȃ킿1/2�Ƃ����W����D�Ƃ����M�G�l���M�[�ɑΉ����Ă���̂ł���B
�����Ŏ��̂��Ƃɒ��ӂ��悤�B Q i���� Q �܂ł̊i�q�_�P���̋����� h �Ƃ���B����ƂP���̊i�q�_��ʉ߂���̂ɕK�v�Ȏ��� t �͑��x��1/�т�����
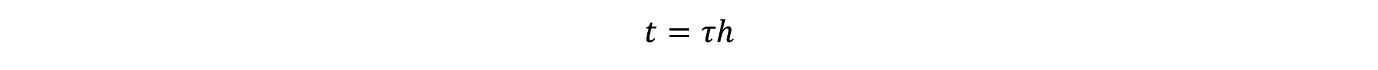
�ƂȂ�B������t�ƃт̔����ω����ɂ���
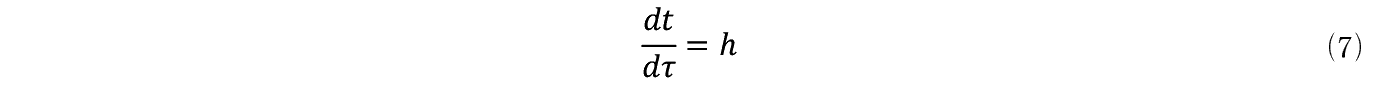
�����藧�B
����ɔ�����t�ƃт̊Ԃł�
���邢�́@�@�@�@�@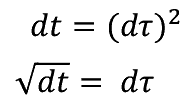 �@�@�@�@�@⑻
�@�@�@�@�@⑻
�ƕ\�����邱�Ƃ��ł���B���̊W����q����u���E���^�����ɓ��ߒ��Ƃ��ĉ��߂���Ƃ��d�v�Ȗ������ʂ����B
�R�D�����_���E�E�H�[�N�ɐ��ޏ�����
�����œ��������E�B�[�i�[�ߒ��ł͍X�ɖ�������Ă��Ȃ��Öق̉��肪����������B
�܂����ɂ́C�ڕW�ƂȂ� Q �_�́i x , y �j���ʏ�̔C�ӂ̓_�ł���C�����֓�������̂� n ���i�q�_���ړ�����Ƃ����ݒ�� n �Ƃ��������̓��f����������ł̔C�ӂ̒l���Ɖ��肳��Ă���2�j�B�����ŕ��s�҂� P ���� Q �܂ōŏ��̕����ŕ����Ƃ����ӂ��ɖ���ς��Ă݂悤�B�����⑺�̍��ӂ� n ���ł���ȏ�m�������������邱�Ƃ��ł��Ȃ��i���������K�v���Ȃ��j�Ƃ��������ɂȂ�̂���U / ��t��0�łȂ���Ȃ�Ȃ��B����������
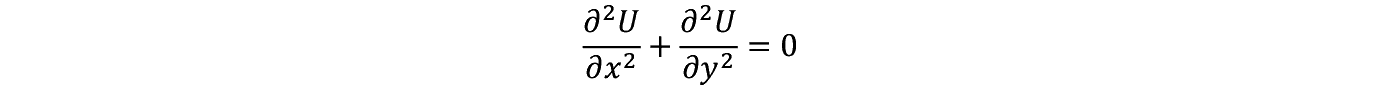
����͕����w�Œ���Ԃ��������v���X�������ƌĂ�钲�a���̂P�ł���B�܂蕨���w�ƌo�ϓI�ɍ����I�ȍs���Ƃ̖��m�ȑΉ������邱�Ƃ��ł���B
���ɂ͓��_�̍s��������Â�����̂Ƃ��āC����i�q�_�ɗ��Ƃ��C�l�������Ăǂ̕����֓����̂��̊m����1/4���Ƃ��Ă���_������B�܂肱�̓��_�͋ɂ߂č����I�Łi x , y �j���ʏ�̉\�����ɔ��f���Ă��邱�ƂɂȂ�B�����_���ȍs���Ƃ����Ӗ��͒lj��̏�Ȃ������ɗ�Âɂ�����\���ɓ����̃E�F�C�g��^����Ƃ������Ƃ��Ӗ����C���_�͍����I�Ȕ��f��̂Ɖ��肵�Ă���̂ɓ������B�����_���l�X�́u�h�炬�v�Ƃ������t�ɒu���������邪���茩�Ƃ����Ӗ��ł͂Ȃ����Ƃɒ��ӂ��˂Ȃ�Ȃ��B
��O�ɂ́C���_�� P ���� Q �܂ňړ����邱�Ƃ�O��Ƃ��āC Q �ւ̓����m�������߂�ꂽ���C Q �_�ł�reward 1������Ƃ��������ŁC���̂悤�Ȉڍs���K�R�I�ƌ����邩�Ƃ������ł���B���ʂƂ���⑹���͌o�ϓI�ȋύt�_�ł��邪�C�E�B�[�i�[�ߒ��ɂ͓��_�������܂Ō�������͖͂����I�ɂ͑��݂��Ȃ��B��q�����悤�ɐ����ɂ͋A���{�\������Ƃ��������͜��ӓI�ł���B���������ăE�B�[�i�[�ߒ��ł̋ύt�_��ۏႷ��ɂ͓��_�̓����͈͂Ɂu�ǁv�����邱�ƁC�����Ă�������ֈ�����́C�܂蒣�͂Ƃ������̂������Ƃ��������lj�����K�v���o�ϓI�ɂ͏o�Ă���B
��l�ɂ́C���_�͊i�q�_������̒�R�����X���[�Y�Ɉړ����邱�Ƃ��Öق̑O��ƂȂ��Ă���B�܂蕨���w�I�Ȗ��C�͂������ł͓����Ȃ����Ƃ����肳��Ă���B��������Γ��_�ɂ͑傫�����Ȃ��̂łǂ̕��ʏ�ł����C���Ȃ��Ƃ������Ƃ����Ȃ���Ȃ�Ȃ��B����Ɠ��l�ł��邪���_�ɑ傫�����Ȃ�����̓����ɂ���āi x , y �j���ʂ��������Ƃ͂Ȃ��C�X���[�Y�ȕ��ʂ���ɗp�ӂ���Ă��邱�Ƃ͓��R�ł���B
DXP �mp.65�n�ł̓u���E���^�������̂悤�ɂ��ē�������Ă���B
�u���E���^���Ƃ̓E�B�[�i�[�ߒ�����ʉ��������̂œT�^�I�ɂ͎��̂悤�ɏ�����B
�y101�Łz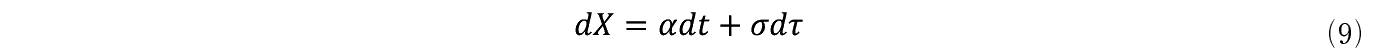
������ X �̓u���E���^�����闱�q�̈ړ������C�E�ӂ̃��̓h���t�g�E�p�����[�^�ŁC�܂���Ғl�ɑΉ����C��Q���Ђ͑O�q���������_���E�E�H�[�N���闱�q�̃����_���ȓ����i�܂�W�����̕����j�ł���B���̂悤�Ȍ`�Ńu���E���^�����Љ�ꂽ��ɂ́C�u���E���^�����ɓ��ߒ��ɂ�菑�������ċ��Z�I�v�V�����ɂ�����I�v�V�����l�̌v�Z�Ɠ����菇�ŃI�v�V�����l�����߂邽�߂̕��͂��i�߂���B�������{�����ƃЂ̓u���E���^�������̂̓�����\��������̂łȂ��Ă͂Ȃ�Ȃ��B���ƃЂƂ͉��Ȃ̂��̐������K�v�Ȃ̂���DXP�ł�entrepreneur�i�N�ƉƁj����l���ƂȂ镨���w�Ƃ��Ẵu���E���^���̃��J�j�Y���͈�ؐG����Ă��Ȃ��BDXP�̕��͂̎葱�������������̌o�ϕ��͂�ڎw���ɂ��S�炸�C���A���E�I�v�V�����̃��f�������Z�I�v�V�����̃��f���ɊҌ�����Ă��܂��C���A���E�I�v�V�������ݔ������s���̕��͂Ƃ͂Ȃ��Ă��Ȃ��B�܂�DXP�̕��͂ł͋��Z�����̃y�[�p�[�E�x�[�X�̌����̔������f���Ǝ����̐ݔ��x�[�X�̎��{�`�����f�����S����ʂ����Ȃ����ƂɂȂ��Ă��܂��̂ł���B
�O�߂ɂ����铮�_�̈ړ����f���ƃu���E���^���ɓo�ꂷ������q�Ƃ̍��{�I�ȍ��ق́C���_���傫���������Ȃ���������̓_�ł���̂ɑ��C�u���E���^���̗��q�͎��ʂ����u���́v�̐��i�����Ƃ������Ƃł���B���Ȃ킿���̂͂R������K�v�Ƃ��C���i�^�����s����̂ł���B�u���E���^���ł͗��q���ړ����悤�Ƃ���Β�R����̂͂��̂��߂ł���B��������_���E�E�H�[�N�̓��_�ɂ͑傫�����Ȃ��̂Œ�R���邱�Ƃ͌������݂��Ȃ��B���Z�I�v�V�����œo�ꂷ�鏤�i�͌����؏��ł��邩��C�����I���Y�����̎ʑ��ɂ������C��R�̂Ȃ��i�q�_����ړ����铮�_�ɑΉ����Ă���B����u���E���^���̗��q����R���Ȃ�����i����v���Z�X�́C�V�K�̓����v���W�F�N�g�����͂̊����甽���E��R���C������������Ȃ���ΑO�i�ł��Ȃ��Ƃ����ɑΉ�����B�����Ē�R�i���C�j�͂��傫���ė��q�̉^������~����Ƃ��́C���͂��O������^���ď��߂Ĉړ��ł���Ƃ������l���Ȃ���Ȃ�Ȃ��B���̂悤�ȃu���E���^���ŗ��q�����ʂ����Uzawa�Ŏ��グ��ꂽ��Ɛ����̃v���Z�X�ł̓����̒�����p���f���ƑΉ����Ă��邱�Ƃ͖��炩�ł��낤�B�����ē�����̂��o������͂��̃u���E���^���Ƃ������I���J�j�Y�������f���������CDXP�̂悤�Ƀu���E���^����⑼���Ƃ��Ĉ������Ƃ͈ȏ�̘_�_���ʼn߂��邱�ƂɂȂ���B
�����Ŗ{�e�ł͂܂������w�I�ȃu���E���^���̖{������Ƃ��č]��m1973�n�Ɋ�Â��Đ�������B�����ău���E���^�����闱�q�̋��������f�����������̂Ƃ��Ĉ�ʓI�ɗ��p����Ă��郉���W���o���iLangevin�j�����������āC�ݔ������Ƃ̌��т����������B
�S−�P�@�����W���o���������ɂ��u���E���^���̃��f����
�u���E���^���Ƃ͎��m�̂悤�ɁC��������q���������̌n�̉��Ń����_���ɉ^������l�q�̂������̂ł���B���������Ď��グ��n���Ƃɗl�X�ȃo�[�W���������邪�C�����ł͐����ňړ���������q�Ƃ�����̓I�ɗ������₷���P�[�X�ōl�������i�ȉ��̋c�_�͋C�̂ɂ��Ă����l�ɐ��藧�j�B�����q�̑傫���͐����q�����傫���������ɂ��鐅���q�Ɏl����������Փ˂���Ă���Ƃ���B�����q�̓T�^�Ƃ��ăR���C�h���l���悤�B����͒ʏ�̂P�}�C�N�����[�g�����x�̂��̂��w�����厖�Ȃ̂͐����q�Ƃ̑��݊W�ł���B
���̗��q�͐}−�Q�̂悤�Ȍn�̒��ɂ��邪�����ɖv����̂ł͂Ȃ������ɕ����Ă���B�����y102�Łz �����Ă��ꂪ�������߂̏����Ƃ��āC����̔�d����'�Ƃ��C���̔�d���ςƂ���ƕ��͂̌�������
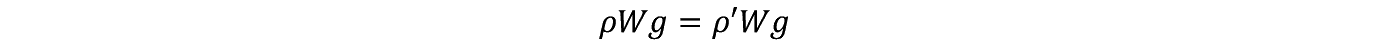
�i������ W �͕��̂̑̐ρC g �͏d�͉����x�ł���j
�����藧���Ȃ���Ȃ�Ȃ��B�܂��d�ɂ��Ă̏���
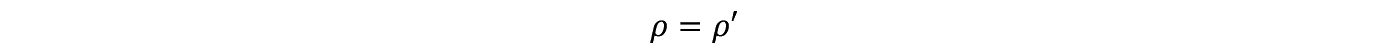
���K�v�ł���B
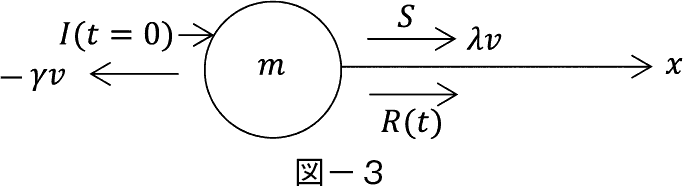
���q�͐����q�̎l����������̏Փ˂ɂ���ē˂���������Ă���B�����q�ŗ��q�̐^���ʂ���Փ˂�����̂͌����Ă��Ă���ȊO�͗��q����������Ƀv�b�V������ł��낤�B�u���E���^���̕��͂ł͗��q�̋O���� x ����݂̂ƒP��������B����ƕW���I�ȃ��f���ł͎��̂悤�ɉ������Ă���B
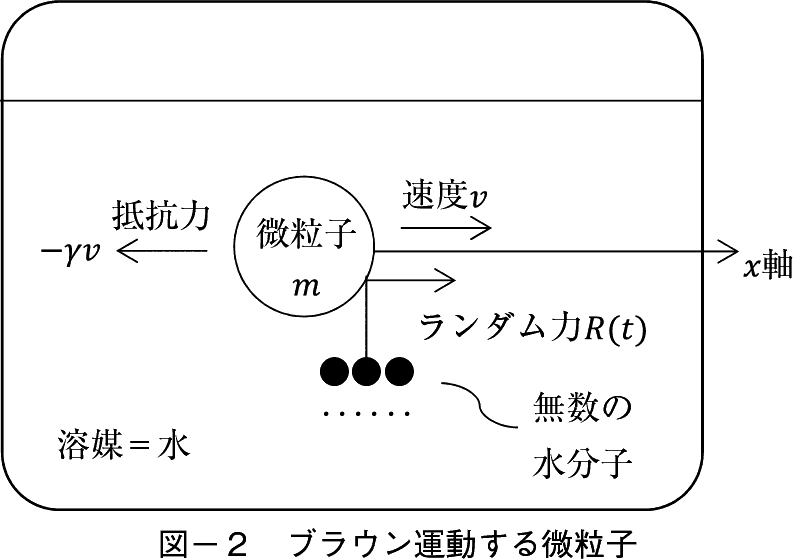
���q�͏����x v �i0�j������ x ������E�����Ɉړ�������̂Ƃ���B���̂Ƃ����q�͍��̂�����E�����֓������Ƃ���Ƃ������q�̒�R����B���������ʕ����ȊO�̐����q�͉E�����ւƗ��q�������o������������i�㉺�̗͂͑��E�����Ƃ���j�B���̐����q�̓����̓����_�������烉���_���ȗ́i�h���� R �i t �j�j�����q�̋��������E����B
����ɗ��q��������ł���e��ɂ͔M���������Ă���Ƃ��悤�B���̔M�̗͂Ő����q�̊����͊����ɂȂ�C���q�ɕ��i����͂�^����B����ŗ��q�̉E�����ւ̑O�i��j�ޗ͂�����C���̖��C�͂͗��q�̓������x�ɔ�Ⴗ��Ɖ��肵�C���萔�����Ƃ���B�����W���o���������Ƃ͗��q�̊��������̉^���������ŒP�����������̂ł���B�����ŗ��q�̓��������� X �i t �j�Ƃ����q�̎��ʂ� m �Ƃ���B�^����������
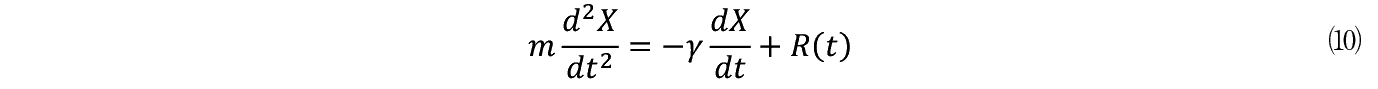
���ӂ� 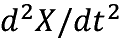 �͉����x�ł���C���C�͉͂E�����ւ̉^���Ƌt����������}�C�i�X�̕����C�����͂͗��q���E�����֓������͂�����v���X�̕�����t����B
�͉����x�ł���C���C�͉͂E�����ւ̉^���Ƌt����������}�C�i�X�̕����C�����͂͗��q���E�����֓������͂�����v���X�̕�����t����B
������
�y103�Łz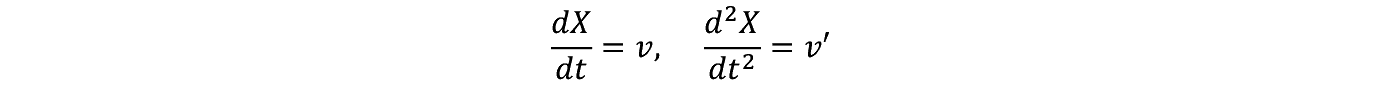
�Ƃ����⑽�͎��̂悤�ɏ�����B
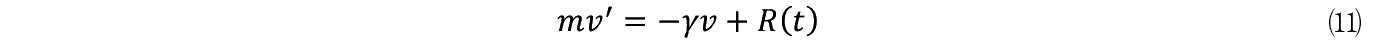
������ R �i t �j�́C�O�߂̃E�B�[�i�[�ߒ��Ŕ����q�������_���E�E�H�[�N������͂ł���B�����q�̈ړ������̓����_�������� R �i t �j�̊��Ғl������
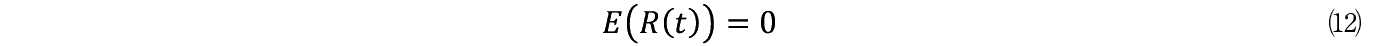
�����藧�B��������u���E���^����������q�i�R���C�h�j�ɍ�p���� R �i t �j�̓z���C�g�E�m�C�Y�Ƃ������i�������Ă���B������⑾�̊��Ғl���Ƃ�� R �i t �j��������
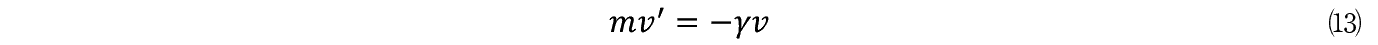
�����藧�B
����͒P���Ȕ����������ʼn���
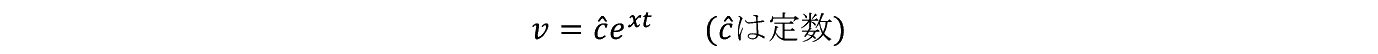
�ƂȂ�B
�����p����⒀���� x �����߂��
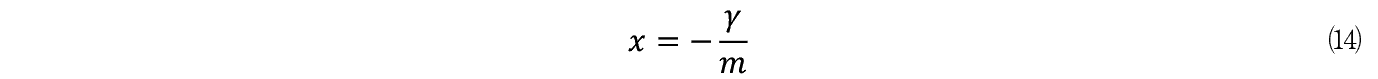
���Ȃ킿���߂鑬�x v ��
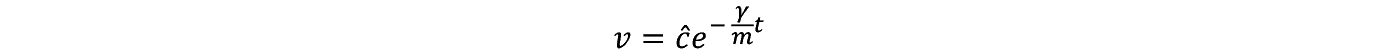
����� t ��0�ɂ����ĊO���̗͂�������� v �i0�j�Ƃ��������x���^������B���̊O���̗͂� I �ƌĂԂ��C����͌�ɐ�������B
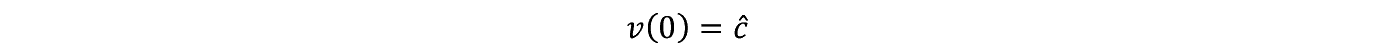
�ł��邩��
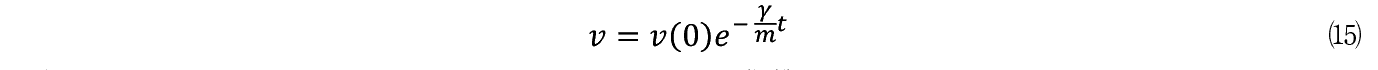
���Ă�����⒁�ŗ^������ x �̕����w�I�Ȓl�𐄒肷��B
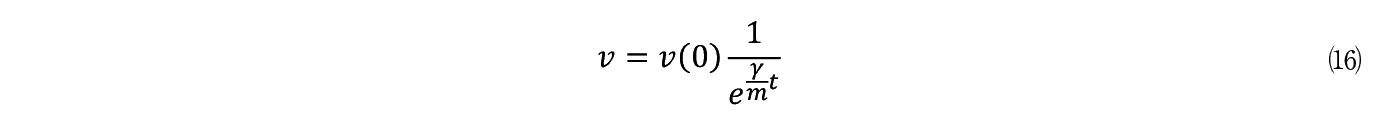
�����w�ł͊��K�I�Ƀ�/ m �̋t�� m /���ɒ��ڂ���B������ m /���̒l�͎��ۂɎ��̂悤�Ɍv�Z�ł���B�܂����q�̑傫�� m �͔��a�� a �Ƃ����
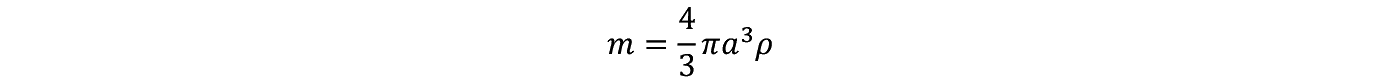
�ł��邪����͐��ɕ�����ł���̂Ő�q�����悤�ɐ��Ɠ�����d�������C�ρ�1�ł���B��������ŗ��q�����R�̓X�g�[�N�X�̖@���ɂ����
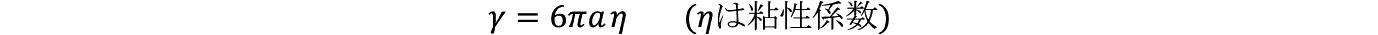
�ł��邱�Ƃ��킩���Ă���B����������
�y104�Łz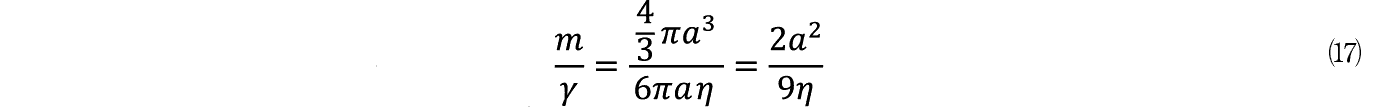
�R���C�h�̔��a a ��0.5�~10 −6 m �Ƃ��C���̔S���W����10 −3 Pa/sec�Ƃ����
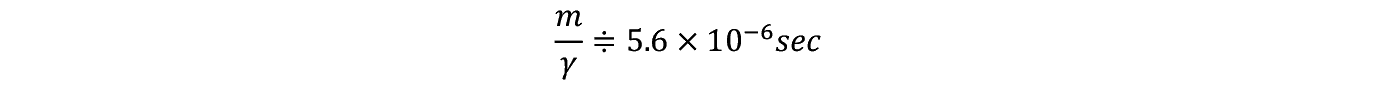
�Ɛ��v�����B���������Ă���̋t���ł���⒂�̃�/ m �̒l�͋ɒ[�ɑ傫�����瑬�x v �̓[���ŁC�����q�͐����̖��C��R�͂ɂ���ē����o���Ă��u���ɒ�~�������Ă��܂��B
���̌v�Z�v���Z�X�Ŗ��炩�ƂȂ�̂́C���� m �̎��ʂƐ��̒�R�̑��Δ䂪���q�̑��x�����肷�邱�Ƃł���B�����ł̃u���E���^���ł͔����q�͎���̑��x�őO�i���邱�Ƃ͂ł��Ȃ��B�������u���E���^���ł͉ԕ��̔����q���������l�q���ώ@�����B��/ m �ł͒�~���Ă��܂����q�����̉^�����邩�ƌ����� R �i t �j�Ƃ��������͂���������ł���B���ăA�C���X�^�C���m1905�n�́C�}�N���I�ȓ��v�͊w�̎�@��p���ė��q�������_���ȗ͂ɂ���Ĉړ�����Ɖ��肵�āC���̈ړ����������肷�郂�f�����l�����B�����Ĉړ������i�ʒu�j X �̂Q��̊��Ғl�������ƂȂ邱�Ƃ����B
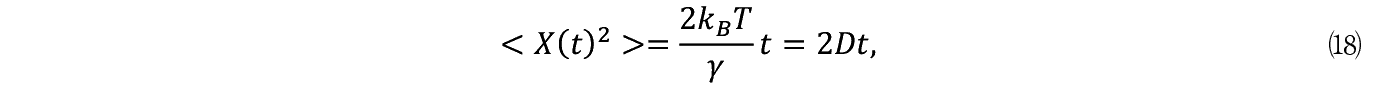
������< >�͊��Ғl�Ck B �̓{���c�}���萔�C T �͐�Ή��x�ł���B D �͌�ɓo�ꂷ��u��炬�v�ł���B����͓��ʏ����ȕ����w��̐��ʂł���C�����̖��Ƃ͊W�Ȃ��悤�Ɍ�����B��������q����悤�ɓ����̎�̂��u���E���^����������q�ɓ��e���čl����Ώd�v�ȈӖ��������Ƃ��킩��B
�S−�Q�@�m�������������̉�
���Ƀ����W���o��������⑽���邢��⑾�ɖ߂�C�m�������������Ƃ��Ẳ������߂悤�B⑽�ł̓����_���� R �i t �j�����݂��邱�Ƃɂ��C���x v �i t �j���m���ϐ��ƂȂ�B
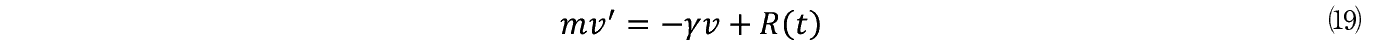
�܂� R �i t �j�̃����_���ȕω��Ƃ̓E�B�[�i�[�ߒ��̓��_�̂悤�Ȃ��̂����炻�̊��Ғl��
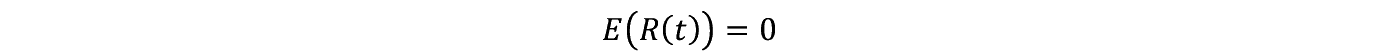
������ R �i t �j�� t �Ƃ������_�Ŗ����̐����q���Ԃ��荇���āC����n�܂��̓V�X�e���́u��炬�v�����o���Ă���B�u���E���^���ł́u��炬�v�͐��e��̒��̐����q�̏Փ˂����C���_��ς��ĎЉ���Ƃ������_���猩��ΗႦ����u�g�D�v���\�����Ă��鐬�����݂̏Փ˂������炷�Љ�́u��炬�v�ł���B���v�I�ɂ� R �i t �j�� t �ƕʎ��_�� t '�Ƃł݂͌��ɓƗ��ŁC����̎��_ t �ł̂� R �i t �j�̏Փ˂������炷�u��炬�v������B������ R �i t �j�̂����炷��炬�͂�炬�̑傫���� D �Ƃ��āC�f���^���͎��̂悤�ɏ�����B
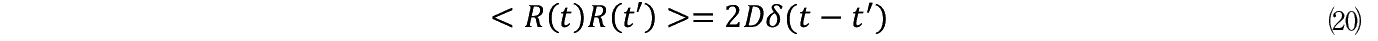
����� t �� t '�̂Ƃ��̓[���ŁC t �� t '�̂Ƃ��̂� D �Ƃ����傫���̂�炬�����B
���� R �i t �j�����݂��邽�߂�⑾���̗��q�̓u���E���^���Ƃ����O�Ղ�`���C�����W���o���������̑��x v �i t �j�̉�����A�C���X�^�C���̓�����⒅���Ƃ������ʂ�������B
D �����߂�ɂ͑��x���W���ƌĂ�鑬�x v �i t �j�̕��U
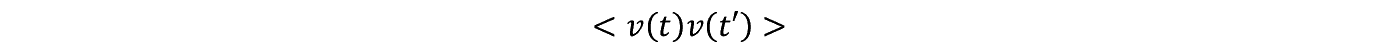 �y105�Łz
�y105�Łz
���v�Z����K�v������B v �i t �j��⒆�̔������������������ƂŎ��̂悤�ɕ\�����B
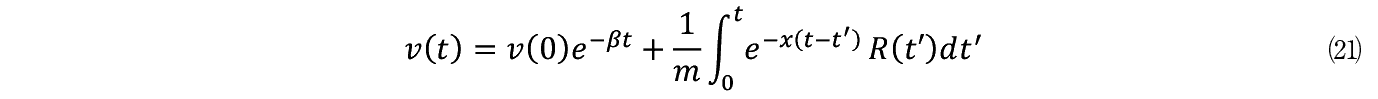
������ 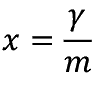 �ł���B
�ł���B
���x���W���� t �� t '�̂Ƃ�
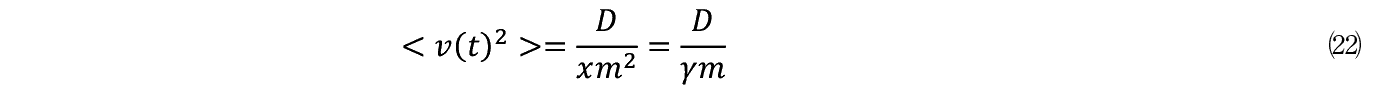
�Ƃ����\����B����ɃG�l���M�[�����z���𗘗p���� D �����߂邱�Ƃ��ł���3�j�B

�T�D�ݔ������s���Ƃ��Ẵ����W���o���������̉���
�����W���o���������ł͔����q�̉^���͒�R�̑��݂ɂ���ďu���ɒ�~���C�����_���ȓ����݂̂��c�邱�Ƃ��킩�����B���̏Ŕ����q�� x ����ɉ����Ĉړ������邽�߂ɂ́C�O�����珉���x v �i0�j��^���� I �ƒ��͂��Ȃ���Ȃ�Ȃ��B�����͂� S �Ƃ���Ɖ��}�̂悤�ɔ����q�ɂ� x �������� S �����̒��͂������B���� S ��
 �y106�Łz
�y106�Łz
��R�͂Ɠ��l�ɑ��x v �ɔ�Ⴕ�C���萔���ɂƉ��肷��C�V�����^���������͎��̂悤�ɂȂ�B
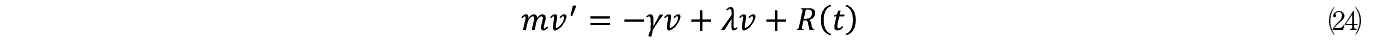
����̊��Ғl�����C������������������
�@�@�@�@�@�@�@�@�@�@�@�@
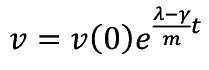 4�j
�@�@�@�@�@�@�@�@�@�@(25)
4�j
�@�@�@�@�@�@�@�@�@�@(25)
�����q�����i����ɂ�
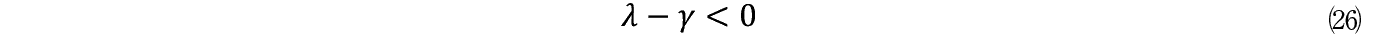
���K�v�ł���B
�ɂ̓������������ƍl����K�v������B�����ɂ�������Ȃ� m �̉����x v '�͐��ɂȂ邩�痱�q�͒�R�Ƃ��������ԂƂƂ��ɉ����I�ɔ�яo���Ă��܂����ƂɂȂ邩��ł���B
�ݔ������̊ϓ_���猩��C�v���W�F�N�g�ւ̒�R�����k��������悤�Ȏ�i���ɂł���B�ɂ����ʓI�Ȃ�Г��I��R�ɑR�ł��邪�C�����ɂ��������傫���ƂȂ�C�����v���W�F�N�g�͎Г��̒�R�������R�Ɋ����ł���B�܂��R�͂Ȃ��ɓ������B���������Ēlj����� F ���K�v�ƂȂ�P�[�X�̓ɂ��������������Ƃ��Ɍ��肷��B
�ɂ͂��̃v���W�F�N�g�̏�����������ł���悤�ȁC�v���W�F�N�g�̐V���^�C�~���O�̗ǂ��Ȃǂ��A�s�[������헪�I�s���ł���B
(25)�͏���������
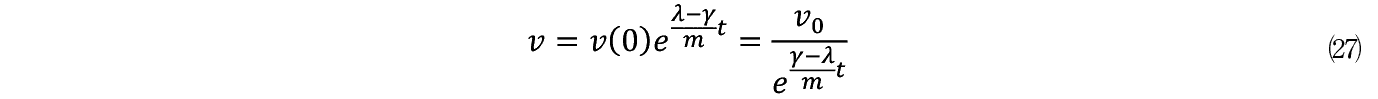
�����ɂ���������x�ȏ�傫���Ƃ��́C�Ƃ��鎞�_ t '��
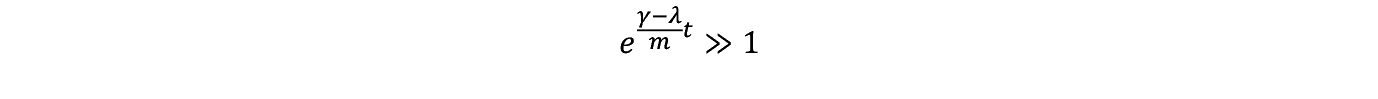
�ƂȂ�ł��낤�B�܂�ɂɂ���ď����̎��_�܂Ńv���W�F�N�g�͐��i�������邪 t '�Ő����͒�~����B�����Ă��̊ԓ����v���W�F�N�g�𐄐i������̂� R �i t �j�̎��h���͂ƂȂ�B
���Ĉȏ�̕��͂���m�������������̉��Ƃ��đ��x v �i t �j�ƈړ����� X �i t �j�Ƃ�B
���x v �͋��� X ������������̂����C�ړ����� X �͐ݔ������Ƃ��Č���ƌ��݂���鎑�Y V �̋K�͂�����ɂ����邩�� X �� V �Ƃ���
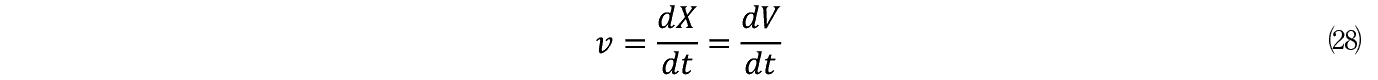
����������(25)�� V �ŏ�����
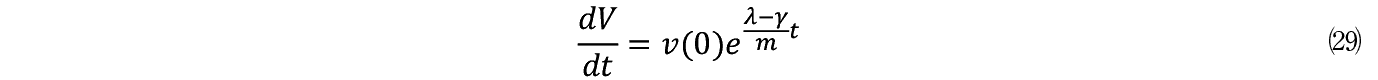
����� t �ɂ��Đϕ�����K�� V �����߂���B
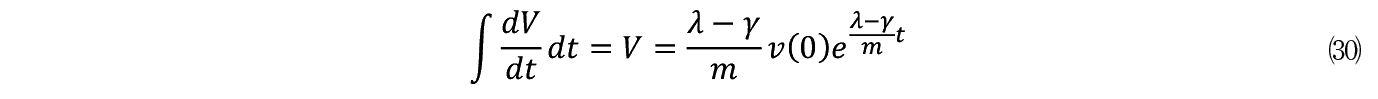 �y107�Łz
�y107�Łz
������������ V ��(29)�������
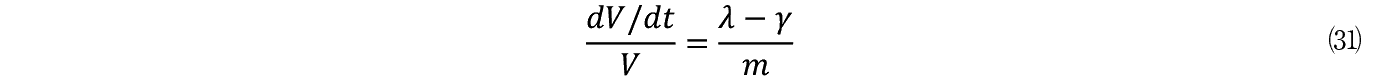
����Ď������藧�B
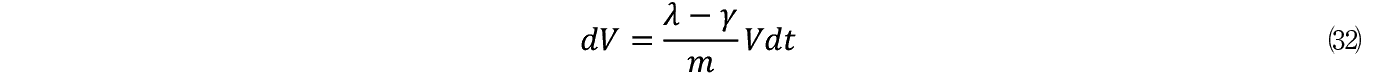
���̍�����ɏd�v�Ȗ������ʂ����B
�����(23)�𗘗p�����
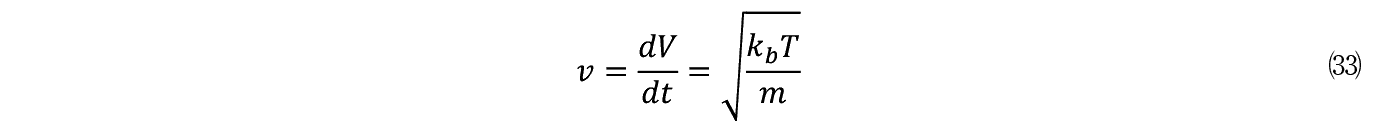
�����Ń����_���E�E�H�[�N�œ������ꂽ�тƂ������ԒP�ʂ𗘗p����B1/�т͑��x�ł��������炱�̑��x�� t ���Ԉړ�����Ƃ��̋��� X ���邢�� V �͎����Œ�`�ł���B
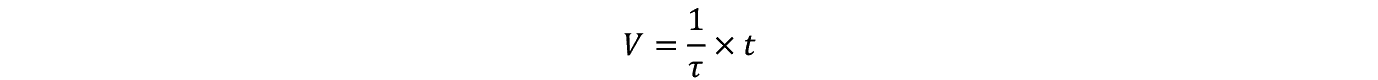
���������Ď��������藧�B
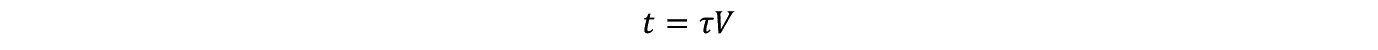
�������Ԃɂ��Ă�

�����藧�B
�܂�(33)�����̂悤�ɏ��������B
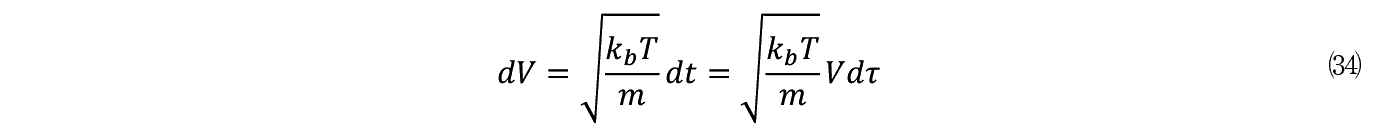
�����
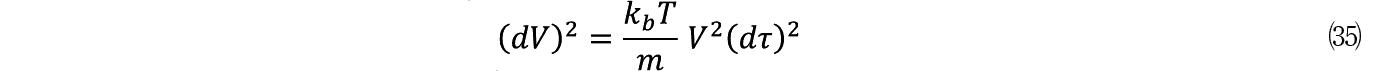
������⑻�̉��肩��

����������
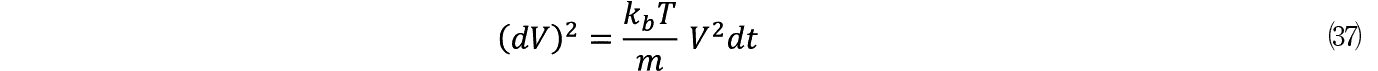
(32)��(37)�� dV �Ɓi dV �j 2 ��^����̂Ńu���E���^����\������������ʂ����B�����DXP�ł͊u���E���^�����Ӑ}�I�ɓ������Ă��邪�C V �� V 2 �̍��͂��̃��f���ł͕K�R�I��(32)��(37)�Ɍ���邱�Ƃɒ��ӂ��悤�B
���Ă����Ŕ����q�̃u���E���^����ݔ������s���ɉ��p����i�K�ɗ����B�����w�ł͔����q�̋K�i��\�ߌ��߂邱�Ƃ��ł��邪�C�o�ϊw�ł͓�����̂̋K�͂����̂悤�Ɍ��߂邱�Ƃ͂ł��Ȃ��B�u���E���^���ł͔����q�̑��x�ƈړ����������߂�Ƃ��C m �ƃ��Ƃ̔䗦�Ɉˑ����邱�Ƃ͊��Ɍ����B���������Čo�ϕ��͂ł������v���W�F�N�g�̎����I�Ȓ��g�����҂�����ł��邾���̃A�C�f�B�A�̏W�τ��ƁC������ȒP�ɂ͗e�F���Ȃ������̑g�D�Ƃ̝h�R�������ł��y108�Łz ����Ȃ���/ m �̑傫���ƂȂ邾�낤�B������/ m ���傫����i��R�����傫����j�����v���W�F�N�g�͒�~������Ȃ��B���������ē�������������ɂ́C�v���W�F�N�g�̒�Ď҂̐����͂��\���傫�����Ƃ������ł���B�����������ɂ͝����͂ɂ����铊�����T�|�[�g����O���[�v�����݂��邾�낤�B���̂Ƃ����ƂȂ�̂���ɏq�ׂ����͂ɂ����鐄�i�͂̑傫���ł���B�����\�������X�s�[�h���オ��Ȃ��Ƃ�����C�v���W�F�N�g���������� S �Ƃ����͂��K�v�ƂȂ�B
��q���������_���E�E�H�[�N���f���ŁC���B�_ Q �ɑ�������̂���Ƃ������ɂ���ĒB�����悤�Ƃ���ڕW��ƋK�͂ł���B�����Ńu���E���^���ɂ����ċ��� X �i t �j�Ƃ���Ă����ϐ���ݔ�������̂��ڕW�Ƃ���K�� V �i t �j�ƒu��������B���������_ t 0����̈ړ������ł���̂Ɠ����ɁC V �i t �j�� t 0����X�^�[�g���鎑�Y V �i0�j���B�����鎑�Y�K�͂ł���B�����_���E�E�H�[�N�̐�������ϓI���f�ŖڕW���߂�悤�ɁC�����ɂ����Ă̓P�C���Y�ȗ��̎�ϓI���f�������̖ڎw���ׂ��K�̈́�Ambition Level�������肷����̂ƍl���悤�B
����ɂ����ɂ����ăv���W�F�N�g�𐋍s�����ŁC�Q�̓������K�v�ƂȂ�B��P�̓v���W�F�N�g�̓��e�ɉ����������I�ݔ��̎擾�Ȃ����V�K�̌��݂ł���B���̂Ƃ��u���E���^���ɂ����Ĕ����q���������������ł�������Ɠ������̂��K�v�ł���B����ɓ�����̂��}−�Q�̂悤�ȗe��Ɨn�}�����C�����ɕ��͂ނ��߂ɂ͔�d�����ƂȂ�悤�ɁC�����ݔ��͓����Č�������ł���悤�ȏ���������Ă��Ȃ���Ȃ�Ȃ��B�܂�K�v�\���ȑ傫���Ƒϋv����ݔ������ɂ������Đ������Ȃ���Ȃ�Ȃ��B���̂悤�ȓ������������� I �Ə������Ƃɂ���BDXP���f���ł͓����z I �͑S���C�ӂ����C�u���E���^���ɑ������郉���_���l�X��O��Ƃ��铊���́C�����v���W�F�N�g�����サ�C�O�i���邽�߂̏����Ƃ������艻���K�v�ł���B
��Q�ɂ́C�O�q�̒��͂ɑ���������̂Ƃ��āC�lj��������ǂꂾ�����邩�̓I�v�V����������I�v�V�����������K�v�ƂȂ�BDXP�̋L���ł� F �i t �j�Ƃ���Ă���B������ F �i t �j�͓����Ƃ��ǂꂾ���̋K�͂� V �i t �j��B�����悤�Ƃ��Ă��邩�ŁC���̍œK�ȋK�͂����܂�B�A�������Č� V �i t �j���̂��̂������_���ȝ����͂ɎN����Ă���̂�����C�������߂�ɂ̓_�C�i�~�b�N�E�v���O���~���O�̎�@��Hamilton-Jacobi-Bellman���������K�v�ƂȂ�B
������ F �̖����́C�u���E���^���ł̒�R�͂ɑR���钣�͂ł���B F �ɂ���ď������� I �ł͕s�\���ł��������͂ɓ�����lj����������܂��B�����Ă��̎Љ�I�E�g�D�I�Ȓ�R���������邽�߂ɂȂ���铊���͌�߂�ł��Ȃ������̂��̂ł���B��U��Ă����Č������ł��P��i�Ē�āj�ł���Ȃ��R�͖����ɓ������B���������� F �Ƃ��������͕s�𐫁iirreversibility�j�����ƍl������B�܂� F �̓I�v�V�����ł͂��邪�C�s�t�I�ȓ����ł���C���ꂱ�����ݔ����������A���E�I�v�V�����̊j�S�ł���B�T���N�E�R�X�g�isunk cost�j�Ƃ������_���炷��C I �� F ���T���N�E�R�X�g�Ƃ������i�����s�t�I�����ł���B���ꂪ�F��̃y�����[�Y���ʂɑΉ����Ă��邱�Ƃ����炩�ł��낤�B�y�����[�Y�̊�Ɛ����_�ł͊�ƃX�y�V�t�B�b�N�ȓ����̏d�v�������グ���Ă��邪�C�����ł� F �͂܂��ɗՋ@�icontingent�j�ɕK�v�Ȍʂ̒����R�X�g�Ƃ��Ďx�o�������̂ł���B
�����Ŗ{�e�̓����̖ړI�ł���u�s�m�������̐ݔ������v�̎��_�ɂ��ĉ��߂Đ������Ă��y109�Łz �������B��{�I�Ș_�_�́C�l�X���s�m�����ɒ��ʂ���Ƃ��́C�ӎv����͎�ϓI�Ȃ��̂ɂȂ炴��Ȃ��Ƃ������Ƃł���B�x�C�Y�m�����m���������݂ł́C���̂悤�ȗ���͉���V��Ȃ��̂ł͂Ȃ��B���������j�I�Ɍ���Ύ�ϊm���͓`���I�Ȋm���_����ْ͈[�ƌ���Ă����B�܂��C�m���ߒ����和�Ƃ����I�v�V�������_��1970�N��ȍ~�Ɏs���������̂ɂ����Ȃ��B���̓_�ɂ��ċɂ��ȒP�ȓW�]�����Ă������B
�U−�P�@���͂̑O�j
�s�m�������̎��������̕��͂́C�s�m�������ǂ����͂��邩�Ƃ����ϓ_���猩��Ƃ��C�������̃G�|�b�N�ƂȂ錤��������B
⑴�@J.M.�P�C���Y�F��ʗ��_�i1936�j
�@�P�C���Y�́u��ʗ��_�v�Œ������ҁilong term expectation�j�Ƃ������_���瓊�������グ���B���̂Ƃ��j�S���Ȃ��Ă���̂���ƉƁientrepreneur�j�̎�ϓI�v�����݂ł���B�������邩���Ȃ����̌��f�͎�ϓI�m���Ɋ�Â��Ȃ���Εs�\�ł���Ƃ��āC�ganimal spirit�h�Ƃ�����g�������o���ꂽ�B���̍l�����ɂ��ăt�����N�E�����[�C�iFrank Ramsey�j�͂��̕s�O�ꂳ��ᔻ���x�C�Y�m���Ɋ�Â��ӎv����_�̕K�v���������咣�����B�����������[�C��27�Ś�܂������߂��̌�̔��W��Savage�m1954�n��҂��˂Ȃ�Ȃ������B
⑵�@G.B.Richardson: Information and Investment�i1960�j
�@�P�C���Y�Ȍ�C�������_�͑吨�Ƃ��Ă̓A�����J�E�P���u���b�W�̐V�ÓT�h���͂Ɏ���đ����C�P�C���Y�̐��_�͎���ꂽ�B�������C�M���X�ł̓��`���[�h�\�����P�C���Y��h����͓Ɨ����ĕs�m�����̖����u���v�ƌ��������C�����������L���ƂȂ�������l�����B���`���[�h�\���͐V�ÓT�h�I���S�����̐��E�ł́u�����v�Ƃ������ɒl����s���͓����Ȃ��Ƃ�������m�ɂ������߁C�V�ÓT�h�S���̎���ɂ͑S���ڂ݂��Ȃ������B���`���[�h�\���͐^�̊�ƉƓI�������Ȃ����ɂ́C�s��̕s���S���܂�Ɛ�I�s��̑��݂Ə��̕s���S�����܂�S�Ă̐l�������������L���邱�Ƃ͂Ȃ������������K�v�����ł���i�\�������ł͂Ȃ��j���Ƃ��ł��������j���Ă���B
⑶�@Jack Hirshleifer: Time, Uncertainty and Information�i1989�j
�@�n�[�V�����C�t�@�[�̓A�����J�ɂ����ĐV�ÓT�h�̗���ɉe�����ꂸ�����ƒ��~�̏������_���J���B���ɃA�[���B���O�E�t�B�b�V���[�ȗ��̓������_�ɕs�m����������ԑI�D�A�v���[�`�istate-preference approach�j�Ƃ��čč\�z���C���_�I���W�������炵�����V�ÓT�h�������_�iD.Jorgenson�Ȃǁj�Ƃ͓����قɂ��Ă��ď\���ɒ��ڂ���邱�Ƃ��Ȃ������B
⑷�@�u���b�N�E�V���[���Y�^�}�[�g���E�~���[�k1973�l
�@�������i�̓����������_���v���Z�X�ł���Ƒ�����ƁC�����w�̒m�������Z���i�̕��͂ɓ��Ă͂߂邱�Ƃ��ł���B���Z�I�v�V�����̗��_�́C�����_���E�E�H�[�N�̃A�C�f�B�A�Ɉɓ�����1942�N�ɔ��\�����m���ϕ������p����Ίm���Δ����������ɏW��ł����Ď��y110�Łz �Q���������ł��邽�߂ɁC�����������m��ł��邱�Ƃ���X�^�[�g�����B���ۊ����͔����q�������q�Ƃ��������̈��q�̈��͂��đS���\�z�s�\�ȓ���������̂Ɠ�������������B���A���E�I�v�V�������_��DXP�����Z�I�v�V�����̃��f���̍��i���������Y�ɂ��̂܂܉��p�ł�����̂Ƃ��ăX�^�[�g�����B
�U−�Q�@��ϓI�������ӂƕs���_
DXP���f���̓u���b�N�E�V���[���Y�̎�@�P���ăI�v�V�����l�����߂邱�Ƃɕ��͂��W�����Ă���B���̌��ʁC�Δ����������̉������̂܂��������ɂ��u����������ƍl�����B�ǂ̂悤�Ȕ��z�����𐳓����ł���̂��ɂ��Ă͐G��Ă��Ȃ��B�������x���}���������ɂ���ĉ���Ƃ����ȑO�ɁC�ȉ��̂悤�Ȏv�l�v���Z�X���K�v�ł���B
�u�|�����̚�̎v�l�����v
⑴�@������͎̂����𓊓�����O�i�K�ł������̓����@��Č����r��������B�����ē�������̂́u�����n�ɏ��v���Ƃ��K�v�ł���B������̂͂����������Č�−−�A�C�f�B�A�̃|�[�g�t�H���I���r���Đ����̃x�C�Y�m�������Ȃ��Ƃ�1/2�ȏ�̂��̂�I�ʂ���ł��낤�B���̂��Ƃ��������̂Ɂu�|�����̚�v���邢�́gurn�hproblem���Љ�悤�B
�gurn�hproblem�Ƃ����͎̂��̂悤�Ȏv�l�����ł���B
�F���܂Q�́u��v�������āC���ʂƔ��ʂ������Ă���B���̔䗦�͈ȉ��̂悤�Ɏ��O�ɂ킩���Ă���B
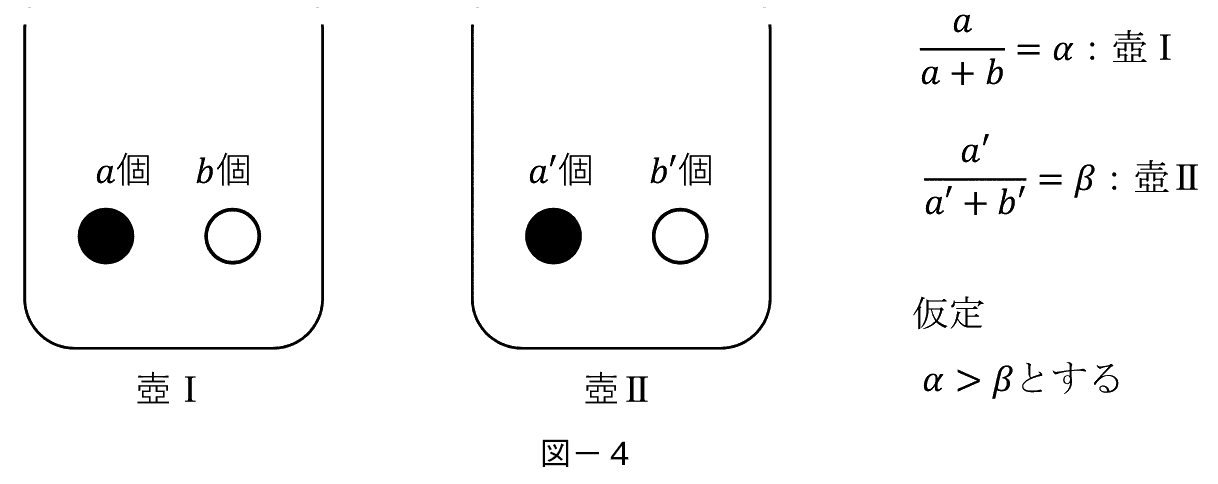
���ʁC���ʂ͓����v���W�F�N�g�̃|�[�g�t�H���I�������Ă��āC���͏������̍����A�C�f�B�A�C���͂��܂�L�]�ł͂Ȃ��A�C�f�B�A���w���Ƃ��悤�B�Q�́u��v���ׂĂǂ���́u��v��I�Ԃ��Ƃ����C�u��v���̍��ʂƔ��ʂ̔䗦���ŏ��ɂ킩���Ă��ĂQ��P���ɔ�ׂ���Ȃ獕�̑������̂ق��i�u��v�T�j���̗p����̂����R�ł���B�����������ɕs�m����������B�u��v�T�ƇU�Ƃ��������悤�Ƃ��Ă���l�ɂƂ��Ċm���I�ɂ�������Ȃ��Ƃ��悤�B�܂�T�ƇU�Ƃ���Ɋ�O�ɂ���̂ł͂Ȃ��ćT�ƇU�Ƃɑ�������̂͊m���I���Ƃ���̂ł���i����͏�ɂ��邱�ƂŁC�u�߂��荇���v�͊m���I�Ȍ��ۂł���j�B
�����Łu��v�T�ɂ߂��荇���m���� X �C�u��v�U�ɂ߂��荇���m���� Y �Ƃ���B����ƍ����y111�Łz �T������o���m���ƇU������o���m���̓x�C�Y�m���Ōv�Z�ł���B
�E�T���獕���o��x�C�Y�m�� B�T
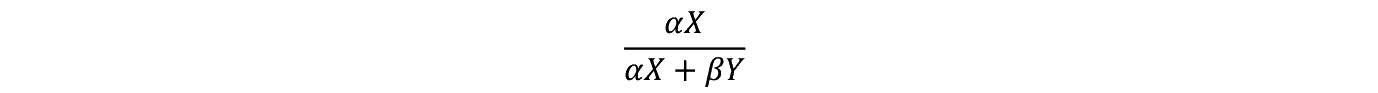
�E�U���獕���o��x�C�Y�m�� B�U
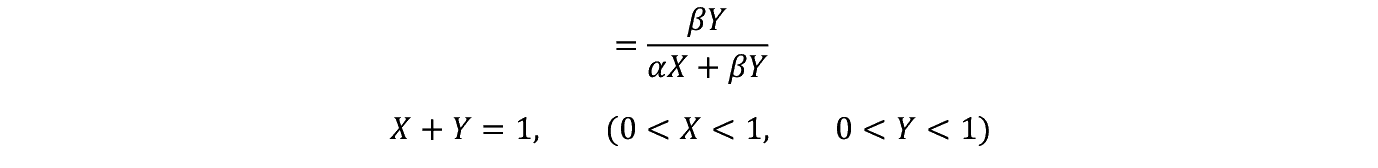
B�T��B�U���ׂ��
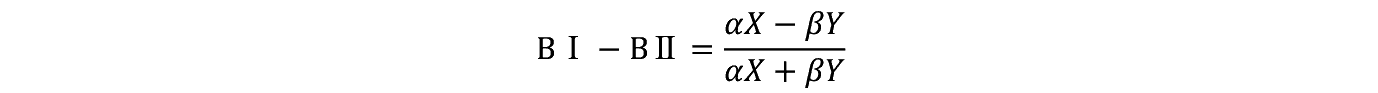
B�T>B�U�ł��邽�߂ɂ�
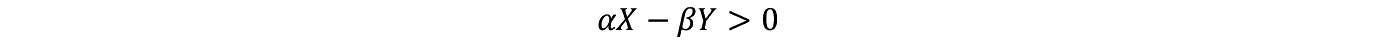
��>�� �Ȃ̂� X > Y �Ȃ���
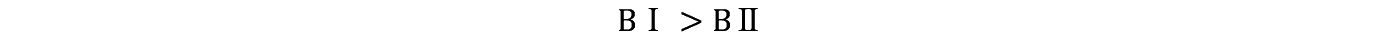
�ƂȂ�C�T����o��m���������B
X > Y �Ƃ�X > 1/2�Ƃ������ƂŁCX > 1/2�Ƃ����\������������·T���I�������BX >1/2��K�v�����Ƃ�����T��I�Ԃ��Ƃ����������̂ł��̎v�l�����ɂ͈Ӗ����Ȃ��B�ڍׂ͏Ȃ����u�|�����̚�v���ł͎i��҂����Ċϋq�ɚ₩��ʂ����X�Ɏ��o���u���i���j���o����ǂ���̚₩��o�����v����������ł���i�J�[�e���Ś₩����o���p�͌����Ȃ��j�B�����ł́u������v���Ƃ��ǂ��炩��I�Ԃ��Ƃ��Ӗ�����Ƃ��悤�B�܂肱��́u�߂��荇���v�Ɠ����\���������Ă���B�����i��҂������_���Ɂu��v��I��ł���Ȃ�i X �� Y ��1/2�j�C��̗�Ɠ����œ����͇T�Ɍ��܂��Ă���B�������i��҂ɂ͕Ό��������� >���Ȃ����̂ق����ۛ����āu��v�T�����o���₷���Ƃ��悤�B����� X �̏o������x�C�Y�m���̂ق��� Y ��荂���Ȃ�B����̓P�C���Y�̔��l���[�̗�Ɠ����ł���B�����i��҂���ʐ��_���\���Ă���Ƃ���Ƃ݂�Ȃ������Ǝv���ق��ɓ��[����̂Ɠ����s�������Ă��邩��ł���B��ϊm���ɏ]���ăv���W�F�N�g��I�ԂƂ����̂̓x�C�Y�m���ɏ]���ē����Ƃ��s�����鎖���Ӗ�����B
⑵�@�����Ƃ͈Č��̉��l������̎��Y V �i t �j�����Đ�������B�܂�m���I�ɕϓ�����v���W�F�N�g�̔��W�X�s�[�h���r���C���� v �i0�j���\���傫��������������B v �i0�j�����ɒႢ�Ƃ��͖����ł��邩��C���鐅���ȏ�ɓ��B�����Ƃ�������� V 0�Ƃ��鄟���X�^�[�g�Ƃ��āC�����ɂ��āu���v��`���B���̖����P�C���Y�̌����u�A�j�}���E�X�s���b�g�v�̌���ł���B�}–�P�͂��̂悤�ȓ�����̂������Ώۂɑ��ĕ`���|�W�e�B�u�ȗ\�z�� V �i t �j�̔��W�O����`�������̂ł���B������u���]�v�Ȑ�  �ƌĂԂ��Ƃɂ���B
�ƌĂԂ��Ƃɂ���B
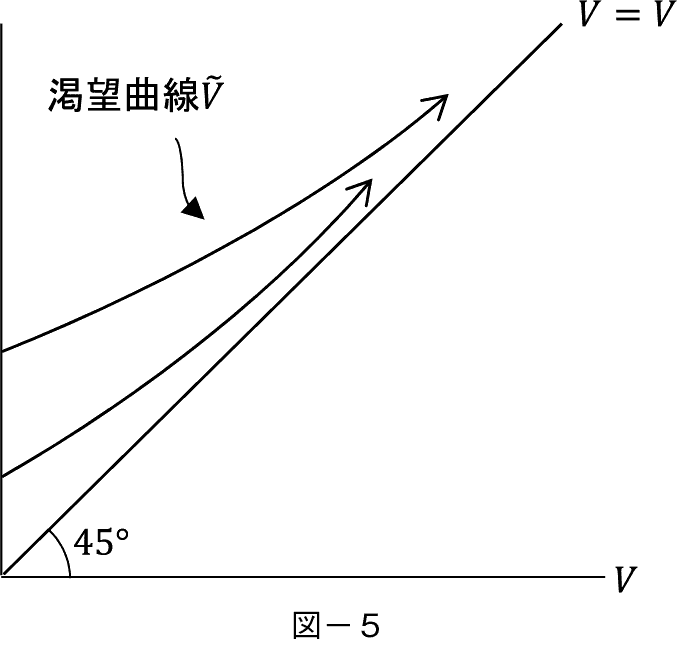
�}�� V �� V ��45�����������C 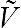 �͂Q�̃^�C�v�̂��̂�`���Ă���B
�͂Q�̃^�C�v�̂��̂�`���Ă���B
�����Ƃ͓��R�Č� V �i t �j�̒��g���܂���������B����̓����W���o���������̗�ł́C���͂܂��d��S���W���ׂ邱�Ƃɓ�����B����Ŕ[��������ɏ����x v �i0�j��^����t���[�E�L���b�V�� I �̓��������f����B���̂Ƃ������Ƃ͎��̂悤�ɗ\�z�𗧂Ă�Ƃ��悤�B
�ώ@����� V �i t �j�̒l�ɑ��C�����Ƃ���S�������ł���悤�� V �i t �j�̗\�z�l�܂芉�]�l�� 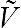 �i t �j�Ƃ���Η��҂ɂ͎��̎ʑ��W���z��ł���Ƃ���B
�i t �j�Ƃ���Η��҂ɂ͎��̎ʑ��W���z��ł���Ƃ���B
Vti�̊ώ@�ɂ����  ti �͕ω����C�����ƂɂƂ��Ă̖�S�������ł���悤�ȗ\�z�Ȑ���}−�T�̂悤�ɕ`����B���ꂪ�u���]�v�Ȑ��ł���B
ti �͕ω����C�����ƂɂƂ��Ă̖�S�������ł���悤�ȗ\�z�Ȑ���}−�T�̂悤�ɕ`����B���ꂪ�u���]�v�Ȑ��ł���B
���� 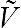 �Ȑ��� V �� V �Ƃ���45�����ɑQ�߂��Ă����CDXP��smooth pasting�����肳���C�����ꂩ�̈ʒu�� V �����ɐڂ���5�j�B���̐ڂ���ʒu���C������̂̏����ɑ��銉�]�̐���
�Ȑ��� V �� V �Ƃ���45�����ɑQ�߂��Ă����CDXP��smooth pasting�����肳���C�����ꂩ�̈ʒu�� V �����ɐڂ���5�j�B���̐ڂ���ʒu���C������̂̏����ɑ��銉�]�̐��� 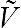 �������Ă���B
����������B
⑶�@���]�̐����͏����̓����z I ���^������Ƃ��C���R���鐅���Ɏ������Ȃ���Ȃ�Ȃ��B���Ȃ킿 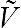 �̎��Ȏʑ��ƂȂ� V �̐��� V �� �����݂���B�����
�̎��Ȏʑ��ƂȂ� V �̐��� V �� �����݂���B����� 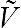 �̌��E������ ∆
�̌��E������ ∆ 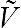 /∆ V �ɂ��� V ���������Ă��C���͂�
/∆ V �ɂ��� V ���������Ă��C���͂� 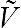 �͑������Ȃ��Ƃ����_���Ȃ���Ȃ�Ȃ�����ł���B�����łȂ����
�͑������Ȃ��Ƃ����_���Ȃ���Ȃ�Ȃ�����ł���B�����łȂ���� 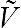 �̑������i���ɑ����Ɖ��肷�邱�ƂɂȂ�C���܂Ōo���Ă������̌��f�@��͖K��Ȃ��B
�̑������i���ɑ����Ɖ��肷�邱�ƂɂȂ�C���܂Ōo���Ă������̌��f�@��͖K��Ȃ��B
�܂�
�y113�Łz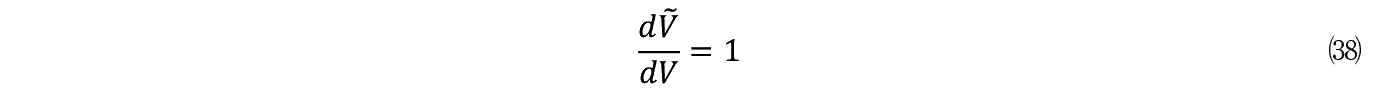
�Ƃ����_�ŕs���_�����肳���B�����}�������̂����}�ł���B
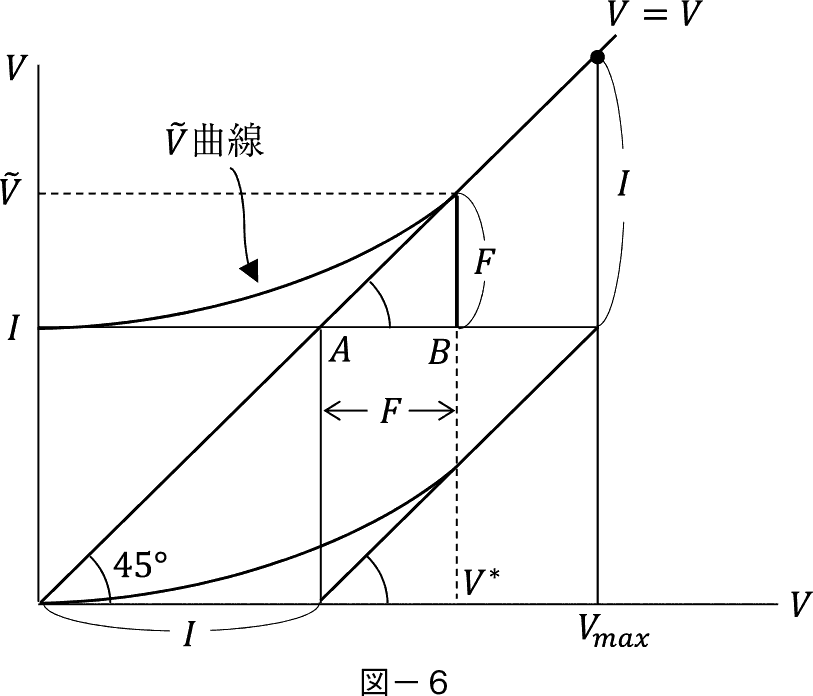
V �� I ����X�^�[�g���銉�]�Ȑ��̌X����45������ V �� V �Ɛڂ���Ƃ��C V �̑������� 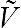 �̑������Ɠ������Ȃ�B�}−�U�ŁC I �ɒlj�����铊���zAB�� F �Ƃ���� F �{ I �ɂ���ĕs���_
�̑������Ɠ������Ȃ�B�}−�U�ŁC I �ɒlj�����铊���zAB�� F �Ƃ���� F �{ I �ɂ���ĕs���_ 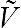 ����������B�����
����������B�����  �Ȑ��� I ���������փV�t�g������� I ���������45������
�Ȑ��� I ���������փV�t�g������� I ���������45������ 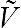 �Ȑ��Ƃ̐ړ_�� V �� ��������B�����ăX�^�[�g���_�ł̓�����̂̏����]�l�i
�Ȑ��Ƃ̐ړ_�� V �� ��������B�����ăX�^�[�g���_�ł̓�����̂̏����]�l�i 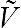 − I �j�̌`��ɉ����Ď��Ȏʑ��ƂȂ�s���_�����܂�C�}−�U�ł͂��ꂪ V �� �ł���B���������� I �ɑ���lj������z�� V �� − I �� F �ł���C�������zK��
− I �j�̌`��ɉ����Ď��Ȏʑ��ƂȂ�s���_�����܂�C�}−�U�ł͂��ꂪ V �� �ł���B���������� I �ɑ���lj������z�� V �� − I �� F �ł���C�������zK��
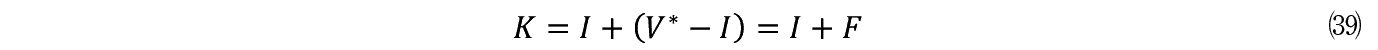
�Ǝ������B
�ȏ�ɂ���Ď�ϊm�����������Ċ��]�Ȑ��Ɩ��t���� 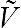 �܂���
�܂��� 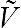 − I ��45�����̐ړ_���s���_���������߂邱�Ƃ��킩�����B����������͈�̋��b�ł����Ēlj������ł��� F �i�� V �� −1�j�̋�̓I�����͌���ł��Ȃ��B�����ɂ����ă_�C�i�~�b�N�E�v���O���~���O�iDP�j�̎�@�ōœK�� F �����߂Ȃ���Ȃ�Ȃ��B
− I ��45�����̐ړ_���s���_���������߂邱�Ƃ��킩�����B����������͈�̋��b�ł����Ēlj������ł��� F �i�� V �� −1�j�̋�̓I�����͌���ł��Ȃ��B�����ɂ����ă_�C�i�~�b�N�E�v���O���~���O�iDP�j�̎�@�ōœK�� F �����߂Ȃ���Ȃ�Ȃ��B
���{�\�Z�I�ɍl����C I �Ƃ͗\�߉�������҂��Ă��Ȃ��t���[�E�L���b�V���E�t���[����x�o�������̂ł���B�x�C�Y�m���Ŕ��f���Ă��铊���Ƃ́CX > Y �Ƃ��������͖�������Ȃ��Ƃ��Ă��C����͊o�債�Ă��邩��ł���B�����O��Ƃ��Ēlj����� F ���K�v�ƂȂ邪�C�y114�Łz
����͓����v���W�F�N�g V ���ǂꂾ���L�]���Ɉˑ�����B�t���[�E�L���b�V�� I �͓����Č������C���̐g�̏䂪���܂�ƒ�z���x�o����邪�C F �͂ǂꂾ���x�o���邩�ɂ��ăI�v�V����������B�����������Č��̏��� v �i0�j���\���ɑ傫����C������ I �𓊉����邱�Ƃ��ł���B���̂Ƃ��I�v�V�����̓[���ł���B�������v��͗L�]�����s�m����������C����҂��Ēlj��x�o F ������ 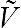 ������������Ƃ�����ϓI�Ȕ��f���������́C F ��������o�����Ƃ����I�v�V������������B����������C�s�m�������L�]���Ƃ����v���W�F�N�g�ł́C���̊W�����藧�B
������������Ƃ�����ϓI�Ȕ��f���������́C F ��������o�����Ƃ����I�v�V������������B����������C�s�m�������L�]���Ƃ����v���W�F�N�g�ł́C���̊W�����藧�B
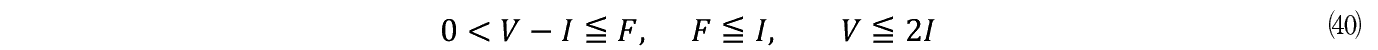
V �� I ������Ȃ���Βlj������͈Ӗ��������Ȃ����C���̑傫���͒lj����� F �������łȂ���Ȃ�Ȃ��B�Ȃ��Ȃ� V − I �� F �����傫���Ȃ�C���� I �Ƃ��������z�� V �ɑ��ď���������̂ł���C���̎��͂����Ƒ傫�� V ���ŏ��ɑI�Ԃׂ�������ł���B
�m���I�ɕϓ����Ă��铊���v���W�F�N�g�̓��������Ȃ���C�lj��I�ɓ�������Ƃ����I�v�V�������o�ϓI�ł���Ɣ��f�����Ƃ��C��ƉƂ͒lj����� F �����肷��B�܂�I�v�V�����͓����R�X�g�ł���Ɠ����ɐϋɓI�ɓ�������ӗ~�̂��铊���Ƃ��v���W�F�N�g V �ɗ^�����ϓI�Ȍ��p�ł���B
�����ŃI�v�V�����l�Ƃ��Ă��� F �́C�����W���o���������̘g�g�݂ɓ��Ă͂߂�ƒ��� S �ɑ������邱�Ƃ��m�F���Ă������B���C��R�ɂ���đ����ɒ�~��������q�ɑ��Ē��͂������ĉ����x�����C�����q����i�����邱�Ƃ��ł���̂����Ɍ����B����𓊎����f���Ƃ��Č���Ə���R�ɂ���ē������ڍ�����̂�h�����߂ɒlj����� F ���x�o�����B����͖��C��R�Ƃ��������̃��X�N�����E����̂ɕK�v�ȃR�X�g�ł���B�����W���o���E���f���ł̓��Ƃ������i�̃��X�N���ɂ������E����̂Ń��X�N�̓�−�ɂɏk������̂ł���B�����Ă�艓���܂ŕ��i����ߒ��ł͗h���͂������Ĕ����q�͂��̕��O�i�ł���B�ȏ�̂悤�ȃv���Z�X��DP�ɂ���� F �̍œK�l�����߂悤�BDP�ł� V �i t �j�ɂ���HJB��������p���邱�Ƃ��ł��邪�C�����ł�DXP�̂悤�ɒ��� V − I �ł��� F �i t �j�ɂ��ăx���}���������𗘗p���邱�Ƃɂ��悤6�j�B���̂ق����h���͂̌��ʂ����₷������ł���B
�x���}���������Ƃ͎��̂悤�ɏ�����B
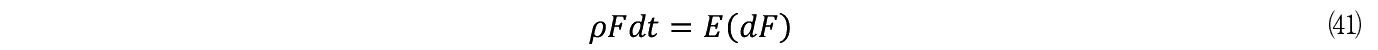
�����œ����Ƃ̎�ϓI�Ȏ��Ԋ������ς�����B����ɂ���č����̒lj�����Ft�������� F t�{1�j�Ɠ������]������C����ȏ�͒lj������̑����͖]�܂Ȃ��Ƃ����������ݒ�ł���B�܂�ς͍ő�̊��Ҏ��v���ł�����B
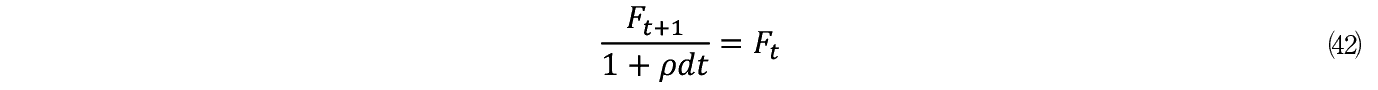
(42)���� F �̍��� dF �͎��̂悤�ɂȂ�B
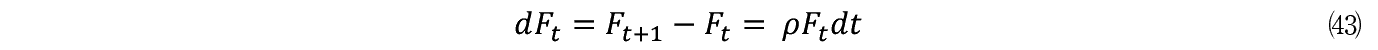
������ Ft �͊m���ϐ��ł���C���̊��Ғl E ���Ƃ�B
����� dFt ���e�C���[�W�J�����
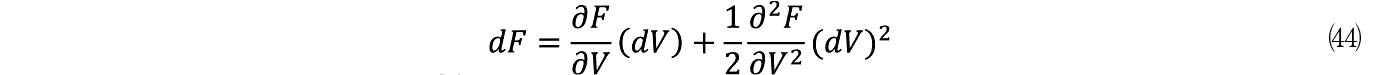 �y115�Łz
�y115�Łz
(44)�� dV �Ɓi dV �j 2 �̓����W���o���������̉����狁�߂�ꂽ(32)��(37)�ł���B
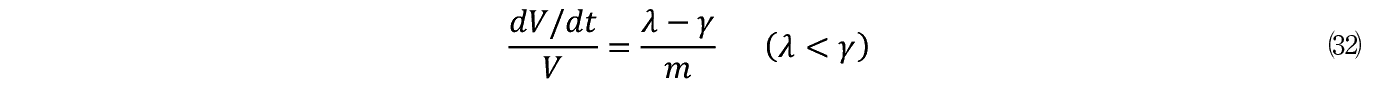
(32)����
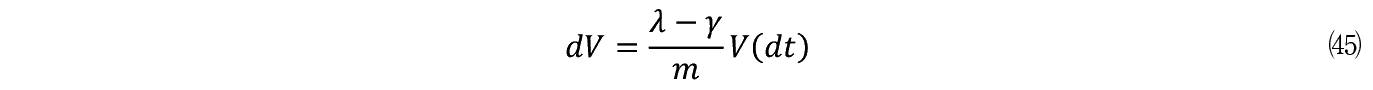
(37)����

�ȏォ��ɓ��ߒ���V������'�C�ӂōĒ�`���悤�B
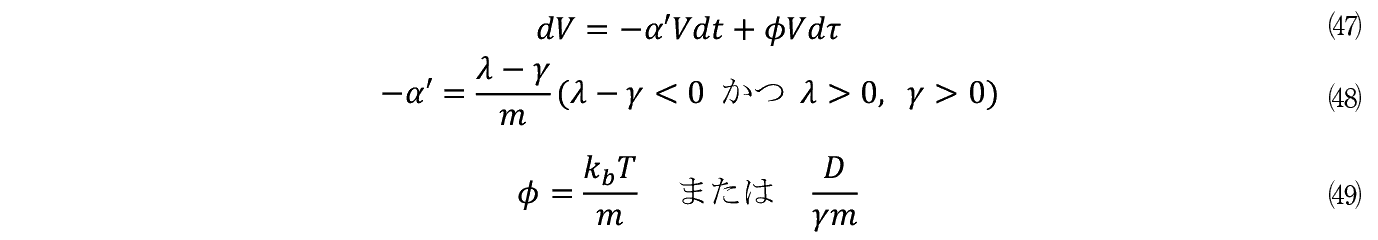
������(47)�͊u���E���^�������肵�Ă���̂ł͂Ȃ�(32)��(37)���瓱�������̂ł��邱�Ƃɒ��ӂ��˂Ȃ�Ȃ��B
(43)���͎��̂悤�ɏ�����B
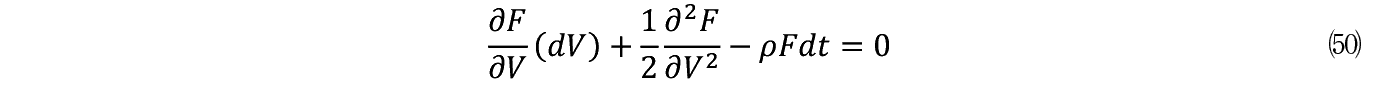
����͐Ď��Q�K�����������Ȃ̂Ŏ������ƂȂ邱�Ƃ��킩���Ă���B
�@�@�@�@�@�@�@�@�@�@�@�@�@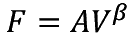 7�j
�@�i A �͒萔�j�@�@�@�@�@�@�@�@(51)
7�j
�@�i A �͒萔�j�@�@�@�@�@�@�@�@(51)
���̂��Ƃ𗘗p����(51)��(50)�ɑ�����Čv�Z����ƃ��ɂ��Ă̓�����������������B
���̓����������͎��̃��̂Q�����ł���B(50)�� dt �͏��������̂ʼn��͒����̐��i�����B
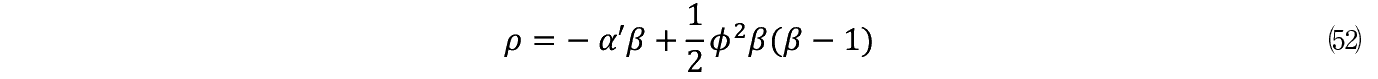
���͎��̂悤�ɒe�͐��ƂȂ��Ă���B
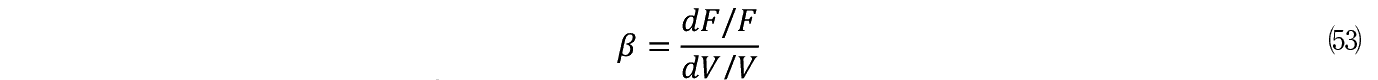
���Ȃ킿 V ���P�����������邽�߂ɂ́C�lj����� F �������K�v���������Ă���̂ŁC�����̌��E��p�ƌĂ�ł悢�B
���Ă����Ŏ��̂��Ƃɒ��ڂ��悤�B(52)�̍��ӂ͎��Ԋ����������C�����ɓ����̌��E���v�����\�킵�Ă���B����E�ӂ̓��̂Q�����Ŏ�����铊���̌��E��p�ł���B�E�ӂ̑�P���́C−��'�Ƃ������C�ɒ��ʂ��郊�X�N�����������C��Q���͓������v�b�V������h���͂����������ł���B�܂�E�ӂ͐��Ɋ�ƉƂ̃��X�N�E�e�[�L���O�̎p��\���������̂ɊO�Ȃ�Ȃ��B
F �̒l�̓��̓����������̉�����������߂�(51)�ɑ������Γ�����B
�y116�Łz���̌��胁�J�j�Y���������ɂ���Č��邱�Ƃ��ł���B(52)�̉E�ӂ�
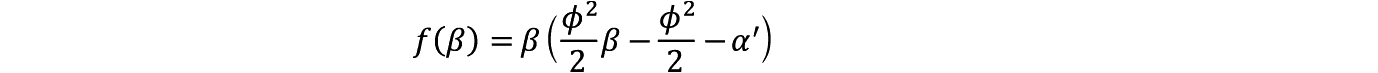
f �i���j�͎������藧�B
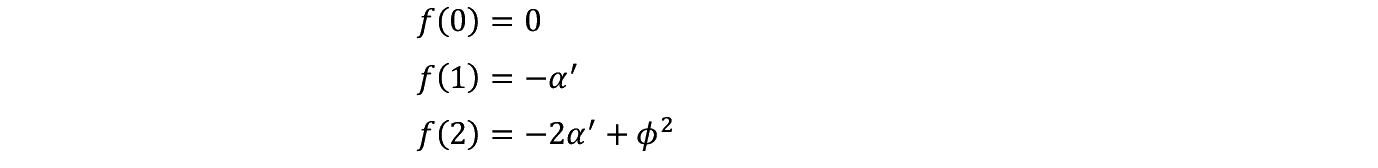
��� f '�i���j��0 ������̍ŏ��l 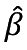 ��
�� 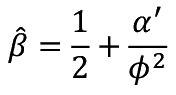
���͌�q����悤�ɂQ�ȏ�̕K�v������B���̗̈�Ńς� f �i���j�ƌ�_�������߂ɂ�
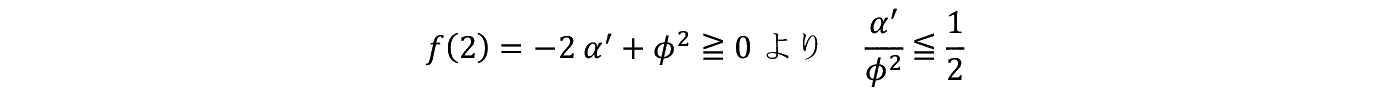
����������
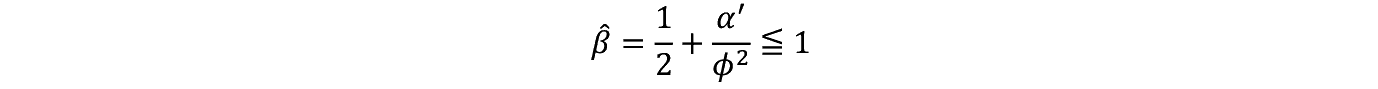
�ȏ���� f �i���j���͈ȉ��̂悤�Ȍ`���Ƃ�B
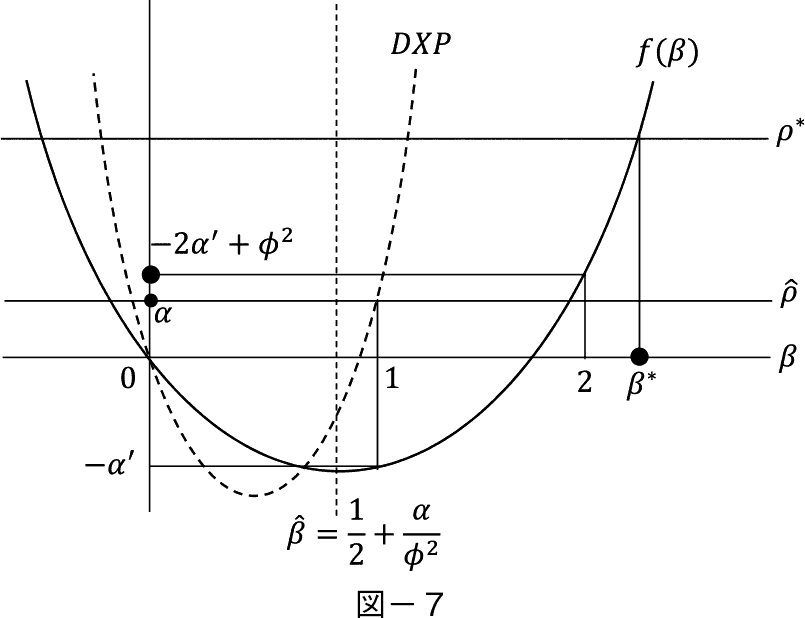
�}−�V�Ńς� f �i���j�Ƃ̌�_�͌��E���v�������E��p�ƈ�v����_�ł���B�����Đ}−�V�Ńς��� �� �ł���Ƃ��C���E���v�������E��p�ƂȂ�� �� �������������̉��ƂȂ�B
������DXP�Ɣ�r���悤�BDXP�ł�(52)�ɑ�������̂������ł���B
�����}������Ɛ}−�V�̔j���ƂȂ�B���̂Ƃ���=�P�� �����ƂȂ�ςƌ��E��p�Ƃ̌�_�͂P<��<�Q�ł����݂���B�Ƃ��낪�}−�W���炱�̂Ƃ��� F �� I ���傫���Ȃ�B�܂� F �� I �Ƃ����\�Z������Ȃ��̈���܂ށB���������� F �͂�����ł��傫���Ȃ��Ƃ����y117�Łz
������������Ȃ��B
�����ƂȂ�ςƌ��E��p�Ƃ̌�_�͂P<��<�Q�ł����݂���B�Ƃ��낪�}−�W���炱�̂Ƃ��� F �� I ���傫���Ȃ�B�܂� F �� I �Ƃ����\�Z������Ȃ��̈���܂ށB���������� F �͂�����ł��傫���Ȃ��Ƃ����y117�Łz
������������Ȃ��B
���ă� �� �ɂ���čœK�Ȓlj������z���邢�̓I�v�V�����l F ��
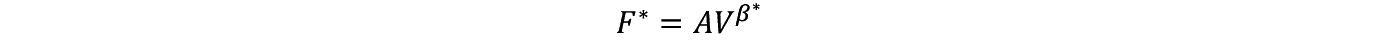
�ŗ^������B
���̂悤�ɂ��� F �� �����܂�ƁC��Ƃ̓����ڕW�ł��� 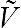 ���邢�͍œK�ȓ����z V �� �����̂悤�ɏ�����B
���邢�͍œK�ȓ����z V �� �����̂悤�ɏ�����B
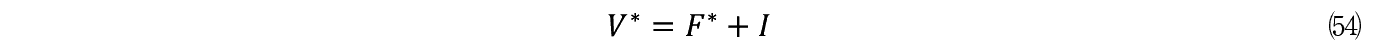
���̒l�͗\�Z��������ƂƂ��ɁC��ϓI�œK����������s���_�Ƃ��Ȃ��Ă���B(51) (54)����
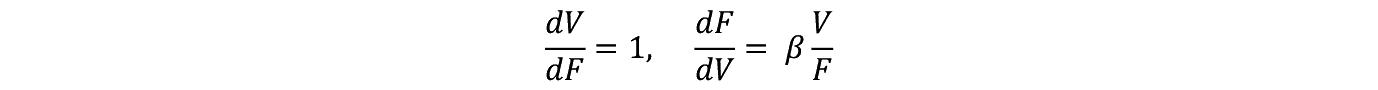
������(54)�ɑ�����Đ�������Ǝ��������藧�B
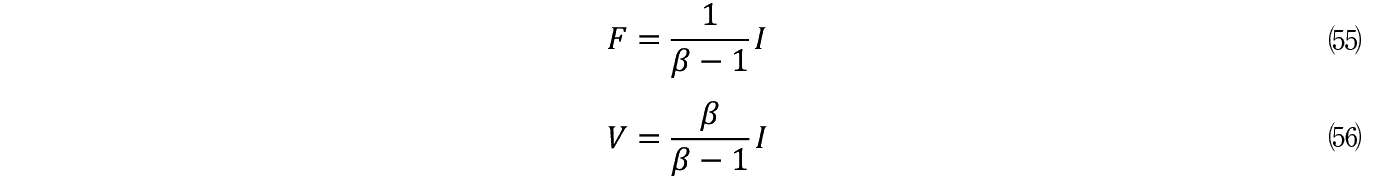
���Ȃ킿 F �� V �� I ��p���ĕ\������Ă���B I �ƃ����^������� F �����܂郁�J�j�Y���́C�}−�W�Ɏ�����Ă���B
����ɒ萔 A ��
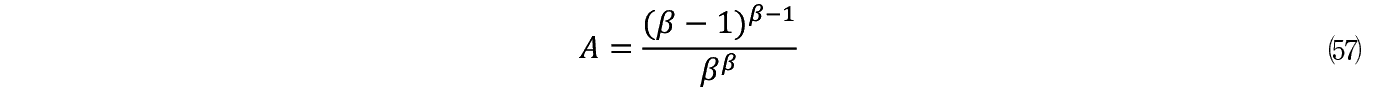
���͒e�͐��Ƃ��ĕ\����邪�����ɕs���_�ł͎������藧�B
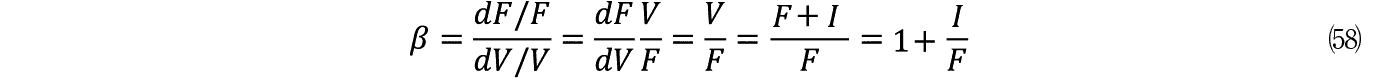
I �� F �Ƃ����\�Z����
�@�@�@�@�@�@�@�@�@�@�@�@�����Q�@�@�@�@�@�@�@�@�@(59)
�܂�e�͐������E��p�ł�����͂Q�ȏ�ł���K�v������B
�����Ŋe�p�����[�^�̔�r�Êw���s���Ă݂悤�B�܂����ɑ��Ċe�p�����[�^�̕��������͈ȉ��̒ʂ�ł���B
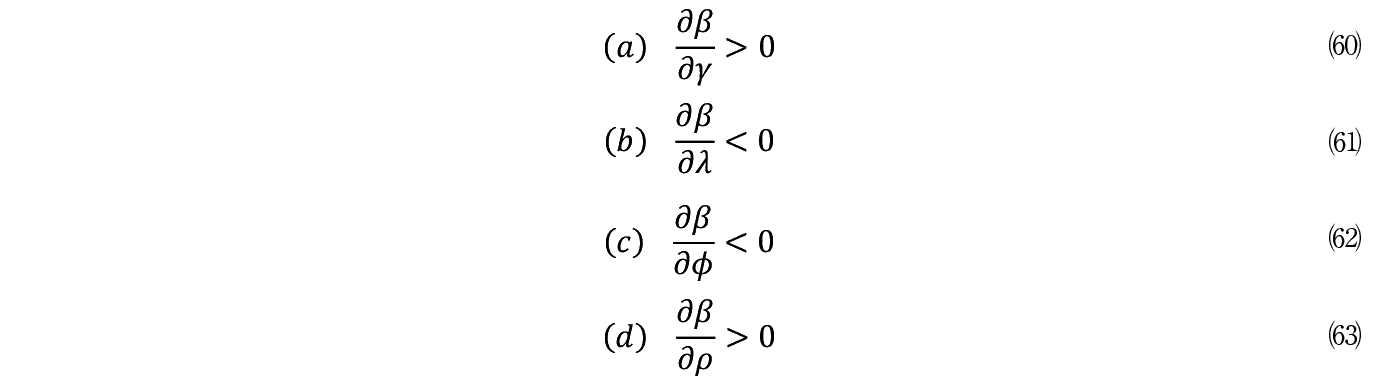 �y118�Łz
�y118�Łz
F ��(55)�ɂ���ă��ŕ\����̂ŁC���� F �ɗ^������ʂ͎��̂悤�ɐ}−�V���猩�邱�Ƃ��ł���B�Ⴆ�Ί������ς���1�̂Ƃ����̒l�̓�1�ƂȂ�B���̃�1�ɑ��Ă͉��}�� F �Ń�1�ɑΉ�����c����� F ���� F 1�����܂�B��2�̂Ƃ��͓��l�Ƀ�2�ɑΉ����ĉ��}�� F 2����܂�B�����Ŋe�p�����[�^���ŏI�I�� F �ɗ^������ʂ��ȉ��̂悤�Ɍ��肳���B
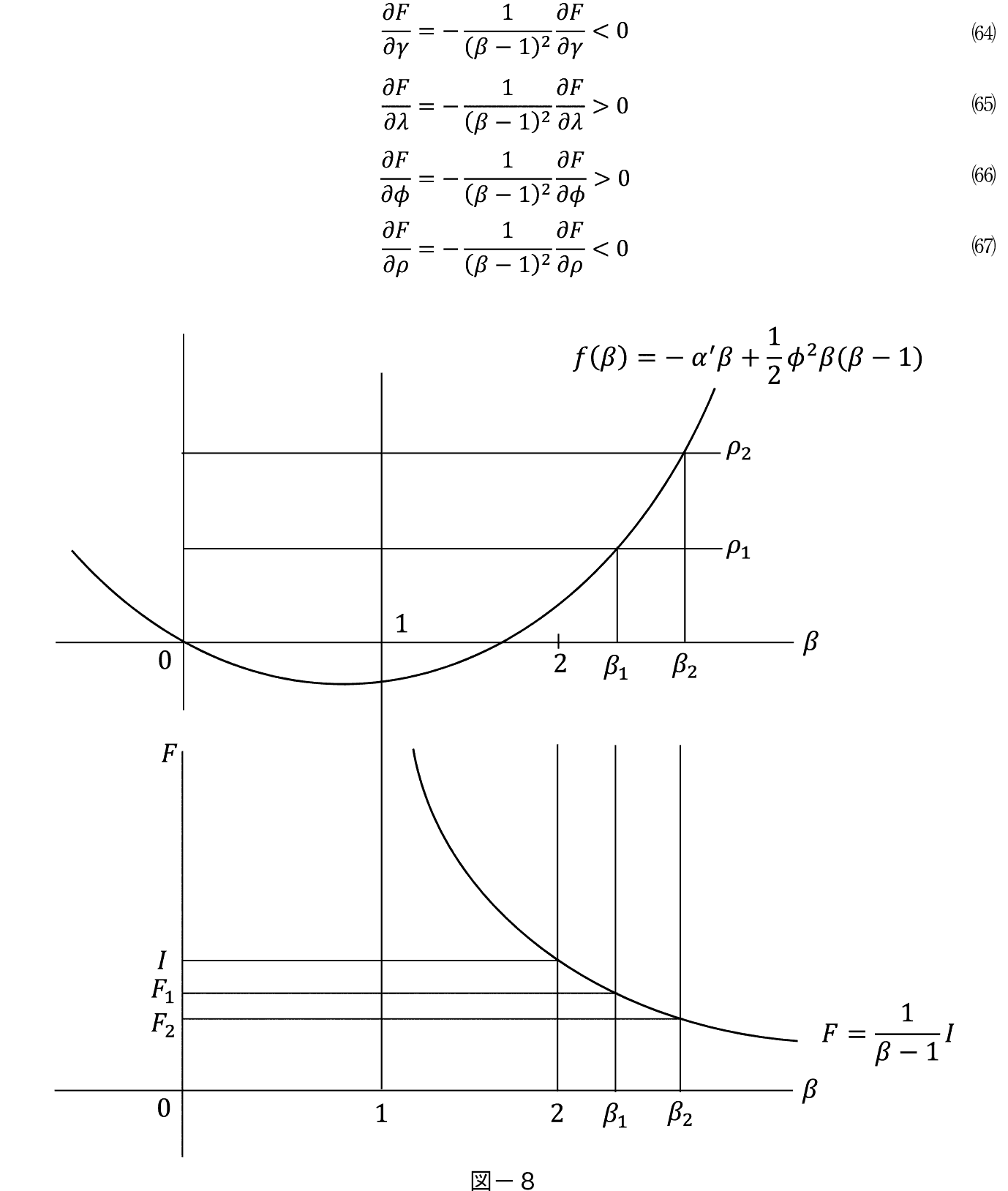
�ȏ�̊e�p�����[�^�� F �ɗ^����܈ӂ����ɗv��B
�i�@�j�܂����Ɏ��������i���̂ƌ��������j�ɂ͖��C�́i���j�̒�R���K�����݂���B���̖��C�͂��傫���قǕs�m�����͍��܂�lj������̃��X�N���傫���Ȃ�̂œ����C���Z���e�B�u�͉�������B������������̂�(64)�ł���B
�i�A�j���������̖��C�ɂ���ē�������~���Ă��܂�Ȃ��悤�ɁC��R���ɘa���邽�߂̊����i�Ɂj���Ȃ����B��R���͂Ɛ키�̓ɂ��L���Ȃقǒlj������͑��傷��B���ꂪ(65)�ł���B
�i�B�j(66)�̃ӂŎ����ꂽ���̂̓����_���͂������Ă���Ƃ��C�����炳���n�̂�炬 D ���邢�� kbT �Ŏ������M�ʂł���B�����DXP�ł̃Ђ̂悤�ȃ��X�N�ł͂Ȃ��B�����_���ȗ͂͗h���͂ƂȂ�C�S�̂̌n���h������B���̑傫���͕����I�ɂ� kbT �i�{���c�}���W���~��Ή��x�j �����C�ݔ������̃R���e�N�X�g�Ō���Ƃ��́C�������̎���́u�M�C�v��u����オ��v�ƍl���Ă悢���낤�B�܂�ɂƂ������X�N�������Ď��C���Z���e�B�u�͋����Ȃ�B���̃ӂ��傫���قǓ��� F ���傫���Ȃ�B���{�́u����ꂽ20�N�v���l����ƁC�ݔ�����������2000�N��O�����玸�������̂́C���{�o�ρE�Љ�̎���ꂽ���C�������ł͂Ȃ��낤���B�����w�� kbT �Ƃ����l�͗��z�C�̘_���瓱�o����钊�ۊT�O�����C�geconomy�h���ЂƂ̑傫�Ȍn�ƌ���C���C�̂Ȃ����{�Љ�̕a��Əے��I�ȑΉ�������ƍl���Ă悢���낤�B�܂�s�m�����̐��E�ł͎��������͔M�C�̗��_�Ȃ̂ł���B
�i�C�j���Ԋ������������قǓ�������������Ƃ���(67)�̈Ӗ�����̂́C�o�σV�X�e������苣���I�ɂȂ�قǁC�������ߎ���I�imyopic�j�ɂȂ邱�ƂɑΉ����Ă���B�����Richardson���g�ɋ������Ă���_�_�ł���BRichardson�ɂ��Ί����ȓ����Ǝs��̓Ɛ�I�v�f�Ƃ̊W��Marshall�����Ɏw�E���Ă����Ƃ��낾�Ƃ����B�V�ÓT�h���f���ł̓��X�N�����������I�ł���قǓ����������ƂȂ�Ƃ������펯�I�Ȍ��ʂ�8�j�������W���o���������̐ݔ��������f���͋t�̌��ʂ�^����ƌ�����B
�ȏォ��s�m�������u���E���^���ɂ���ē����������������f���͐V�ÓT�h���f���ƑΏƓI�Ȍ��ʂ�^���邱�Ƃ��킩��B���ɕ��U�̍��͒ʏ탊�X�N�Ƒ������邪�C����͋t�ƂȂ�|�W�e�B�u�ȈӖ��ł́gfluctuation�ł����ĔM�C�Ɖ��߂��ׂ����̂Ȃ̂ł���B
�����ōŏI�I�ɓ���ꂽ�����s���̌o�ϓI�ȈӖ������ɂ��āC�F��E�y�����[�Y���ʂƂ̊֘A���w�E���Ă������BUzawa�m1969�n�ł̓}�N���̐������f���̃R���e�N�X�g�Ńy�����[�Y���ʂ���������Ă���B����͊�Ƃ����V�X�e������V�V�X�e���ւƊ�Ƃ��ڍs����Ƃ��ɂ́C�������K�v�����R�X�g��ƋK�͂傳����ɂ͓����R�X�g�͒������Ȃ���Ȃ�Ȃ��Ƃ����咣�ł���B���̌����͊�Ƃ͒P�ɐ��Y�v�f�̏W���ł͂Ȃ��C���̉^�c�ɂ���administrative and managerial resources���K�v������ł���B�܂蓊���Ƃ����V�����A�N�e�B�y120�Łz �r�e�B�ɑΉ�����Ƃ��C�g�D�^�c��o�c�͑����ɃX���[�Y�ɑΉ��ł���Ƃ͌���Ȃ��B�����ŐV�����A�C�f�B�A�ɑ��Ē�R���͂��`������邱�Ƃ����蓾��B�V�@������e������ɂ́C��R��r�����邽�߂�extra cost����������B�܂肱��͖{�e�̃��f���œ��������C���x�ɔ�Ⴕ�Ĕ������門�C�̓����팸���邽�߂̃R�X�g�ł���B
�y�����[�Y���ʂ͓����̌��E��p����������Ƃ����咣�ł��邪�C���̂��Ƃ̓��f���̐ݒ肪�قȂ邪�{�_���̘g�g�݂ł����藧���Ƃ�������B
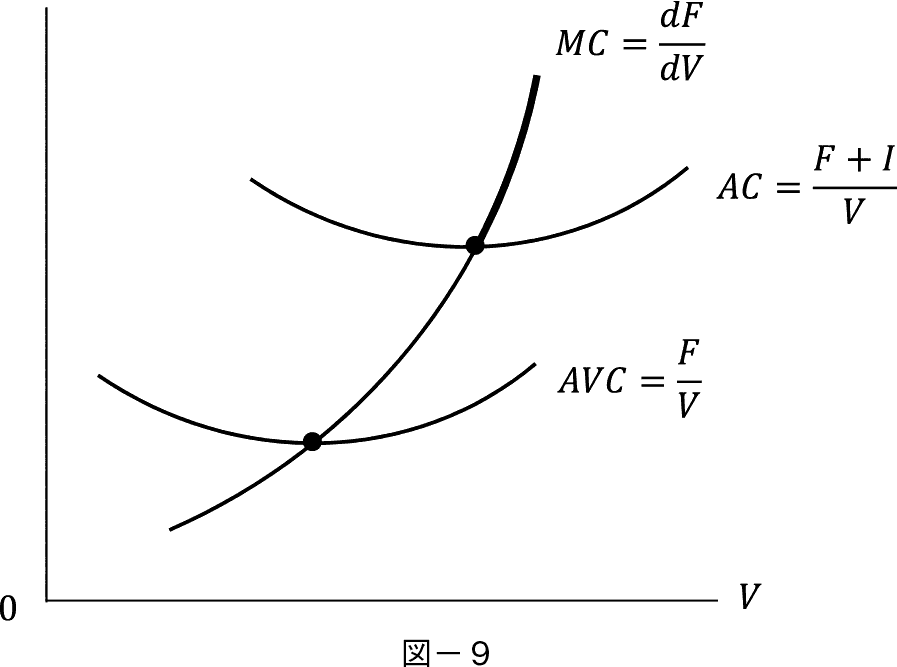
���̒�`�͎��̂悤�ɏ����������Ƃ��ł���B
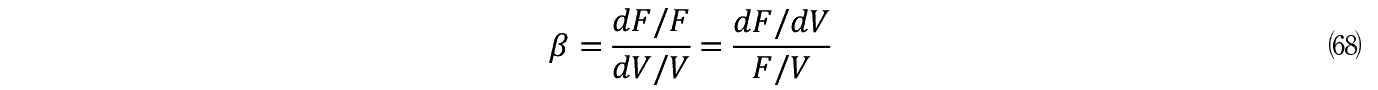
������ F �� V �̊������� F �� V �ɂ��Ẳϔ�p�ƌ��邱�Ƃ��ł���B�����s���� I �͒萔�� V �����R�X�g�ɂȂ�B
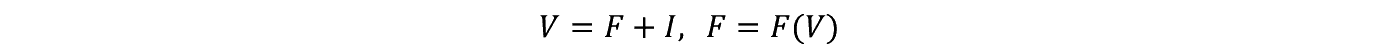
�����ŕ��ϔ�p AC �ƕ��ωϔ�p AVC �͎����Œ�`�ł���B
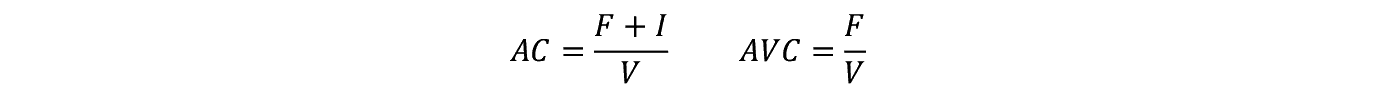
�����Ɍ��E��p MC ��
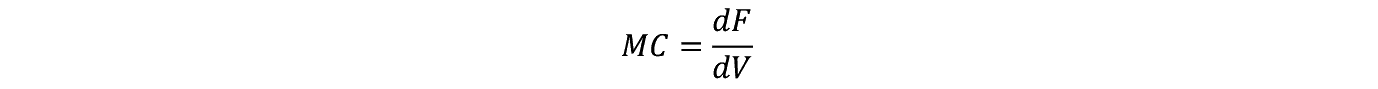
���ϔ�p AC �̕ω������邽�߂� V �Ŕ�������Ǝ�������ɐ��藧�B
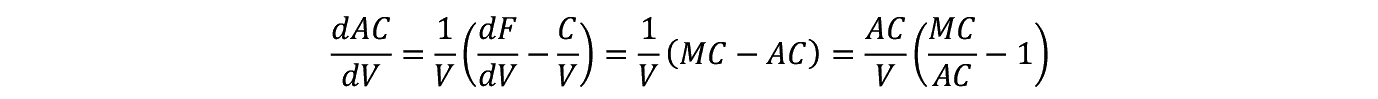
���ϔ�p�� V �ɂ��đ������������
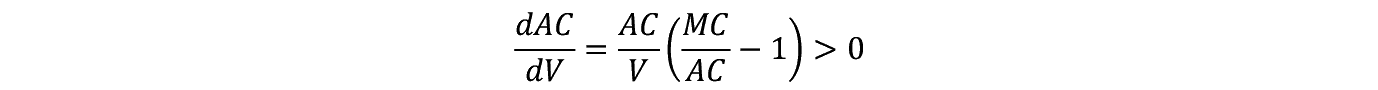
�܂� MC > AC �Ȃ� 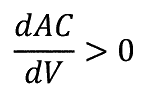 �ł���B
�ł���B
������������������
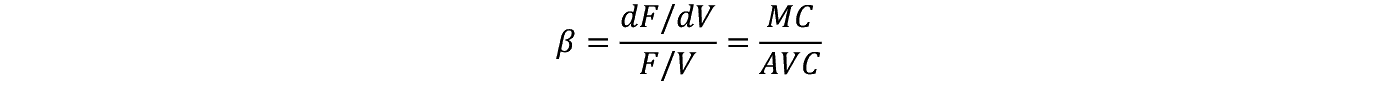
��>�P�̏�����
������ AC ����������ɂ�
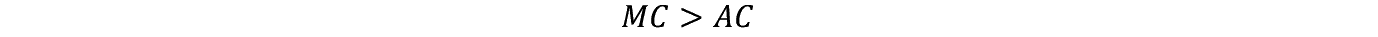
���K�v�ł���B�����Ŏ��}�̂悤�ȊW�����藧�B
�ϔ�p F �i���lj������j�͏������� I ���Ȃ��Ƃ����\�Z������̂ŁC
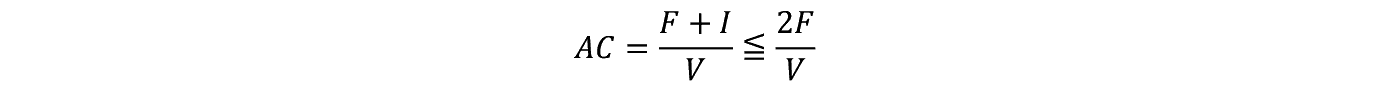
�@��������Q�̂Ƃ���(68)����
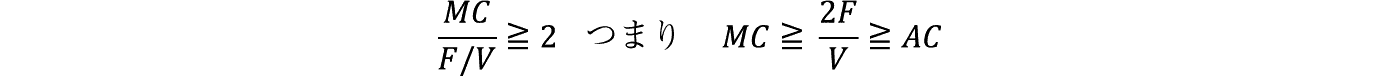
�����藧�B
���Ȃ킿�����Q�Ȃ� MC �͏�� AC ������Ő}�̑����̂悤�ɒ������Ă��Ȃ���Ȃ�Ȃ��B
�F��E�y�����[�Y�Ȑ�10�j �͎��{�������i K / K �F K �͎��{�j�ɑ��Ď��{�P�P�ʓ�����̓����z�i��/ K �F���͓����z�j���������邱�Ƃ��咣���Ă��邪�I�v�V���������ɂ��ē��l�̂��Ƃ����藧�B
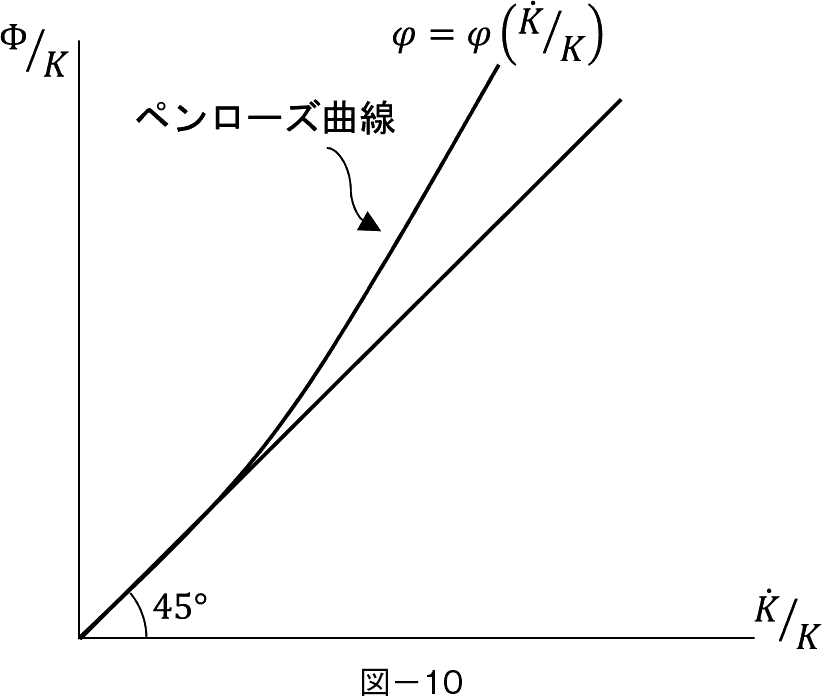
�F�f���ł͕s�m�����͗z�\�I�ɂ͎�������Ă��Ȃ����C�y�����[�Y���ʂƂ͐V�K�����Ƃ����s�m�����ɑ��C�o�c�g�D���Ή��ɋꗶ���u���C�v��������Ƃ������Ƃł���B�܂�y�����[�Y�̊�Ɛ����̃��f���́C�s�m�����ɑΉ�����I�v�V�����Ƃ���F�Ƃ����ϐ����lj��I�ɕK�v�ł��ꂪ�����R�X�g�����������Ƃ������ƂƓ��Ӗ��Ȃ̂ł���B
Abel, A. B �i1983�j �gOptimal Investment under Unceratainty�h Amerian Economic Review 73. pp.229-233.
Black, Fischer and Myron Scholes. �i1973�j. �gThe Pricing of Options and Corporate Liabilities.�h Journal of Political Economy, 81, pp.637-659.
Dixit, Avinash and Robert S.Pindyck. �i1994�j. Investment Under Uncertainty. Princeton University Press.
Hartman, R �i1972�j �gThe effects of price and cort unceratainty on invertment�h Journal of Economic Theory 5. pp.258-266.
Keynes, J.M. �i1936�j. The General Theory of Employment, Interest and Money. Macmillan.
Merton, Robert C. �i1973�j. �gThe Theory of Rational Option Pricing.�h Bell Journal of Economics and Management Science, 4, Spring, pp.141-183.
Richardson, G.B. �i1960�j. Information and Investment. Oxford University Press.
Savage, Leonard J. �i1954�j. The Foundations of Statistics. Dover Books on Mathematics.
Uzawa, Hirofumi. �i1969�j. �gTime Preference and the Penrose Effect in a Two-Class Model of Economic Growth.�h Journal of Politic Economy, 77, No.4, part2. pp.628-652.
Wiener, Norbert, �i1923�j. �gDifferential Space�h Journal of Mathematics and Physics pp.131-173.
�]��m�i1983�j�u�����w�̎��_�v�|���فD
���R�K��i2010�j�u�����̃��A���E�I�v�V�����Y�E���f���F�Z�@�Ǝ���v�����w�@��w�u�o�ό����v��143�� pp.1�`43�D
�{���C�E���� ��i1978�j�u�����������vꠏ��X�D
��i1978�j�u�����������vꠏ��X�D