米国FFR利上げによる米国企業時価総額への
インパクトの分析
-時系列データクラスタリングと次元圧縮による分析-
学習院大学 経済学部 白田由香利
日本経済研究センター 佐倉 環
本稿では,米国連邦準備制度(FRB)が2022年3月以降行った利上げ政策により米国トップ企業100社の株価がどのように変化したかを分析する。変化パターンを解析するため,AI手法による時系列データクラスタリング手法を用いて,その株価変動パターンの類似度指標である距離を計算する。その距離行列は100次元となるので,見やすさのため次元圧縮を行なう。本分析では3種類の異なる次元圧縮手法を実行し,比較検討した。その結果,t-SNEの第1軸が「株価下落を示す指標軸」として最も適していることを発見した。t-SNEの第1軸値によって業種ごとの平均値を求めた結果,エネルギー関連企業はその他の業種に比較して株価下落が少なかったことが判明した。本稿では,米国FFR利上げによる米国企業時価総額へのインパクトの分析として業種比較を行うことを事例として,株価変動パターンの類似度計算から,分析意図に適合した主成分軸を発見するAI的手法について述べる。
米国FRB(Federal Reserve Board)がインフレを抑制するため,短期金利であるFFレート(Federal Funds Rate)の利上げを2022年3月のFOMC(連邦公開市場委員会:米国の金融政策を決定する会合)で決定し,そこから連続した利上げが開始された[1][2]。これは経済活動の過熱を抑制するために行っているので,結果,株価は下落の方向に動く。我々はこの利上げのインパクトを,経営学的視点から分析したい。つまり消費者物価指数や失業率などの経済的視点からの指標ではなく,経営学的に分析する。例えば,利上げによって影響を受ける業種はどこであるか,また,その影響の度合いの時系列変化等を距離として測る。用いるデータは,株価ではなく,米国の売上高TOP 100の企業の時価総額(株価×発行株式数)を用いる。分析では,時価総額の下落幅の大きい(小さい)業種,企業を調べる。そのためには,本分析では,株価下落の度合いを示す軸を抽出したい。手順としては,変動パターンの間に類似度である距離を定義すること,その距離を企業間で計算し距離行列を計算すること,その距離行列を次元圧縮して,指標軸を抽出することが重要となる。本分析では,3種類の次元圧縮手法を比較検【38頁】 討して,その中から分析意図に最も合致する主成分軸を抽出した。こうした,意図する次元圧縮軸を抽出するアルゴリズムは多種多様に存在するので,分析者にとって選択が難しいが,本稿では具体的データを使って,主成分軸の抽出成功事例を示す。
第2節では,分析に用いたデータを説明する。第3節では分析手法を説明する。第4節では,次元圧縮の結果を示す。第5節は,株価時系列データクラスタリング結果を経営的視点から考察する。最終節はまとめである。
データについて説明する。ここでは,米国企業で売上高が2022/9/27時点でTOP100の企業の,2022年3月1日から9月27日までの時価総額を用いた。データはビューロー・ヴァン・ダイク社の企業データベースORBISから検索した。
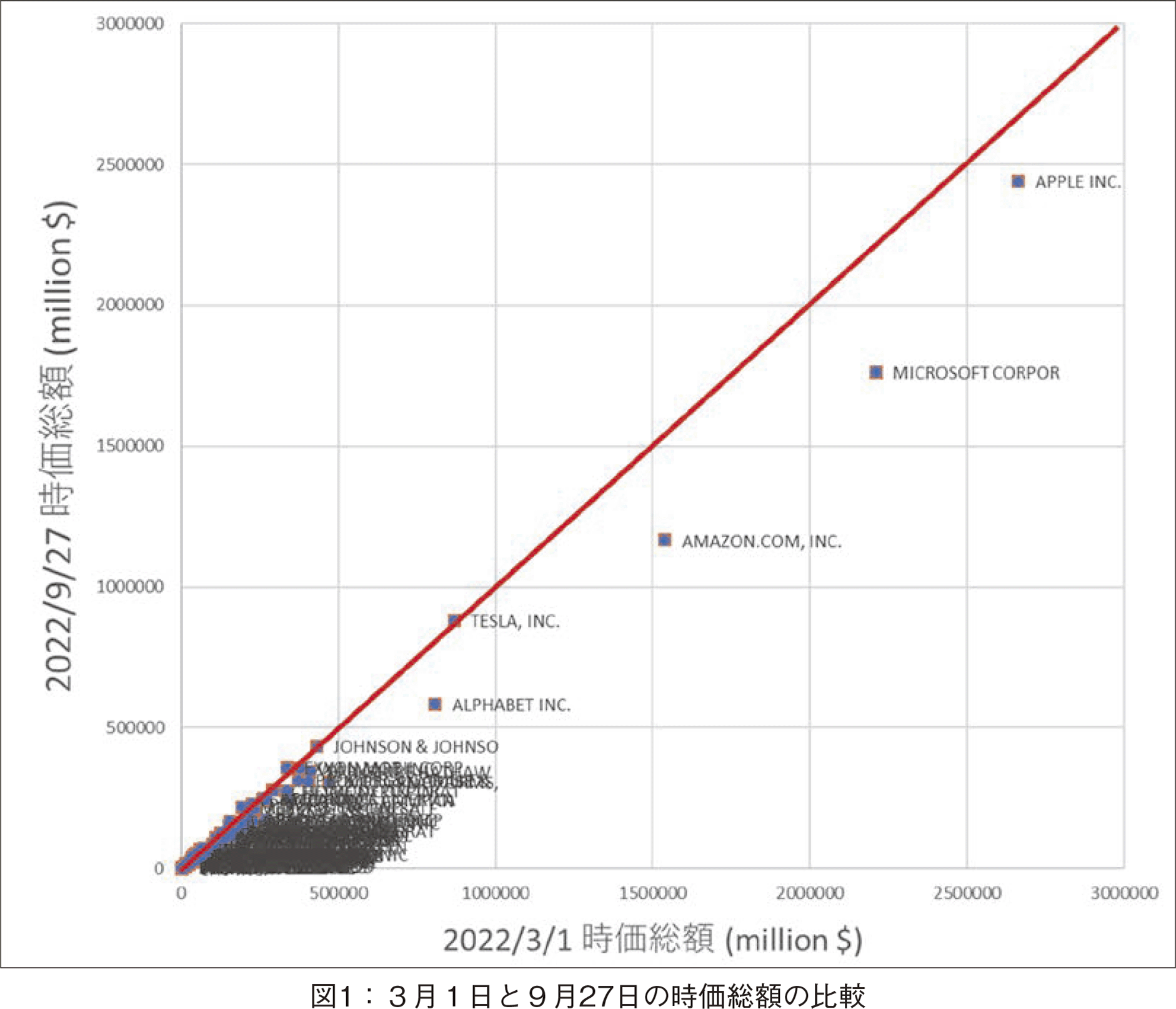
初めに全体的な変動のようすを把握するため,図1に3月1日と9月27日の時価総額の比較を示した。赤の斜線は45度の傾きの直線である。株価が暴落し,時価総額が下落したとしても,9月27日時点で3月1日時点の状態に回復していれば,この斜線よりも上側にいく。当該7か月を経過した後,時価総額に変化がなければ,45度の赤い直線上に乗る。その線上から下側に位置する企業が時価総額を下げた企業である。テック・ジャイアント企業を中心に見ていくと,時価総額の規模の大きい順に,アップル,マイクロソフト,アマゾン,アルファベットが時価総額を下落させていることが分かる。テスラはほぼ直線上に乗っている。両日の下落率では,アマゾンが最大である。メタは左側の集団中に位置するため図1では判別できないが,メタの時価総額も下落している。このように米国のテック・ジャイアント企業は軒並み時価総額を下落させた。
こうした初期値と7か月後の値だけでは,変動パターンの詳細な違いは分析できない。そこで,時系列クラスタリングを用いて,変動パターンとしての類似度を測る。より良いポートフォリオ作成には,一般にAI手法によるクラスタリングが必須となる。Pradoが階層型リスクパリティ(HRP)法[3],[4],[5]を開発してから,クラスタリング手法は広く普及し,各種の階層型クラスタリング手法[6],[7],[8][9]がその改良版として開発されてきた。
本節では用いた分析手法を説明する。主成分軸を抽出するためには,初めに企業株価パターン間の距離を定義する[10],[11],[12]。次元圧縮をするだけであれば,距離行列だけで十分でありクラスタリングは必要ないが,類似パターンのクラスターを求めることも分析上必要なので,クラスタリングを行う。以下では,クラスタリング手法,ついで3種類の次元圧縮法について述べる。
本節では分析で用いたクラスタリング手法について説明する。株価及び時価総額の変動パターンのクラスタリングは時系列データクラスタリング手法を用いる。時系列データクラスタリングで広く使われている手法として,k-Shape法[13],HRP(Hierarchical Risk Parity)法[14]などがあるが,いずれも入力データの標準化を必要とする手法であり,株価の変動のリスク(標準偏差)情報を除去してしまう。データの分散情報はリスク情報として重要であり除去すべきではない[15]。そこで我々は分散を含めて変動パターンをクラスタリングするAmplitude-based clustering手法[16][12]を用いる。Amplitude-based clustering法の距離は,ユークリッド距離をベースとする距離である。Amplitude-based clustering法では入力データに対してデータ標準化は行わない。Amplitude-based clusteringのクラスタリングアルゴリズムは階層型クラスタリングである。クラスタリングの後,准対角化を行い,距離行列の対角線上に距離の近いデータができるだけ近く配置されるように,データの順番を入れ替える。これを准対角化と呼ぶ。Amplitude-based clusteringによる株価の分析事例として[17][18][19][20]がある。その用法の解説としてはDEIM2013のチュートリアルのビデオも参照して頂きたい[10]。
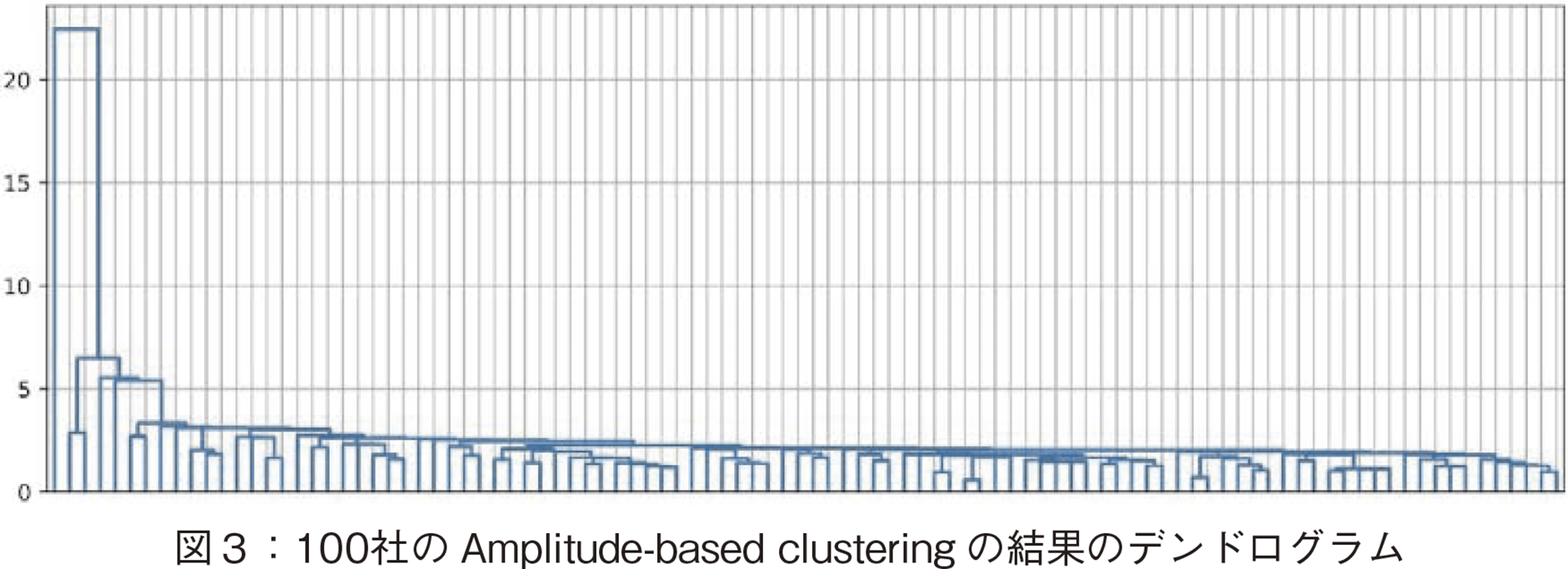

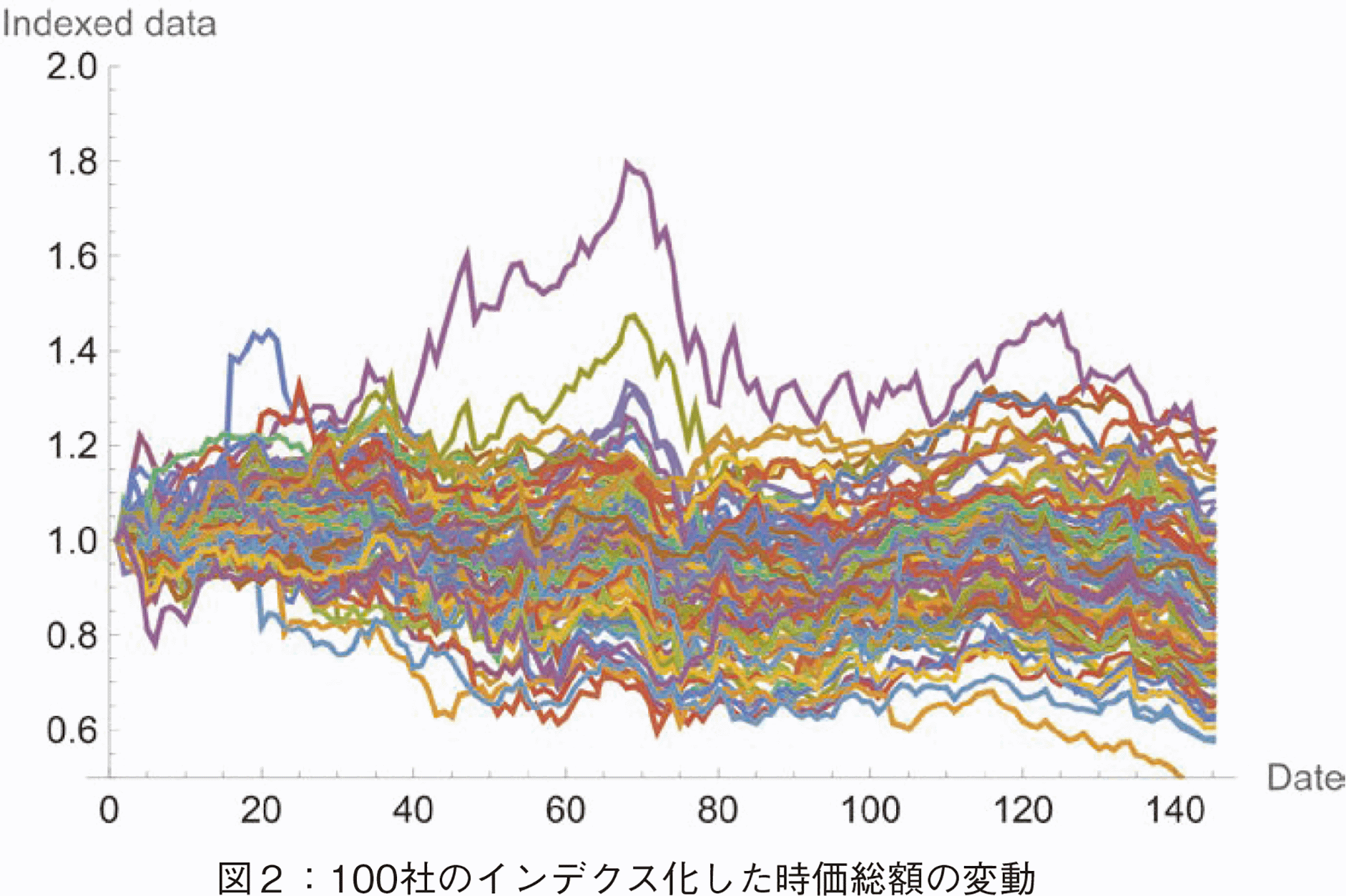
本稿の分析のクラスタリングについて説明する。データは,そのままの時価総額データ値では図1に示すように企業の規模によりスケールが異なる。株価回復力などの比較のため,初期値である2022/3/1の時価総額値を1としてインデクス化したデータを用いる(図2参照)。このインデクス化により,その企業が3/1のデータを基点としてどのように変動したかが表現可能となる。このインデクス化はデータの標準化とは異なる。インデクス化しても,変動により平均値および標準偏差は異なる。その標準偏差の違いを判別するために,Amplitude-based clustering法を用いた。本分析のクラスタリング結果を図3,図4に示した。いずれも准対角化後のデンドログラムと距離行列である。図3の縦軸は企業株価パターン間の距離を表す。
時系列データクラスタリングの結果,生成された距離行列を次元圧縮する。本分析では100次元を2次元に圧縮する。次元圧縮の手法としては,(1)主成分分析(PCA),(2)t-SNE,(3)UMAPの順で普及してきた。PCAは数学的解であり,分散最大化問題として解析的に解いた解である[21]。クラスタリング結果の100次元の距離行列(図4)を入力としてPCAをする,という方法も考えられるが,本分析では,元のインデクスデータを入力として特異値分解(SVD)を用いた。特異値分解もPCA同様に数学的解であり,t-SNEのような近似解ではない。株価データに対して特異値分解を行う数学解説については[22]を参照して頂きたい。
2,3番目の手法であるt-SNE[23],[24]とUMAP[25],[26]は,いずれも高次元空間上で距離の近い点が,次元圧縮後の例えば2次元空間においても近いように配置する(次元圧縮する)近似的解法である。 t-SNEでは2点の類似度を,ユークリッド距離から計算される条件付き確率として表現するが,一般にデータが高次元になると,特定の点から等距離に位置する点が増加するので,密度を低減するために,低次元空間での類似度の表現に正規分布よりも裾野の広い自由度1のt分布を用いる[27]。
UMAPは,代数トポロジーとリーマン幾何学の理論に基づき,多次元空間の距離の次元圧縮問題を,幾何学的に扱いやすいリーマン多様体上の最適化問題として解く。昨今,機械学習においてはユークリッド空間の手法からリーマン多様体上の手法への一般化が主流となっている[28]。リーマン多様体を使った最適化手法については[29],[30]を参照して頂きたい。t-SNEはユークリッド距離をもとに次元圧縮を行い,UMAPはリーマン多様体上での距離をもとに次元圧縮を行っている。後発したUMAPの方がリーマン多様体上の距離を使うので,性能がよいと言われているので,本分析ではUMAPを用いた[25],[26]。しかし結果的には,今回の分析では,UMAPよりもt-SNEが抽出した第1軸が最も我々の分析意図に合っていた。詳細は次節で述べる。
本節では,100社のクラスタリング結果を解釈する。図3にデンドログラム,図4に距離行列のヒートマップを示した。ヒートマップでは白い色の方が,距離が近いことを示す。図3,4とも,准対角化後の順番で並べている。デンドログラムの左端の企業が,ヒートマップの1番上の企業である。デンドログラムから分かることは,左端の1社が他の企業の変動と大きく異なる変動をもつこと,殆どの企業が狭い距離範囲内に存在していることである。図2に100社のデータの折れ線グラフを示したが,上側に突出している紫色の1社がこの左端の企業である。この会社はバレロ・エナジー(Valero Energy Corporation(VLO))で,石油精製・販売会社である。当該期間に多くの企業が株価を下落させたが,エネルギー関連企業は堅調であったことから,バレロ・エナジーが高いパフォーマンスを示したことは納得できる。
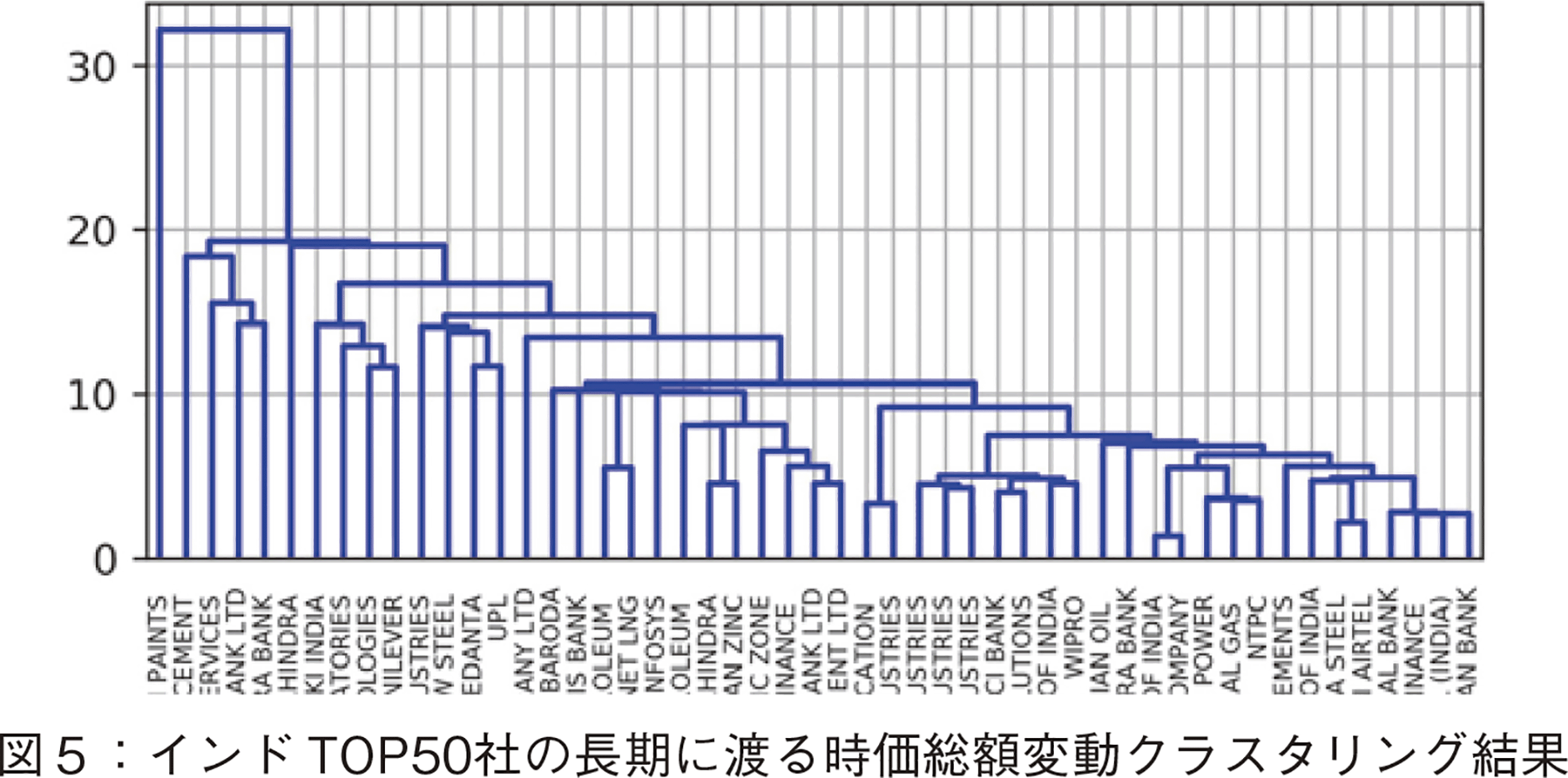
今回の時価総額パターン変動は単調ではない。既存研究で,インドの長期にわたる時価総額変動分析で同様の手法でクラスタリングを行った結果があるが,全体傾向が成長であったので,距離の分散が大きく差異が顕著であった[17]。図5にその結果のデンドログラムを示す。【43頁】 縦軸が距離である。図3の今回の分析のデンドログラムに比較して,距離の分散が全体的に大きいことが分かる。今回のデータは,殆どの会社の間で距離の分散が小さく,その中で,変動パターンが複雑に変化しているので,距離レベルによって分類していくことが難しかった。そこでまず次元圧縮を行うこととした。次元圧縮による抽出軸は,データ間の差異を見るための主要成分を抽出してくれるからである。
本節では,3種類の次元圧縮で2次元に圧縮した結果を比較検討する。図6に3手法による結果を示す。
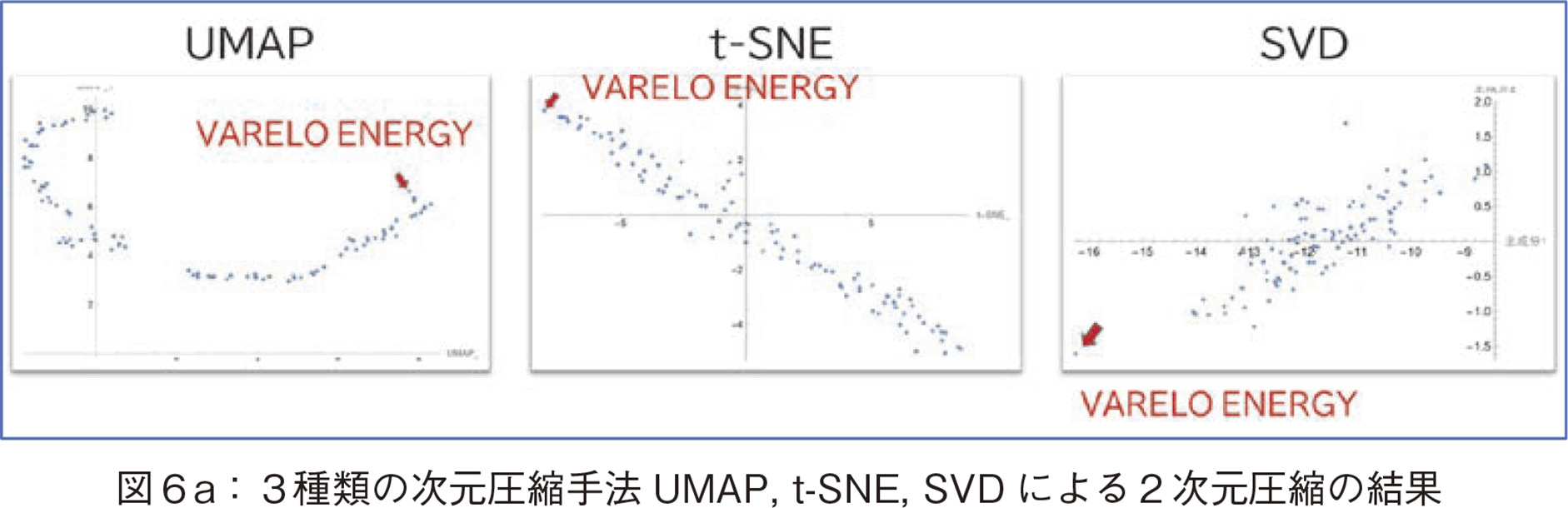
図6の各図で第1軸をx軸,第2軸をy軸で示した。また,赤矢印でバレロ・エナジーを示した。t-SNEの結果にテック・ジャイアント企業とバレロ・エナジー社をマークして示した。
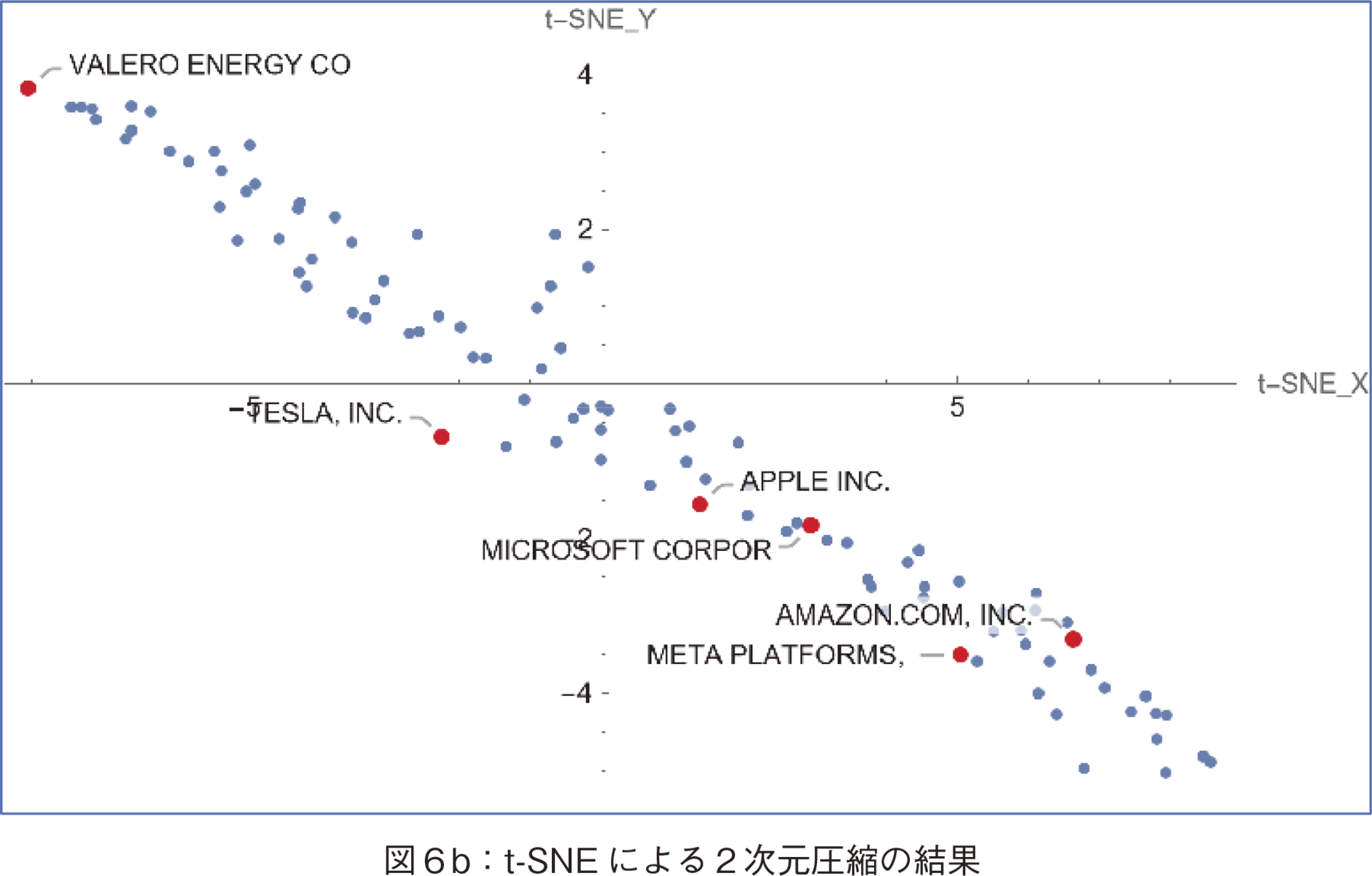
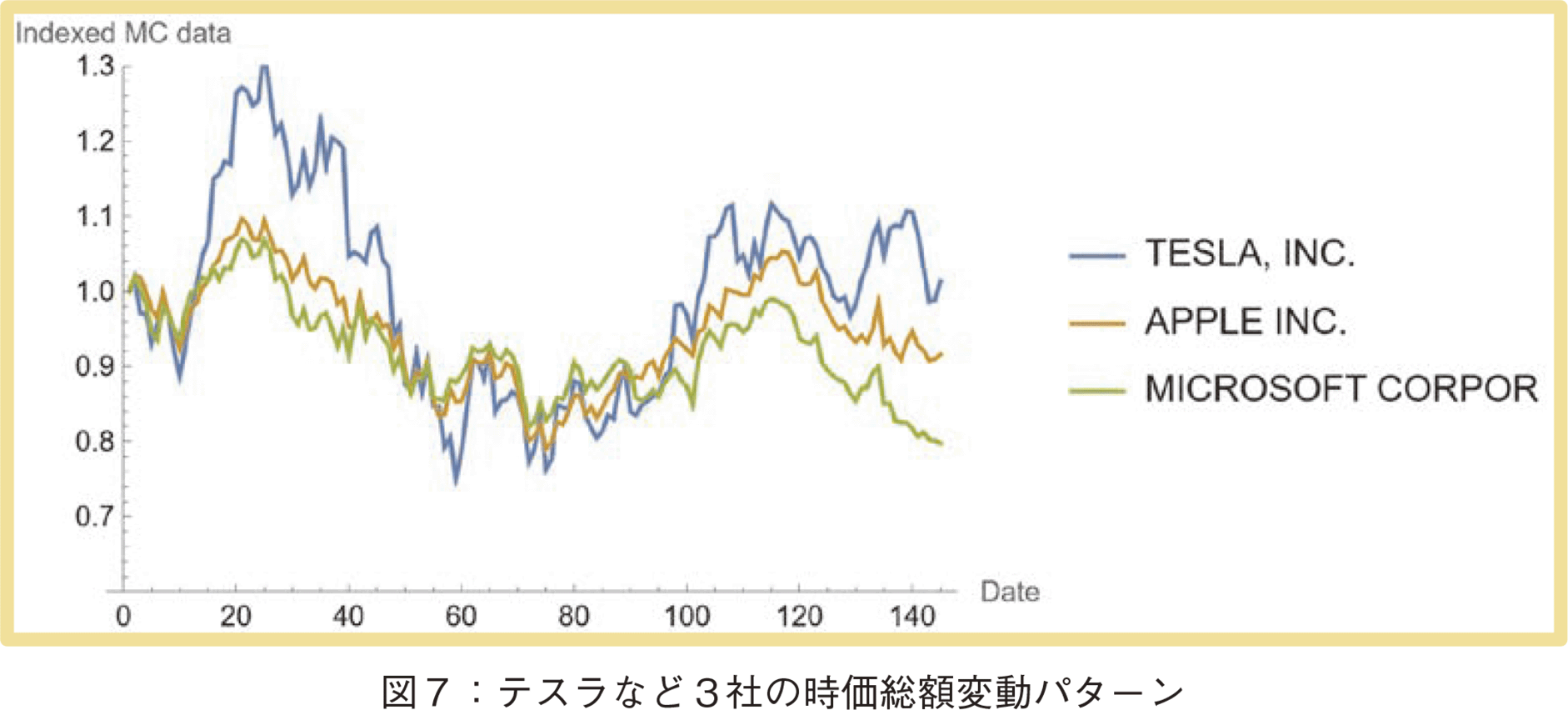
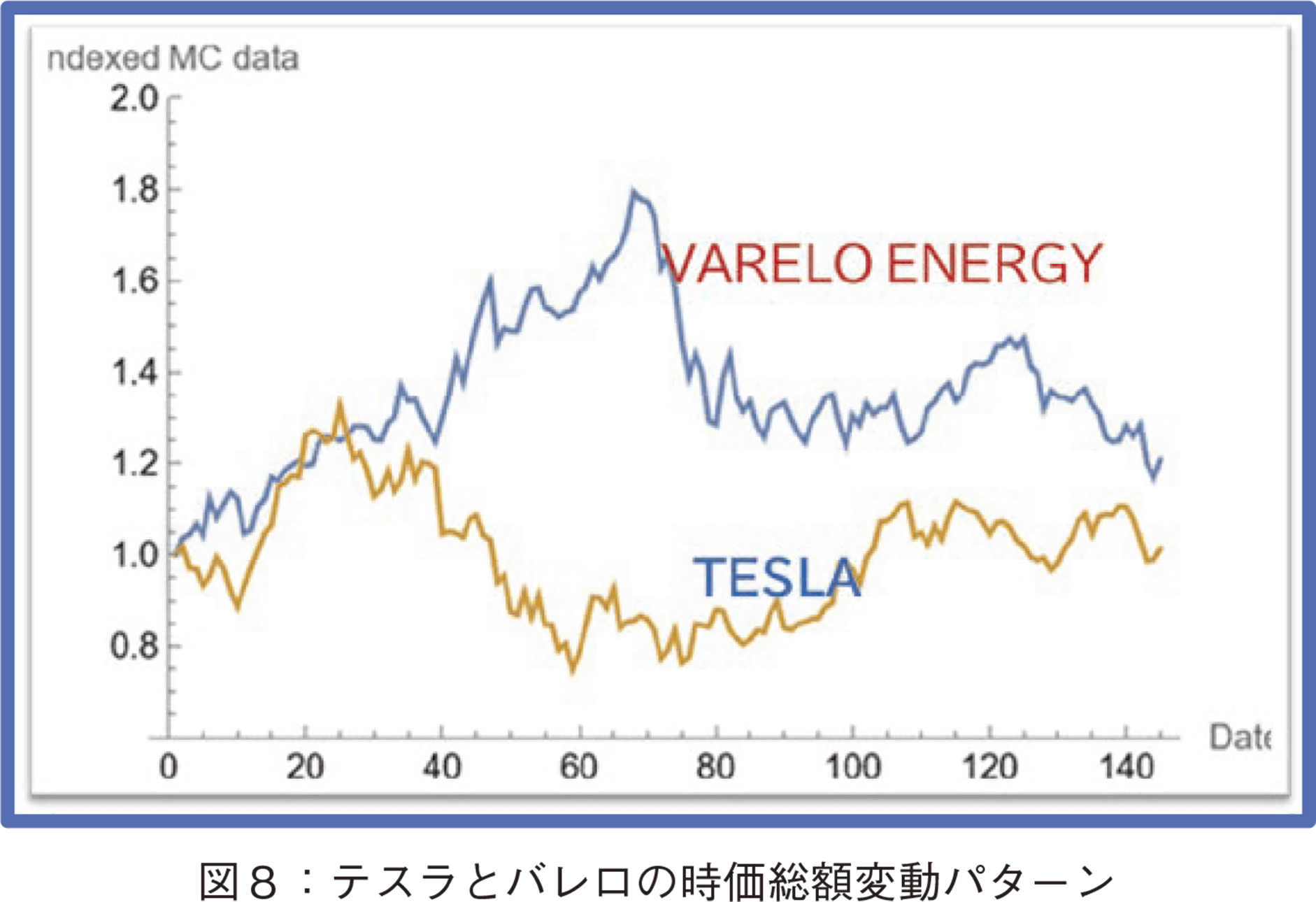
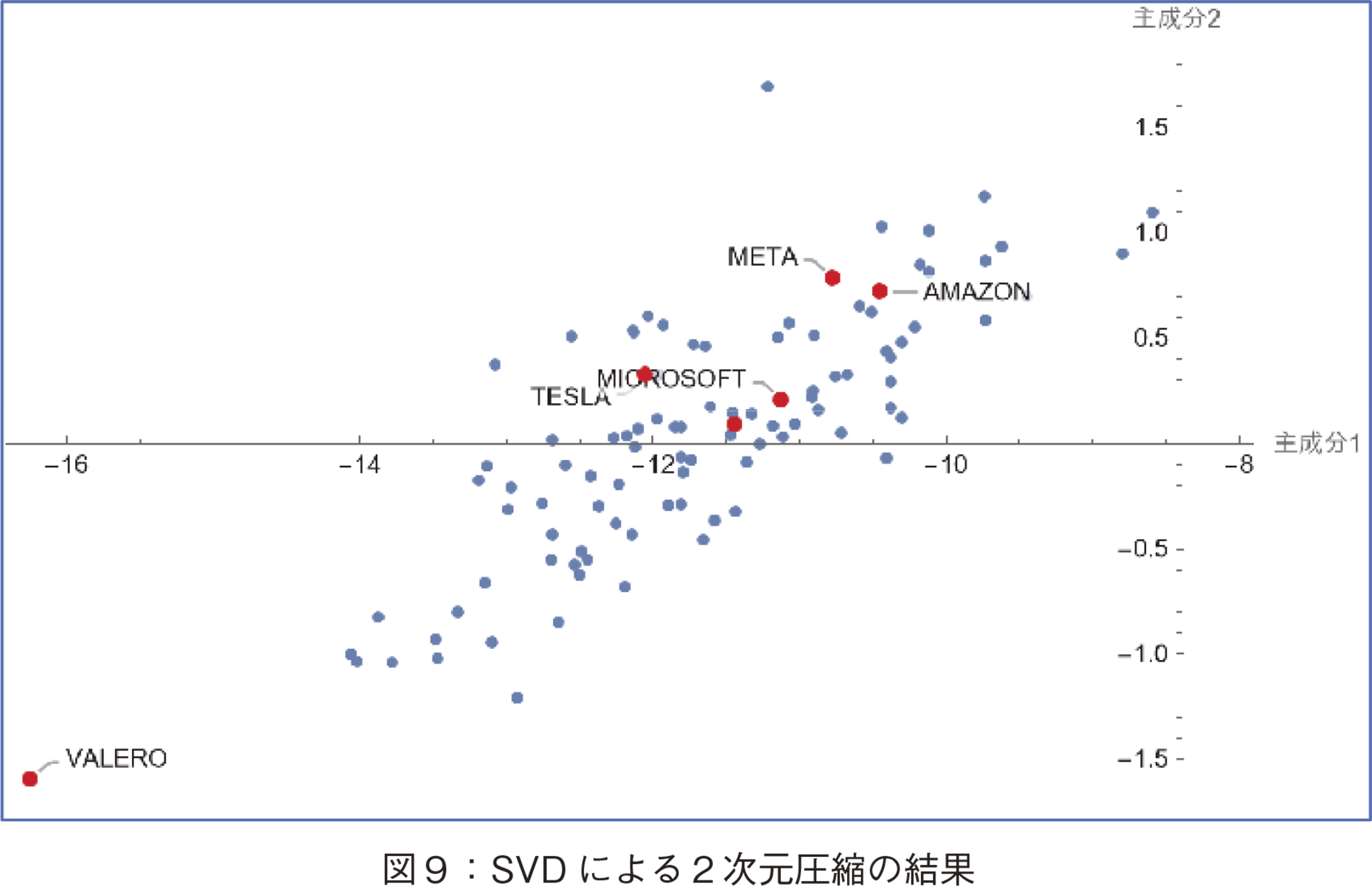
図7と図8にテスラなどの企業の時価総額変動パターンの比較を示した。この動きと図6のt-SNEによる2次元圧縮の結果を考察すると,t-SNEの第1軸(x軸)は株下落のレベルの指標と解釈可能である。このx値が大きくなるほど株価下落傾向が高い。高いパフォーマンスのバレロ社が最小x値を取っていることも,この解釈に肯定的である。次に図9にSVDの次元圧縮の結果を示した。同様に代表的企業をマークすると,t-SNEのx軸とSVDのx軸(第1主成分軸)の値の順番は同じであり,SVDのx軸も株下落のレベルの指標と解釈可能である。
次にUMAPによる次元圧縮結果を見る(図10参照)。
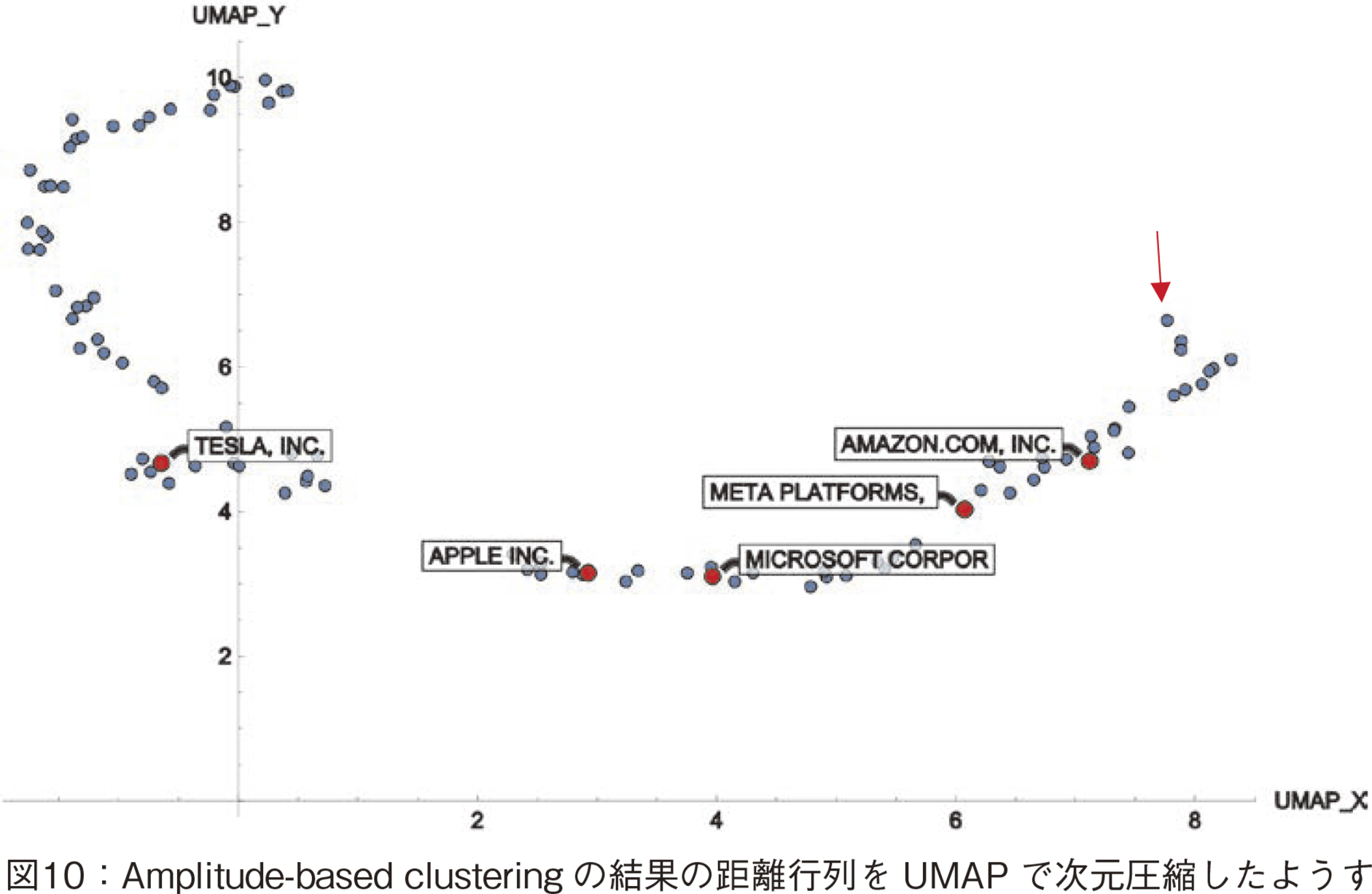
UMAPによって生成された第1主成分に相当する軸をUMAP_Xと呼ぶ。図10中で,テック・ジャイアンツの5社を赤点で示した。この5社の並び順はt-SNEのx値と同じであるが,赤矢印でマークしたバレロ社がx軸の右端にあることから,x軸は我々の分析意図と異なる主成分軸であることが分かる。結論からいうと,UMAP_Xは,株価下落の指標軸としては不適である。
後発のUMAPはリーマン多様体上での距離の近さを測るので性能がよい,と考えられやすいが,この事例のように人間の分析意図とは異なる距離空間にマッピングすることがある。換言すると,人間の意図と同じ主成分軸を第1軸として取ってくれるという理由も保証もない。株の変動パターンに限らず,一般に次元圧縮手法を用いるときは,UMAP,t-SNE,PCA(あるいはSVD)などの複数手法による比較を行うことが重要である。この分析において,分析者の意図にあった指標はt-SNEのx軸であると判断した。SVDのx軸もよいが,両者を比較した場合,x軸の分散の値に関して,t-SNEのほうが大きいからである。次節では,t-SNEのx軸を指標軸として利用した分析を行う。
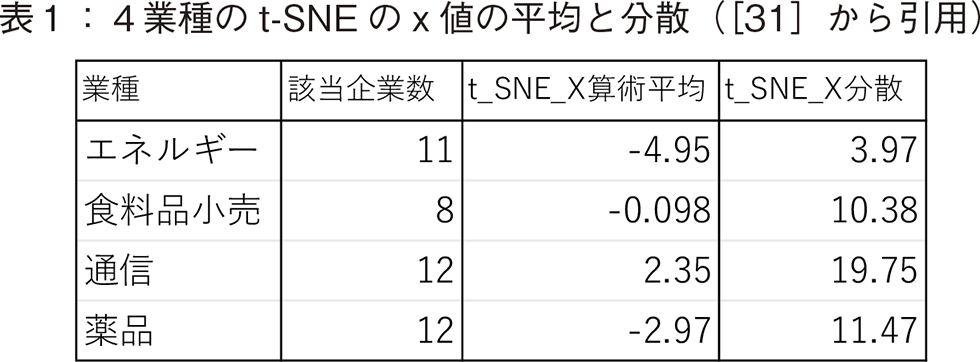
本節では,t-SNEのx軸を株価下落指標軸として用いることで,企業の業種の違いを分析する。FRBの利上げの影響を受けにくい業種として,エネルギーなどの4つの業種について,そのt-SNEのx軸値の平均と分散を計算した結果を表1に示す([31]から引用)。高畠らが示したように,エネルギー関連企業が最もx値が小さく,株価下落が小さいようすが分かる。エ【47頁】 ネルギー関連企業のx値の分散も小さく,企業間の変動も小さいことが分かる。エネルギー関連企業が業界全体として安定して高いパフォーマンスを出した,と解釈できる。ついで,薬品業界,食料品小売業界において株価下落が少なかったことが分かる。以上の分析を総括すると,最も株価下落レベルが低かった業種はエネルギー企業であり,それに続き薬品企業及び,食料品小売企業の株価下落レベルが低かった。通信企業については,この3業種に比較すると,株価下落レベルが小さいとは言いづらい結果となった。ただし,これは米国のこの時期のTOP100の企業に関する分析結果に基づくものであり,業種と金利上昇との普遍的な関係を言うにはさらなる検証が必要となるであろう。
本稿では,米国連邦準備制度(FRB)が2022年3月以降行った利上げ政策により米国トップ企業100社の株価がどのように変化したかを分析した。使用するデータは時価総額で,期間は2022年3月1日から同年9月27日である。3月1日のデータを1としてインデクス化した値,時価総額インデクスの変動パターンの類似度をAI手法による時系列データクラスタリング手法を用いて求めた。クラスタリング手法としてAmplitude-based clustering手法を用いて,標準化なしのデータの分散の違いを観察した。クラスタリングの結果の距離行列は次元サイズが大きく解釈が困難であるため,次元圧縮手法により2次元に圧縮をかけた。株価変動パターンの時系列変化は複雑形状であるため,適切な次元圧縮手法を選択することが必要となる。本分析では,UMAP,t-SNE,SVDの3種類を用いた。結果としてはt-SNEの第1主成分時軸が,我々の意図「株価下落のレベルを表す指標」に最も近いと判断した。後発のUMAPはリーマン多様体を用いる効率的手法であるが,本分析では,我々の意図とは異なる距離空間に次元圧縮したと考えられる。次に t-SNEの第1軸値によって業種ごとの平均値を求めた結果,エネルギー関連企業はその他の業種に比較して株価下落が少なかったことが判明した。本稿では,米国FFR利上げにより大多数の企業が大きな打撃を受けたが,エネルギー関連企業は影響が少なかったことが分かった。ついで,薬品企業及び,食料品小売企業の株価下落レベルが低かった。
本稿では,2022年のFRB利上げの時期の時価総額データを用いて,株価変動パターンの類似度計算から,分析意図に適合した主成分軸を発見するAI的手法について説明した。クラスタリングの手法,次元圧縮手法は各種アルゴリズムがあり,選択が困難であるが,少なくとも本稿で示した組み合わせにより,分析可能であることを示すことができた。
本研究は部分的に,学習院大学計算機センター2023年度特別プロジェクト,学習院大学GEMプロジェクト2023年度の助成によるものである。
[1] F. R. Board, "Transcript of Chair Powell’s Press Conference," 2022. [Online]. Available: https://www.federalreserve.gov/mediacenter/files/
[2] B. o. G. o. F. R. System, "FOMC Press Conference Live Video," 2022. [Online]. Available: https://www.federalreserve.gov/live-broadcast.htm
[3] M. L. De Prado, Advances in financial machine learning John Wiley & Sons, 2018.
[4] M. M. L. de Prado, Machine learning for asset managers Cambridge University Press, 2020.
[5] M. L. d. Prado, "Keynote speech : Advances in Financial Machine Learning," ACM ICAIF (AI in Finance), online, 2020.
[6] H. Lohre, C. Rother, and K. A. Schäfer, "Hierarchical Risk Parity: Accounting for Tail Dependencies in Multi‐asset Multi‐factor Allocations," Machine Learning for Asset Management: New Developments and Financial Applications, pp. 329-368, 2020.
[7] M. Molyboga, "A modified hierarchical risk parity framework for portfolio management," The journal of financial data science, vol. 2, no. 3, pp. 128-139, 2020.
[8] L. Cao, "Ai in finance: challenges, techniques, and opportunities," ACM Computing Surveys (CSUR), vol. 55, no. 3, pp. 1-38, 2022.
[9] J. Pfitzinger and N. Katzke, "A constrained hierarchical risk parity algorithm with cluster-based capital allocation," Stellenbosch University, Department of Economics, 2019.
[10] 白田由香利,“チュートリアルT2:株価分析のための時系列データクラスタリング入門,”DEIM2023 電子情報通信学会,岐阜長良川国際会議場,2023.
[11] A. A. Patel, Hands-on unsupervised learning using Python: how to build applied machine learning solutions from unlabeled data O'Reilly Media, 2019.
[12] 白田由香利,“株価変動パターンの機械学習クラスタリング,”日本経営数学会第44回(通算64回)研究大会 日本経営数学会,東京,pp. pp. 4-7, 2022.
[13] J. Paparrizos and L. Gravano, "k-shape: Efficient and accurate clustering of time series," Proceedings of the 2015 ACM SIGMOD international conference on management of data, pp. 1855-1870, 2015.
[14] D. P. M. Lopez, "Building diversified portfolios that outperform out of sample," The Journal of Portfolio Management, vol. 42, no. 4, pp. 59-69, 2016.
[15] S. Matsuhashi and Y. Shirota, "Note for Shape-Based Clustering in Stock Prices," Proc. of IIAI International Congress on Advanced Applied Informatics 2022, 3-7 July, 2012, Kanazawa, Japan, pp. 373-377, 2022.
[16] Y. Shirota and B. Chakraborty, "Amplitude-Based Time Series Data Clustering Method," Gakushuin Economics Papers, vol. 59, no. 2, pp. 127-140, 2022.
[17] Y. Shirota, B. Chakraborty, B. Sreekanth, and H. Yoshiura, "Ambidextrous Time Series Data Clustering with Amplitude- based and Shape-based Distances - Case Study of Indian Companies’ Growth Pattern of Aggregate Market Values -," The Economic Perspective on Artificial Intelligence (EPEAI) International 【49頁】 Conference Ruhr West University of Applied Sciences, Dusseldorf and online, pp. in printing, 2023.
[18] S. Matsuhashi and Y. Shirota, "Resilience Evaluation of Automakers After 2008 Financial Crisis by UMAP," International Journal of Machine Learning, vol. 13, no. 3, pp. 125-130 2023.
[19] H. Ito, A. Murakami, N. Dutta, Y. Shirota, and B. Chakraborty, "Clustering of ETF Data for Portfolio Selection during Early Period of Corona Virus Outbreak," Gakushuin Journal of Economics, vol. 58, no. 1, pp. 99-114, 2021.
[20] 白田由香利,佐倉環,and B. Chakraborty, “世界自動車製造業2014年度株価成長の時系列分析,”学習院経済論集,vol. 59, no. 2, pp. 141-160, 2022.
[21] C. M. Bishop and N. M. Nasrabadi, Pattern recognition and machine learning Springer, 2006.
[22] Y. Shirota and B. Chakraborty, "Visual Explanation of Eigenvalues and Math Process in Latent Semantic Analysis," Information Engineering Express, Information Engineering Express, vol. 2, no. 1, pp. 87-96, 2016.
[23] L. Van der Maaten and G. Hinton, "Visualizing data using t-SNE," Journal of machine learning research, vol. 9, no. 11, 2008.
[24] L. Van Der Maaten, "Accelerating t-SNE using tree-based algorithms," The journal of machine learning research, vol. 15, no. 1, pp. 3221-3245, 2014.
[25] L. McInnes, J. Healy, and J. Melville, "Umap: Uniform manifold approximation and projection for dimension reduction," arXiv preprint arXiv:1802.03426, 2018.
[26] A. Coenen and A. Pearce, "Understanding umap," Google PAIR, 2019.
[27] 株式会社ブレインパッド,“高次元データの可視化を目的とした次元削減手法を紹介,” 2022. [Online]. Available: https://blog.brainpad.co.jp/entry/2022/03/09/160000
[28] 笠裕之,“曲がった空間上の最適化,” 2022. [Online]. Available: https://www.fse.sci.waseda.ac.jp/20200415-kasai/
[29] 佐藤寛之 and 笠井裕之,“リーマン多様体上の最適化の基本と最新動向,”システム/制御/情報,vol. 62, no. 1, pp. 21-27, 2018.
[30] H. Sato, Riemannian optimization and its applications Springer, 2021.
[31] 高畠早紀 and 白田由香利,“利上げによる米国企業時価総額への影響分析 〜 Amplitude-based clusteringによる時系列分析 〜,”電子情報通信学会技術研究報告,pp. 1-5, 2023.