Structural Analysis of India SDG Scores
−Time series data analysis with clustering and triple correlation coefficients−
Yukari Shirota
(Department of Management, Faculty of Economics, Gakushuin University, Japan)
Basabi Chakraborty
(Iwate Prefectural University, Iwate, Japan
Madanapalle Institute of Technologies and Science, AP, India)
Abstract
In this work, the structural relationship among 17 SDG goals have been analyzed using India's state-specific SDG scores. The objective of this study is to find out the area where the government should invest in order to improve the overall SDG’s achievement efficiently. We have used popular hierarchical clustering and the triple correlation coefficient proposed and developed by the authors. Most multivariate data analysis methods in current statistics are based on covariance or correlation coefficient. Covariance and correlation coefficients deal only with the relationship between two variables and do not simultaneously calculate relationship among more than two variables. In this paper, we propose a triple correlation coefficient that shows the relationship among three variables at once and analyze the structure among SDGs achievements using the triple correlation coefficient. The analysis reveals that the fourth SDG, improving the level of education, has the broadest and strongest relationship with the other goals.
Keywords: India, SDG attainment, effectiveness of education, triple correlation coefficient, hierarchical clustering
This research aims to examine India's state-specific SDGs[1] achievements and analyze the relationship among the goals based on state-specific SDG [1] data in India. In collaboration with the Madanapalle Institute of Technology, India [2], [3], [4], our further aim of research is to explore the specific goals which should be focused more in order to improve the overall achievement efficiently, the higher the score, the achievement of SDG is considered as the better. For example, SDG #3 is the achievement of health and well-being, and we plan to determine the required direction of investments in order to improve the achievement score of SDG #3 [4]. The SDG data, published according to 【248頁】 different states in India, is collected from the website of NITI Aayog, a public policy think tank of the Indian government [5]. Scores are on a 100-point scale, with higher scores indicating higher achievement. We consider data of each state as a multivariable data with various SDG goal scores as its attribute variables, and calculate correlation coefficients and distances between the variables. In the next section, we describe the analysis methodology in detail. Section 3 presents the results of analysis for the 2020 data, and Sections 4 and 5 present the results of 2019 and 2018 data respectively followed by the summary of analysis in section 6. In Section 7, the related works on triple correlation coefficient are surveyed. Section 8 presents the discussion and the final conclusion.
2. Triple correlation coefficient
This section describes the triple correlation coefficient proposed by the authors in[6].
The concept of covariance is an essential measure of data characterization in multivariate analysis methods[7], [8], [9]. For data analysis, the first step is to visualize the data to have an overview of it and Principal component analysis (PCA) is often used for this purpose. Principal components are obtained by determining the eigenvalues and eigenvectors of the variance-covariance matrix[10]. SEM (Structural Equation Modeling)[11], [12] mathematically encompasses existing models such as factor analysis, analysis of variance, and path analysis, but their core idea is covariance. The correlation coefficient is a standardized measure of covariance[13]. Thus, it is no exaggeration to say that current multivariate analysis methods are built based on the concept of covariance. However, covariance deals only with relationship between two variables and does not simultaneously calculate relationship among more than two variables. In this paper, the triple correlation coefficient, which indicates the relationship among three variables, is used.
In a multivariate analysis, let us suppose that three variables could be called a triplet among many variables. An example is the structure among SDG scores shown in Figure 1. Figure 1 is a dendrogram resulting from a hierarchical clustering of the 17 scores for a particular state in India in 2020. The variables are divided into clusters according to their proximity. The horizontal axis of the dendrogram represents the distance between two clusters. The stronger the correlation, the smaller the distance. Here, the distance is defined using the correlation coefficient r_xy, x and y being two clusters. For more details, see.[6] .
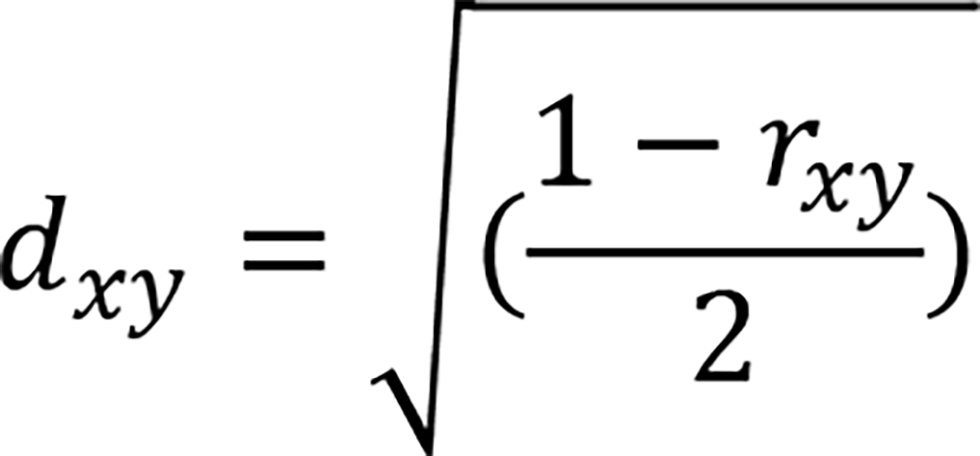
Since the data in this case study is based on Indian state-by-state data, a scatter plot between SDG#i and SDG#j shows each Indian state as a single point. The higher the correlation coefficient between variables, the closer the distance between the two variables. In Figure 1, a certain threshold is set for the distance, and SDG variables with a distance below the threshold are considered being in one cluster and colored. Changing the threshold value will change the components of the clusters (increasing the threshold results in merging of clusters while decreasing the threshold results in splitting of a cluster).
【249頁】Of the 17 SDG scores, SDG #1 (poverty) and SDG #2 (hunger) are close and form a cluster. The figure also shows that SDG #5 (gender equality) and SDG #6 (toilet coverage) are near and constitute a cluster. The clustering results show the evidence of this fact: SDG #3 (health and well-being), SDG #4 (education), and SDG #9 (GDP) are highly interrelated and form a cluster. These three variables, which are intrinsically closely linked and have a solid interactive relationship, are referred to as "3-tuples" below.
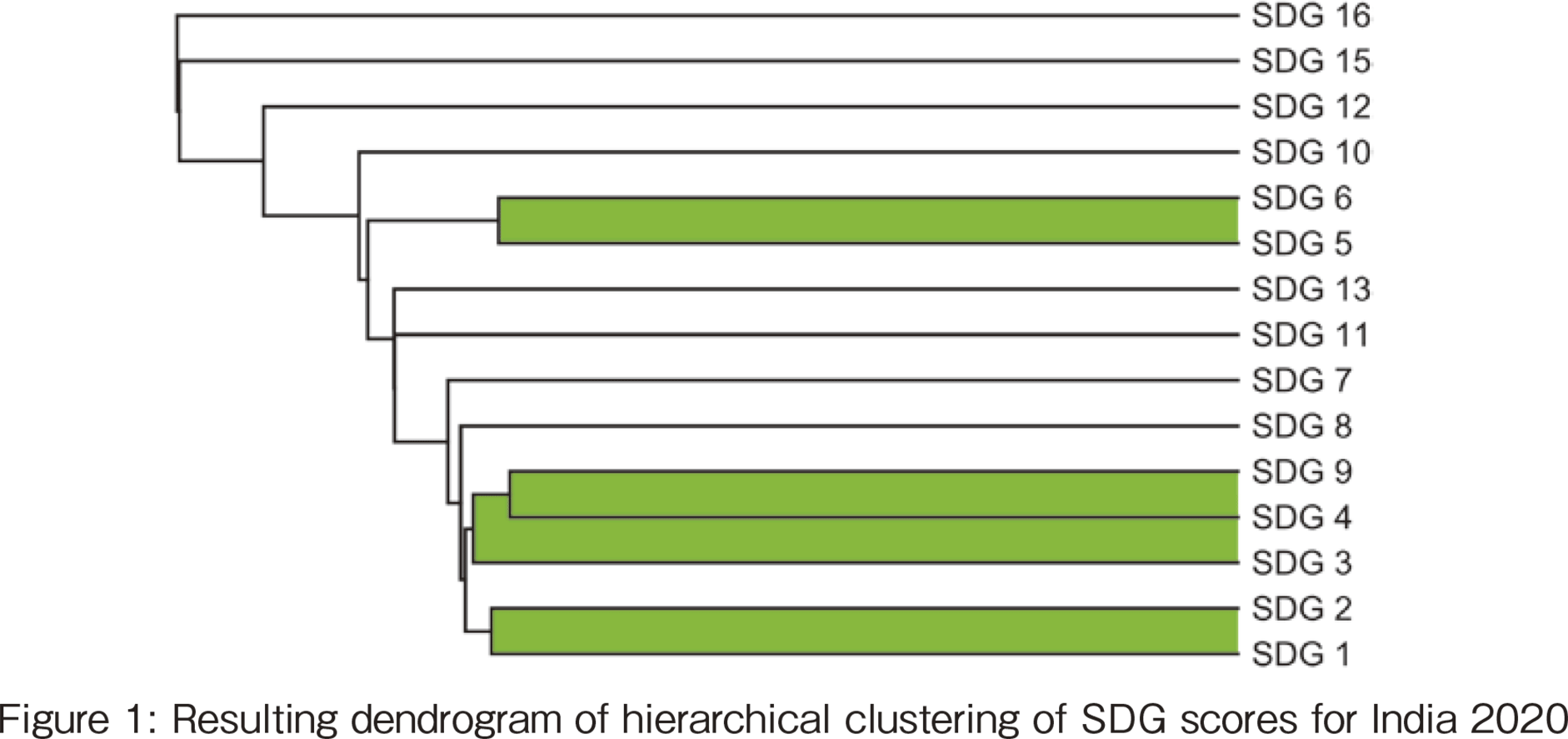
We limit ourselves to three variables in this work as the concept of three-in-one exists more frequently in the world than in other general n-variables (n>3). In such cases, the relationship between pairs of two variables is not only high, but also the relationship between three variables is strong. The triple correlation coefficient aims to find such cases directly and efficiently.
【250頁】
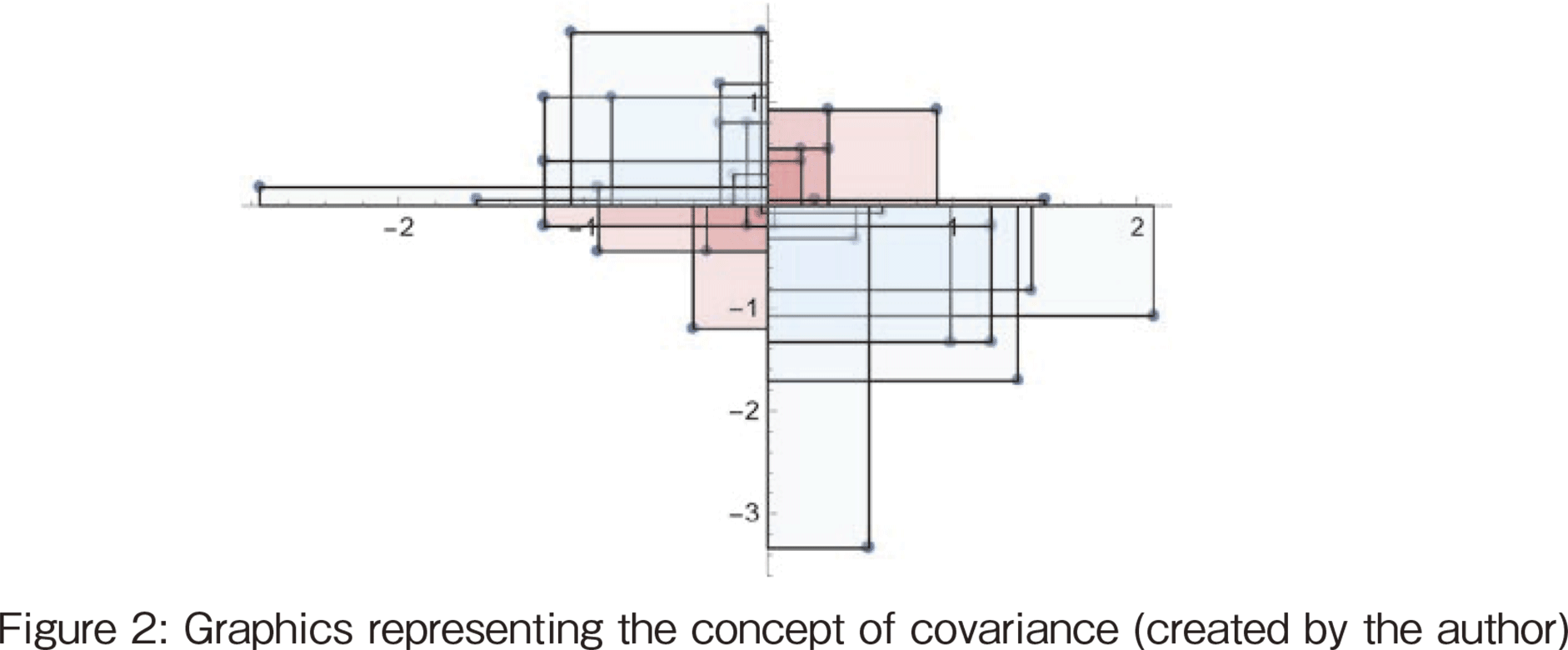
Covariance of variable x and variable y is defined as follows: Multiply the deviation of variable x by the deviation of variable y, take the sum, and divide by the degrees of freedom.
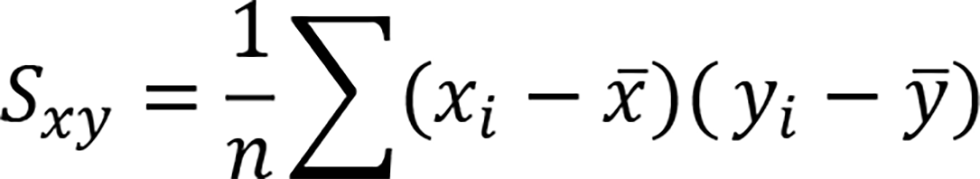
The graphical representation of this equation is shown in Figure 2. The graphs show the graphs of each data set after moving the mean value to the origin, as shown in the figure [15]. The sum of the areas of the rectangles in the first and third quadrants is calculated. There are four quadrants: in the first and third quadrants, the area value of the rectangle is positive, and in the second and fourth quadrants, it is negative. The sign of the covariance is the larger absolute value of the sum of the positive area values (product of deviations) and the sum of the negative area values. The correlation coefficient is defined as a standardized version of the covariance, and the concept is the same as in Figure 2.
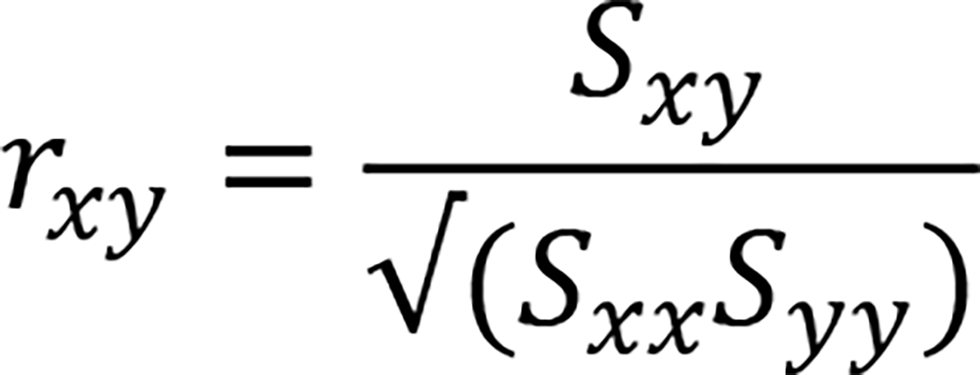
Considering the figure in this way, we can see that the covariance and correlation coefficients are the sum of the areas of the deviations, evaluating the sum total of the positive and negative area.
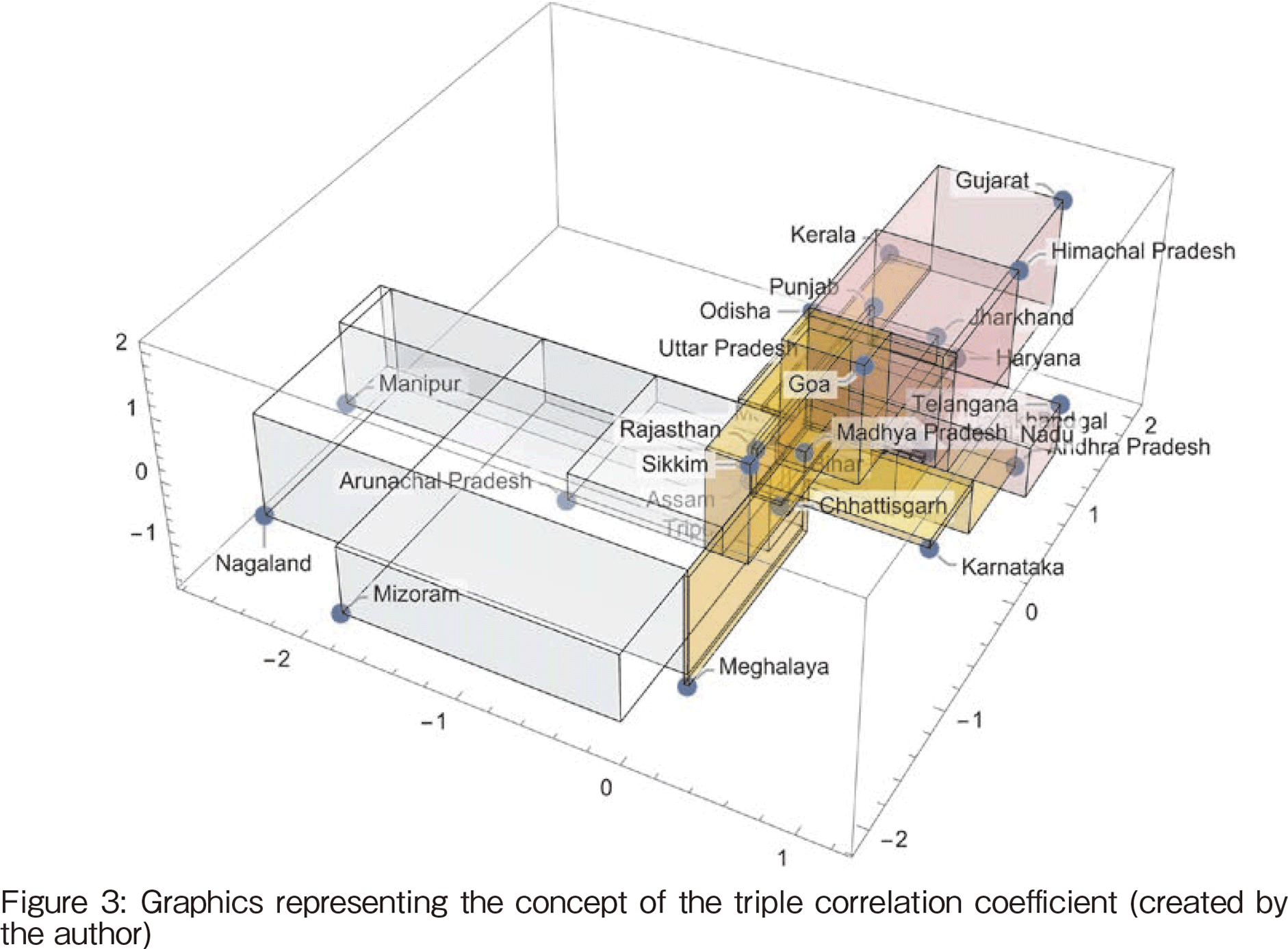
This is extended to the multiplication of the deviations of three variables. Figure 3 shows a graphical representation of the triple correlation coefficient. The definition of the triple correlation coefficient is given below. The data are standardized for each variable beforehand.
【251頁】The process of calculation is as follows:
(1) Standardize data for each variable.
(2) Calculate the absolute value of the product of the deviations of the three variables for each data.
(3) The sign is obtained by examining the values of the three variables concerned in the data and multiplying by (-1) to the m-th power, where m is the smaller number of + and -. Alternatively, only {+,+,+} and {-,-,-} are assumed to be positive, and the other values are multiplied by (-1) with absolute value.
The generalization for cases where the number of variables k is 4 or more can be made as follows. When all k variables in the data are positive, or when all k variables are negative, the coefficient is multiplied by (+1). In all other cases, multiply by (-1).
(4) For each variable, calculate the product of the deviations with their positive and negative signs, and sum them. Finally, the sum is divided by the number of the data n.
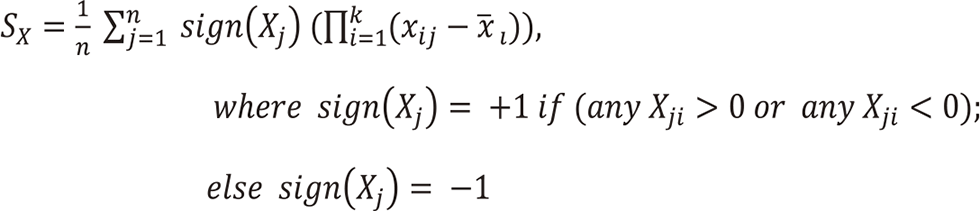
Figure 3 illustrates this. The red volume part in the portion of the space is positive. The data in the portion of the space where all three deviations are negative (in Figure 3, the light blue volume part) also have a positive sign. The data in the area of the space with orange volume in Figure 3 have a negative sign. The sum of these values leads to the calculation of the triple correlation coefficient.
3. Structural analysis of SDG 2020 data
In this section the results of the analysis of India's SDG score for 2020 are reported.
First, the triple correlation coefficients are calculated, and the top 10 three-tuples with the highest triple correlation values are shown below.
(1) {1,2,4} → 0.668,
(2) {1,2,13} → 0.599,
(3) {4,7,9} → 0.597,
(4) {1,4,9} → 0.571,
(5) {1,4,8} → 0.551,
(6) {2,4,10} → 0.543,
(7) {4,8,9} → 0.508,
(8) {4,8,10} → 0.496,
(9) {3,4,9} → 0.489
(10) {4,8,11} → 0.481
The three numbers in { } indicate the number of the SDG goals. The value shown to the right of the arrow is the triple correlation coefficient. For example, the top 3-tuple is Poverty Eradication, Hunger 【252頁】 Eradication, and Education.
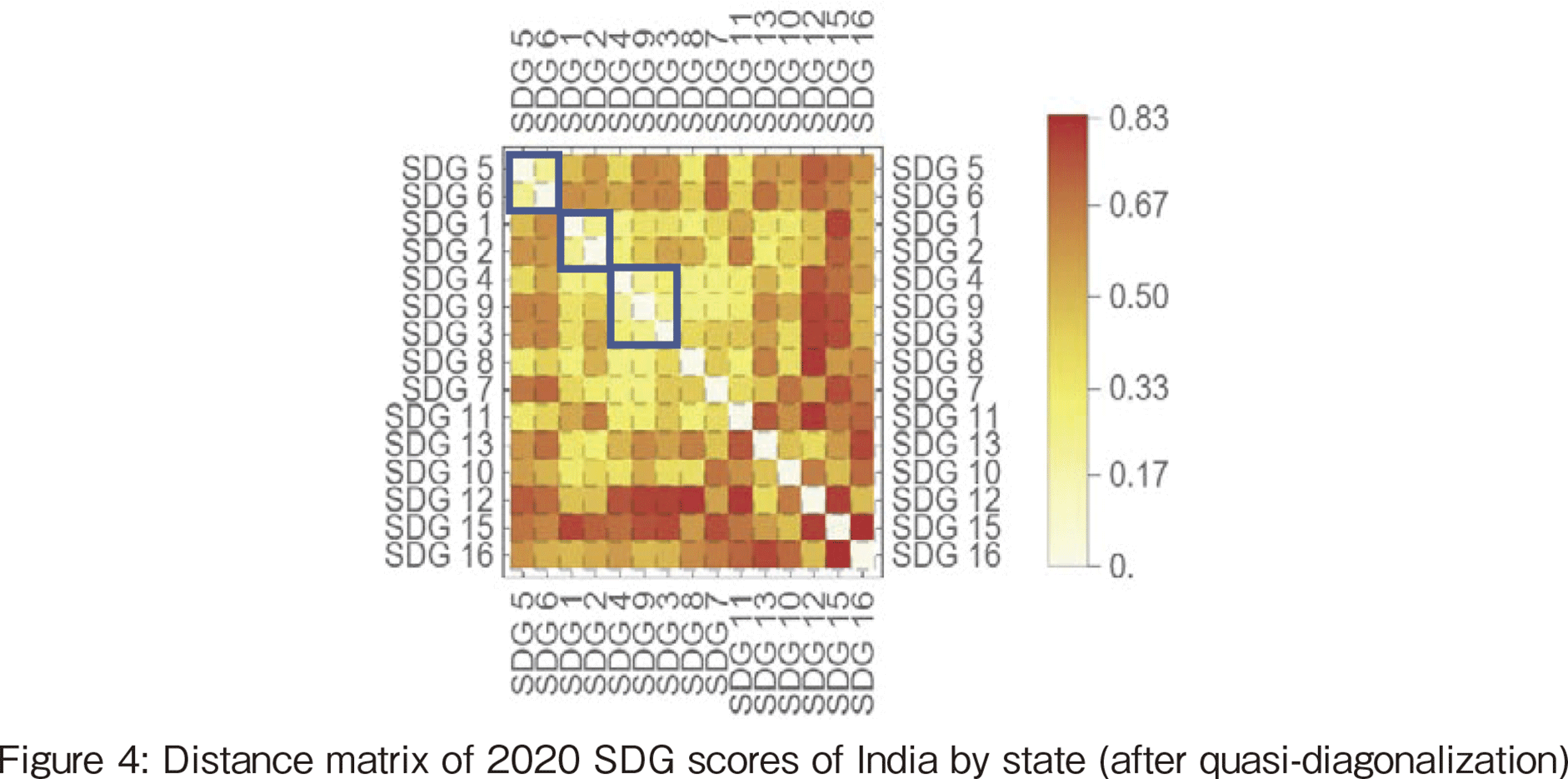
These results are compared with the hierarchical clustering results described in the previous section. Figure 4 shows the distance matrix resulting from clustering the 2020 data and then rearranging the data so that the closest distance is on the diagonal. This sorting of the data is called Quasi-diagonalization. As shown in Figure 4, white clusters appear on the diagonal. This corresponds to a cluster. The three clusters shown in Figure 4 are just one example since the the number of clusters depends on the threshold value. The dendrogram corresponding to the results of Figure 4 is shown in Figure 5, where SDGs #3, 4, and 9 are the 3-triple of health and well-being, education, and industry and innovation. These three variables are also in the top (9) of the list according to triple correlation coefficient.
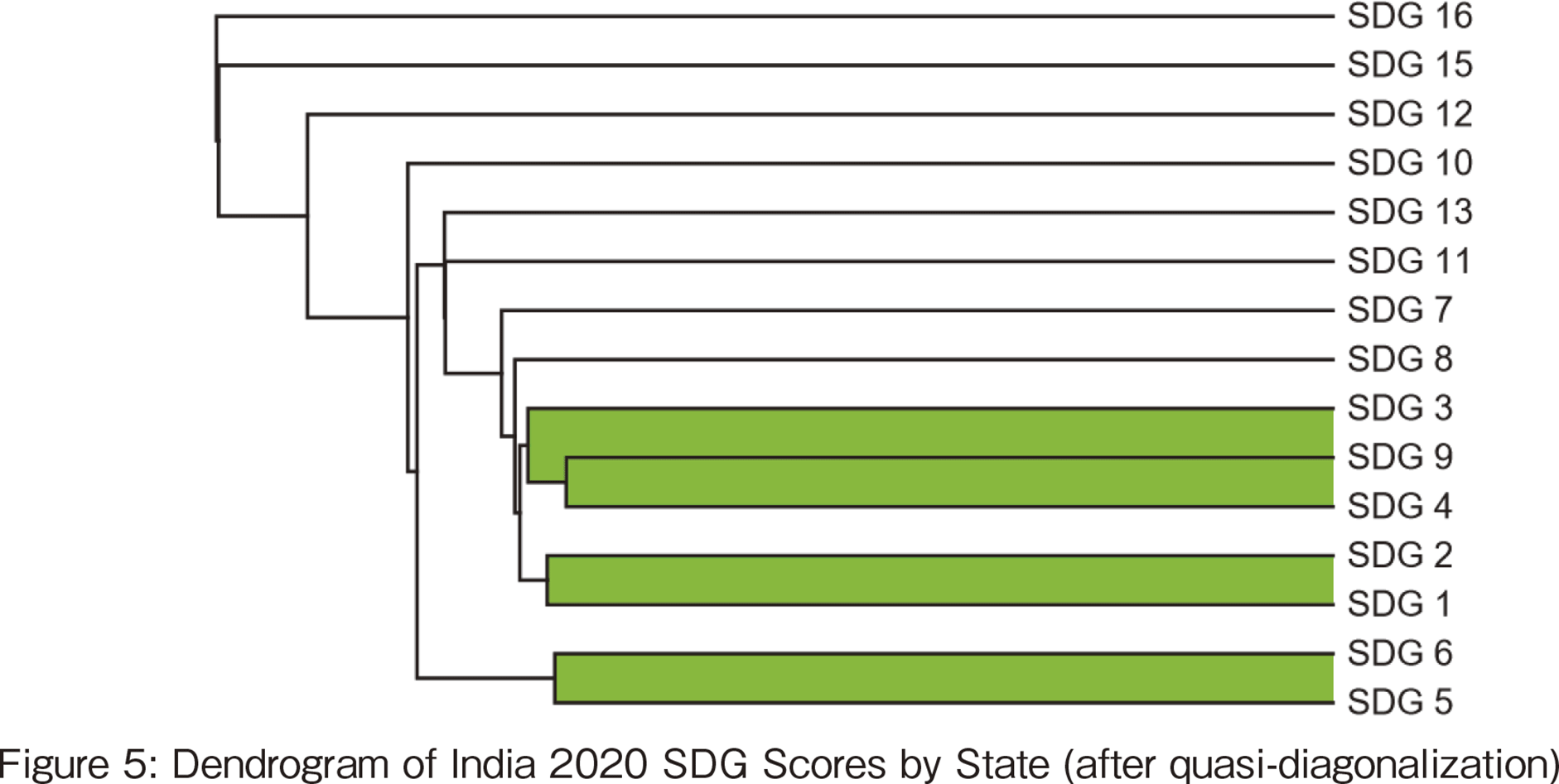【253頁】
4. Structural analysis of SDG 2019 data
In this section, the structure of India's SDG scores in the 2019 data is analyzed.
First, the triple correlation coefficients are calculated, resulting in the following values for the TOP 10.
(1) {8,9,11} → 0.550
(2) {3,8,9} → 0.502
(3) {3,8,11} → 0.439
(4) {1,2,4} → 0.387
(5) {3,6,8} → 0.386
(6) {1,3,4} → 0.384
(7) {2,4,7} → 0.380
(8) {3,9,11} → 0.372
(9) {9,11,16} → 0.329
(10) {4,5,16} → 0.323
The overall values are a little bit smaller than the triple correlation coefficient values for the 2020 results. In both the data sets, the correlation between goals is standardized for each variable beforehand, so it can be said that the correlation between goals is higher in 2020. In 2019 the top in the list is SDG #8, 9, and 11, the three goals are GDP, industry and innovation, and urban sustainability. Urban sustainability relates to housing, transportation, pollution, waste, etc. Economic growth under SDG # 8 supports urban development (SDG # 11), improves the quality of life of urban residents, and supports industrial development and innovation (SDG # 9). Robust infrastructure is also essential for the sustainable development of cities (SDG # 11). The development of cities is also considered to support economic growth (SDG # 8) and industrial development (SDG # 9). Therefore, it is reasonable that these three goals are highly related as the 3-tuple.
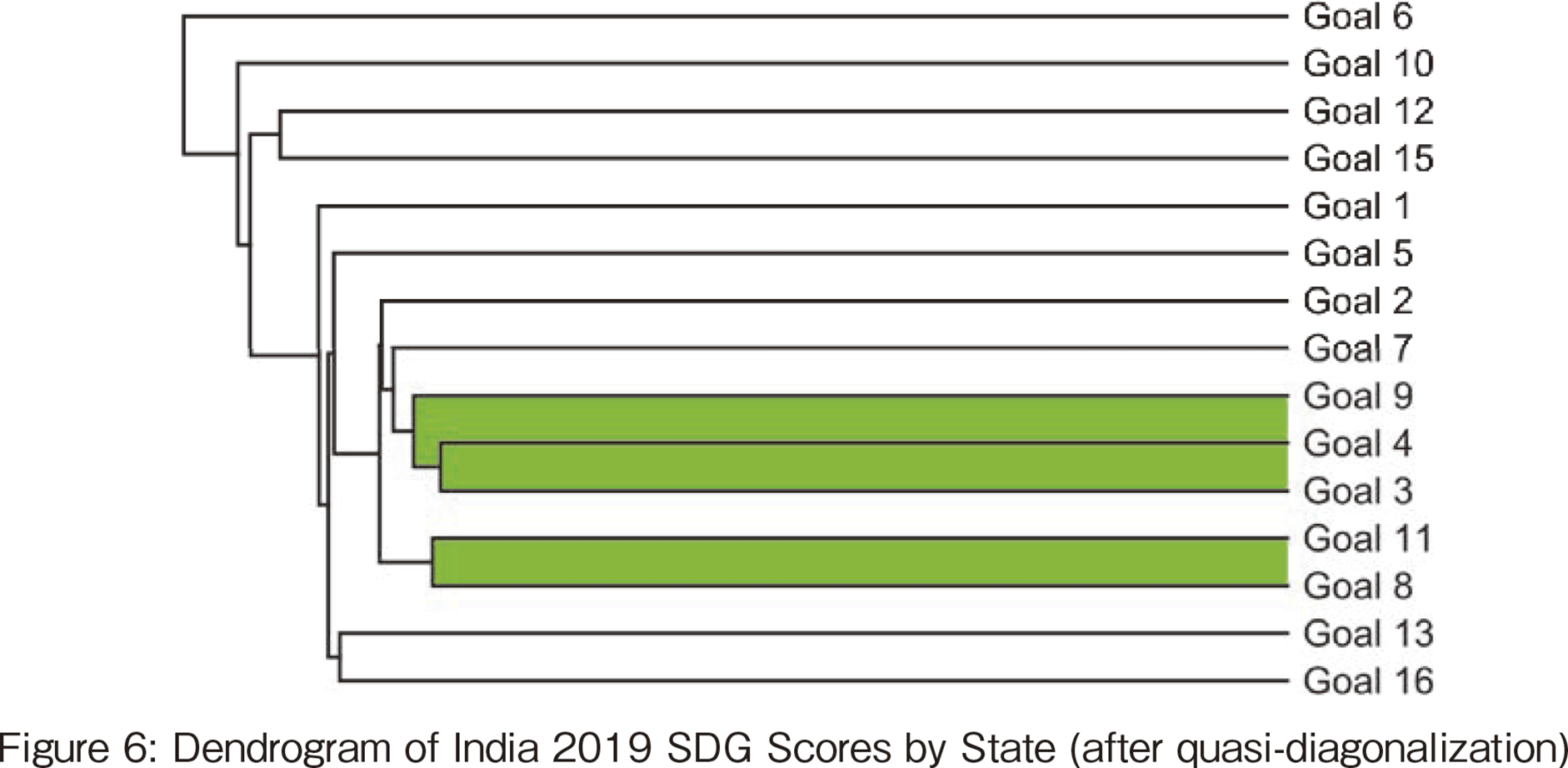【254頁】
The hierarchical clustering results are shown in Figure 6. The clustering reveals a pair of clusters for SDGs #8 and #11, and cluster for SDGs #3, #4, and #9, where SDG #8 economic growth supports urban development (SDG #11), and clusters for SDGs #3, #4, and #9, where education (SDG #4) supports industrial development and innovation (SDG #9), leading to higher levels of health and well-being (SDG #3). In the cluster of SDG #3, #4, and #9, education (SDG #4) supports industrial development and innovation (SDG #9), which can be interpreted as leading to higher levels of health and well-being (SDG #3).
5. Structural analysis of SDG 2018 data
In this section, the structure of India's SDG scores in the 2018 data is analyzed.
First, the triple correlation coefficients are calculated, resulting in the following values for the TOP 10.
(1) {Goal 3, Goal 4, Goal 5}->0.523
(2) {Goal 4, Goal 6, Goal 16}->0.464
(3) {Goal 3, Goal 4, Goal 9}->0.446
(4) {Goal 4, Goal 7, Goal 16}->0.432
(5) {Goal 1, Goal 3, Goal 4}-> 0.416
(6) {Goal 2, Goal 3, Goal 4}->0.399
(7) {Goal 3, Goal 4, Goal 7}->0.396
(8) {Goal 1, Goal 2, Goal 3}->0.369
(9) {Goal 1, Goal 3, Goal 7}->0.365
(10) {Goal 3, Goal 5, Goal 16}->0.330
The magnitude of the triple correlation coefficient is small compared to 2020 and similar to 2019, with TOP1 being {Goal 3, Goal 4, Goal 5}->15.17 for health, education, and gender equality. Figure 8 shows the breakdown of the triple correlation coefficients, with Kerala having the largest positive value compared to the others. The opposite is true for Bihar, where the deviation is negative. The reason why this 3-tuple is the TOP 1 is due to Kerala's contribution and Bihar’s one.
【255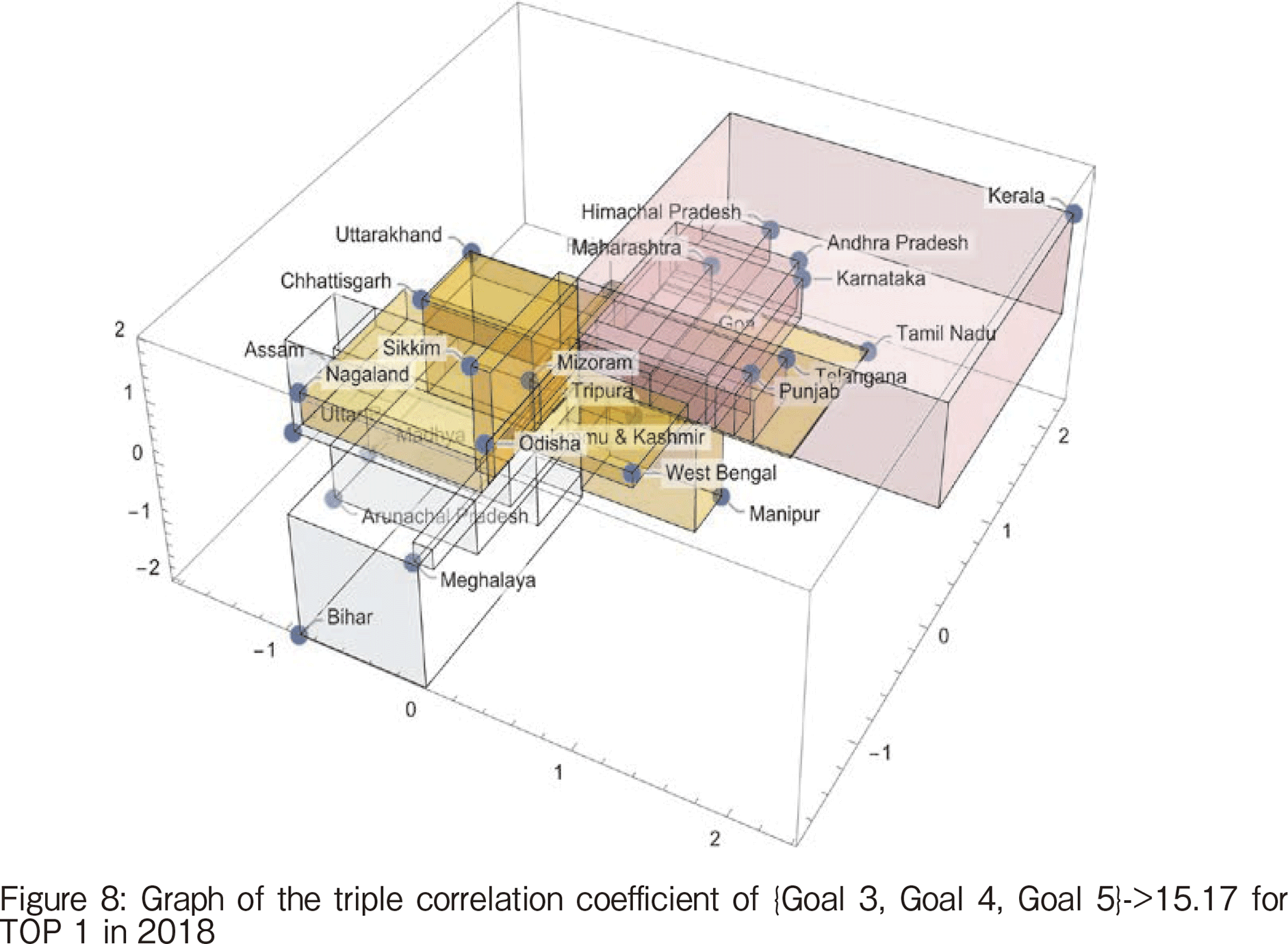頁】
【256頁】
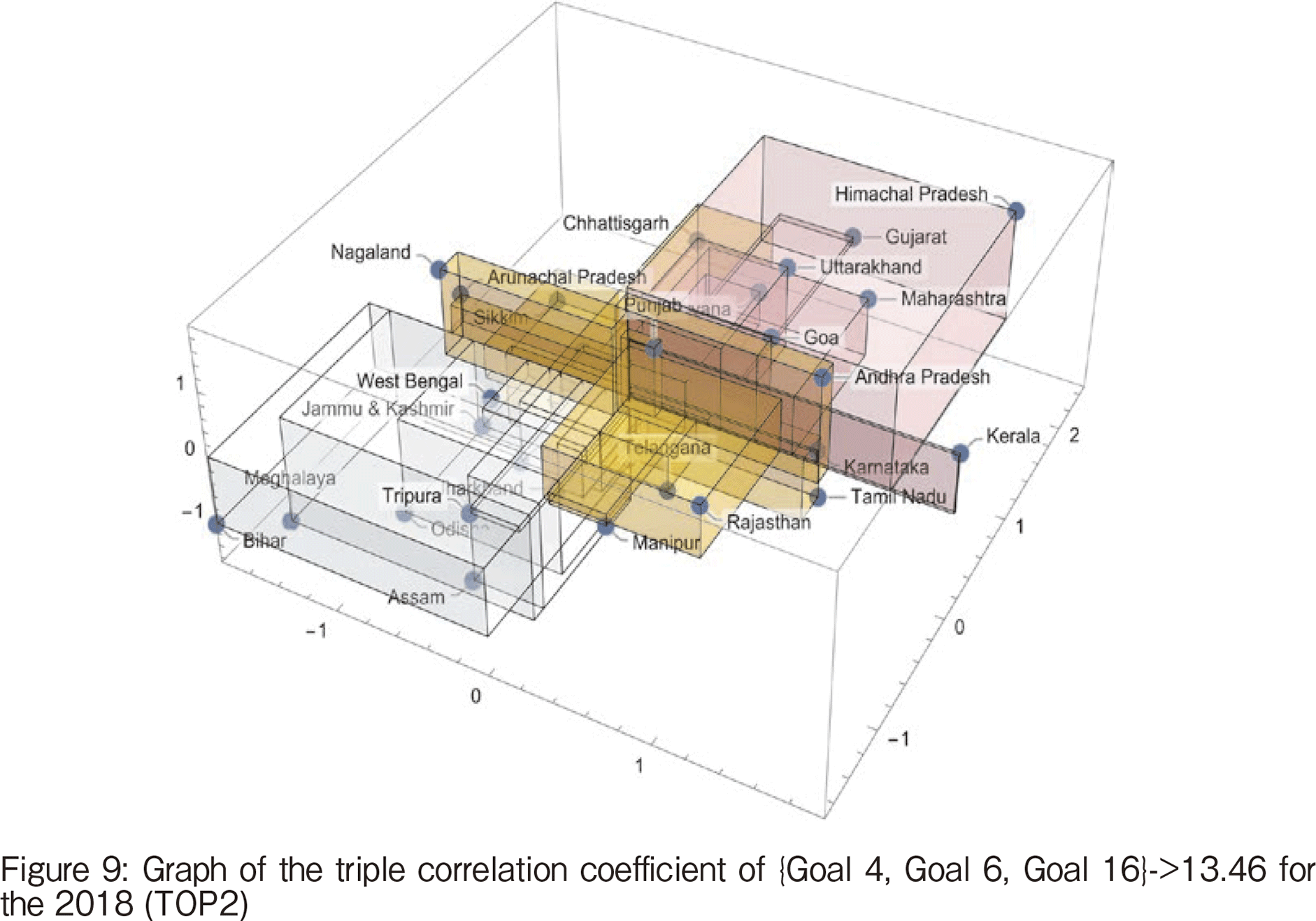
TOP2 is the 3-tuple of Education, Toilet Promotion, and Peace and Equity. The graph of the triple correlation coefficients is shown in Figure 9, and it can be seen that Kerala, which had a higher positive value in TOP1 than the others, has a higher score in education. However, a smaller Goal6 value is around average, peace and equity are not high. The state with the largest value is Himachal Pradesh. On the other hand, the negatively largest ones are Bihar and Meghalaya, in the negative direction as in TOP1.
【257頁】
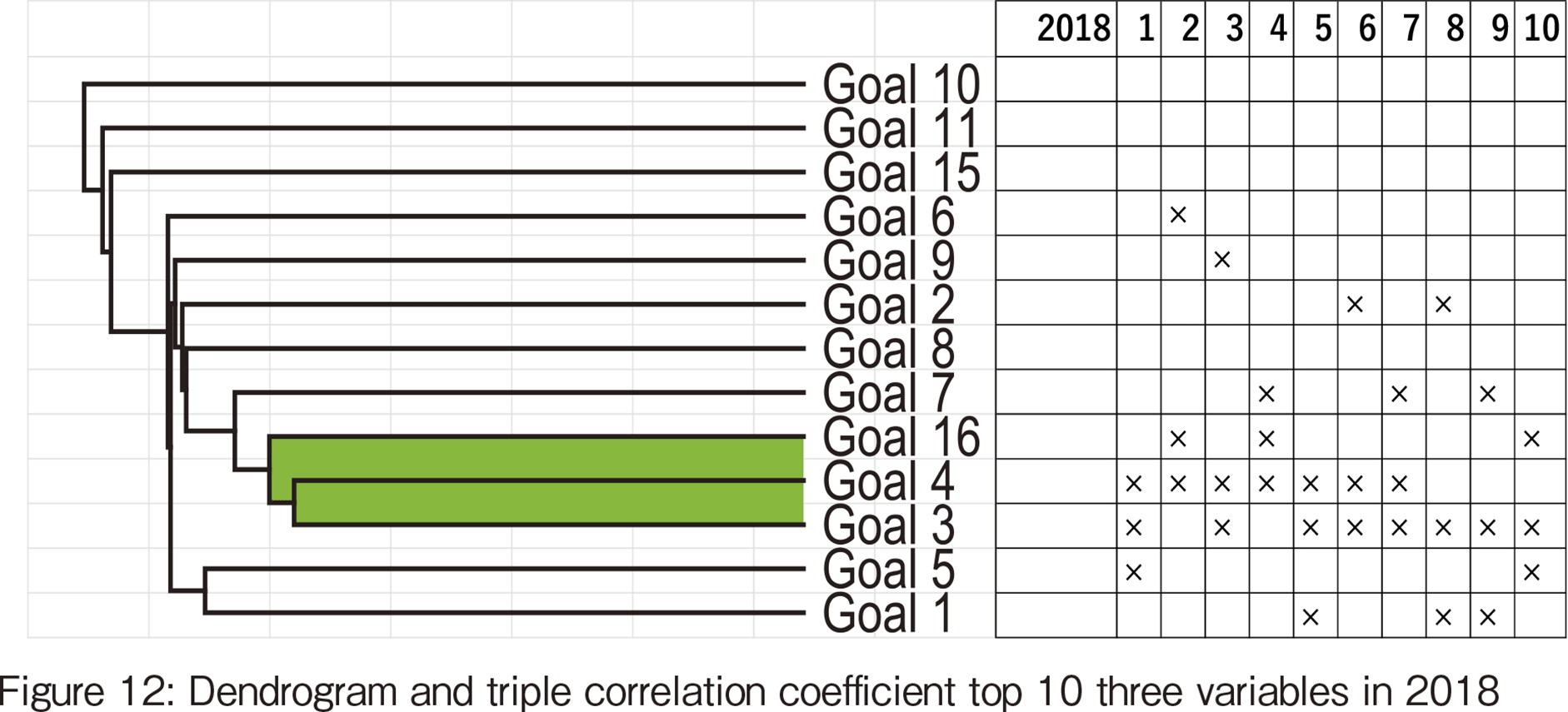
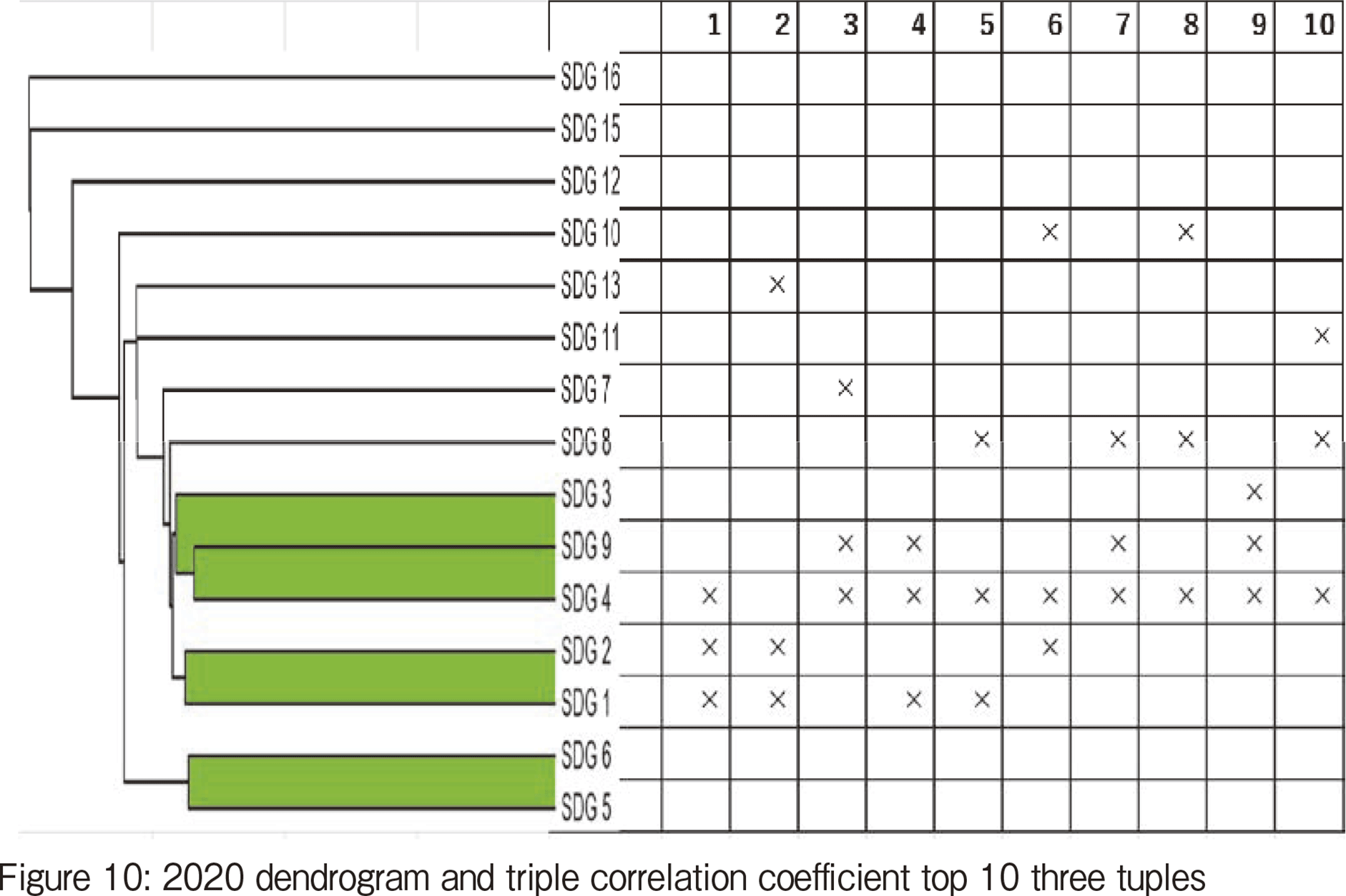
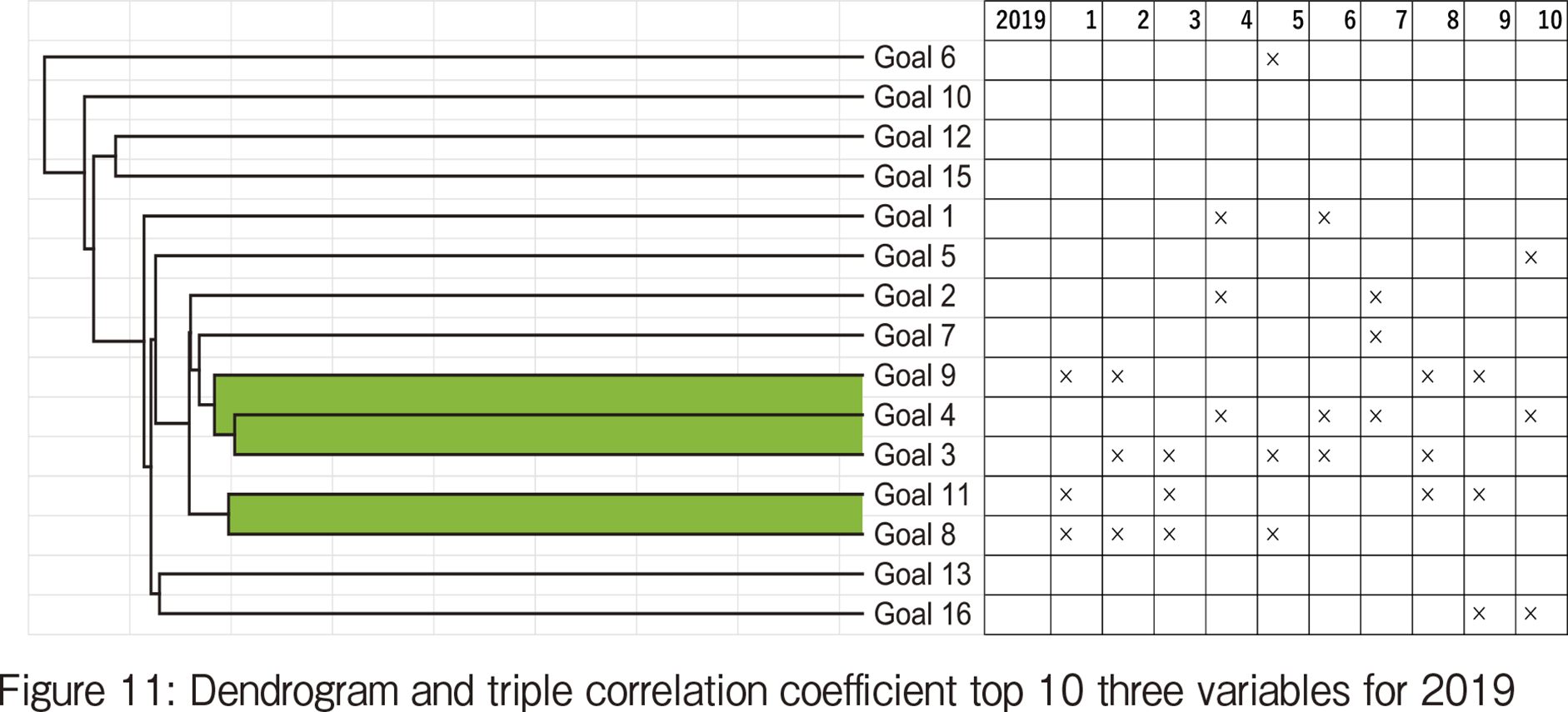
In this section, the results for 2020, 2019, and 2018 are compared and discussed. Figures 10, 11 and 12 represent the comparison of the results from hierarchical clustering and analysis of triple correlation coefficients for the SDG data of three consecutive years. The dendrogram from hierarchical clustering is placed on the left side, and the horizontal axis shows the components of the 3-tuples from TOP1 to TOP10.
In the 2018, 2019, and 2020 results, there is a general tendency for variables close in distance in the dendrogram to also appear as a 3-triple. However, SDGs #5 and #6 in 2020 do not belong to any 3-tuple despite their close distance in dendrogram. This may indicate that the two variables are highly correlated and have no relationship with the other variables. This relationship is consistent with the findings of other studies that SDG #5 is toilet coverage, SDG #6 is gender issues, and that the coverage of toilets in India has increased women's participation in society[4]. This is in line with the results of other studies [4], which have shown that toilet dissemination has improved women's social inclusion in India. This is evidence that these two SDGs are particularly closely related.
As only discovered in Figure 10, SDG #4 (Education) appears 9 times out of 10 in the triple correlation results 2020. It can be seen that education is linked to SDG 8 (economic growth) or SDG 9 (industry and technological innovation), creating a further triplet. This can represent a structure in which education is the origin of developing economic growth and technological innovation and is further linked to the third factor. Education is the cornerstone of a nation, and the high rate of occurrence of SDG #4 indicates this. To determine whether the importance of education can be found in the traditional correlation coefficient matrix, we examined the correlation matrix. Looking in the column direction, the value in the column of SDG#4 is indeed the highest. However, examining the triple correlation coefficient was easier to find spillover's influence on other variables. The triple correlation coefficient is an effective method for analyzing multiple relationships.
While counting the 3-tuples that include education in the 2019 results, it appeared four times out of 【258頁】 10. The 3-tuple of education, poverty, and hunger appeared in the top 10 list in both the years. In 2019, #3 (health and well-being) is the variable that appeared five times in the top 10, compared to the results in 2020 where SDG #3 appears only once.
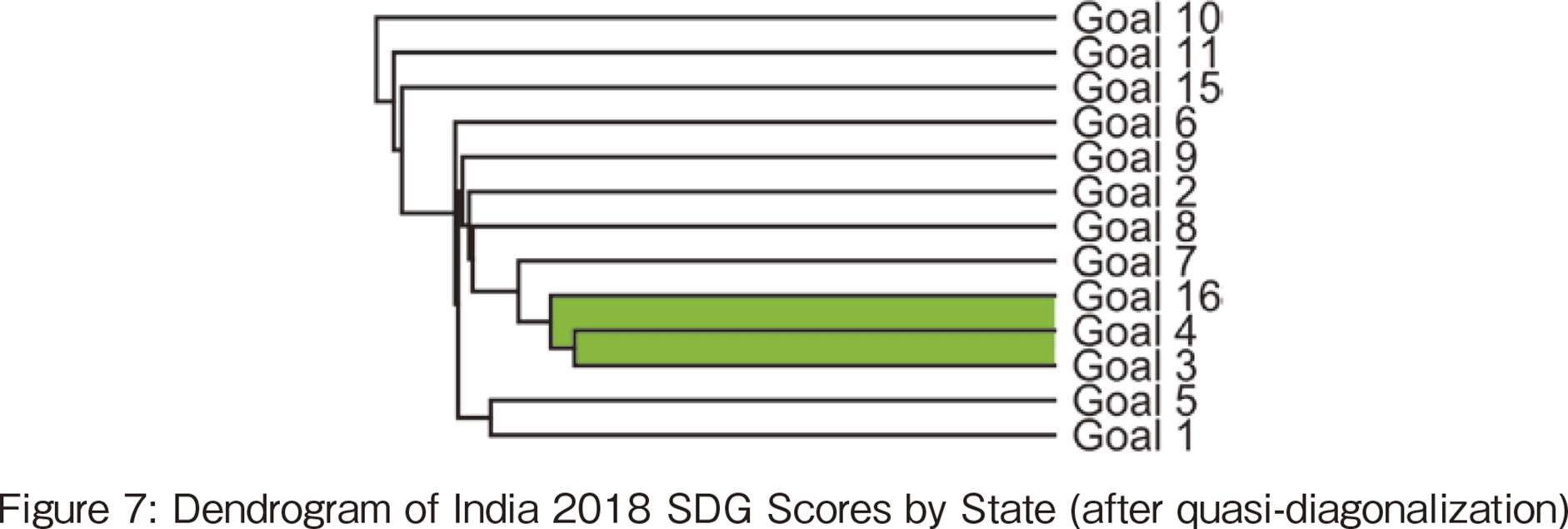
3-tuple on education appeared 7 times in the TOP 10 in 2018. Moreover, it appeared in TOP 1 to TOP 7, which shows the importance of education. However, the goal that appeared the most in the top 10 in 2018 is health and well-being (SDG#3). The time series change of SDG#3 appearances in the top 10 is from 8 times in 2018 to 5 times in 2019 and 1 time in 2020, which shows a decline but the explanation is not found.
The dendrogram in 2018 shows that the distance between the two goals, SDG#3 and #4, is the smallest, indicating they are highly related. Health allows people to have the luxury of receiving an education. People's health is considered to have a synergistic effect on each other, such as the influence of hygiene on the health of the educated. Kerala had very high values for both goals in the graphs shown in Figure 8, and Kerala is a representative of this correlation.
Concerning SDG#2(hunger), the number of its appearances increased as 2 in 2018) to 2 in 2019 to 3 in 2020. This may be related to the fact that India suffered from hunger in 2020, may be the effect of corona is responsible for this.
https://www.macrotrends.net/global-metrics/countries/IND/india/hunger-statistics[15]
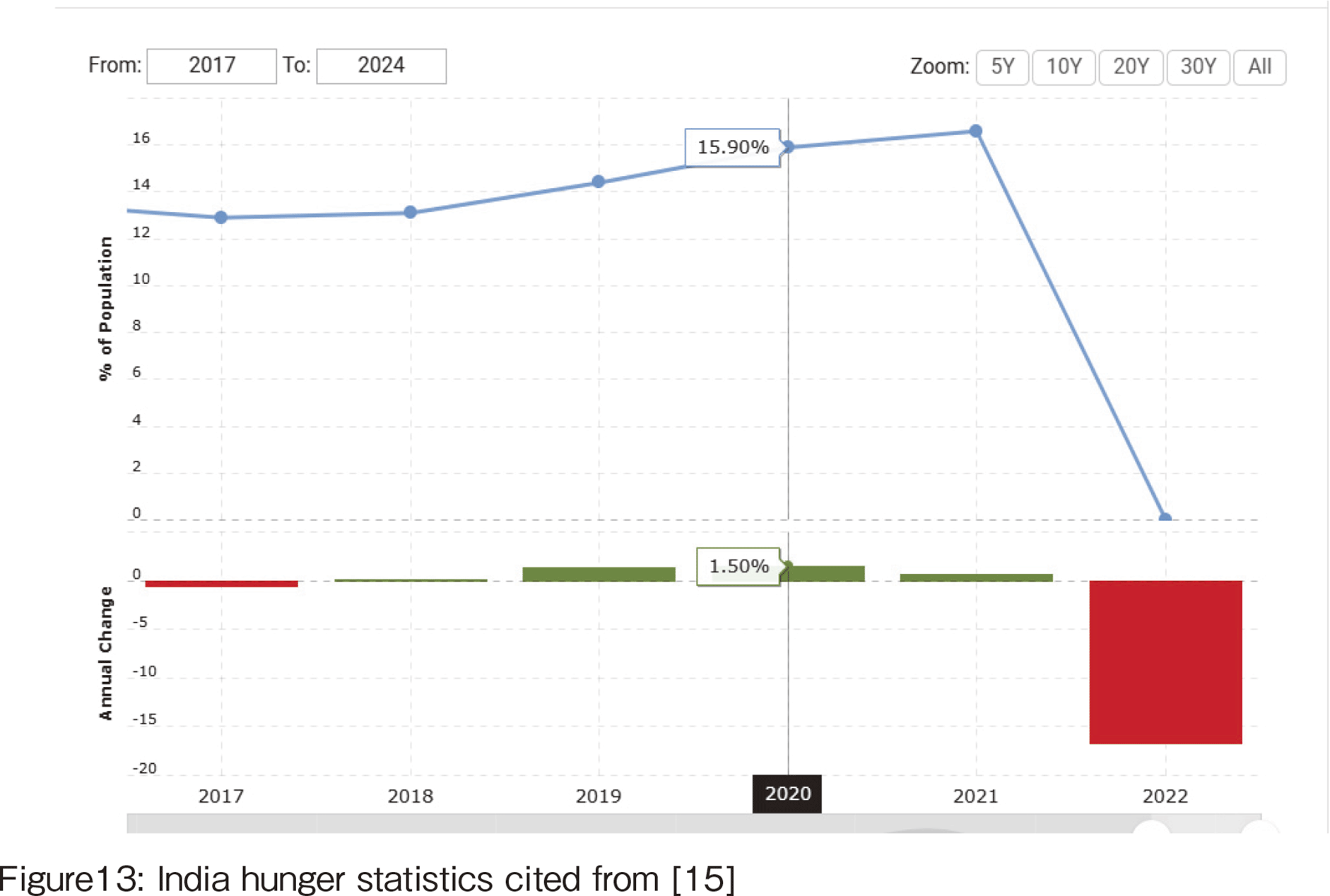
The India hunger statistics show the percentage of those who suffered from hunger as follows:
・India hunger statistics for 2022 were 0.00％, a 16.6％ decline from 2021.
・India hunger statistics for 2021 were 16.60％, a 0.7％ increase from 2020.
・India hunger statistics for 2020 were 15.90％, a 1.5％ increase from 2019.
・India hunger statistics for 2019 were 14.40％, a 1.3％ increase from 2018.
【259頁】
Figure 13 shows the percentage of people suffering from hunger in India, which increased from 2018 to 2021. The impact of COVID-19 in India increased the hunger rate from 2020 to 2021. The high incidence of hunger and poverty in the SDG analysis results for 2020 may be related to this high hunger rate.
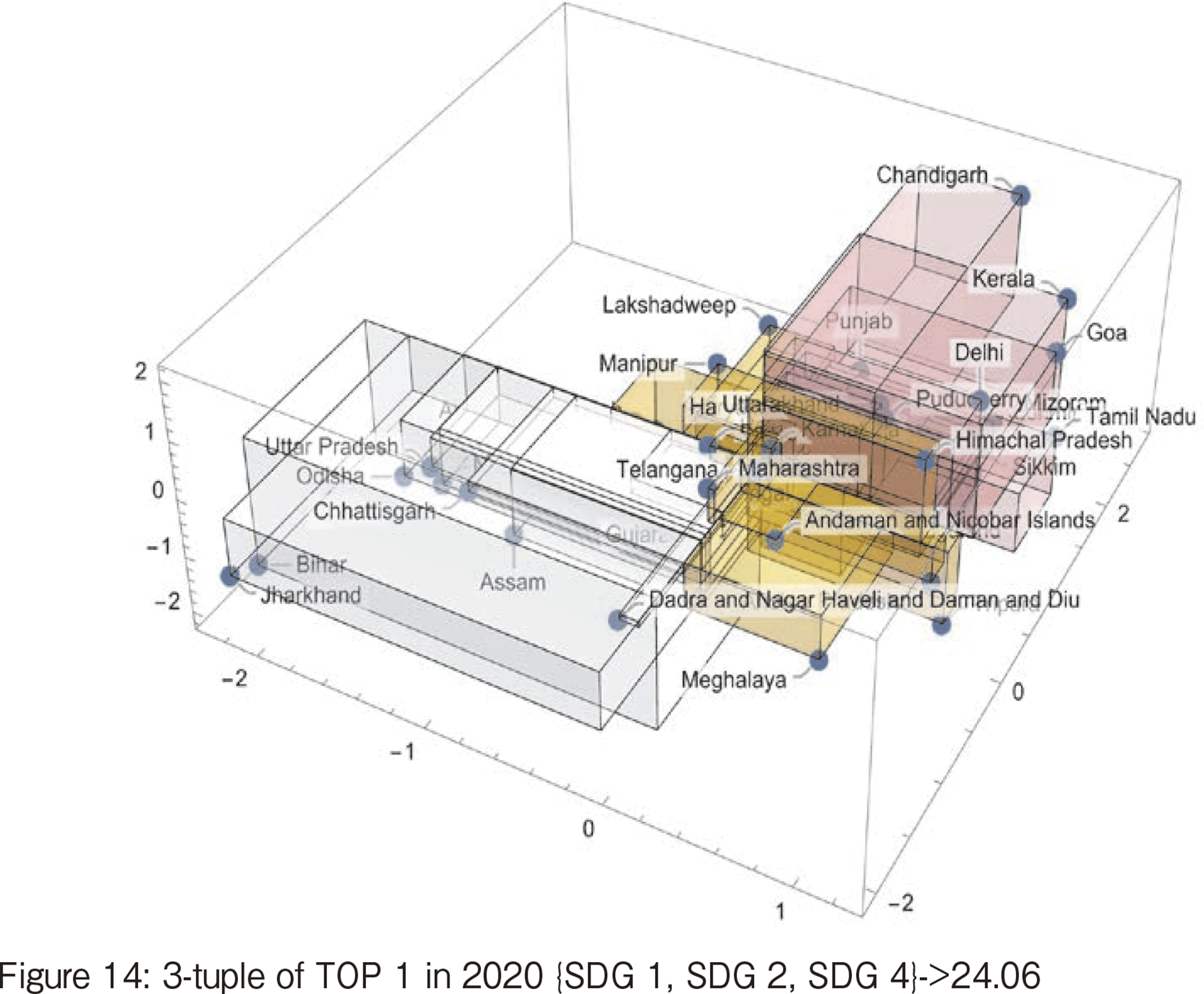
Figure 14 shows the TOP1 3-tuple {SDG 1, SDG 2, SDG 4}->24.06 in 2020. Looking at these three goals, most states have two options: all are positive, or all are negative. Only a few states have only one negative value with small values. This indicates that there is a polarization due to hunger and other factors. The provinces with the highest absolute value of the cube of the deviation are Jharkhand and Bihar. These two states belong to a small number of states with very poor scores on the three goals, and their presence seems to increase the value of the triple correlation coefficient.
【260頁】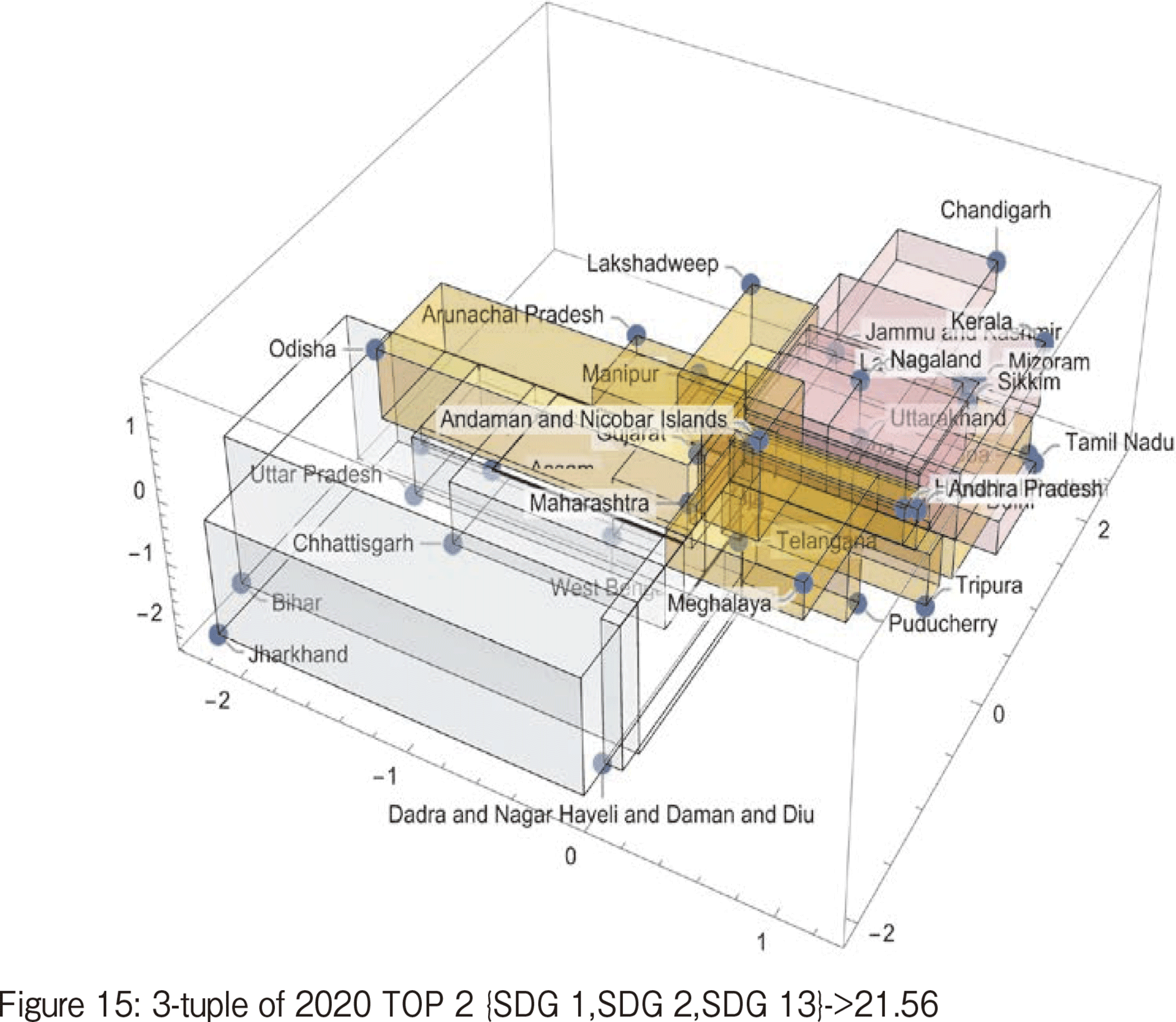
Looking at Figure 15, which illustrates TOP2 in 2020, the dominant factors of the triple correlation are SDG#1 and SDG#2. Jharkhand and Bihar offer large contribution to the triple correlation.
【261頁】
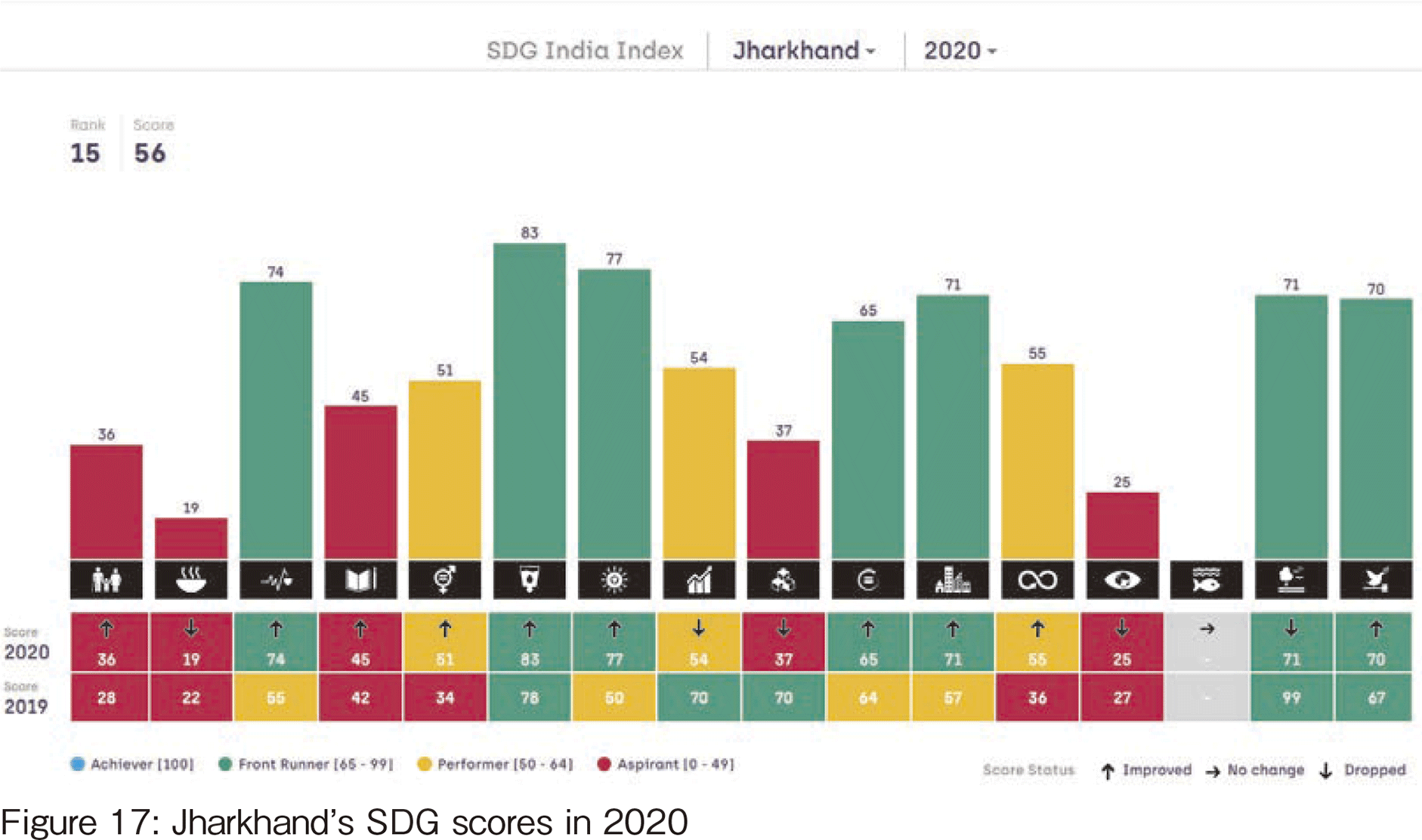【262頁】
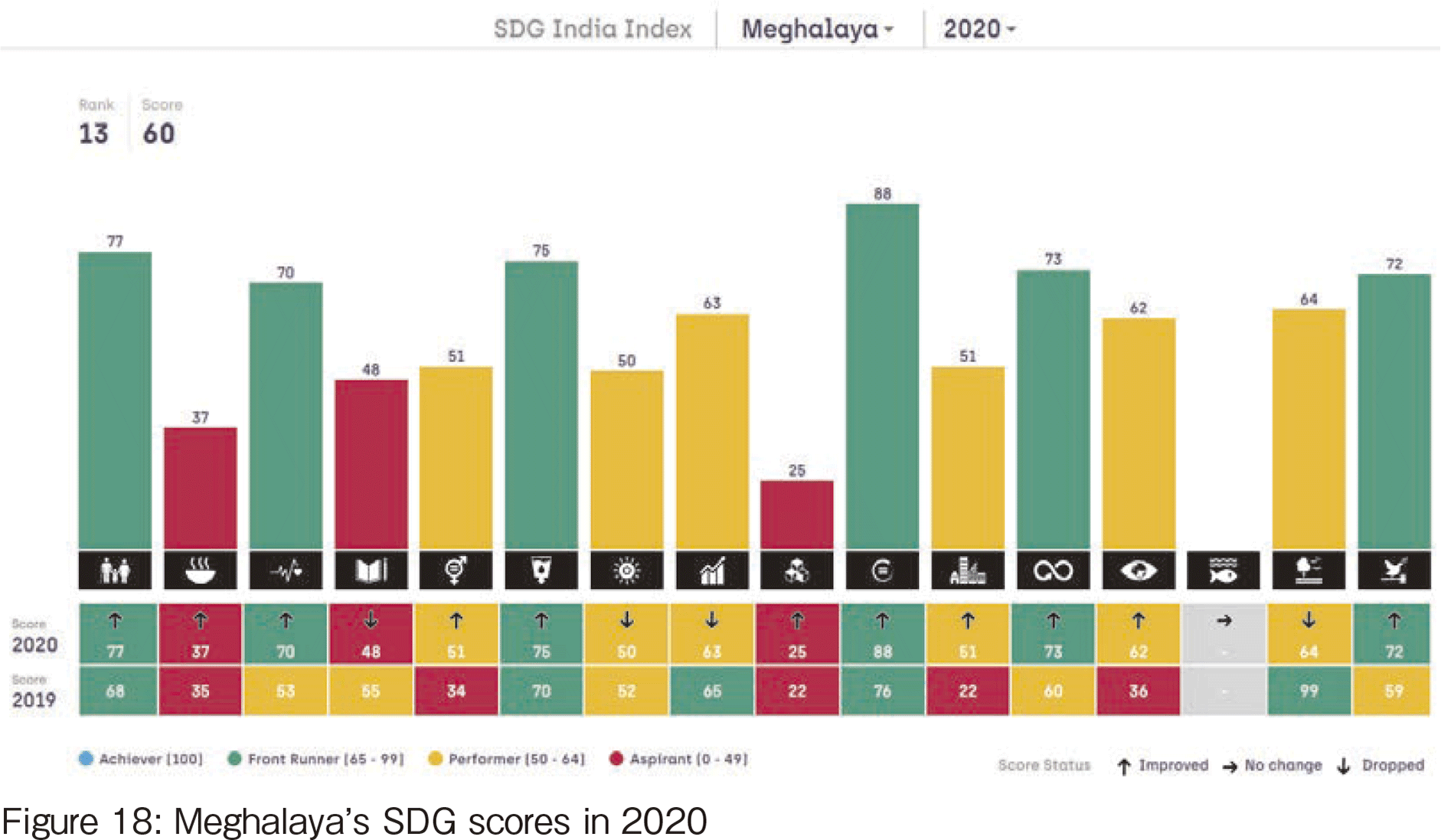
Figures 17 and 18 show the 2020 scores of Jharkhand and Meghalaya respectively, which are cited from [5]. From there, we found that these states must have suffered much more from hunger then.
Two things emerged from the discussion. First, the influence of education on the other goals is significant, and second, the plight of a small number of states due to poverty and hunger caused by COVID-19 in 2020. First, education seems to have the most significant impact on the SDGs in India, followed by "industry and innovation" as the most influential goal. The reasons why the importance of education (SDG 4) and industry, innovation, and infrastructure (SDG 9) emerge prominently in the analysis of the 2020 and 2019 SDGs in India are discussed below. Educational growth in India is high, and many families view education as a top priority. In India, education is widely recognized as the key to economic growth and social progress, and it is believed to enable people to improve their standard of living by acquiring skills, especially in ICT, through education and to gain better job opportunities. India is known worldwide as the center of the IT industry, especially in Bengaluru, Hyderabad, Pune [16], India's IT sector's success has increased education's importance, especially in science, technology, engineering, and mathematics. STEM education is a driving force behind India's economic growth and technological innovation.
It was also found that hunger is a feature of 2020 that impacts other goals. The impact of COVID-19 increased the rate of hunger, which in turn had a significant impact on other goals, especially education.
7. Related Works on Multiple Correlation
We have used triple correlation coefficient proposed by us in a previous work for the analysis in this paper. In this section, we would like to present some research works by other authors found in the 【263頁】 literature in which similar concepts are used. Basically we will here describe two concepts with similar names as of our proposed measure. These are (1) multiple correlation coefficient R in a regression and (2) auto triple correlation in signal processing. The names of the two terms are similar to our triple correlation. However, they are completely different from our proposed measure.
(1) Multiple Correlation Coefficient R in a multiple regression [17]
In a multiple regression where there are N subjects, and a dependent variable Y from a set of J independent variables, the quality of the prediction is evaluated by computing the multiple coefficient of correlation denoted RY.I,…,J2 where y = Xb with b = ( XT X )-1 XT y
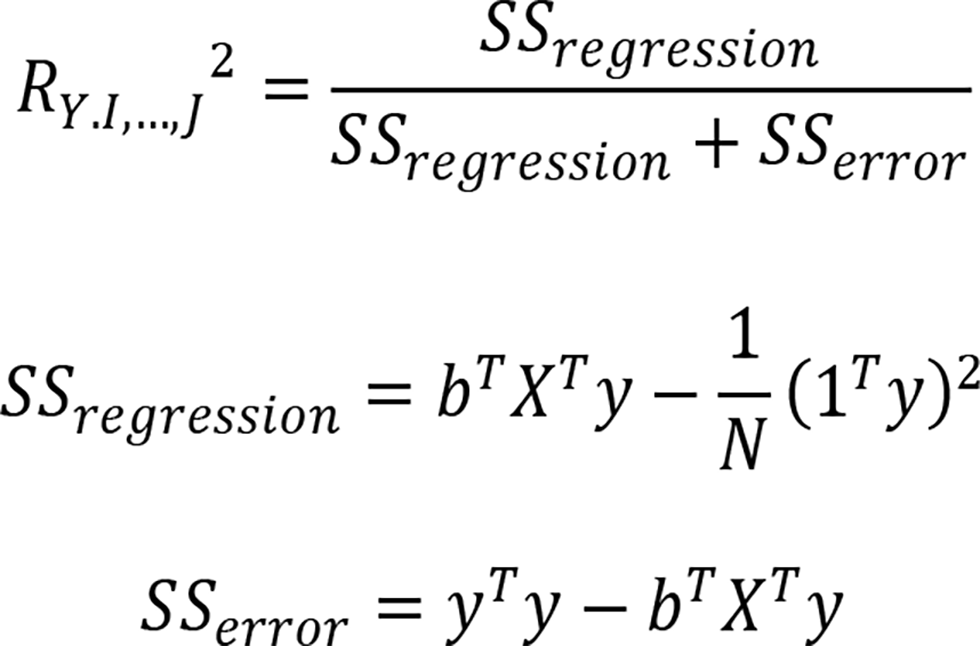
This Multiple Correlation Coefficient R is defined in a regression to evaluate the prediction accuracy. Now for j=3, we can have a triple correlation coefficient, but the definition and the equation is different from our definition of triple correlation coefficient.
(2) Auto triple correlation in a signal processing [18]
In the area of signal processing, the term “triple correlation” has been defined and used. In [18], Lohman says one of the earliest references on triple correlations is found in [19], as far as they know. The auto triple correlation has been defined as
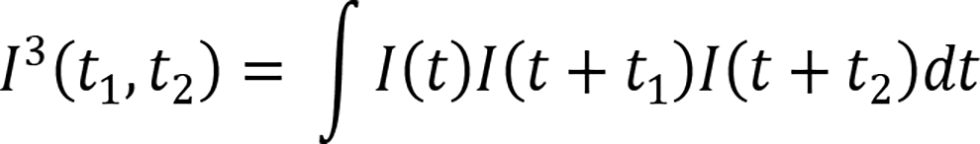
The triple correlation is less popular than the standard (double) correlation for several reasons: the standard (double) correlation is sometimes easier to observe and to process. On the other hand, the triple correlation knows more about the signal I than does the ordinary autocorrelation because it is in some ways more sensitive.
This auto triple correlation defined in a signal processing is completely different from our defined triple correlation.
In this paper, the structural analysis of India's SDG scores has been conducted using proposed triple correlation coefficient and hierarchical clustering. Conventional correlation coefficient is based on the relationship between two variables and cannot be used to simultaneously determine the relationship between multiple variables. In this study, the triple correlation coefficient has been defined to obtain the relationship among three variables at once and is used in the analysis.
Using data from Indian state-by-state SDG scores for 2020 and 2019 and 2018, we found three pairs 【264頁】 of SDG goal variables that are highly correlated in 2020 than in 2018 and 2019. The 3-tuple with the highest correlation is found to consists of the poverty, hunger, and education; the second 3-tuple is the poverty, hunger, and climate change 3-tuple; the third is education, innovation, and clean energy; and the fourth is the poverty, hunger, and climate change. Education also appeared nine times in the Top 10 3-tuple for 2020. This suggests that education is fundamental for improvement of the other SDG goals. The combination of education and technological innovation as the core and relation of them with other SDG goals are found.
Furthermore, the triple correlation coefficient results for 2019 show that technological innovation has a significant impact. Technological innovation appeared five times in the TOP 10. Education and technological innovation are cornerstone elements of India's strong IT services sector. The high interest in science, technology, engineering, and mathematics (STEM) education in India is a driving force behind India's economic growth and technological innovation. The results of this analysis indicate the importance of STEM education in India and the factors that contribute to its success.
Acknowledgment
This work was partly supported by a special project of the Institute of Oriental Studies, Gakushuin University (2020-2024), and a special project of the Computer Center, Gakushuin University (2024).
References
[1] unicef, "SDG club." [Online]. Available: https://www.unicef.or.jp/kodomo/sdgs/about/
[2] T. Hashimoto, Y. Shirota, and B. Chakraborty, "SDGs India Index Analysis using SHAP," International Electronics Symposium (IES) 2022 IEEE, Surabaya, Indonesia and online, pp. 461-465, 2022.
[3] S. Bonthala, Y. Shirota, and B. Chakraborty, "SDGs Gender Equality Analysis in India by using SHAP Interpretation," IEEE 1st International Conference on Optimization Techniques for Learning (ICOTL) IEEE, pp. 1-6, 2023.
[4] Y. Shirota, T. Hashimoto, B. Sreekanth, and B. Chakraborty, "India SDGs Analysis on Well-being -How to Effectively Achieve Well-being -," 学習院大学、東洋文化研究, Journal of Asian cultures, vol. 26, pp. in printing, 2024.
[5] NITI_Aayog, "SDG India Index," 2024. [Online]. Available: https://sdgindiaindex.niti.gov.in/#/ranking
[6] 白田由香利 and バサビ・チャクラボルティ，"トリプル相関係数の提案," 電子情報通信学会、信学技報(WebDB 2024), pp. (in printing), 2024.
[7] 東京大学教養部統計学教室，"統計学入門," 東京大学出版会，1991.
[8] 狩野裕 and 三浦麻子，AMOS、EQS、CALISによるグラフィカル多変量解析 : 目で見る共分散構造分析 現代数学社，2020.
[9] 村瀬洋一，高田洋，and 廣瀬毅士，SPSS による多変量解析 株式会社 オーム社，2007.
[10] T. Hastie, R. Tibshirani, J. H. Friedman, and J. H. Friedman, The elements of statistical learning: data mining, inference, and prediction Springer, 2009.
[11] 小塩真司, 共分散構造分析はじめの一歩: 図の意味から学ぶパス解析入門 アルテ，2010.
[12] J. F. Hair Jr, B. J. Babin, and N. Krey, "Covariance-based structural equation modeling in the Journal of Advertising: Review and recommendations," Journal of Advertising, vol. 46, no. 1, pp. 163-177, 2017.
【265頁】[13] 狩野裕，"構造方程式モデリングは，因子分析，分散分析，パス解析のすべてにとって代わるのか?, " 行動計量学，vol. 29, no. 2, pp. 138-159, 2002.
[14] I. Government, "Toilets Built Under Swachh Bharat Mission," 2022, February 10. [Online]. Available: https://pib.gov.in/PressReleaseIframePage.aspx?PRID=1797158#:~:text=Government％20of％20India％20provides％20technical,and％20cleaning％20of％20the％20toilet
[15] I. H. Statistics", "India Hunger Statistics 1960-2024," 2024. [Online]. Available: https://www.macrotrends.net/global-metrics/countries/IND/india/hunger-statistics
[16] V. Dey, "Bengaluru Is The Most Desired Hub For GCCs," in GOA Institute of Management, 2021/07/21. [Online]. Available: https://analyticsindiamag.com/bengaluru-is-the-most-desired-hub-for-gccs/
[17] H. Abdi, "Multiple correlation coefficient," Encyclopedia of measurement and statistics, vol. 648, no. 651, pp. 19, 2007.
[18] A. W. Lohmann and B. Wirnitzer, "Triple correlations," Proceedings of the IEEE, vol. 72, no. 7, pp. 889-901, 1984.
[19] D. R. Brillinger, "Time series; data analysis and theory. New York: Holt, Rinehart and Winston," Inc, 1975.