【247頁】

IPO初値乖離率の月効果とジャスダック市場のアノマリー分析

辰巳　憲一、桂山　靖代

1　はじめに

ファイナンス分野では様々なアノマリーが見出され分析されてきたが，IPO（新規株式公開）分野のアノマリーとは，一般に，公開価格のいわゆるアンダープライシングを指し，初値が公開価格を超えることが多い事実を指す。この現象を統計学的に正確に把握し，情報の非対称性やオークションの方式などによって，それを経済学的に説明する努力がなされてきた。

また，IPO後の長期（36ヵ月）株価パフォーマンスが悪い現象も，アンダープライシングと対にしたオーバープライシングという言葉で語られ，アノマリーの1つになっている（巻末附録には日本のその数値を示した）。

他方，本稿では，アノマリーのもう1つの局面である，暦の上で観察される時系列的な現象をみてみる。つまり，初値乖離率は，それが属する月によって，特別な変動をするかどうかを時系列データから検証する。以下では，経済的な新行動仮説を提示し直接検証するわけではないが，著者が整備したデータに対して正当な統計学的処理を行い，どのようなタイプのアノマリーが成立しているかを示すことになる。さらに，本稿では，日経ジャスダック平均に見られる曜日効果の原因について，IPOの観点から考察する。

ここで用いるデータは主として1996年1月から2003年12月までの期間，特にJASDAQにIPOした670銘柄，の初値乖離率である。このうち1996年から1999年まではJASDAQ・IPO346銘柄の様々な局面を分析した辰巳・桂山［10］［11］［12］［13］で分析したものとまったく同一である。

2　研究のねらい

2-1　暦の上にみられるアノマリー

米国では，月曜日の株式投資収益率が他のどの曜日の収益率よりも低く，月曜日効果と呼ばれている。また，金曜日の収益率も低いことが特徴として指摘されている。このように1週間【248頁】の株価の動きにはある一定のパターンが知られてきた（1。

さらに，株式投資収益率には，月についても一定のパターンが指摘されてきた。1月は特に高い収益率が観察される。英国のように，税制に絡んで4月にも特徴的な動きがある国もある。エコノミストのなかには2，8月の需要涸れを指摘する人もいる。それゆえ，12ヵ月の間一定のパターンを毎年繰り返しているのではないかという仮説が本稿の検討対象になる。

2-2　曜日効果について

以上の曜日効果についての現象は，従来，米国などに当てはまったにすぎなかった。日本では，1980年代までのデータでは，欧米諸国とはまったく違う，火曜日効果が提示されたことがある。この結果は，著者の判断では，基本的なデータ処理や計測法などの点が不明確，不正確であるから，試算の域を出ていない。

実際，Tong［14］は1974年から1994年までの5412の日経平均のデータ（一部に，過去行われた土曜日営業のデータを含む）で，他の先進国並の月曜日効果を検出している（2。それでは，さらに最近の1989年1月から2003年8月までのデータでは，実際，どうなのかを調べ，また非線形時系列分析法を日本のデータに適用してみたのが宮野・辰巳［4］［5］の研究であり，一週間パターンは顕著に観察された。

2-3　月効果と曜日効果の関係

既述の2つの効果を重ねると，週の5日間パターンは年の12ヵ月パターンの波／うねりのなかにあることになる。従来，月効果の分析は，曜日効果とはまったく独立に，月末終値（曜日を問わず）データの単純回帰式における月ダミー変数の有意性でなされた。

まず指摘しておくべきは，この月ダミー変数法には，多重共線性，分散不均一性などの，大きな欠点がある（Chien-Lee-Wang［2］）ことである。本稿はこの方法をとらない。

そして，株式投資収益率に観察される月効果は，月末の曜日を問うことなく，月末終値データを用いて回帰分析しており，曜日効果を排除して計測されていない。何年にも渡って月末営業日の曜日が偏れば，月効果に曜日効果が紛れ込むことになる。これら2つの効果を分離し，しかも相互効果を検出する必要がある（3。

また，さらに重要なことに，従来の研究は月末終値だけに観察される特殊な要因を検出しているにすぎないのかもしれない。月効果を説明する経済仮説はどれも唯一の要因として納得で【249頁】きるものではないが，諸仮説が注目する株式市場参加者の行動や制度はかならずしも月末だけに起こる・該当するものではない。月末の数日以上をかけて，場合によっては月中毎日行われる行動なのである。月中毎日該当する制度・行動なのである。そこで，月中株価のすべてに観察される月効果を検出する必要がある。本研究はこれらの批判を回避している。

2-4　その他のアノマリーとの関係〜米国のケース

1月効果は，1月には小型株が大型株を超える高パフォーマンスを示す事実を測っていることが，1980年代前半にReinganum［6］などによって明らかにされた。この現象が広く知られるようになるのは，最初の発見者であるRozeff-Kinney（参考文献は省略）が上場銘柄で組成した均等加重ポートフォリオが1月により高いリターンをえる観察を論文発表した1976年まで遡る。ちなみに，その理由は，均等加重ポートフォリオは時価加重ポートフォリオより，小型株の比重が高くなるからである。

その原因として，値下がりしている銘柄を12月には売り，1月に買い戻すという，税節約効果（Tax-Loss Selling Effects，Reinganum［6］1983年）と年末化粧効果（Window Dressing効果，Haugen-Lakonishok［3］1988年）以外に，小型株の低流動性が高プレミアムを生む効果（Reinganum［7］1990年）もあげられている。

Schwert［8］によると，米国ではその発見以来1月効果は継続し，効果は小さくなっているものの，1990年代も消滅していない。しかしながら，1月だけでなく他の月にも同様な現象が見られ，明瞭な結果をえていない研究もいくつかあるので，この点は論争中であると考えるべきであろう。しかも，小型株効果は消滅しているという計測もあり，1月効果の原因も不明になりつつある，ということになる。

なお，本稿は，日本のJASDAQ上場銘柄という小型株でも，既上場ではなく，そのIPOの1月効果を計測するという新しい視点をとっている。

3　データ処理方法

本稿では，JASDAQのIPO個別銘柄の初値乖離率を初取引日が属す月で分類する。なお，初取引日が公開価格決定日から月を越えるケースもありえるが，本稿では公開日＝初取引日＝初上場日のみに注目する。IPOが複数ある月では単純平均する。1996年1月から2003年12月まで最大96ヵ月分のデータをえる。そして，

（1）その月別初値乖離率推移を時系列グラフにする。IPOがない月は空白にする。

（2）96（IPOがない月は勘定に入れないので，その分サンプルの個数は減る）のデータを1月から12月までに分け，各月の平均と標準偏差などの諸統計量を計算して作図（横軸は1月から12月）する。

【250頁】

4　研究方法と結果

4-1　研究方法

他のデータとは特別かけ離れた値をとるデータは，特別な経済的理由があるからなのか，それとも測定誤差（measurement errors）などから生じた単なる外れ値（outliers，特異値とも言われる）なのか，判断しなければならない。特異データの処理方法としてはいくつか知られている（4。

しかしながら，本研究ではサンプル数が少なく，広く使われている外れ値処理方法は使えない。そのため，本稿では，日経ジャスダック平均のリターン，中位値，初値乖離率の標準偏差，スチューデント化したレンジ，プラスの件数―マイナスの件数，プラスの平均―マイナスの平均，の図を各年の1月から12月まで年別に描いた。

【251頁】

4-2　諸統計量の計測結果

（1）日経ジャスダック平均のリターン

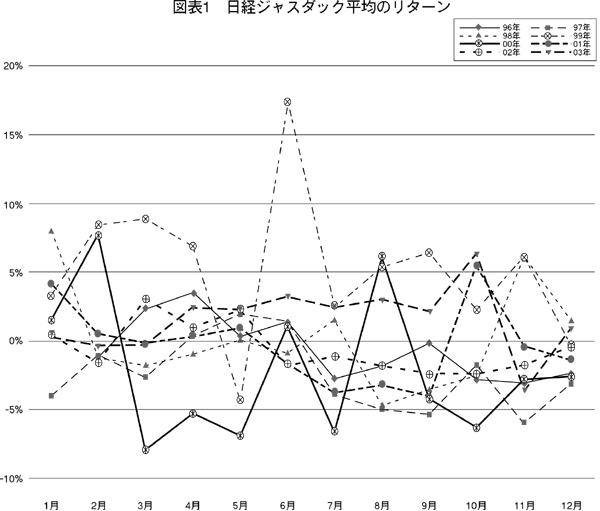
図表1に描いた日経ジャスダック平均のリターンは％表示で同指数の前月からの変化率の2分の1で計算したものである。つまり，日経ジャスダック平均リターン＝（当月日経ジャスダック平均終値−前月日経ジャスダック平均終値）÷2×前月日経ジャスダック平均終値。2分の1にするのは，公開から初取引日までのおよそ2週間で得れる（辰巳・桂山［11］参照）初値乖離率と時間間隔を合わせるためである。

図表を見ると月効果は明瞭ではない。さらに，市場全体の効果を除去するために，対市場初値乖離率超過リターン＝初値乖離率月次平均リターン―日経ジャスダック平均のリターン，についても，1月から12月までの同様な時系列図を図表2（252頁）に描いた。しかしながら月効果は明瞭ではない。

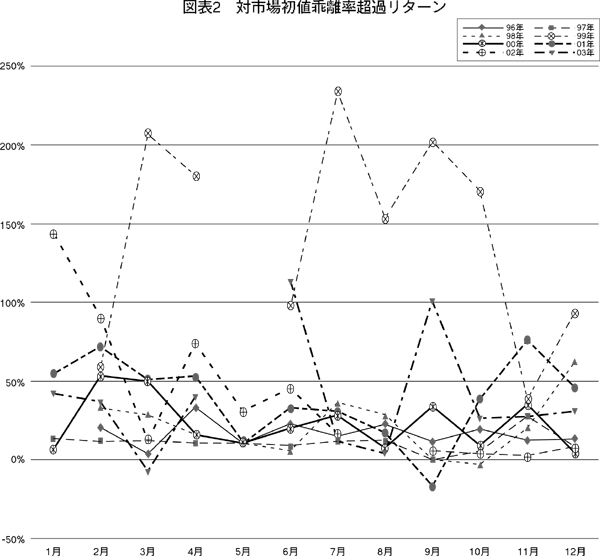
【252頁】

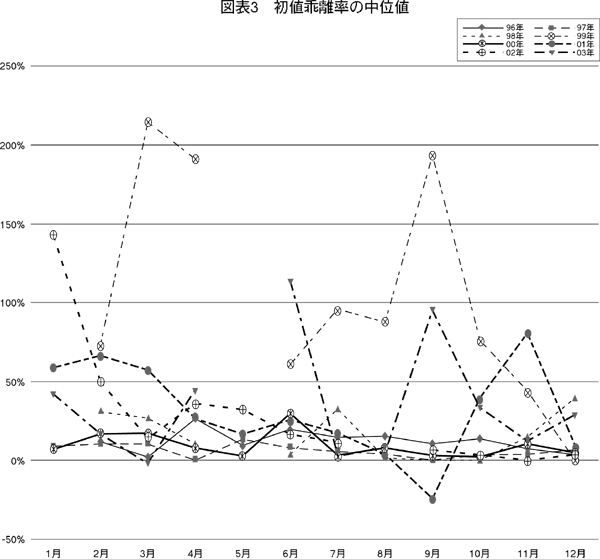
（2）中位値

中位値は，毎年何件かある，特別に高いあるいは低い（初値乖離率の）値の影響を除外する効果がある。IPO銘柄初値乖離率の中位値を図表3（253頁）に描いた。月効果は明瞭ではない。なお，公開会社数が1社しかない月は6件あるが，その値をそのまま入れてあるので，これらの月の中位値の意義はなくなっている。

（3）リスク

各月の初値乖離率の標準偏差を図表4（254頁）に描いた。5月とともに，1月の標準偏差は低いことがわかる。これは初値乖離率のばらつきが1月は少ないということでもある。なお，確かに月ごとの標準偏差は低いが，1月，5月は公開件数が極端に少なく，いずれも月間の公開社数が3件までで，ばらつきの少なさをいうには根拠不足である。

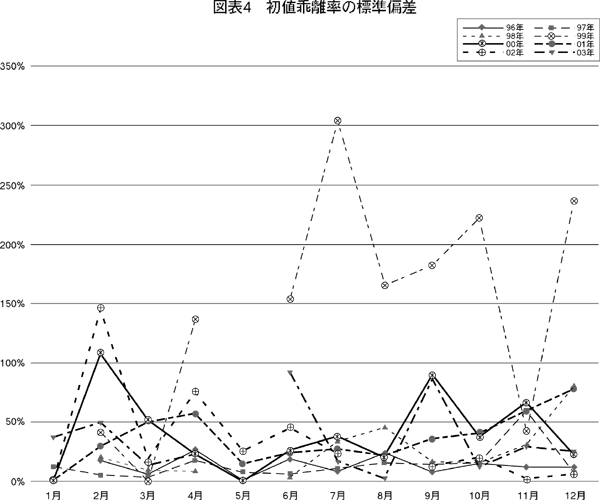
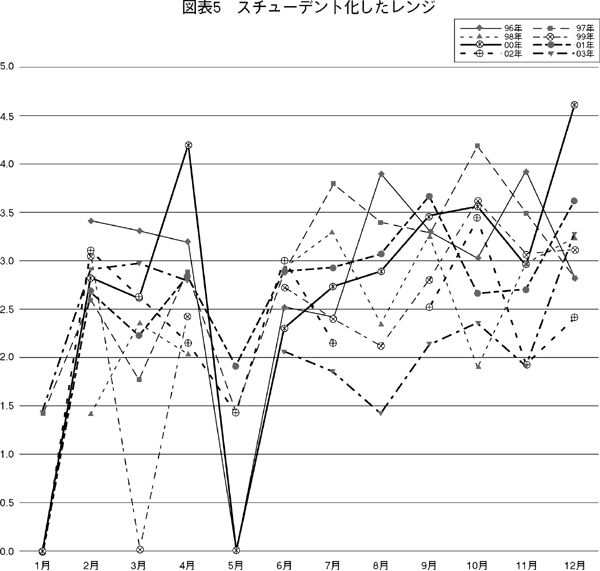
（4）スチューデント化したレンジ

最大値マイナス最小値のレンジを標準偏差で割るスチューデント化したレンジを図表5（255頁）に描いた。標準偏差がない時はデータを空欄にしている。レンジが大きいのは標準【253頁】偏差が高いからかもしれず，スチューデント化したレンジはその効果を除去している。

図をみれば，1月の規準化したレンジは低い，年前半も後半に比べて低い，ことがわかる。スチューデント化したレンジをリスクの指標と見る場合には，ハイリスク・ハイリターンの原則に反する。つまり，ハイリスク・ハイリターンの原則が成り立っておれば，1月はリスクが低く，リターンは低いことになるが，そうなっていなければアノマリーである。

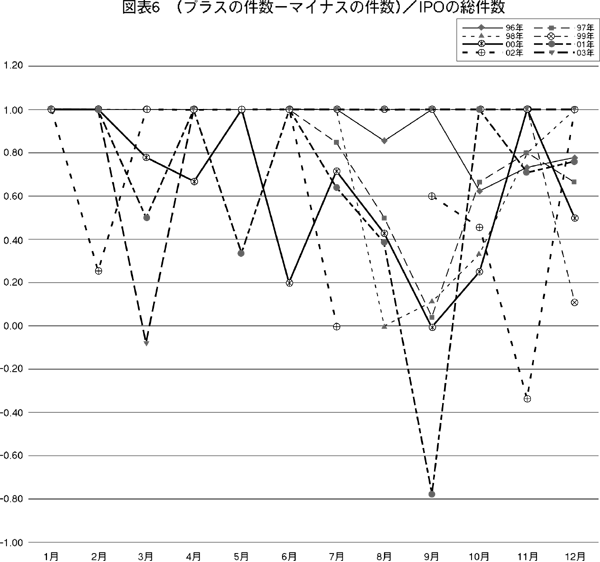
（5）初値乖離率がプラスのIPO件数―マイナスのIPO件数

（初値乖離率がプラスのIPO件数―初値乖離率がマイナスのIPO件数）をIPOの総件数で割って正規化した。つまり，（初値乖離率がプラスのIPO件数―初値乖離率がマイナスのIPO件数）／IPOの総件数を計算した指標を図表6（256頁）描いた。観察できるのは，1月は100％確実に初値乖離率がプラスであるが，他の月は必ずしもすべての年次でプラスになるわけではない。これを1月効果と呼べないことはない。

しかしながら，初値乖離率がプラスになっている場合の初値乖離率平均から初値乖離率がマイナスになっている場合の平均を差し引いてみる（図表は省略）と，月効果は明瞭ではない。ここで，「プラスの平均−マイナスの平均」は，「プラスの平均＋マイナスの平均（マイナス値）」【254頁】で計算している。

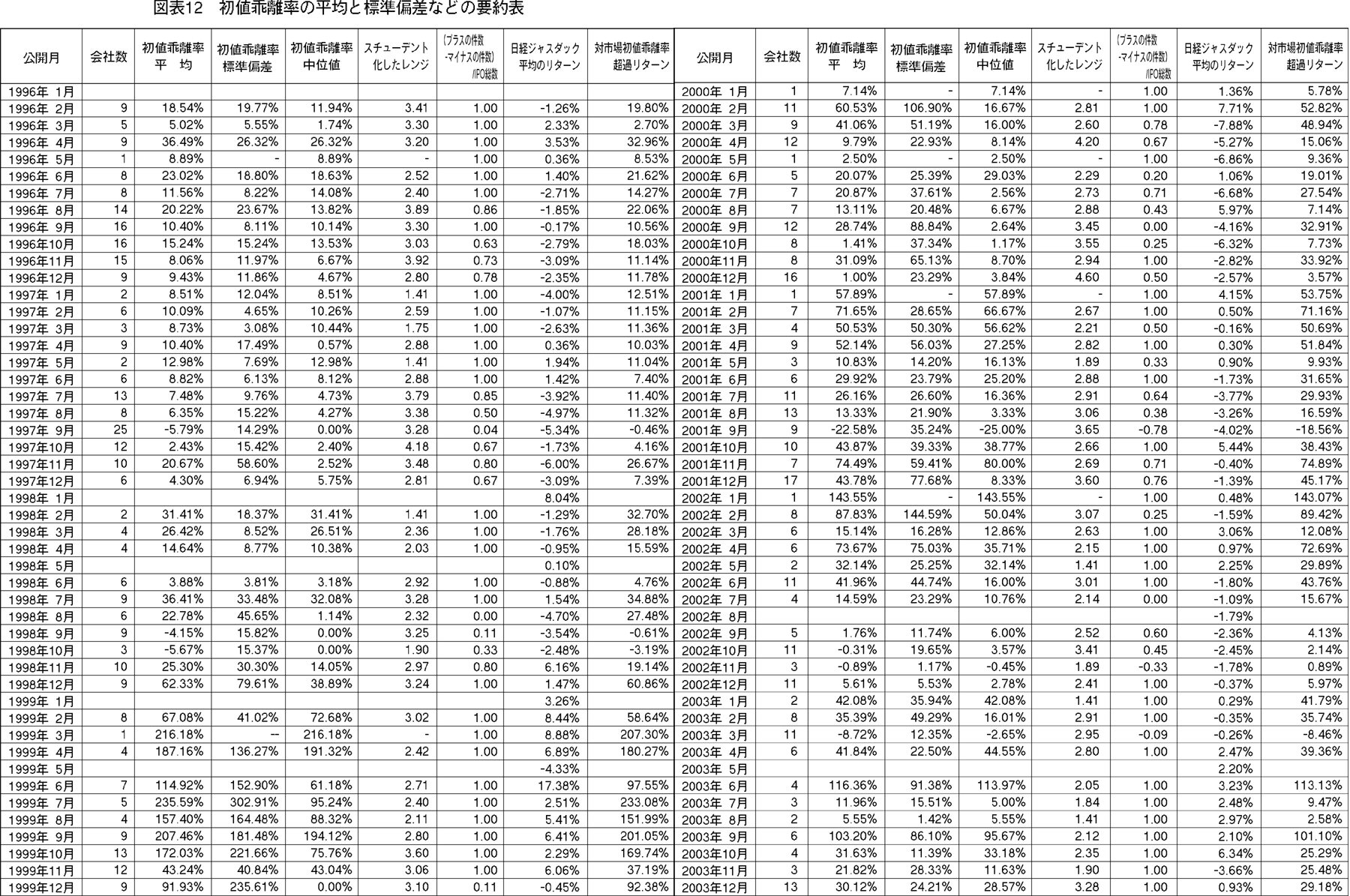
なお，各年各月の初値乖離率の平均と標準偏差などを巻末の図表12（262頁）に掲げた。

4-3　年初第一号銘柄の初値乖離率

さらに，年初第一号の銘柄名と初値乖離率を図表7（256頁）に挙げてみた。年初第一号のIPO銘柄の初値パフォーマンスは良い。2000年から2003年までの4年間で年初第一号銘柄は負けなしである。この間にはＩＴバブルによる株価の高騰とその後の崩壊があった。そのため1999年〜2000年にかけては，1月だけが高いのは説明がつかない。また，2001年〜2003年にかけては，株式市場全体の不調な動向とは関係なく，年初1月は好調になっている。

【256頁】

図表7　1996年以降の1月のIPO銘柄初値乖離率

注）各年の最初が年初第一号。2000年以降はJASDAQ以外を含めており，会社名あとのカッコ内に取引所を記した。2000年のムラチク：18.3％と2001年のクリード：326.7％は公開日が2月なので記入しなかった。

【257頁】

5　日経ジャスダック平均の曜日効果についての考察

5-1　曜日効果の特質

日経ジャスダック平均（5の日終値データ（1989年1月から2003年8月まで）について，前日終値から当日終値までの変化率を計算すると，月曜日は平均と標準偏差が低い。

さらに，火曜日終値から水曜日終値までの変化率の推移については，他の曜日や同様に分析した日経平均とは違う複雑な非線形特性が現れている（宮野・辰巳［4］［5］）。

非線形な複雑さと呼ばれるのは，本ケースを具体例に説明すると，水曜日毎の時系列リターン・データを作り，サンプルの様々な小期間をとってみると，ある小期間で観察された変動パターンが時間を進めた別の小期間で同様な変動パターンが，他のどの曜日と比較しても，観察されないということである。

それは，水曜日のリターンの平均値の高さ，標準偏差や歪度・尖度のいずれにも見られない，特異な動きである。これをどう解釈するべきだろうか。何によって生じているのであろうか。1つの可能性を指摘しておこう。

5-2　公開日の曜日分布

1989年以降新規公開企業数がそれ以前と比較すると増えてきており，特にJASDAQ市場等の新興市場といわれる市場については新規公開株に値動きが集中する可能性が指摘できる。そして，新規公開については，払い込み期日の翌日が上場日となるため，一般的に火曜日以降の曜日が上場日になることが多い。

この点が大きな影響力を持っているのではないかと考えられる。それを検証するためには，次の3点を確認する必要がある。（1）IPOは90年代後半以降，それ以前と違い，急増している。（2）日経ジャスダック平均はIPO価格を逐次反映している。（3）IPOの初取引は水曜日に多くなされている可能性がある。特に，この最後の点を確認するためには，IPO初取引日の曜日分布，月曜日から金曜日までの件数分布を96年以降計算する必要がある。

まず，第一の点はすでに様々なところで明らかにされており，改めて説明するまでもない。また，第二の点の，日経ジャスダック平均はIPO銘柄の初取引日の高価格の影響を受けやすいという事実はあるのだろうか。それは，日経ジャスダック平均の採用株価方針（ストップ高など，採用）から明らかにできる。また，追加銘柄は値が付いた翌営業日から算出対象になる，事実も影響している。

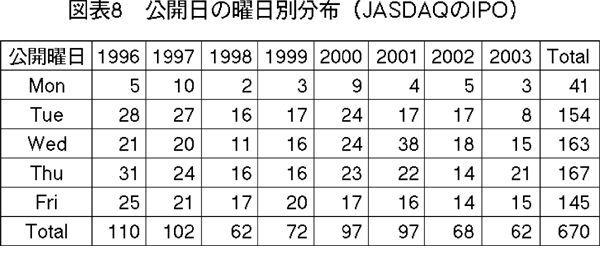
第三の点を明らかにするために，個別銘柄データから1996年から2003年までの公開日＝初取引日の曜日を調べ，月曜日から金曜日のIPO件数累計を計算して図表8に要約にした。

月曜日の公開は，8年間で全体の6.1％に過ぎず，大変少ない。水，木曜日にピークがある。

上場日件数は月曜日から火曜日の増加が著しく大きい。この変化は，IPO銘柄が日経ジャスダック平均に採用される翌日に持ち越され，火曜日から水曜日の株価変化になって現れている【258頁】ものと予想される。日経ジャスダック平均の曜日アノマリーにこの要因がどれ位影響しているかは現時点でわからないが，その原因の1つとしてさらに解明するべきポイントはこのあたりにあるものと予想されるのである。

ちなみに上場日件数の大きな減少が株価変化に現れるのは，同じ論理で捉えると，月曜日から火曜日である。しかしながら，IPO銘柄上場数の減少は既上場銘柄の影響が大きくなるということであり，IPOの影響が小さくなり，初値の著しい高騰と日経ジャスダック平均の動きとの係わりは小さい。

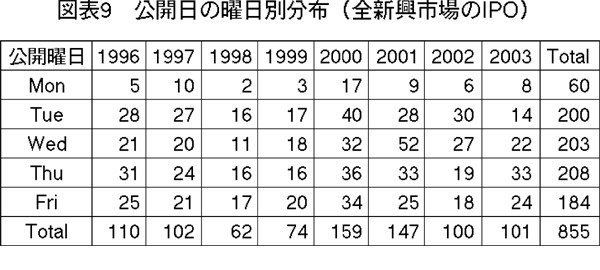
さらに，次の図表9は，JASDAQだけに限定せず，1999年末からのNASDAQ JAPAN（大証ヘラクレス），東証マザーズ（6なども含めた表である。月曜日の公開は8年間で7.0％に過ぎず，同じような結果になっているのは，新興株式市場の上場申請手続き上の理由から，月曜日の上場は少なくなる，ということである。

5-3　その他の考察

IPO価格の高騰が日経ジャスダック平均に影響を与えているのかという点に関しては，どちらかというと，ふつう逆の印象をもたれている。前節では，日経ジャスダック平均には都度IPO銘柄が加わり，そのため，日経ジャスダック平均の推移が曜日によって変な動きになっている，というテクニカルな要因を指摘した過ぎない（7。株価ブームと同時あるいはそれに少し遅れてIPOブームがある，あるいは，日経ジャスダック平均株価で現れる市場環境の変化が，IPO銘柄の高騰・下落に影響している，という現象とは矛盾しない。

【259頁】

6　まとめ

さて，IPO1月効果の理由は何だろうか。いくつか考えられる点を指摘して，稿を終えたい。

まずJASDAQの株主構造が及ぼしている効果に注目しておかなければならないだろう。JASDAQ上場企業（店頭管理銘柄や日本銀行を除く）のうち2003年度中に決算期を迎えた会社を対象にした2004年3月末株式分布状況調査によると，総株式数に占める個人の持ち株比率は49.9％，金額保有比率は50.7％とほぼ半数，他方金融機関（生・損保を含む）の持ち株比率は9.0％，外国人投資家についてはそれぞれ11.0％，10.3％だった。

それは，IPOに参加できない，流動性が低いためシステム運用がしづらい，などの理由のためであろう。それゆえ，初値形成には機関投資家は係わっていない。そのため，アノマリー論議で指摘される，機関投資家のポートフォリオの年末化粧（損失の出ている銘柄を売却する。税も節約できる）と1月の買戻しが大きな原因であるとは考えられない。

主幹事証券会社の，年初の公開価格を低めに設定する，御祝儀相場形成誘因が次に考えられる。これは否定できない。しかしながら，このような現象に対する検証の方法は現在のところ知られていない。

第三に，個人投資家の態度と行動が原因となることも考えられる。例えば，年末休日と正月3賀日の間に一斉にお休みしたIPO資金が年初第一号IPO銘柄に集中するとしたら，大きな株価上昇圧力になるだろう。

参考文献

［1］Bandt, C. and Pompe, B., "Permutation Entropy: A Natural Complexity Measure for Time Series", Phys. Rev. Lett., vol.88, pp.174102-1〜174102-4, 2002.

［2］Chien, C-C., Lee, C-f. and Wang, A. M. L., "A note on stock market seasonality: The impact of stock price volatility on the application of dummy variable regression model", Quarterly Rev. of Economics and Finance, vol.42, pp.155-162, 2002.

［3］Haugen, R. A. and Lakonishok, J., The Incredible January Effect, Dow Jones-Irwin, 1988.

［4］宮野尚哉・辰巳憲一「非線形時系列解析による株価の曜日効果分析」，学習院大学経済経営研究所ディスカッション・ペ−パ−No.03-3，2004年2月，P. 12。

［5］宮野尚哉・辰巳憲一「非線形時系列解析による株価の曜日効果分析」，『電子情報通信学会論文誌Ａ』，Vol.J87-A, No.9，2004年9月，pp.1226-1235。

［6］Reinganum, M. R., "The Anomalous Stock Market Behavior of Small Firms in January: Empirical Tests for Tax-Loss Selling Effects", Journal of Financial Economics,1983,12, pp.89-104.

［7］Reinganum, M. R., "Market Microstructure and Asset Pricing: An Empirical Investigation of NYSE and NASDAQ Securities", Journal of Financial Economics,1990, 28, pp.127-147.

［8］Schwert, G. W., "Anomalies and Market Efficiency", in Constantinedes, G., Harris, M. and Stultz, R. M. (eds.), Handbook of the Economics and Finance, North-Holland, 2001.

［9］辰巳憲一・金チュル印「株式売買制度のパフォ−マンス」『学習院大学経済論集』，1997年4月，pp.11-28。

【260頁】［10］辰巳憲一・桂山靖代「小売業企業の店頭公開後株価パフォーマンスとリスク」『学習院大学経済論集』2002年1月，pp. 115-146。

［11］辰巳憲一・桂山靖代「わが国店頭株式市場の公開価格決定におけるブックビルディング方式〜統計分析による入札方式との比較〜」『証券経済研究』41巻（2003年3月）， pp.143-157。

［12］辰巳憲一・桂山靖代「オーナー会社や子会社の株式公開〜企業形態などが初値乖離率やIPO後株価パフォーマンスなどに及ぼす影響の統計分析〜」『証券経済研究』47巻（2004年9月），pp.65-82。

［13］辰巳憲一・桂山靖代「新規株式公開売り出しとその収益性〜囲い込み仮説などの検証〜」2004年7月。

［14］Tong, W., "International Evidence on Weekend Anomalies", Journal of Financial Research, Vol. 23, No.4, Winter 2000, pp.495-522.

［15］Wayland, R., Bromley, D., Pickett, D. and Passamante, A., "Recognizing Determinism in a Time Series", Physical Review Letters, Vol. 70, No.5, February 1993, pp.580-582.

巻末付録

平成不況にあたり，株式市場の低迷によって，IPO人気が高く，ＢＢ（ブックビルディング（8）の抽選倍率は高くなっている。その結果，多くの個人投資家にとって重要なことは，初値ではなく，初値以降の流通市場株価の動きはどうかということになる。図表7に示した2000年から2003年の12銘柄のうち，年末の株価が初値以上であったのは3銘柄だけだった。

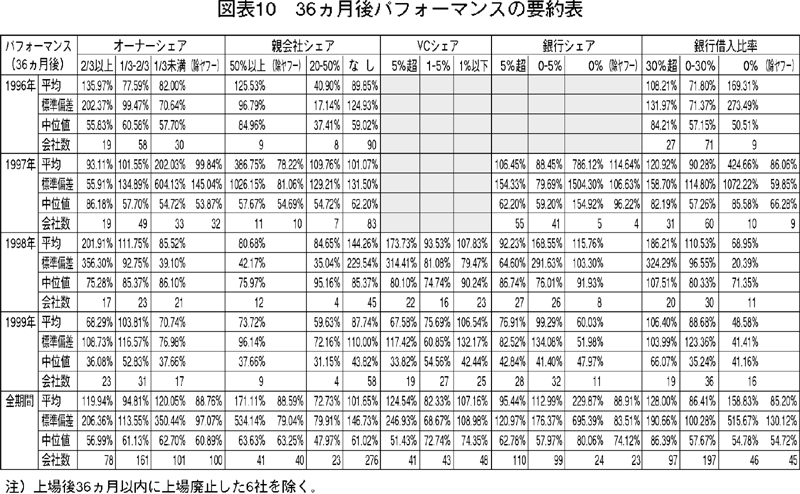
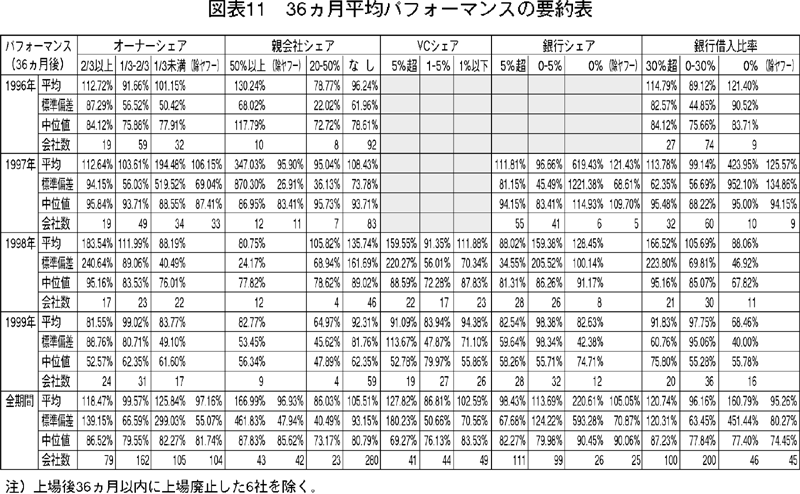
上場後1ヵ年のパフォーマンスが悪い事実は，一般に，公開月に依存しない。しかしながら，さらに長期の36ヵ月後までになると必ずしもすべての企業や株主に妥当しない。株主によってパフォーマンスは違う。1996年から1999年までにJASDAQに公開した全社の株主主体別36ヵ月後と36ヵ月平均株価パフォーマンスの要約表を次の図表10と図表11に掲載した。詳細な説明と分析は辰巳・桂山［12］を参照のこと。

36ヵ月後パフォーマンスは，各銘柄の公開日が属する月の末日の株価を当該月末の日経ジャスダック平均で除したものを100％とした相対株価に対して，公開後36ヵ月後の月末のパフォーマンスを算出したもので，36ヵ月後月末株価を公開月末株価で除した指数を，同様に当該36ヵ月後月末日経ジャスダック平均を当該公開月末日経ジャスダック平均で除した指数で除したものである。なお，株価は株式分割の調整済みを採用している。

また，36ヵ月平均パフォーマンスは，上記と同様に市場調整をして，公開月末から36ヵ月後まで1ヵ月単位で月末の指数を算出し，その銘柄毎の各月指数の単純平均を算出したものである。

レベルの高さは，100％を基準に考えるべきで，100％を下れば市場平均を下回ることを意味している。