【27頁】

経済数学における概念の数式表現のための知識データベース構築

白田　由香利†

要旨

本稿では，学部レベルの経済数学で必要とされる，(a) 連立方程式の経済学への応用，(b) 経済学における導関数の用法，(c) 経済学における多変数関数の計算の3分野について，その分野の問題の解法に必要とされる用語及び概念の数式すべてを，Prologのルールとして表現し，学部レベルの経済数学問題の解法に必要な知識ベースを構築した。これにより，問題として与えられたデータ以外の式を導出し，必要な数の方程式を揃えることが可能となり，与えられた経済数学問題に対して，経済の領域知識を用いて正しい問題解決過程を求めることが可能となる。

１．始めに

本稿では，従来からデータベースの分野と人工知能の境界領域の研究として注目を集めている知識データベースの構築を，経済数学に出現する概念及び用語の数式表現を対象として行なった結果を報告する。我々は経済数学に関するITS（Intelligent Tutoring System）の研究開発を行なっているが，このITSを構築する場合，経済数学に関する知識データベースの構築が必要となってくる。まず我々が想定するITSに求められる機能であるが、以下の2つがある。

(1) 与えられた経済数学問題に対して，経済の領域知識を用いて正しい問題解決過程を求める。

(2) 問題解決過程において言葉やグラフ，アニメーションなどを用いて学習者の質問に答える。

本論文では上記(1)を，証明問題を除く決定問題に限定した場合を考える＊。つまり与えられた経済数学問題の中心的部分には，必ず連立方程式が在る。そして問題解決のためには，まず必要な連立方程式をセットアップする必要がある。与えられた文章中には，連立方程式を作成するために必要なデータや条件が記述されているが，一部のデータや条件は経済の基本的知識として記述が省力されている場合がある。学習者がそうした経済数学の基本的知識に気がつかない場合あるいは元々知らない場合，ITSは学習者支援のために学習者に代わってその知識を【28頁】もつ必要がある。この経済数学の基本的知識をどのように知識ベース化するかが本論文の主題である。

我々は学部レベルの経済数学で必要とされる，(a) 連立方程式の経済学への応用，(b) 経済学における導関数の用法，(c) 経済学における多変数関数の計算の3分野について，その内容を調べ，その分野の問題の解法に必要とされる用語及び概念の数式すべてを，Prologのルールとして表現し，経済数学問題の解法に必要な知識ベースを構築した。参考とした経済数学のテキストは，Dowlingの経済数学の入門書であり，広く普及しているテキストである１。また，必要となる用語及び概念を網羅するために，GREの問題集２の用語集，及び他のDowlingの著作となるテキスト３,４，及び広く利用されている経済数学テキスト５を参照した。

ITSとしての一般的，解決可能な問題の範囲についての議論は，人工知能のCAIの分野で広く研究されている。この分野のサーベイとしては，例えば，大槻らの論文が参考となるであろう６。本論文の主題は，そうしたCAIシステムの限界的能力を対象とするものではない。また，限定分野に対してわずかの初期知識から新しい知識を発見するというような，発見システム†の開発でもなく，本稿の目的は，経済数学向けe-Learningシステムにおいていかに数学知識を表現するかという問題に対して我々の採った現実的アプローチを説明するものである。データベースにおける知識獲得についての汎用技術は，西尾の論文などを参考として頂きたい７。

２．知識の分類

本節では，経済数学問題を解く場合必要となる数学表現知識が3種類あることを示し，そのうちのどの部分を知識ベース化するのかを示す。

一般的に数学問題では，その問題（文章題）中に与えられるデータの他，数学公式およびその分野に特化する知識（セオリー）がある。我々が研究開発したe-Math Interaction Agentにおいては，前者は，メタレベル記述ファイルという問題定義ファイルで与えられる８。こちらは個々の文章題に特化したデータである。他方，後者にあたる知識は一般性が高くなる。経済数【29頁】学の場合，経済に特化する知識が後者のセオリーに当たる。この他，数学問題の解法プラン，あるいは問題解決過程の知識が必要となる。例えば，最大値を求める数学的手法がこれに相当する。一般に解法プランはアルゴリズムとして定義される。我々のe-Math Interaction Agentでは，解法プランは予め問題のタイプごとに定義する。

まとめると以下の3種類に知識は分類される。

(1) 経済に関する知識

(2) 個々の問題に特化して与えられるデータ

(3) 問題タイプに対する解法プラン

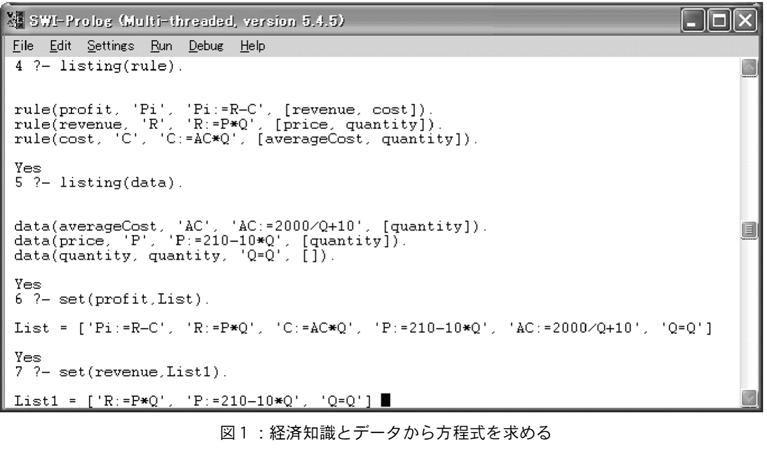
問題に対して連立方程式を立てる際，(1)及び(2)の知識及びデータが必要となる。その導出をPrologで行っている様子を図1に示す。ここでは経済知識として，profit, revenue, costの知識表現が定義されている。またこの問題として与えられたデータとして average cost, priceの式が与えられている。知識はrule，与えられたデータはdataで定義されている。両者とも，第1引数である変数を定義するための引数セット及び，その変数間の関係式を定義している。例えばrevenueは引数price及びquantityで定義されていることがルールとして表現されている。

この問題の未知数をprofitとした場合，set()を起動することで，Prologでユニフィケーションを行い，結果の連立方程式 π(R,C), R(P,Q), C(AC,Q), P(Q), AC(Q) を求めてListに入れている。data (quantity) はそれ自体他の変数で定義されていないので，つまりそれを定義する引数が空リストなので，ここで検索が止まる。この検索エンジンでは，このように独立変数として残したい変数をdataとして追加しておく必要がある。

必要な連立方程式が一旦求められた後は，数式処理システムによって記号により方程式を解【30頁】くことが可能である。従来のITSの多くは開発システム中にPrologの数式処理システムを内包することが求められたが，現在のように数式処理システムが容易に起動可能となった状況では，必要に応じて数式処理システムのsolve関数を呼び出すほうがシステム構築は効率良く行えると考える。MapleT.A.というシステムでは，学習者が入力した数式が,教師が想定した数式と，syntactical equalであるか否かのチェックを行うため，Mapleを起動して計算をするような機能がある。このように必要な数式処理はその都度数式処理システムを起動する，という方式が実現可能な時代となったと言える。

上記の問題においても，Mapleシステムのsolve関数によりprofitをquantity Qの関数として求めることが可能である。Prologシステムの役割は，経済知識を用いて必要な数の連立方程式を正しく求めることである。

３．方程式セットアップのための要件

与えられた経済問題に対して連立方程式を立てるためには，必要な数の方程式を知識ベースから発見し，未知数を指定の変数で表現可能とする必要がある。そのための関数としてset()を作成した。関数setは，指定の未知数（unknown）を，指定の引数リスト（paramList）のみで表現可能な連立方程式に展開する。結果の連立方程式はresultListに入る。

・set(unknown, paramList, resultList)

【31頁】但し，未知数は引数リストの全ての変数を含む必要がある‡。この条件が満たされないと関心のある知識表現にマッチしない場合があるからである。

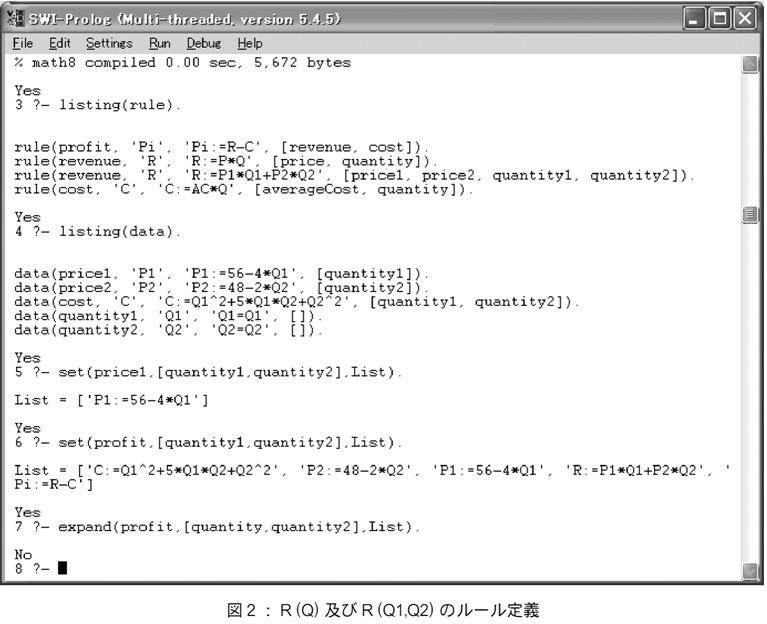
収入revenueの計算の場合，商品が2種類ある場合，R=P1*Q1+P2*Q2と表現される。経済知識ベースを構築する場合，関心のある引数リストごとに同じrevenueに対して複数の数式表現を格納しておく必要がある。図2のルールではrevenueに対して２つのルールが定義されている。Profitをquantity1及び2で展開しようとした場合，図2のようにデータを与えると，問合せは

set(profit, [quantity1,quantity2], List)

となり，結果として，以下のように5本の方程式が得られる。

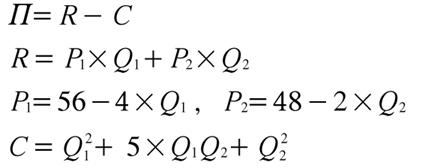
これによりπ(Q1,Q2) の式が求められる。図2の最後に示されたsetによる問合せは，profitを[quantity, quantity2]という間違った引数セットで展開しようとすると失敗する，ことを示している。

経済数学用知識ベース構築にあたり注意すべき点は，必要な使用頻度の高い数式表現を変数名が衝突しないように，複数の引数セットで表現することである。以下の章では，それぞれの分野ごとにどのような知識表現をルール化したか，また実際の経済数学問題との対応を，例をあげて示す。知識ベース化された経済知識は35個でありそれらは付録として添付したので，参照して頂きたい。

４．連立方程式の経済学への応用

【32頁】

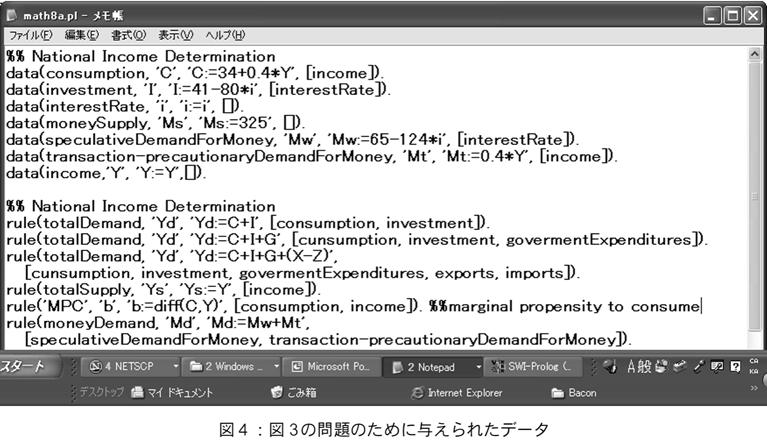
【33頁】まず連立方程式を立てるための経済知識としてどのようなルールを定義したかを説明する。経済数学の連立方程式に関する問題の主たるテーマとして国民所得決定問題があり，ルールとして図4に示すような2セクター，3セクター，輸入輸出まで入れた総需要の３モデルを定義した。データとして図4のdataが与えられた場合，CとIしか定義されていないため，モデルは2セクターモデルが選択される。その他のモデルが選択された場合，必要な変数が見つからないためエラーとなりその検索は終了する。例えば，Gなどはdataとして定義されていないためエラーとなり，そこで検索が止まる。

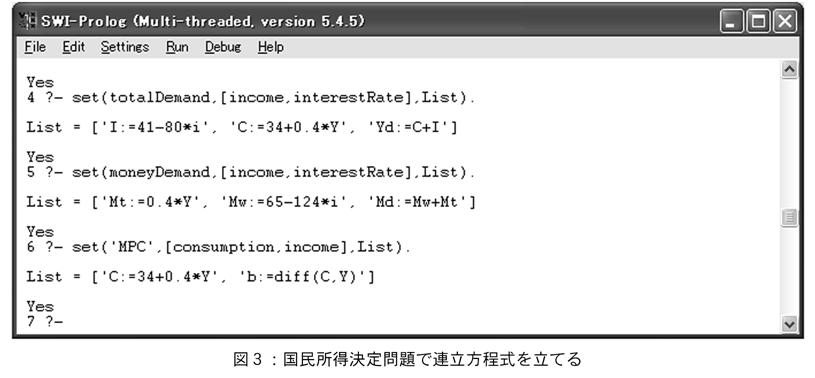
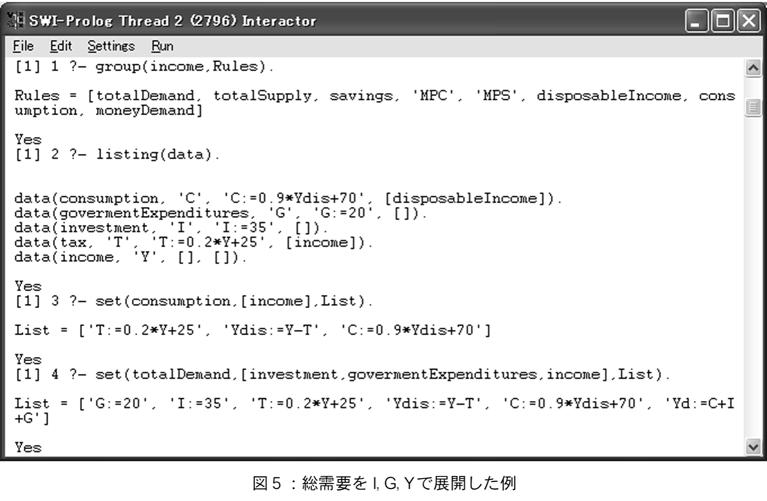
図3の例では，総需要，及び貨幣需要の変数を，引数［国民所得Y，利率i］で展開した様子を示した。結果は正しく2セクターモデルYd=C+Iが選択された様子を示している。また貨幣需要も正しく展開されたことが示されている（図3参照）。

図3の3番目の例はMPCを引数C及びYで展開しようとした問題である。結果として問題として与えられたCの方程式C(Y)　及び，MPCの定義式が検索により得られた。MPCの知識ルールでは記号bを使って関係を定義しているので，このような結果となる。Prologのユニフィケーションでは，単に定義された関係式を返り値として返すだけなので，自由な記号を使って式が表現可能である。ここでdiffはMapleの表現で微分及び偏微分を意味する。Diffでは第１引数を第2引数により微分する。このset関数の返り値である方程式をMapleに渡せば，具体的な計算がそのまま実行できるように，このようなdiff表現を用いた。

図５の例は，総需要をI,G,Yで展開した例を示した。ここでは，与えられたCが間接的に税Tを含むため，Ydis=Y−Tの式が結果に含まれる。この展開においても総需要は正しく3セクターモデルを選択していることが確認された。

５．経済学における導関数の用法

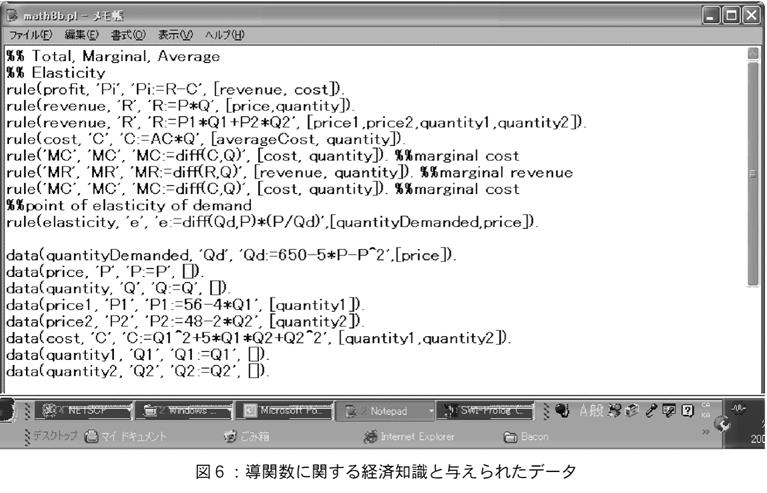
【34頁】次に経済における導関数の用法の分野を説明する。この分野では主に最適化問題と価格弾力性の定義を行った（図6参照）。式はMapleを使うことにより，ある変数について解くことが可能である。例えば需要関数をデータとして与える際，式としては陰関数の形で表現することも可能であり，変数の表現形式は解が定まる限り問わないからである。また式がPで与えられていた場合，逆関数Qを求めるなどの操作も，Mapleに任せるべき作業であり，経済知識としては，関係式のみを定義すればよい。

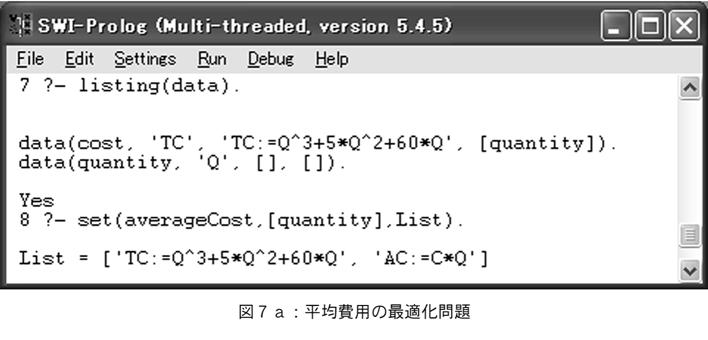
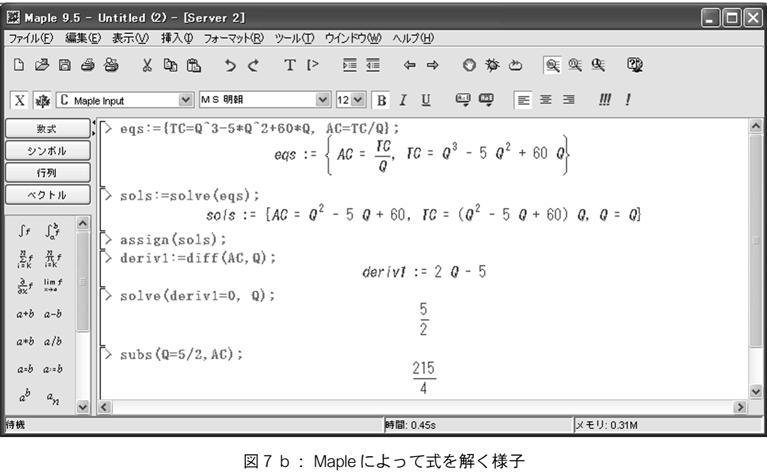
【35頁】次に，平均費用を最小化する点を求める最適化問題を解く場合を考える。文章題で総費用関数が与えられるとする。あとひとつ必要な式は平均費用の定義式である。これはルールとして定義されている。問合せ set(averageCost, [quantity],List) によって，ACがQの関数として展開される（図7ａ参照）。得られた2式は，AC(Q)を計算するためにMapleに渡される。図7ｂにMapleで処理される計算の過程を示した。この命令の与え方は人間が対話的に入力する方式であるが，同様の過程を予め定義されている解法プランに従いシステムが行うようにシステムを構成することが可能である（実際には2階微分を計算して，得られた極小値が最小値であることを証明する必要があるが，ここでは省略している）。

需要の所得弾力性に関する式の展開例を次に見てみよう（図8参照）。

はじめに需要の式をデータとして与える。問合せとしてset (elasticity,...) を与えると，結果として図8の2式が返る。第1式は与えられた需要の式であり，第2式は，所得弾力性の定義式である。

６．経済学における多変数関数の計算

【36頁】

本節では経済における多変数関数の計算に関する知識の定義を説明する。

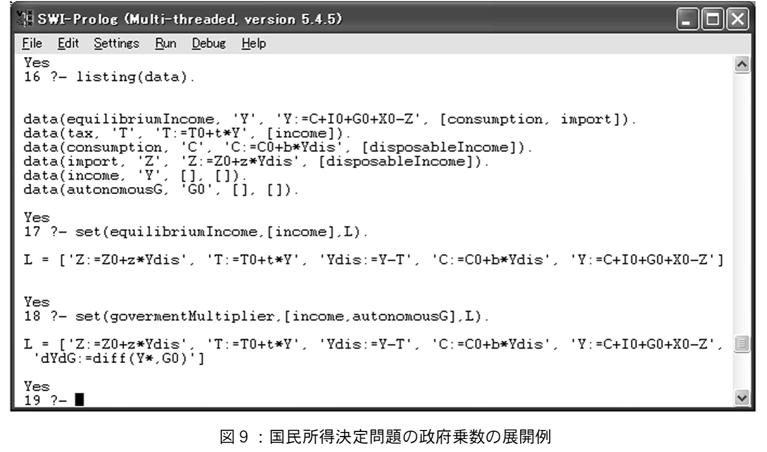
多変数関数の問題の多くは，前章で述べた最適化問題の多変数化である。Mapleではdiffで偏微分も表現できるので，多変数化によって加える必要のある知識は，revenueなどの変数のみであり，微分に関する定義に変更をする必要はない。また図9に示したような国民所得決定問題における各種の乗数の定義をルール化した（付録参照）。

多変数関数に関する問題としてラグランジェの未定乗数法がある。ラグランジェ式を知識として入れるべきか考えた結果，この定義式は解法プランに属するものであるとし，経済知識ルールには入れないこととした。あくまでも知識を，経済知識ルール，与えられたデータ，解法プランの3つに類別し，それぞれの独立性を高めたほうがシステムの寿命が長くなるからである。

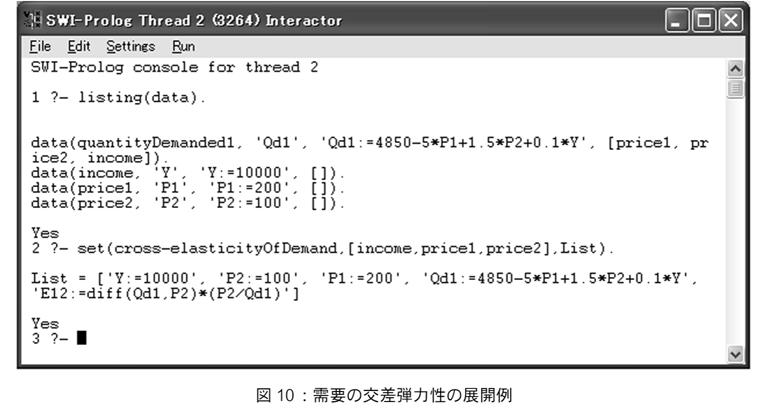
需要の交差弾力性，価格弾力性などの定義も経済知識ルールとして入れた。図10では需要関数式および，所得，2財の価格式を与え，その需要の交差弾力性の式を求める展開を行った。変数が5個，式が5本得られたので，これはMapleのsolveで解くことが可能である。

７．まとめ

本稿では，学部レベルの経済数学で必要とされる，(a) 連立方程式の経済学への応用，(b) 経済学における導関数の用法，(c) 経済学における多変数関数の計算の3分野について，その分野の問題の解法に必要とされる用語及び概念の数式すべてを，Prologのルールとして表現し，経済数学問題の解法に必要な知識ベースを構築した。こうした知識データベース及びPrologエンジンによって，問題として与えられたデータ以外の式を導出し，必要な数の方程式を揃えるこ【37頁】とが可能となる。方程式を解くことはMapleのsolve関数を呼び出すことで可能となる。これにより，与えられた経済数学問題に対して，経済の領域知識を用いて正しい問題解決過程を求めることが可能となる。

定義した経済知識ルールは35個であった。この35ルールの拡張として，国民所得決定問題の各種の乗数定義を追加するなどが考えられるが，この35のルールの組合せで正しく知識が表現できていることを確認できた。その確認のため，代表的な経済数学問題をデータとして与え，式の展開が正しく行えることを確認した。この知識ルールは入れ替える必要はない。

数学用Web教材システム生成システムを研究開発してきた経験から得られた重要なことは，必要な知識を3つのグループ，(1) 経済知識，(2) 文章題で与えられたデータ，(3) 問題タイプに対する解法プラン，に分けることであった。これらを独立化することにより夫々の知識の独立性を向上させ，そのデータベースを独立に拡充することが可能となる。(2) のデータに関しても，ドリル問題を多数データベース化するという目的のため，独立化することは重要である。経済知識データベース及び，解法プランのデータベースの充実ももちろん今後一層行われるべきものと考える。

Prologによる知識データベースへの問合せ機能，及びMapleによる方程式の解法機能を適宜起動することで，既存の数学に関するITS及びe-Learningシステムの機能はさらに向上し学習者の学習を支援するものと考える。どのような組み合わせが有効であるのか，今後とも研究を重ねていきたい。

謝辞　本研究の一部は，平成17年度科研費基盤研究(C)(2)「マルチメディア教育支援システムeMathにおける教育用データベースの構築」（課題番号：15606014，代表：白田由香利）による。ここに記して謝意を表します。

付録

%% Optimization

%% Total, Average, Marginal

・rule(profit, 'Pi', 'Pi:=R-C', [revenue, cost]).

・rule(revenue, 'R', 'R:=P*Q', [price, quantity]).

・rule(revenue, 'R', 'R:=P1*Q1+P2*Q2', [price1, price2, quantity1, quantity2]).

・rule(cost, 'C', 'C:=AC*Q', [averageCost, quantity]).

・rule('MC', 'MC', 'MC:=diff(C,Q)', [cost, quantity]).

・rule('MR', 'MR', 'MR:=diff(R,Q)', [revenue, quantity]).

・rule('MC', 'MC', 'MC:=diff(C,Q)', [cost, quantity]).

・rule('MPk', 'MPk', 'MPk:=diff(Q,K)', [quantity, capital]).

・rule('MPPk', 'MPPk', 'MPPk:=diff(Q,K)', [quantity, capital]).

・rule('MPl', 'MPl', 'MPl:=diff(Q,L)', [quantity, labor]).

・rule('MPPl', 'MPPl', 'MPPl:=diff(Q,L)', [quantity, labor]).

・rule('MRP', 'MRP', 'MRP:=MR*MP', ['MR', 'MP']).

【38頁】・rule('MRTS', 'MRTS', 'MRTS:=diff(K,L)', [capital, labor]).

　%% Elasticity

・rule(price-elasticityOfDemand, 'Ep', 'Ep:=diff(Qd,P)*(P/Qd)', [quantityDemanded, price]).

・rule(price-elasticityOfSupply, 'Es', 'Es:=diff(Qs,P)*(P/Qs)', [quantitySupplied, price]).

・rule(income-elasticityOfDemand, 'Ey', 'Ey:=diff(Qd,Y)*(Y/Qd)', [income, quantityDemanded]).

・rule(cross-elasticityOfDemand, 'E12', 'E12:=diff(Qd1,P2)*(P2/Qd1)', [quantityDemanded1, price2]).

%% National Income Determination

・rule(totalDemand, 'Yd', 'Yd:=C+I', [consumption, investment]).

・rule(totalDemand, 'Yd', 'Yd:=C+I+G', [consumption, investment, govermentExpenditures]).

・rule(totalDemand, 'Yd', 'Yd:=C+I+G+(X-Z)', [consumption, investment, govermentExpenditures, exports, imports]).

・rule(govermentMultiplier, 'dYdG', 'dYdG:=diff(Y*,G0)', [equilibriumIncome, autonomousG]).

・rule(importMultiplier, 'dYdZ', 'dYdZ:=diff(Y*,Z0)', [equilibriumIncome, autonomousZ]).

・rule(exportMultiplier, 'dYdX', 'dYdX:=diff(Y*,X0)', [equilibriumIncome, autonomousX]).

・rule(taxationMultiplier, 'dYdT', 'dYdT:=diff(Y*,T0)', [equilibriumIncome, autonomousT]).

・rule(totalSupply, 'Ys', 'Ys:=Y', [income]).

・rule(savings, 'S', 'S:=Y-C', [income, consumption]).

・rule('MPC', 'b', 'b:=diff(C,Y)', [consumption, income]).

・rule('APC', 'APC', 'APC:=C/Y', [consumption, income]).

・rule('MPS', 'a', 'a:=diff(S,Y)', [savings, income]).

・rule('APS', 'APS', 'APS:=S/Y', [savings, income]).

・rule('MPS', 'a', 'a:=1-b', ['MPC']).

・rule(disposableIncome, 'Ydis', 'Ydis:=Y-T', [income, tax]).

・rule(consumption, 'C', 'C:=a*Y+b', [autonomousConsumption, 'MPC', income]).

・rule(consumption, 'C', 'C:=a*Ydis+b', [autonomousConsumption, 'MPC', disposableIncome]).

・rule(moneyDemand, 'Md', 'Md:=Mw+Mt', [speculativeDemandForMoney, transaction-precautionaryDemandForMoney]).