�W�c�I��������T�[�r�X�ɂ�����������ݕ⏕�̖���
�����x�C�Y�m���ƃi�b�V�������ɂ�镪��
�암�@�ߕF
�����̓��퐶�����Ƃ̐��Y�����̓C���t���X�g���N�`���A�i�C���t���Ɨ����j���邢�͎Љ�I���ʎ��{�ƌĂ�鋤�ʊ�ՂɈˑ����Ă��邱�Ƃ͌����܂ł��Ȃ��B�����������ɏ���҂��Ƃ��C���t����L���Ɋ��p���邽�߂ɂ́C�����̃}�b�`���O���X���[�Y�ɂȂ����悤�ȃC���t�������ƍX�V�Ƃ��Ȃ���Ă��Ȃ���Ȃ�Ȃ��B�Ⴆ�Γd���͕K���i�̈�����C���z�d����R���Z���g���Ȃ���Όo�ϓI���l�������Ȃ��BPC�͓d�͂̋����ƒʐM�l�b�g���[�N�����݂��Ȃ���C�ۗL���鉿�l�͂Ȃ��B
��X���d�C���i��ʐM���u���w������̂́C���ł��ǂ��ł����p�\�ȓd�̓l�b�g���[�N��ʐM�l�b�g���[�N������C���ꂪ�M���ł��郌�x���Ɉێ�����Ă���Ɗm�M���Ă��邩��ł���B����d�̓L�����A��ʐM�L�����A���l�b�g���[�N���ێ���������͍̂������d�͂�ʐM�̐ݔ���ێ�������I�Ɏg��������Ɗm�M���Ă��邩��ł���B���̂悤�ȑ��ݐM�F�i�^�M�j��^�������W�͋��b�i���j�W�iconjugate relation�j�ƌĂ��B���Ȃ킿�Q��activity�������Ĉ����activity��������activity�Ƒ��݂ɕs���ȊW�ɂ�����w���B�C���t���͂ǂ̂悤�ȎЉ�̐��ł��邩���킸�R�~���j�e�B�̈ێ��ɕs���ł���C�s��o�σV�X�e���ł͓d�͂�ʐM�C�����C�^�A�C�����Ĉ�ÂȂǂ��Љ�ʎ��{�Ƃ��đ��݂��Ă���1�j�B����������͎���I�ȕϑJ������ƌo�ϓI�Ɂu�����T�[�r�X�v��u���v���Ɓv�̊T�O�����R�̂��̂Ƃ��ă��]���E�f�[�g�����咣�ł�������̂��Ƃł������B1980�N��ȍ~�̋K���ɘa�ideregulation�j��s�ꌴ����`�Ȃǂŗ͂𑝂�����A�̎v���ł́u�����v��u���v�v�Ƃ́C�s���ʂ��ċ����������E�T�[�r�X�Ƃ̑Η��T�O�ƂȂ�C�Ƃ��ɂ͉ߋ��̈╨�܂�hanomaly�h�ƌ��Ȃ���邱�Ƃ�����B����ƋO����ɂ��Čo�ϊw�̈ꕔ����͓������ݕ⏕�icross subsidy�j�Ƃ͌o�σV�X�e������r�������ׂ����x���邢�͊T�O�Ƃ���Ă���̂����邱�Ƃ�����B���̘_�l�́u���b�v�Ƃ����T�O�̖����������ɗ��������C�Љ�ʎ��{�ɂ�����������ݕ⏕�Ƃ������x�I�ȍH�v�͎Љ�I���ʎ��{�̑����ƕs���Ȃ��̂ł��邱�Ƃ��������������Ƃ�����̂ł���2�j�B�{�e�͏W�c�I��������T�[�r�X�̐��i�������Ƃ������ɏo��d�͎Y�Ƃ𒆐S�ɕ��y230�Łz �͂��Ȃ���Ă���B�d�͎Y�Ƃł́u�d�̓V�X�e�����v�v�������I���߂���i�߂��C���݂͐V�����g�g�݂̉��ɐ��x�̉^�p�i�K�ɓ����Ă���B�u���v�v�ł͂��Ă̓d�͋����̓����ł����������������A���o���h�����Ĕ��d�Ƒ��d���������ꂽ�B���̌��ʔ��d�s��ł̋����̐��i�ƂƂ��ɁC���f���ꂽ���d����Ƒ��d����̉~���ȘA�g�ɂ��C�u�f�̂Ȃ��d�͂̋����̋ύt���������悤�Ƃ��Ă���B���̎�i�Ƃ��ē��D���x�Ɉˋ��������s��E���������s��E�e�ʎs��Ȃǂ��n�݂��ꂽ�B����d�͉�Ђ͒n��Ɛ�̃X�e�[�^�X�������ƂƂ��ɁC�u�����`���v�Ƃ������g��Ƃ�邱�ƂƂȂ����B�܂肩�Ă̓d�͎Y�Ƃɂ�����Ԏ������̎�i�ł������������ݕ⏕�̎d�g�݂͐��x�I�ɓP�p���ꂽ�B���̘_���ł́C�W�c�I��������^�̎Y�Ƃł͓������ݕ⏕���ǂ̂悤�ȋ@�\���ʂ����������邱�Ƃɂ��C�u�A���o���h�����O�v�̂����炷���x�I�������f����ޗ�����悤�Ƃ�����̂ł���B
1930�`40�N��͗��_�o�ϊw�̕���ŕ��ϔ�p�����ideclining average cost�j�Ƃ������ۂƌ��E��p�ɂ�鉿�i�Â��imarginal cost pricing�j�Ƃ����e�[�}�ɂ��Ċ����Ș_�����s��ꂽ����ł������BHotelling�i1938�j�͌��v���Ƃɂ����闿���ݒ�͌��E��p�Ɉˋ����ׂ��ł���C�s��I�ɔ�������Ԏ��͉ېłƂ����O���⏕�ɂ���ĉ������ׂ����Ƃ������C����ɑ���^�ۗ��_�����ꂽ3�j�BCoase�i1946�j�͉ېŁi���̕��@�͗l�X�����j�ɂ��Ԏ���U�͎����z����������z���������ɘc�݂������炷�Ƃ��āC���v���Ɠ����ł̗����ݒ�̍H�v�imulti-part pricing���邢��two part pricing�j�ɂ��C�Ԏ�������������ׂ����Ǝ咣�����B�R�[�X�̃A�C�f�B�A�͌Œ��̑唼���߂鋤�ʔ�ɂ��āC���v���ƃT�[�r�X�̗��p�ґ��݂Ŕ�p�̕��S�����C�Ԏ�������I�ɏ������邱�Ƃ��ł���Ƃ����咣�ł������B����ɑ���Vickrey�i1948�j�́C���ʔ�̔z�����R�X�g�E�x�[�X�ōs�����Ƃ��Ă��C���p�ҊԂł̔�p���S�͜��ӓI�Ȃ��̂ł����Ȃ��Ƃ����_���w�E�����B
�ȏ�̋c�_�ł͕��ϔ�p�ጸ�̏����̉��ł́C���E��p�����ϔ�p�ȉ��ɂȂ炴��Ȃ��̂ŁC���E��p�����������Ƃ�Ȃ�Ԏ��͕s���ł���Ƃ����_�_�𒆐S�Ƃ��Ă���B���̐Ԏ����O���i�ېł��邢�͐��{����ɂ��j�⏕�ɂ�邩����Ƃ����p�ґS�̂Ƃ��đ��݂ɕ⏕����icross subsidization�j�Ƃ��������⏕�ɂ�邩�Ƃ����g���[�h�E�I�t���_���̒��S�ɂ������B����������ȍ~�̋c�_�̏œ_�́C���g���X�g�@������v���Ƃ��ǂ����邩�Ƃ������_�Ɉڂ�C���������⏕�Ƃ����p�ꂪ�C���v���ƃT�[�r�X�̃T�[�r�X�i�ڊԂŁC����T�[�r�X�̐Ԏ��𑼂̃T�[�r�X�̍����ŕ�U����Ƃ������i���ʁiprice discrimination�j�̖��ւƈڍs���Ă������B�܂蓖���́hdeclining average cost�h�Ƃ����e�[�}�����C���i���ʂ̂������z����̃��X������Ƃ��u�������v�̍����T�[�r�X�ɐϋɓI�ɕ⏕�����ăT�[�r�X�̕��y���͂��邩�Ƃ�����肪�嗬�ƂȂ��Ă������B���̈�Ⴊ���Ă̓d�b�Y�Ɓiwireless�͑��݂���wireline�����Ȃ���������j�ŁC�d�b�̐ϋɓI�ȕ��y�̂��߂ɂ́C�s���d�b���������ɂ��Ďs�O�d�b�������炻�̐Ԏ����U����Ƃ����̂��]�܂������ۂ��Ƃ����_���ł������B���E���y231�Łz �p���i�Â��ɂ��Ă̘_���͂��Ă̂悤�ɂ͊����ł͂Ȃ��Ȃ������ˑR�Ƃ���Fishmann&Hogendorn�i2015�j�Ɍ�����悤�Ɍ��݂��p���I�ɂȂ���Ă���B�������{���I�ȕ��ϔ�p�ƌ��E��p�̘������琶����Ԏ����ɂ��Ă͋c�_����邱�Ƃ͏��Ȃ��Ȃ��Ă���B
�{�e�͖{���̎��_�ɗ����߂��ĉ��i���ʖ��Ƃ��Ă̓������ݕ⏕�ł͂Ȃ��C���ϔ�p�����ƌ��E��p�̊�{�I�ȊW�ɂ��ďœ_�Ă�B�u���v���Ɓv�Ƃ����`���I�ȗp��@�ɂƂ��ꂸ�C�W�c�I��������Ƃ����ϓ_�ɗ��ƁC�����ŋ����������̓������炢���ɂ��ĐԎ��̕�U���s�����Ƃ������͋ɂ߂Ė{���I���Ǝv���邩��ł���B���͓������ݕ⏕�Ń��B�N���[�����Ƃ������ʂ̔z�����ɂ��ẮC���ʔ�z���̈�̕��@�Ƃ��ăx�C�Y�m�������p���ăi�b�V�������ɂ�������̕s��v�_��莮�����C�i�b�V�����������Ɠ����̃����o�[�ɂ�鋦�����\�ɂ���\�������ƂȂ邱�Ƃ�_����B
�{�_���̍\���͈ȉ��̒ʂ�ł���B
�܂��W�c�I��������̓��������K���z�ŕ\���ł��邱�Ƃ������C�W�����K���z��p���ĈقȂ�^�C�v�̃T�[�r�X�ł����ĉ��I�ɕ��͉\�ł��邱�Ƃ������B��������T�[�r�X�͊m���I�ɕϓ�����Ƃ������i�������C��������ԓI�Ƀx�[�X�ƃs�[�N�̎��v�i���[�h�j�ɕ����čl���邱�Ƃ��ł���B���̂Ƃ��s�[�N���v�̓x�[�X���v��O��Ƃ��Đ��藧���Ă���B�������x�[�X���v�ɂ͌��E��p�ʼn��i�Â��imarginal cost pricing�j����C�s��I�ɐԎ�����������Ƃ�����肪����B���̐Ԏ������������ɕ�U���邩�Ƃ����_�œ������ݕ⏕�̉ʂ����ׂ������������B�����ŕ⏕�isubisidy�j�̕��@�ɂ��ăi�b�V�������̃A�C�f�B�A�����p�ł���悤�ȕs�m�������̓������ݕ⏕�̃��f�������B�Ō�ɂ��̕��͂̐����I�܈ӂƊg���ɂ��Ę_����B
�R�D�W���I��������imass collective consumption�j
�Љ�V�X�e���ŏ���҂��u�W�c�I�v�ɋ��������Ƃ������������T�[�r�X�̌ÓT��\��́C�d�͂�d�b�C�K�X�C�����C���H�C�^�A�Ȃǂł��낤�B����ł̓C���^�[�l�b�g�̕��y�ɂ���ăl�b�g��ŏW�c�ŋ��������鏤�i�����X�Ɠo�ꂵ�Ă���B�ÓT�I�ȃT�[�r�X���C���^�[�l�b�g����Ĉꕔ�̃T�[�r�X�́u�o�[�`�����v�ɋ�������邱�Ƃ��\�Ȃ��̂�����B���������̘_�l�őΏۂƂ���̂́C�T�[�r�X�̋���������ȕ����I�ݔ���K�v�Ƃ�����̂ŁC���݂��ꂽ�ݔ����T���N�E�R�X�g�ɂȂ���̂Ɍ�����B����ɂ��̂悤�Ȏ�ނ̃T�[�r�X�ł��C����҂̑��Ŏ���K���I�ȋ@���ݔ������邱�Ƃ����p����̂ɕK�{�̏����ƂȂ���̂ɒ��ڂ���B��̗��������C�d�C�͓d�C���i��@���p�ӂ��Ȃ���Ζ��ɗ����Ȃ��̂ɑ��C�S���⌀�ꂠ�邢�͕a�@�Ȃǂ͗��p�҂������֍s���Ƃ����ȊO�ɉ����@���p�ӂ���K�v�͂Ȃ��i���̂ɂ���Ă͂��̃G���A�ɋ��Z����Ƃ����R�~�b�g�̎d���͂���j�B����������Ώ���҂��T�[�r�X�������̂ɁC�R�~�b�g������x�Ɍ���I�ȍ�������Ƃ������Ƃł���B�u���v���Ɓv��public utilities�����������Ă����T�[�r�X�ɂ́C����҂������R�~�b�g�����߂���^�C�v�ƂقƂ�ǂ��ꂪ�K�v�̂Ȃ����̂��܂܂��B�O�҂͓d�́C�ʐM�C�K�X�Ȃǂɑ�\����C��҂͑����̉^�A�T�[�r�X�����Ă͂܂�B�����R�~�b�g��v���������͓̂����ɓ��퐶���ŊԒf�Ȃ����p�����Ƃ������i�������Ă���B���Ȃ킿��X�̓��퐶���́C�d�͂�ʐM�̃l�b�g���[�N�Ȃ��ɂ͐��藧���Ȃ��B�ȉ��ŏW�c�I��������Ƃ��Ă�����O���ɒu���ĕ��͂�i�߂邪�C���̑��̃^�C�v�Ƃ̊֘A�͌�ɐG��邱�Ƃɂ������B
�y232�Łz���ēd�͂�ʐM�Ȃǂ̃l�b�g���[�N�͖c��Ȑ��̗��p�҂������Ă���B�]���ė��p�҂��ǂꂾ���d�͐ݔ���@�킠�邢�͒ʐM�@���ۗL���Ă��邩�C����ɂ��ۗ̕L�ʂɉ����ĉ����Ԃ���𗘗p���邩�i�P���C�P���C�P�N�ȂǂŁj�͊m���I�Ȍ��ۂƂȂ�B�����Ă��̂悤�ȑ�W�c�͑吔�̖@���i���S�Ɍ��藝�j�ɂ���ė��p�̑ԗl�𐳋K���z�ŋL�q���邱�Ƃ��ł���B
���Ƃ��ēd�͎Y�Ƃɂ��Č���ƁC���p�҂̐��͖c�傾����C���p�҂ۗ̕L����kW���͑吔�̖@���ɂ���Đ��K���z����ł��낤�B���C�Q��ނ̎��v�҂ɂ��āC���K���z����kW����`�����̂����̐} − �P�ł���i����͂����܂ŃC���[�W�}�ł����Č����̂��̂ł͂Ȃ��j�B
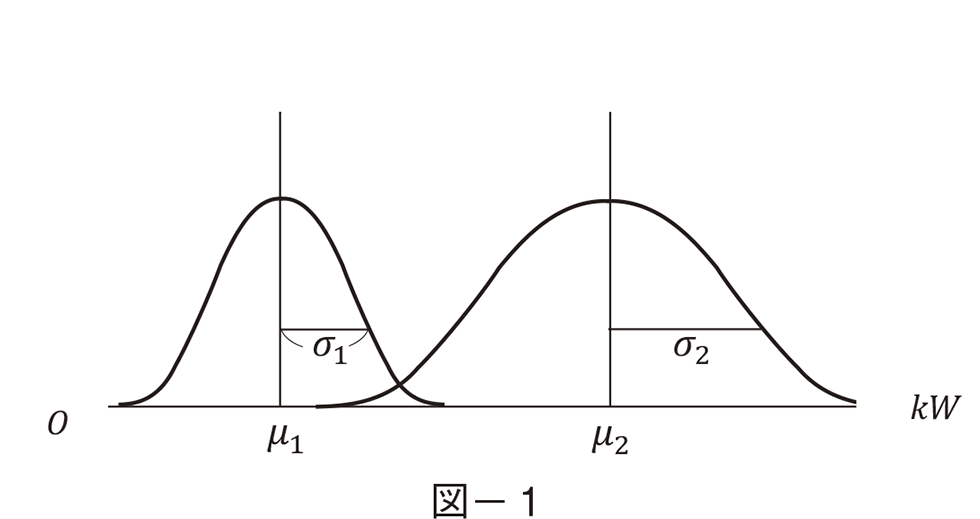
�} − �P�ō����̕��z�͈�ʂ̉ƒ�̗��p�� − − �ƌv�ƌĂԂ��Ƃɂ��� − − �ۗ̕L���Ă���d�C�@��̕��z��kW�ŕ\�������̂ł���B�E���̕��z�͎Y�Ɨp�ɕۗL����Ă���ݔ��̕��z�Ŋ�Ƃۗ̕L���z�Ƃ���B�i��1,���P�j�͉ƌv�ۗ̕L����ݔ��̕��ϒl�ƕW�����C�i��2,��2�j�͊�Ƃ̂���ł���B
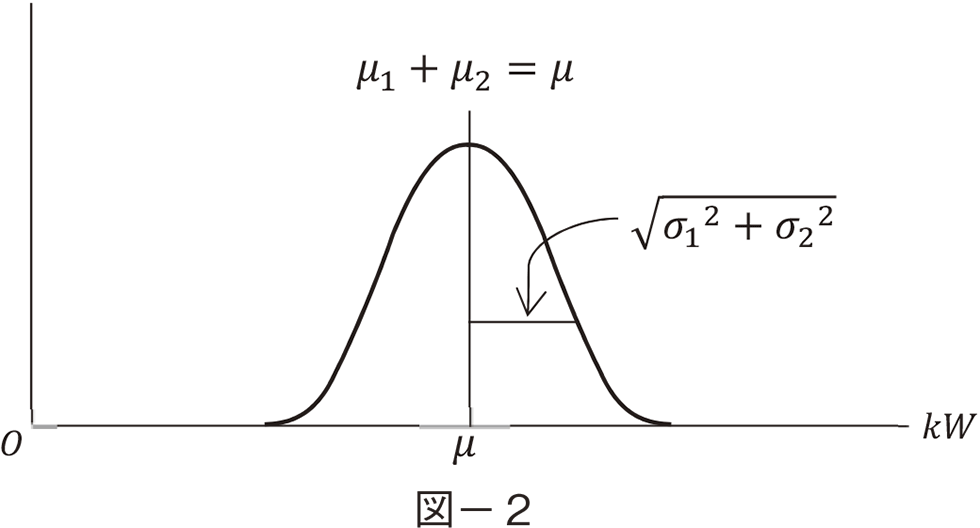
�d�͉�Ђ͂��̂悤�Ȏ��v����kW���z�ɑ��āC�ߕs���Ȃ�kW����������i���Ă͋����`���ł��������C���݂͓d�̓V�X�e�����v�ɂ���ĕύX���ꂽ�B���̓_�ɂ��Ă͌��_�̕����Ř_����j�B���������ēd�͉�Ђ͋����V�X�e���𗼎҂̍��v�����悤�ɐv���Ȃ���Ȃ�Ȃ��B�܂�d�͉�Ђ̒��ʂ���kW���͎��̐��K���z�Ŏ������B
���̐} − �R�́C�C�ӂ̓d�͉�Ђ̂���G���A�̂P�N�Ԃ̓d�͎g�p�_��ikW�j�̕p�x���z����̓I�ɕ`�������̂ł���B�����ł́C�N�ԍŏ��̌_��ʂ���N�ԍő�̌_��ʂ܂ł���蕝��kW �ŋ��C�c���ɂ͂��̋�Ԃɂ�����_��ʂ��S�̂̉����ɓ����邩���������p�x�i�x�y233�Łz ���j��������Ă���B����Ɉ��̋�Ԃ̕�������Ɏ��Ƃ��ɂ́C�p�x���z��A���^�̊m�����x��f�ix�j�Ŏ������Ƃ��ł���B�A��û�͂��̊��Ғl�ł���B
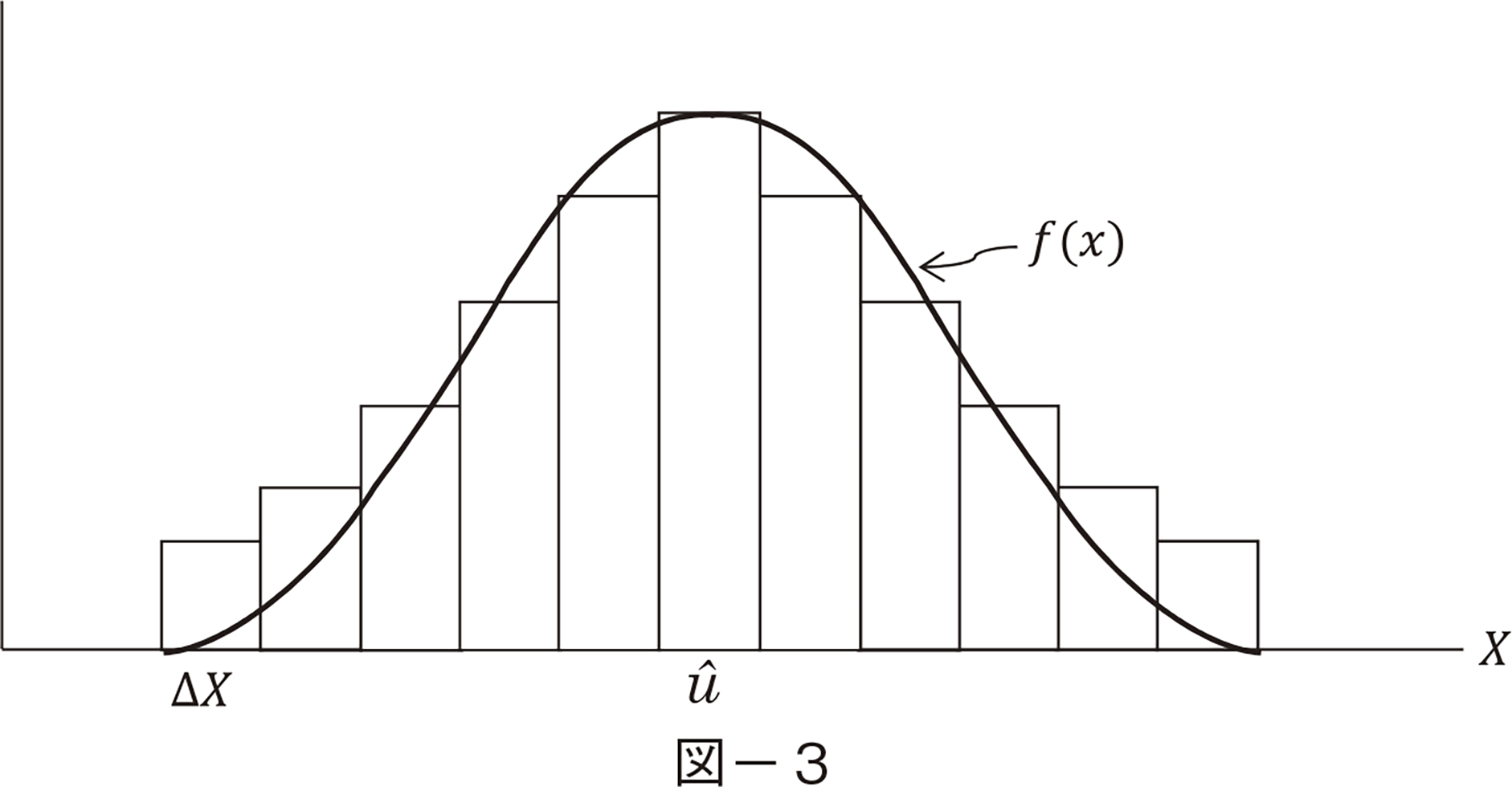
����ȓd�̓l�b�g���[�N�ɉ������Ă��闘�p�҂����E�ǂꂾ���d�͂�K�v�Ƃ��邩�̓����_���ɔ�������m�����ۂł���B�܂艡���̓d�͌_���X�͊m���ϐ��ŁCX�̔����ω�dx���m�����x�ƌĂԁB���m�����x����fX�Ƃ���BX��dx���������ω�����Ƃ��ɂ͗ݐϕ��z��FX����`�ł���B�}−�R�̊m�����x���͂���ʂ̃P�[�X��`�������̂����C������K�����̎葱���ɂ���ċK�����K���z�ɕϊ��ł���B
�}−�S�͂Ƃ���W�������ꂽ���K���z�ɂ��ĕ��ϒl��i�ƕW������i��Ꭶ�I�ɕ`�������̂ł���B�܂�ʂ̐��K���z�͋K�����̎葱�����s�����ׂẮi��i, ��i�j�͕��ϒl�O�C�W�����P�̕W�����z�ɏ�����������B���Ȃ킿�C�m���ϐ�x�̕��σʁC�W�����Ђɂ���Z�Ƃ����ϐ�������B

�����Z���m���ϐ���

������Z�͎��̂悤�Ȋm�����x����^����B

 �y234�Łz
�y234�Łz
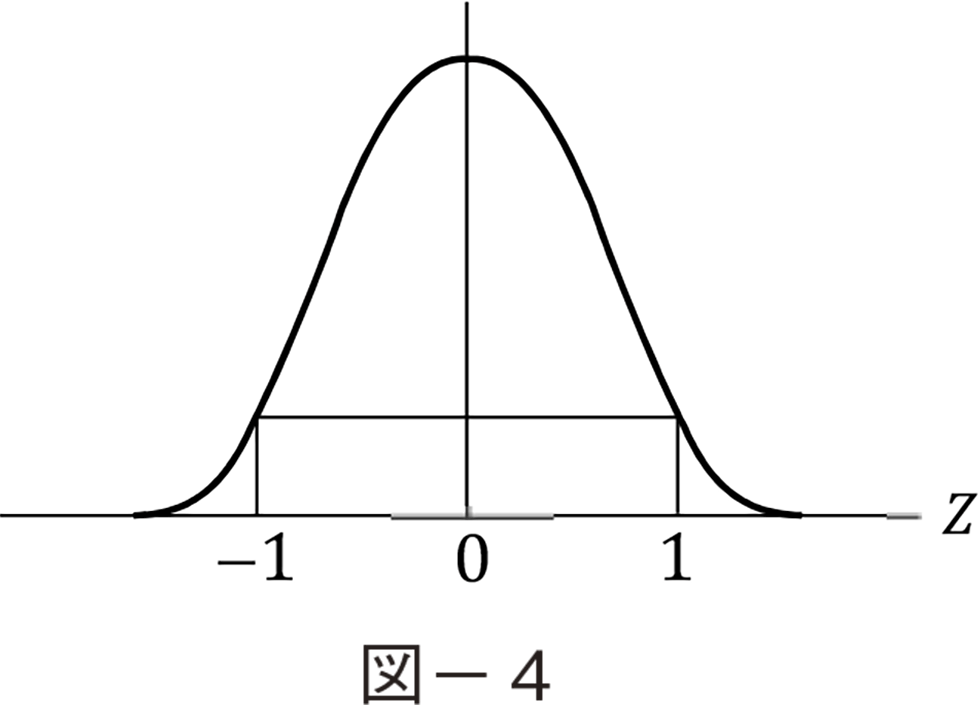
���̕W�����z���g���C�ϐ�Z�̒l�ɂ���ĉ��}�̂悤�Ɏΐ������őS�̂̉����ɂ����邩���������Ƃ��ł���B���Ғl�O�̍��E�̖ʐς͑Ώ̂�50�����ɂȂ��Ă���B�Ⴆ��Z=0.5�̂Ƃ��ΐ������͑S�̖̂�70���������Ă���B
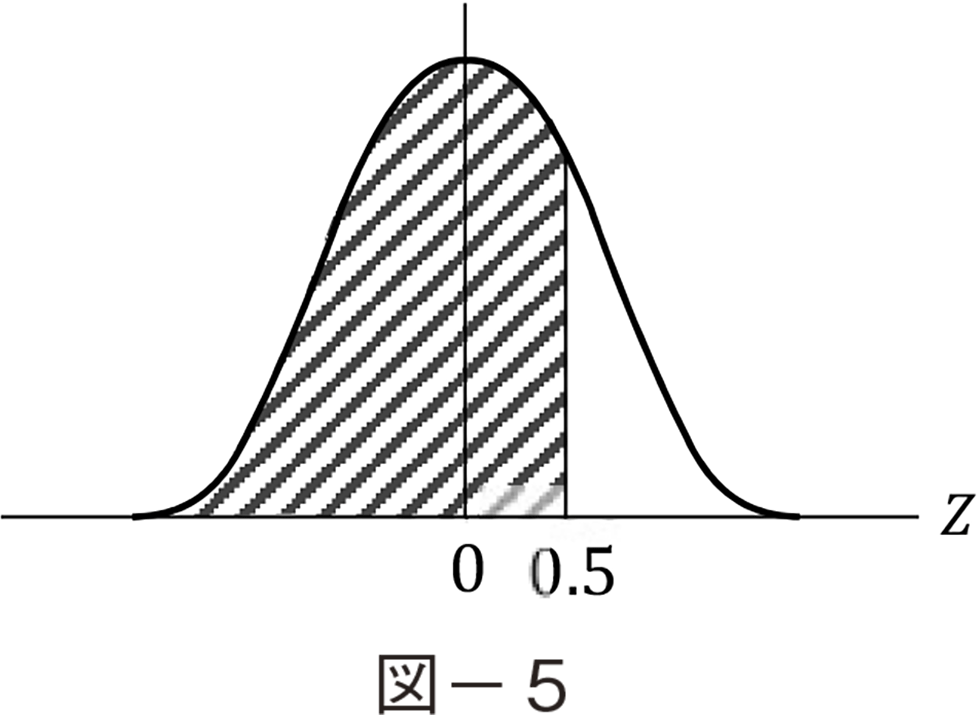
�d�̓T�[�r�X���ɂƂ�ƁC���b�W����̓I�ɃC���[�W�ł���B�d�͎��v�͎��ԑтɂ���đ傫���ϓ�����B��ʓI�ɂ͎��v�����ԓI�Ƀx�[�X�E�~�h���E�s�[�N�Ƃɕ����čl����̂����ʂł���B�܂�x�[�X�Ƃ͂قƂ�ǂ̗��p�҂��펞�d�C�̃X�C�b�`���u�I���v�ɂ��Ă����ԂŁC�s�[�N�͓��ɓd�͂��ʂɕK�v�Ƃ��鎖�Ǝ҂�����̎��ԑтɔ�����������v�ł���B�����ł��̎��v�̃p�^�[����}−�U��p���Đ}�����邱�Ƃ��ł���B�Ⴆ�x�[�X�͑S���v�҂�50�������p����Ƃ����Ƃ����炻��͐}−�U�̃{�J�V�̕����̖ʐςŎ����邵�C�s�[�N�Ƃ�70�������p����Ƃ����Ƃ�����}�̎ΐ�����������������Ă���B
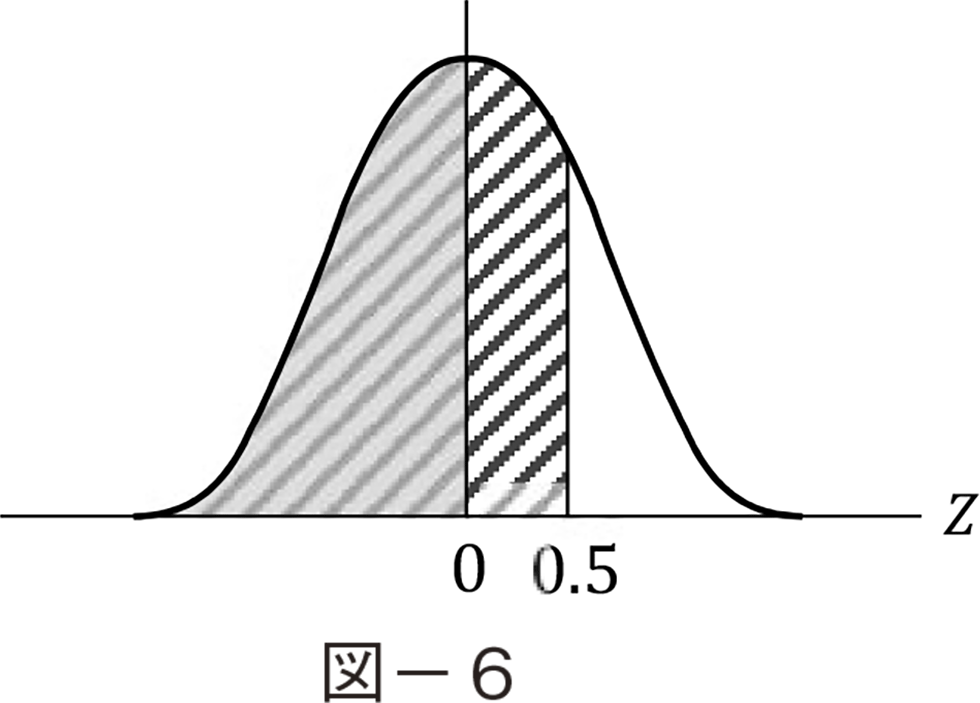
�d�͋������͂��̂悤�ɕϓ�������v�ɑ��Ēx�Ȃ���������K�v������B�������̃��X�y235�Łz �|���X���傫�������ƁC���g���ɗ��ꂪ�����ĂƂ��ɂ͓d�̓V�X�e�����_�E�����u��d�v����Ƃ����\�������邩��ł���B���Ȃ킿�d�͎��v�Ƌ����Ƃɂ́C���}�̂悤�ȃ}�b�`���O�̃V�X�e������ΓI�ɕs���Ȃ̂ł���i����͕����I�ȗv���ł����ēƍَ҂ł��ς��邱�Ƃ͂ł��Ȃ��j�B
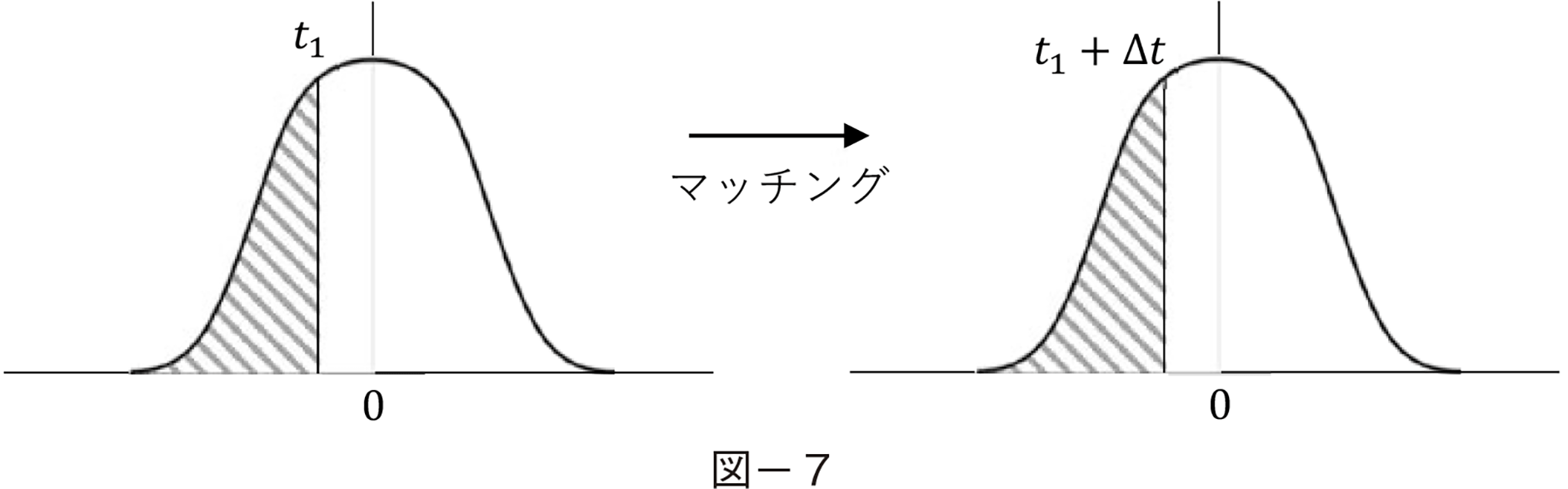
�}−�V�ł�t1�Ƃ������_�̎��v���ΐ����Ŏ������Ƃ���C�d�͉�Ђ̓�t�Ƃ����ʑ��̂���͐����邪���₩�i�܂���g�����傫���ϓ����Ȃ��j�ɂ��̎��v�Ƀ}�b�`�����d���𑗂�Ȃ���Ȃ�Ȃ��B
�ȏ�̎��Ⴉ�狤�b�W�Ƃ����Ӗ��͖��炩�ł��낤�B�d�͂Ɍ��炸�C�d�C�ʐM�ł��K�X���Ƃł����̂悤�ȑ��݈ˑ������݂���B���̊W�͐}�̉E���̃V�X�e���������̃V�X�e���Ǝʑ����邢�͒P�˂̊W�ɂ���Ƃ������������C���w�I�ȕ��͂��W�J�ł���4�j�B
���b�W�͌���������C�T�[�r�X���p�҂��������̃V�X�e���E�l�b�g���[�N�Ɂhlock-in�h����Ă����Ԃ��邢�͔��g���X�g�@�I�Ɍ����Η��p�҂������҂Ɂhcapture�h����Ă����ԂƂ�������B���������ė��p�҂����ɑ�֓I�ȋ����҂��i�����o������Ƃ��ɂ́C���b�W�͎キ�Ȃ�B
���̂悤�ȈӖ��œd�͍͂ł�������ł��낤���C��r�\�ȎY�Ƃ�������Ǝ��̂悤�ɂȂ�B
�s�s�K�X�E�����͗��p�҂��T�[�r�X�𗘗p�ł���ꏊ�����肳��Ă��ĉ����҂����{�����������ł���Ƃ����_�œd�͂ɋ߂��ƌ�����B
����d�b�Y�Ƃ́C���Ă͓d�͎Y�ƂƔ��ɋߎ�������Ԃɂ������B���������C�����X�Z�p�i�ړ��̒ʐM�j�̓o��ɂ���ă��C�����C���ɌŒ肳�ꂽ�d�b�͎���̍����������B�܂������܂ł��Ȃ��C���^�[�l�b�g�Z�p�ɂ���ēd�b��ITC�Y�Ƃ̈ꕔ�ɂȂ�C�����I�Y�Ƃ̐��i�����܂��Ă���B
�����C�S���E�q��E�������H�Ȃǂ͑�֓I��i�����݂���̂ŗ��p�҂̎��R�x�͍����B�������l�b�g���[�N�^�T�[�r�X�����Ƃ����_����̓s�[�N�ƃI�t�E�s�[�N�̑��݂�����C�����ł͗������x�̍H�v���\�ł���5�j�B
�W�c�I��������Ƃ͊m���I�ɕϓ�������v�ɑ��Ēx�Ȃ��������}�b�`���O�����邱�Ƃł���B���̂Ƃ��s�[�N���̎��v�̓x�[�X�̎��v����ɏ[�������邱�Ƃ�O��Ƃ��Đ��藧���Ă���B�����ł͕��͂�P���ɂ��邽�߂Ƀ~�h���ƃs�[�N�̎��v�����v�������̂��s�[�N���v�ƌĂԂ��Ƃɂ���B
�������Ǝ҂͂��̂Q�̎��v�𗼗�������悤�Ȏ��{�ݔ���v���˂Ȃ�Ȃ��B�R�X�g�Ƃ����ϓ_����͍ő�̎��v������悤�ȖڕW���Ɠx���߂Ă����ŃR�X�g�̍ŏ������v�悵�Ȃ���Ȃ�Ȃ��B�}−�S�Ŏ������W�����z�ɂ��Č���CZ�Őϕ�����ƍő�̖ʐς͂P�ƂȂ邪�C�����̎��v�̔������P�ƂȂ邱�Ƃ܂�d�͗��p�҂��ׂĂ������ɃX�C�b�`���I���ɂ���Ƃ������Ƃ͂��肦�Ȃ��B�K���u�I�t�v�̏�Ԃɂ��Ă��闘�p�҂�����͂�������ł���B�����ŋ������Ǝ҂͊m���I�Ɏ��v�K�͂𐄒肵�C�R�X�g���ŏ��ƂȂ�悤�Ȑv���s�����낤�B���Ȃ킿�C���{�ݔ��K�͂��^�����鎞�C�R�X�g���ŏ��ƂȂ鐶�Y������ڕW���Ɠx�ƒ�߂�B����͒Z���̕��ϔ�p�iAC�j�ƌ��E��p�iMC�j����v����_�ɑ��Ȃ�Ȃ��B
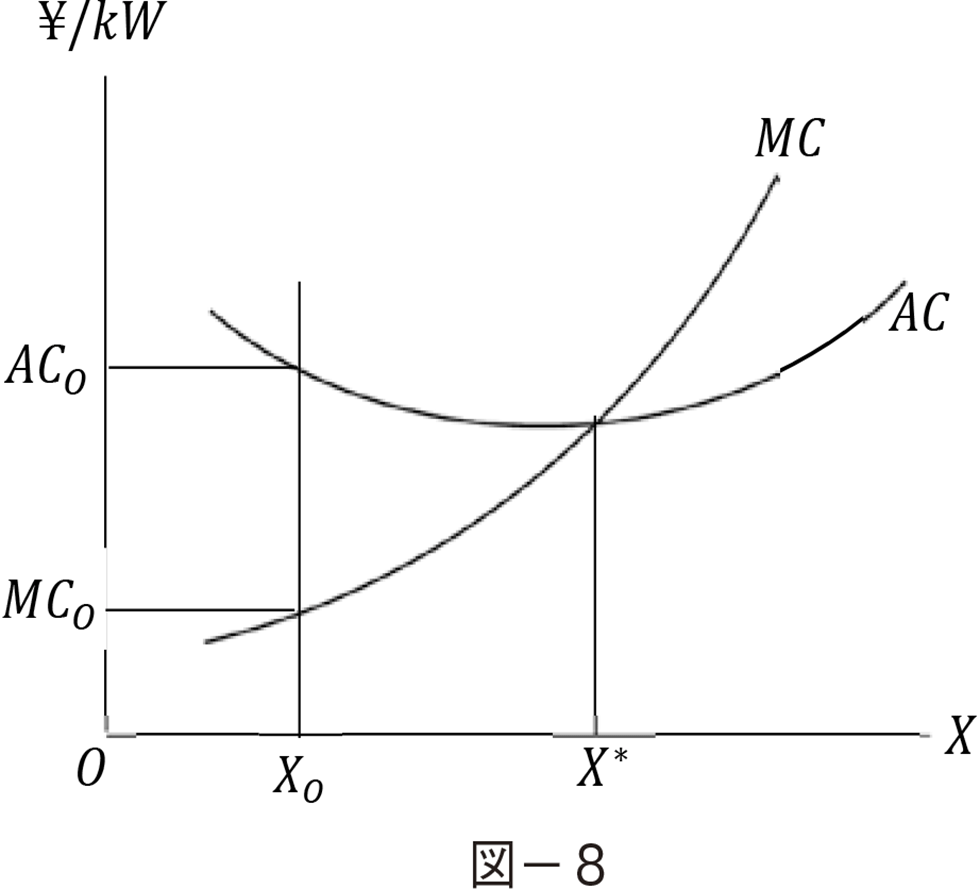
���̐}−�W�ɂ����ăR�X�g���ŏ��ƂȂ�̂́CAC��MC�Ƃ���v����X*�Ƃ��������ł���B�����Ă��ꂪ�^����ꂽ�ݔ��ŒB�����ׂ��ڕW���Ɠx�ƂȂ�B
�}−�W�Ŕ��d�ʂ�XO�̂悤�ɏ������Ƃ��CAC��ACO�CMC��MCO�ł���B���������������ϔ�pACO�ʼn��i������ΒP���͍������v���̓d�͂𗘗p���悤�Ƃ���C���Z���e�B�u�͒��������Ȃ��邾�낤�B�t�ɐݔ��������MCO�ŗ���������C���v�͊��N�����B���������̂Ƃ��ɂ́CACO��MCO������CACO−MCO�����̐Ԏ�����������B�܂苟���҂̓W�����}�ɒ��ʂ���B�����I�Ȏs��ł͂��̃W�����}�̑��݂����Ɖ�������ɂ���̂ł���B��������T�[�r�X�Ƃ��ēd�͂���������Ƃ������ꂩ�炷��ƁC���ł���d�͂͂ł���������ōL�����y�����邱�Ƃ��ڕW�ƂȂ�B���Ȃ킿�s��I�ɔ�������Ԏ��𐭍��I�ɉ�������Ƃ����A�v���[�`���K�v�ł���B
�����Ŕ�������Ԏ��Ə���җ]��̊W��}−�X�ɂ���ĕ��͂���B���v���͗��ۉ��i��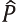 �Ƃ��Ē����ŋߎ�����B��Ƃ͐Ԏ��������Ȃ����߂ɕ��ϔ�pAC�ŗ���������Ƃ���Ή��i��PA�ł���B���̂Ƃ������������җ]��̑傫���͐}�̎ΐ�������F�ł���B������������E��pMC�ɂ���Č��߂�Ƃ���Η�����PM�C���Y�ʂ�XM�ƂȂ����җ]��͂R�p�`
�Ƃ��Ē����ŋߎ�����B��Ƃ͐Ԏ��������Ȃ����߂ɕ��ϔ�pAC�ŗ���������Ƃ���Ή��i��PA�ł���B���̂Ƃ������������җ]��̑傫���͐}�̎ΐ�������F�ł���B������������E��pMC�ɂ���Č��߂�Ƃ���Η�����PM�C���Y�ʂ�XM�ƂȂ����җ]��͂R�p�`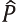 ��PM�ł���i���̖ʐς����G�Ƃ���j�B
��PM�ł���i���̖ʐς����G�Ƃ���j�B
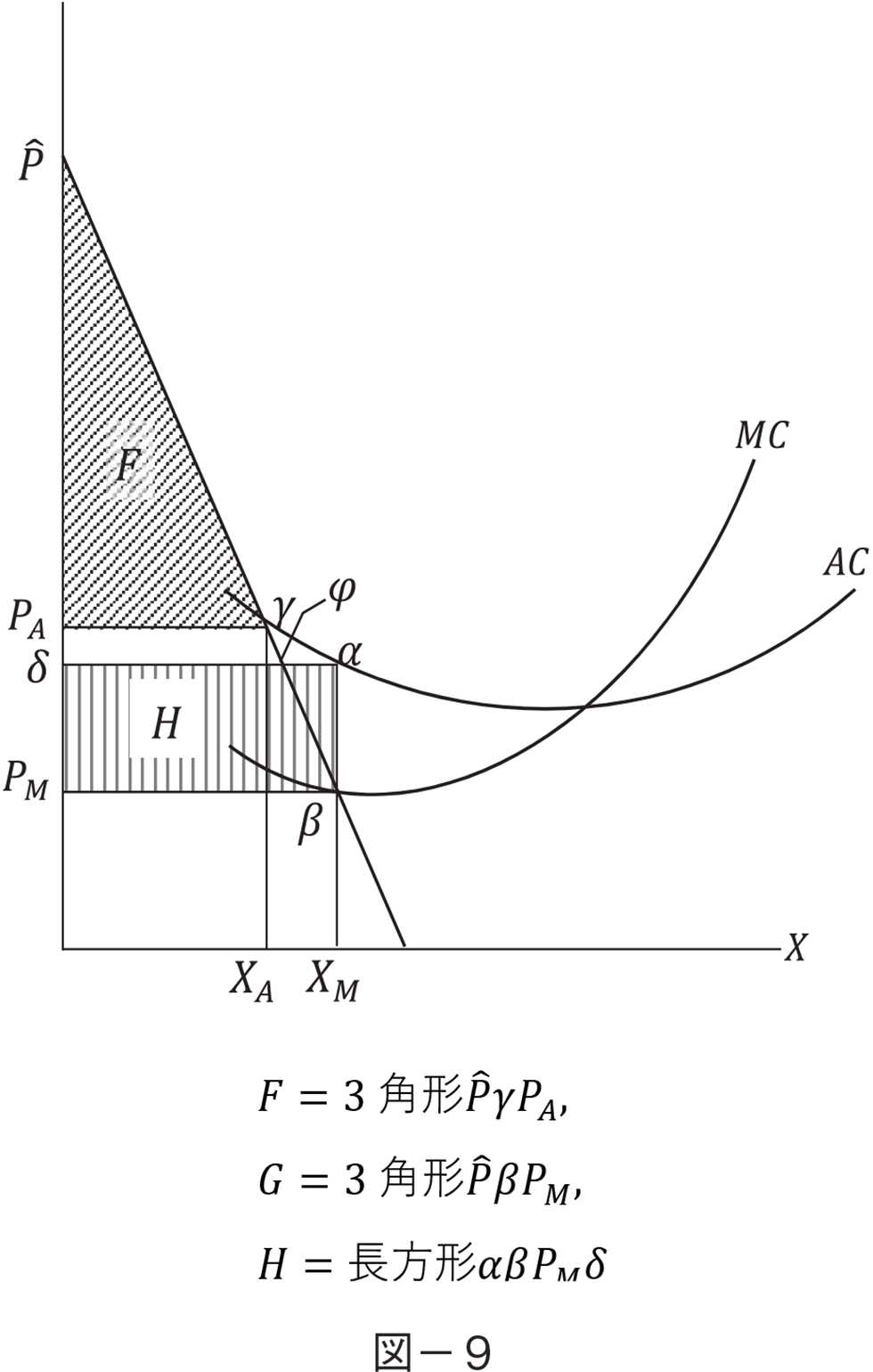
MC�Ǝ��v�Ȑ��̌�_XM��AC���ቺ�������Ă���̂�XA�����傫���B�����ĐԎ��zH������PM�ł���B�}−10�łR�p�`��������Dead Weight Loss�i�Љ�I�������j�ł���B���̑傫���ɂ��Č���ƁC���i�e�͐��͔��ɏ���������XA����XM�ւ̑����������́CXA�܂ł̐��Y�ʂƔ�ׂ�Ɩ����ł���I�[�_�[�ł����Ȃ��B�܂�R�p�`�̖ʐς͖����ł���B��`PA�����̖ʐς�PA��PA PM�ɔ�ׂĔ����ł���̂ł����Ԏ��zH�ɉ����Ă��ω��͖����ł���B���̌��ʁC���E��p���iPM�����藧�Ă��̂Ƃ��̏���җ]��̑����͑�`PA����PM�ƂȂ�B�܂�Ԏ��zH�͌��E��p���iPM�̂����炷����җ]��̑����ƌ����Ƃ��ł���B
���_�Ƃ��ĕ��ϔ�p���iPA�ɂ�����җ]��F�ƁC���E��p���iPM�ɂ�����җ]��̑���H�Ƃ̘a�����iPM�ɂ��g�[�^���ȏ���җ]��G��
G = F + H
�ƂȂ�B
�y238�Łz�T−�Q�@�Ԏ��̋���������o�[�ɂ���U
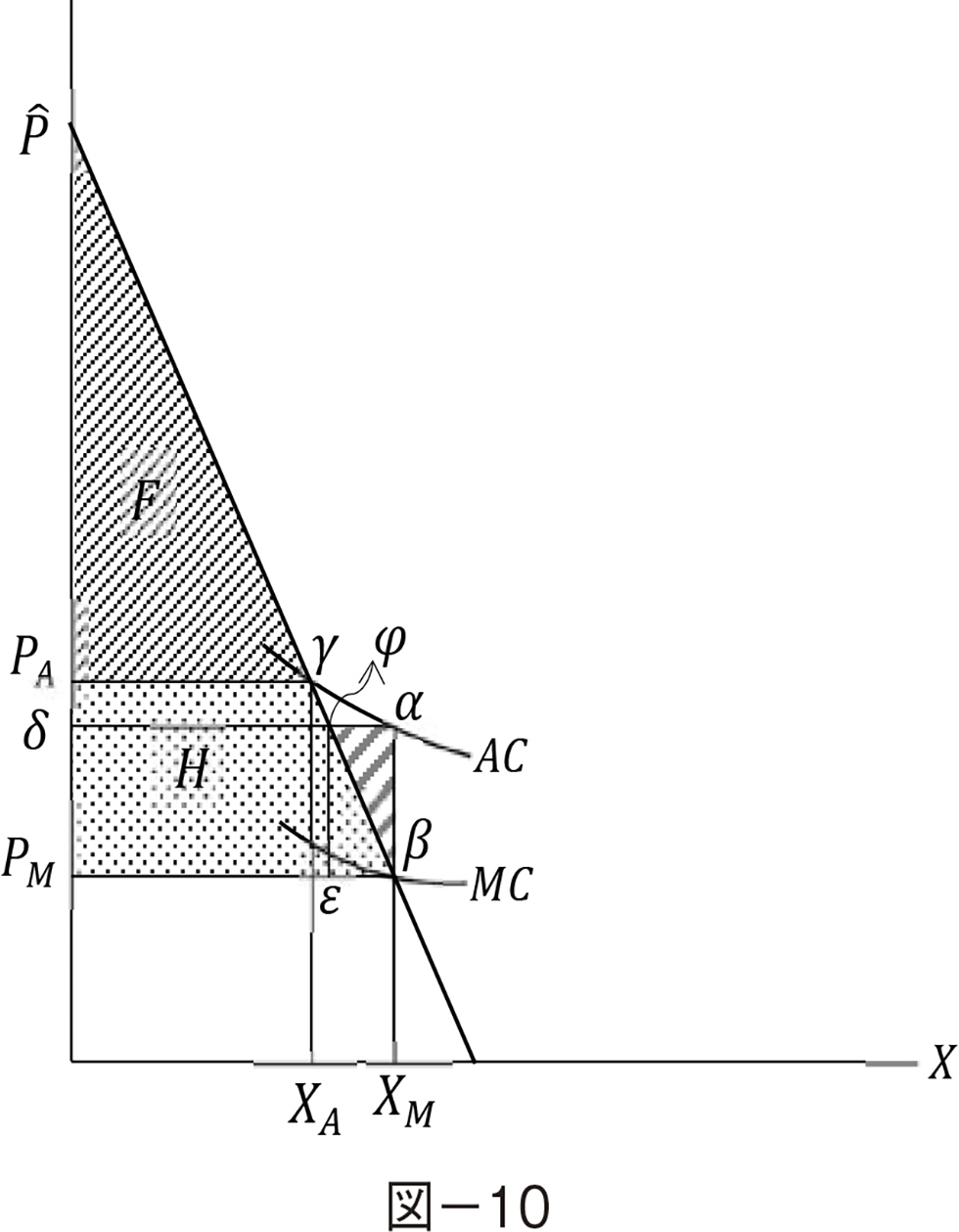
�����œ������ݕ⏕�Ƃ����Ƃ��u�����v�Ƃ͉�����}−10�̃��f���ōl����B�}−10�ŕ��ϔ�p���i�������炷����җ]��͂R�p�`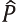 ��PA�ł���B���̂Ƃ��̗��ۉ��i
��PA�ł���B���̂Ƃ��̗��ۉ��i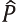 ��AC�ɂ���Ď��̂悤�ɕ\�����B
��AC�ɂ���Ď��̂悤�ɕ\�����B
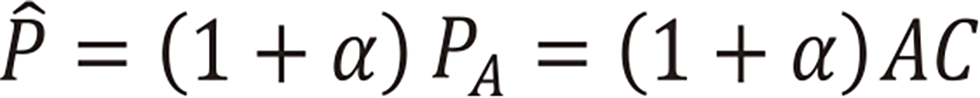
���͗��ۉ��i��AC���ǂꂾ�������Ă��邩���������̂ŗ��ۗ��ƌĂڂ��B
����ƂR�p�`�̖ʐ�F��
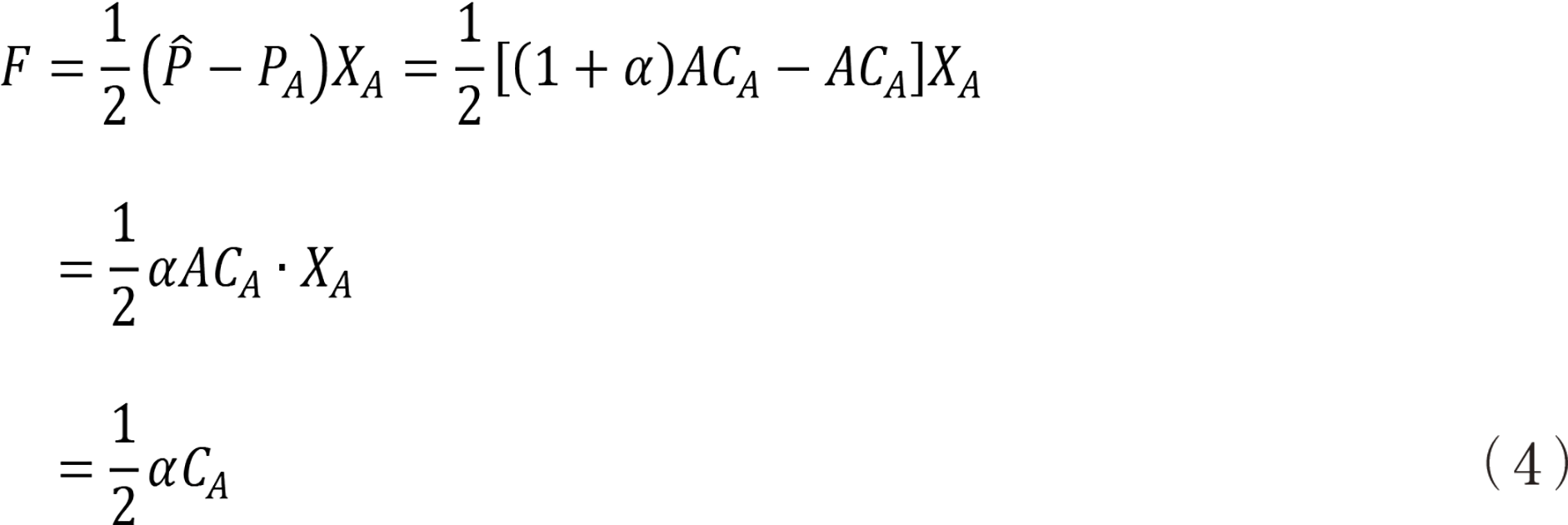
�ƂȂ�BCA�͐��Y�ʂ�XA�̂Ƃ��̑���p�ł���B����Ԏ��z�͗]��zPA����PM�ƌ����Ƃ��ł���̂ł��̑傫��H��
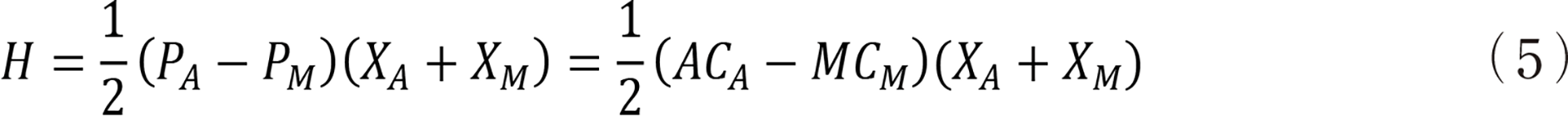
F�͉��i��PA�̂Ƃ��ۏႳ���]�肾����C����ɂ��Ԏ��zH����������CH���x������G��Ƃ����C���Z���e�B���������B
���ϔ�p���������Ǝ��̂��Ƃ�������B
 �y239�Łz
�y239�Łz
�����ό`�����
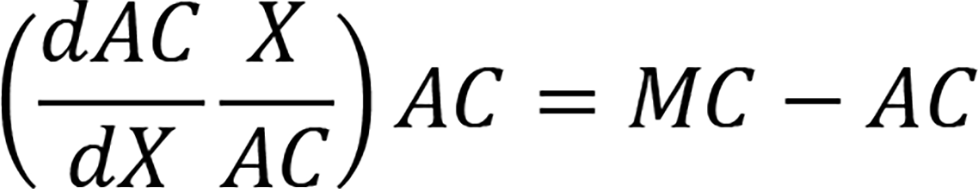
���ϔ�p�̐��Y�ʂɊւ���e�͐����ƂƌĂԁB�Ɓ�0�Ƃ���Ƃ����ł�AC�͌������Ă���̂�

�����p���āi�S�j������������
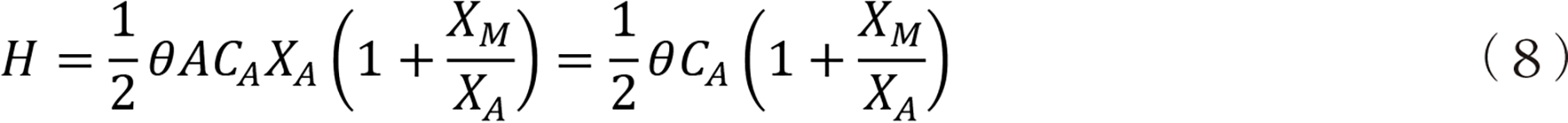
�Ƃ͓����Ɏ��̂悤�ɂ��������Ƃ��ł���B
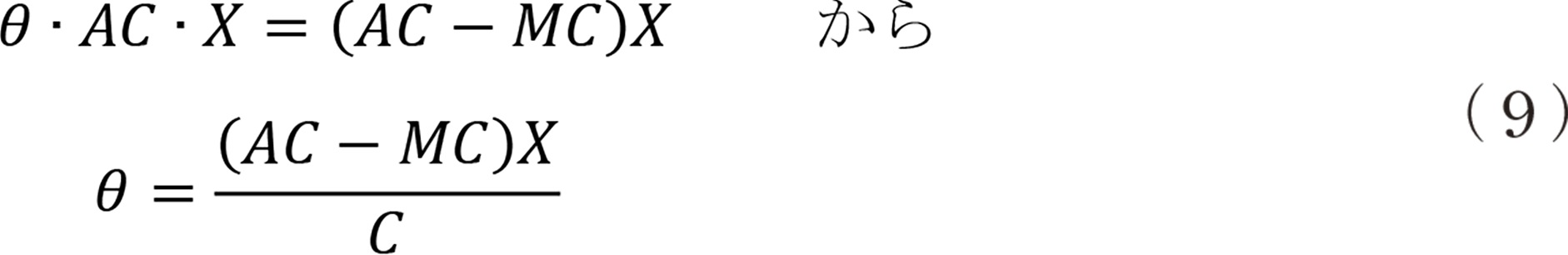
�܂�Ƃ͑���p�ɑ���Ԏ��z�̔䗦�ł���u�Ԏ����v�ƌĂԂ��Ƃ��ł���B
�i�S�j�̗]��́i�W�j�̐Ԏ�������Ȃ���Ȃ�Ȃ��̂Łi�S�j�Ɓi�W�j�Ƃ̊Ԃɂ͎��̊W�����藧���Ȃ���Ȃ�Ȃ��B

�]����

��������̃����o�[���Ԏ������������ĕ��S����ӗ~�����邽�߂ɂ́C���ۉ��iP�����ϔ�p�������Ƃ�u���v���\���傫���Ȃ���Ȃ�Ȃ��B
�i10�j�̉E�ӂ�XM�͏��XA�����傾����

���Ȃ킿�Ƃɂ���

�Ƃ͐�q���������Ԏ����ł���B�Ԏ�����F�̂�Ƃ藦���������̂Q���̂P�ȉ��łȂ���Ȃ�Ȃ��B���ꂪ�C�W�c�̃����o�[���������ݕ⏕������ӗ~�������߂̕K�v�����ł���B
���̃��f���ł�F�Ƃ����]��͋�������̃����o�[�ł���ƌv�Ɗ�Ƃ����S����B�ł͂��̗��҂��ǂ̂悤�ɕ��S����̂������I���ɂ��ẮC���߂Ō�������B
�y240�Łz�����o�ςƂ��čl����Ό��E��pMC�Ő��Y���邱�Ƃɂ͂Q�̐��������ׂ����R������B���ɑ��]��͉��i��PM�Ƃ����F����H�����傫���Ȃ�C���������ő�ƂȂ�B���ɂ͓d�͂�ʐM�̂悤�ȍ��͂��ׂĂ̐��Y���̑f�ނ��Ȃ����̂����炻�̉��i�͐��Y���̉��i�Ɏ��X�ɓ]�Łipass through�j�����B�d�́C�ʐM�Ȃǂ̃R�X�g�����E��p�Ɋ�Â��Ă�����ꂾ�������o�ϓI�Ɍ����I�ȃR�X�g�������ł���B
���߂͊O���⏕�ɔ��������o�ϓI���������C�����I������s�����p�҂��������Ď����I�ɐԎ��̕�U���s���C�ő�̗]��G��B�������̃v���Z�X���x�C�Y�m���̍H�v�ƃi�b�V�������Ƃɂ���Ė������悤�Ƃ�����̂ł���B
�W�c�I��������T�[�r�X�ɂ��ēd�͎��v�ғ��m�����͂��Č��E��p���i�������ł��邩�ۂ��Q�[���Ƃ��čl���Ă݂悤�B�d�͂��ɂƂ�Ύ��v�҂͑�ʂ���Ί�ƂƉƌv�Ƃɓł���B�O�҂͓d�͂����Ђ̐��i�Y����ׂ̃C���v�b�g�Ƃ��ė��p����B�܂�d�͂͂��̑��̑f�ނƓ��������ԍ��ƌ����B����ƌv�͓d�͂����ێ����邽�߂̍ŏI������Ƃ��čw������B�܂藼�҂͌ڋq�Ƃ��Č����ȈႢ������B�����ŐԎ����S����Ƃ������ƂƉƌv�͋������Č݂��ɕ��S��[���I�ɃV�F�A�ł��邩�ۂ����C�Q�[���_�I�ɕ��͂���B���̂Ƃ����p�ł��鋦���Q�[���̈�Ƃ��ăi�b�V�����Q�[�����̗p����B�����i�b�V����������������Ȃ�C�v���C���[�ł����ƂƉƌv�͋������郁���b�g�������Ƃ��ؖ��ł���B�܂苦�����ĐԎ��z�S����C���Z���e�B�u�����̂ŁC�������ݕ⏕�����藧�\��������������B
�i�b�V���̋��̓Q�[���Ƃ��Ēm����Q�l���Q�[���ł́C���̌��ʓ�����B��̋ύt���������I�ɋ��߂邱�Ƃ��ł���B�i�b�V������̂ɕK�v�Ȍ����n���ȒP�ɂ܂Ƃ߂�Ǝ��̂悤�ɂȂ�6�j�B
�@�����̃p���[�g�œK��
�Ԏ����ƌv�Ɗ�Ƃ����S����Ƃ����Ƃ��C�ǂ���̕��S������̕��S��������C�����̕��S���K������Ƃ������������Ȃ���Ȃ�Ȃ��B�܂藼�҂ɂƂ��Ă��͂���P���s�\�ȕ��S�̂���������߂���B
�A���ɂ����铖���҂̑Ώ̐�
���ɂ���ĂQ�����҂̓�����p�݂͌��ɓ������B�܂����������������ł���悤�ȗ͂������Ƃ͂Ȃ��B
�B�����̐��ꎟ�ϊ�����̓Ɨ���
�������p�����[�^�ɂ���Ĉꎟ�ϊ����C�ʂ̌����Ƀg�����X�t�H�[�������Ƃ��Ă��C���͕ς��Ȃ��B�܂�Q�����҂̌��p�̎ړx�͕ϊ��ɂ���ĉe������Ȃ��B
�y241�Łz�C�����̖��W�ȑI��������̓Ɨ���
�����Ƃ��ē�������̂́C�����グ���Ă���������܂ނ��傫�Ȍ������l�����Ƃ��Ă��C���̑傫�Ȍ����ɂ���ĉe�����Ȃ��B�܂萭�{�̉���Ȃǂ��傫�ȃX�P�[���Ō����Ȃ����Ƃ��Ă��C�i�b�V�����͓Ɨ��ɂ��̒��Ő������Ă���B
���Q�[���͂���ɂ͂܂��u�����\�W���v�Ɓu���̕s��v�_�v���`���˂Ȃ�Ȃ��B�v���C���[�͊�ƂƉƌv�ł���C��Ƃ̌����邱�Ƃ̌��p��uA�C�ƌv�̂����uB�Ƃ��悤�B���ɂ���ċ����ɐ�������Ƃ������\�W��U��

���j�I�Ɍ��v���Ƃ̒m�b�Ƃ��ēd�͋����҂��̗p���Ă����̂́C�c��Ȑ��̗��p�҂�����Ƃ��́C�Ԏ�����H����{���Ƃ��ČX�̗��p�҂ɐ������ĂP�l������̒lj��x�o���������Ă����v�Ȑ��̌`��͕ω����Ȃ��悤�ɂł��邾�낤�Ƃ����z��ł���B�����[�U����Ni�Ƃ��C�P���[�U������̕��S�z��ei�Ƃ����

���̌��v���ƌ^�̕��S�^�C�v��O��Ƃ���Ύ��v���̌`��͕s�ςƉ��肷��B
uA��uB�����͂��Ď������悤�Ƃ��Ă���̂͏���җ]��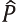 ��PM = G�ł���B
��PM = G�ł���B
����Ǝ��̐��K�v�ł���B

����������������s�����ƂȂ�Ƃ����i��PA�ɂȂ�̂ŁC���v�ґ��ɋA�����闘���͂�F����B���҂̎�蕪��dA�CdB�Ƃ���C
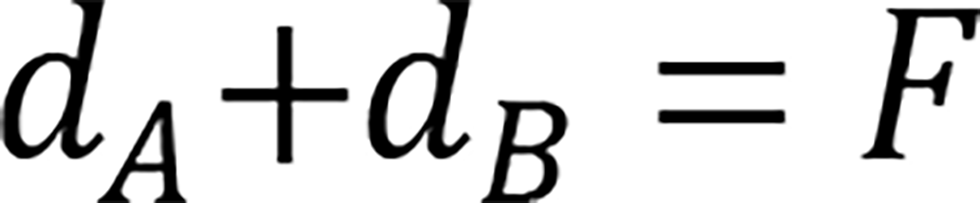
�i�b�V�������͈ȏ�̂悤�ȏ����̉��Ŏ��̃i�b�V����N

���ő剻���邱�Ƃɂ���ċ��߂邱�Ƃ��ł���B
dA��dB�Ƃ��ҊԂłǂ̂悤�ɔz����������I�������ɍl����B����җ]��G�͎��v�҂��ۗL����@����u�I���v�̏�Ԃɂ��đ��d���ԂƐڑ������Ƃ��ɂ̂ݔ������闘���ł���B���d���͑S���p�҂̋��ʐݔ�������I���̏�Ԃő��d�������v�҂������ŗ��p����̂��K�{�̏����ł���B���������ċ��ʔ�ł��鑗�d���̃R�X�g����ƂƉƌv�łǂ̂悤�ɔz������Δ[���I���Ƃ������������Ȃ���Ȃ�Ȃ��B������E��p�Ŕ��d���ď���җ]����ő�ɂ���Ƃ��������́C���d���̉ғ������ő�ɂ���Ƃ������Ƃ��Ӗ�����B�܂著�d���������Ƃ����G���Ă���Ƃ��̊�ƂƉƌv�̍����I�z���䗦�����߂�C�����n�߂�ɓ������ē������y242�Łz �ƂƉƌv�̗��ە�dA��dB�̔䗦�����߂郋�[�������߂���ƍl���Ă悢�B
�c��Ȑ��̓d�͗��p�҂����鎞�_�ɕۗL����d�C�@��̃X�C�b�`���u�I���v�ɂ���Ƃ����s���́C�d�͉�Ђ��猩��Ί��S�Ƀ����_���Ȏ��ۂł���B���������āu�I���v�Ƃ��������_���ȃV�O�i���ɑ��ċ��d�w�߂������ɂ́C�m���I�Ȏ��ۂ�\������Ƃ������@���̗p������Ȃ��B���̂悤�ȃP�[�X�ł̓x�C�Y�m���𗘗p����̂��L���ł���B�����Ŏ��̂悤�ȒP���ȃ��f���ɂ���āC��Ƃ��邢�͉ƌv�����鎞�_���������ł͑��d�����ł����G���鎞�_����鄟���ŁC�X�C�b�`���I���ɂ��ēd�̓l�b�g���[�N�Ɛڑ�����m�������߂�B
�܂����v�Ƃ͊�ƂƉƌv�̂Q��ނȂ̂ŁC���҂̓d�C�@��ۗL�ʂ�kW���ő���C���̔䗦���l����B�Ꭶ�I�ɂ��̔䗦��70����30���Ƃ��Đ������悤�B���ɑ��d�����G���ɗ��҂��@����u�I���v�ɂ��邻�ꂼ��̊m�����ߋ��f�[�^��͂ɂ���ĉ��\�̂悤�����C���ŗ^�����Ă���Ƃ���B
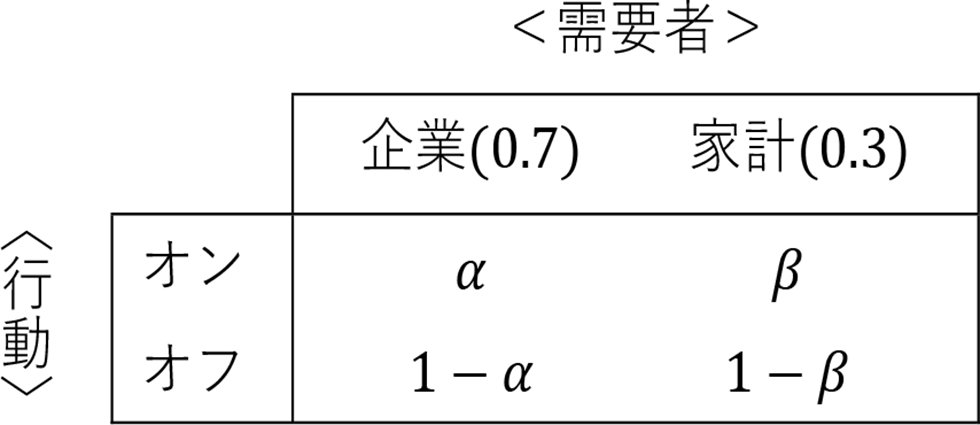
���̂悤�Ȋm����^������ƁC���d�������G���Ă���Ƃ��C��ƂƉƌv�̂��ꂼ�ꂪ�S�̂̋��ʐݔ��ɂ����ċ@����I���ɂ��Ă���x�C�Y�m�����v�Z���邱�Ƃ��ł���B���d�������G���Ă���Ƃ������_�ŗᎦ�I�f�[�^����\�ŗ^������C���̂Ƃ���ƂƉƌv�Ƃ��I���ɂ��Ă���m��k�̓x�C�Y�m����p����

�ƌv�Z�ł���B
�Ⴆ�Έ��Ƃ����� = 0.9,��= 0.5�Ƃ��Ă݂悤�B�s�[�N���Ɋ�Ƃ̋@���90�����ғ����C�ƌv�ł�50�����ғ����Ă���Ƃ���B�㎮�ɂ��Ă͂߂�Ƃ��ꂼ��̃x�C�Y�m����0.81��0.19�ƂȂ�B���̗�ł�kW�����猩�đ��ΓI�ɂ�葽���̋@���ۗL�����Ƃ�90���I���ɂ��Ă���̂ɑ��āC�ƌv�͋@��ۗ̕L�䗦���������I���Ƃ���m����50���ł���Ɖ��肵�Ă���B���d���̍��G�������炷�����̓x�C�Y�m���Ōv�Z�����u�I���v�̔䗦�Ŕ��肷��Ƃ������ꂩ��͊�Ƃ͖�81���̗����Ă��Ă��̕����S������ׂ��ƌ��邱�Ƃ��ł���B�܂肱�̃��f������C�e���v�҂����ʔ�̉��p�[�Z���g�S���ׂ����Ƃ������Ƀx�C�Y�m���ɂ���ē����邱�Ƃ��ł���B
�y243�Łz��ƂƉƌv�̊Ԃŋ����s�������݂Ă��������s��v�ɏI������Ƃ��̊e�����҂̎�����dA�CdB�ł���B���ꂾ���̊z���o������Ƃ��āC��ƂƉƌv�͋������č��v�����pG���ő剻����Ƃ����Q�[���ɗՂށB
�����Ńi�b�V�����������߂�Ƃ�������
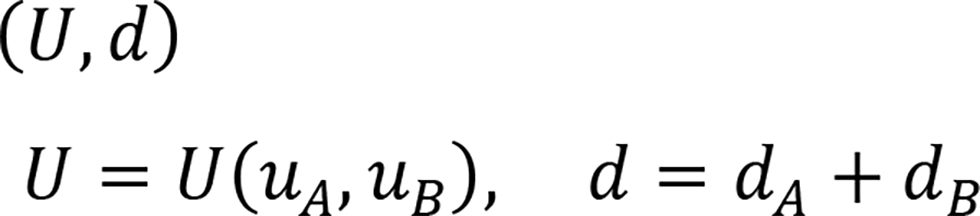
�ŕ\�����B
���̂Ƃ��̐��������
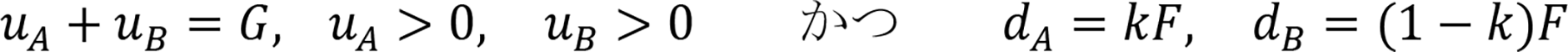
������k�͑O�߂œ��������x�C�Y�m���ł���C����ɂ����F��z�����Ă���B
����uA��uB�̎������ɉ����āC�i�b�V���������̃i�b�V���ς̍ő剻�ɂ���ċ��߂�B
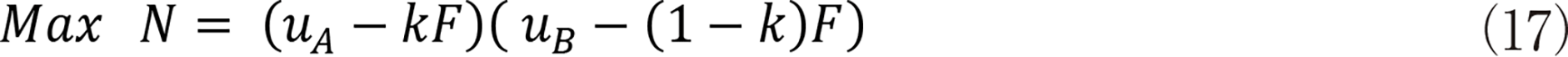
���̖���������
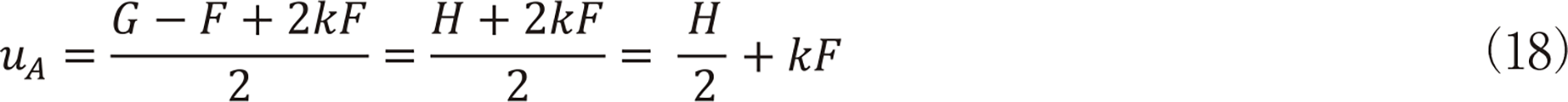

�ƂȂ�B
���������Ċ�ƂƉƌv���������ď���җ]��G���ő剻����Ƃ����Q�[�����v���C����C�ǂ���̃v���C���[�ɂƂ��Ă��ŏ��̎�����kF���邢�́i1−k�jF���H/2���������͑�����B���i��PA��F�Ƃ����������V�F�A�������H/2�����傫���������Ώ̓I�Ɏ�������B�ܘ_���̍��v�zH�́C���v���Ƃł͊�{���Ȃǂ̒�z�x�����Ƃ��Đ�������Ă���B����������H���x�������Ƃ�F���傫��G�Ƃ����]�肪�����ł��C�x�[�X���v�ł͕��ϔ�p���i�i�Ɉ������E��p�ŃT�[�r�X�𗘗p���邱�Ƃ��ł���悤�ɂȂ�B
���̃i�b�V�������͎v�l����������C��ƂƉƌv�����̂悤�ɍs������Ƃ����ۏ͂Ȃ��B�܂苦������Η�����������Ƃ������Ƃ̏\�������ɉ߂��Ȃ��B
�������Ȃ��猻���̌��v���Ƃ̗������������ƁC���E��p�����Ɗ�{���i�Œ�`���[�W�j�̒����Ƃ����Q�������ɂ���ăi�b�V�������̍l�����Ɠ����̂��Ƃ����j�I�Ɏ��{����Ă����B�܂茻��̒m�b�������z���̌�������⏕����������ʂ����Ă����̂ł���7�j
�ȏ�̕��͂��瓾�����v���e�͎��̂悤�ɂ܂Ƃ߂���B
�P�j�m���I��������ύt
�W�c�I�ȋ�������̓����́C��ʂ̃T�[�r�X���p�������_���ɔ������邱�Ƃ��琶������v�̓�d�\���ł���B������x�[�X���v�ƃs�[�N���v�i�d�͂ł���x�[�X�E���[�h�ƃs�[�N�E���[�h�j�ɕ�����Ƃ��C�s�[�N���v�͓����ݔ����������p���Ă���̂Ńx�[�X���v��O��Ƃ��Ă̂ݐ�������B
���̂Ƃ��ݔ��͑�K�͂ő傫�ȌŒ��K�v�Ȃ��Ƃ���C���Y�E����K�͂���������Ό��E��p�͕��ϔ�p���͂邩�ɏ������B���҂̘������傫���Ƃ��C���E��p�ŗ��������Č����I�Ȏ����z�����������悤�Ƃ���ƁC�傫�ȐԎ�����������B���̐Ԏ�������������o�[���P�l������x�����\�Ȕ͈͂ŕ��S���ĕ�U���邱�Ƃ��ł���Ή��}�̂悤�ȃx�[�X�ƃs�[�N�̂Q���_�Ŋm���I�ɋύt��B���ł���B
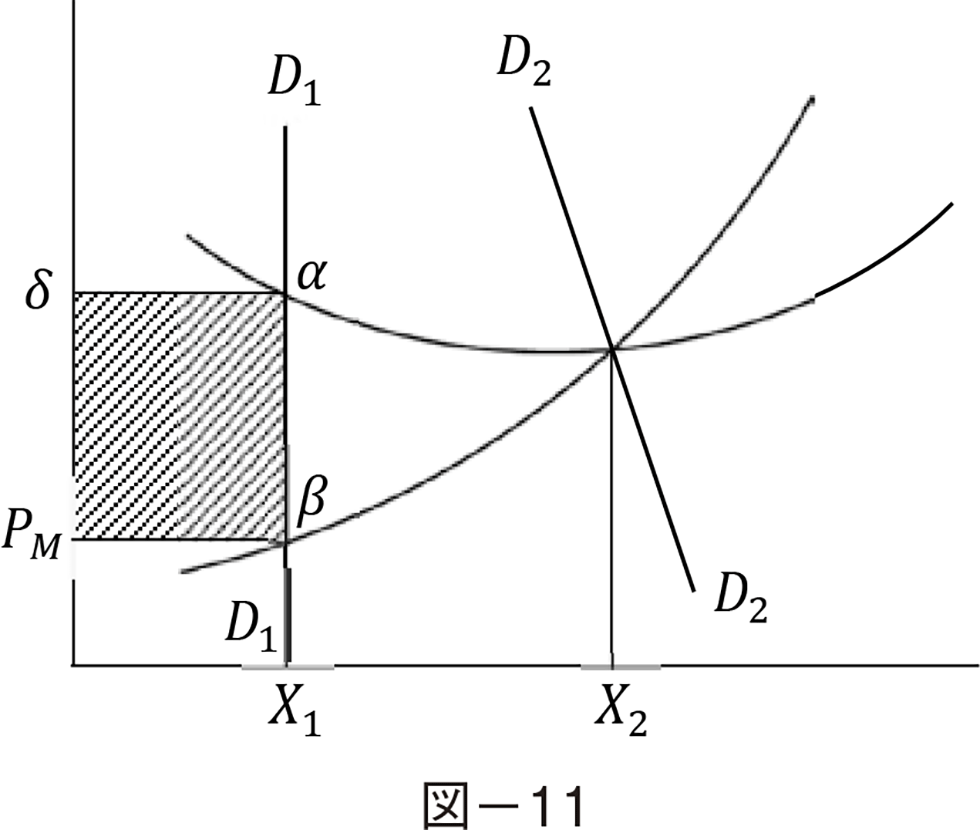
�x�[�X���vD1 D1�i�����ł͎��v�Ȑ��𐂒��Ƃ��Ă���j�ƃs�[�N���vD2 D2�ƌ��E��p�̌�_X1��X2�Ŏ����͋ύt���邪�CD1 D1�ł�����PM�����̐Ԏ���������BD2 D2�͏��^�̐ݔ��K�͂ɂ�����ڕW���Ɠx��B�����C�����͌��E��p����ѕ��ϔ�p�ɓ������B
���p�ҊԂ̋�������������ΐԎ������U���邱�Ƃ��ł���B�i�b�V�������ł͌��s��v�_�̃��f�������C�����̎��Ó��������E����B�{�e�ł͕��ϔ�p���i�̗^�������җ]����x�C�Y�m���ɂ���Ĕz������Ƃ����A�C�f�A������B���ʔ�ł��鑗�d���̃s�[�N���ɂ������ƂƉƌv�̗��p���̔z�����x�C�Y�m���ɂ���Č��肷��C���B�N���[�ȗ��̋��ʔ�z���̜��Ӑ���r���ł���B���p�ҊԂ̋����ɂ���ē������ݕ⏕���\�ƂȂ�\��������^���邱�Ƃ��ł����B
�Q�j���̕��͂ł͊m���I�ȋ�������ɏœ_�āC�������͊m���I���v�̕ϓ��Ƀ}�b�`����Ƃ������Ƃ�O��Ƃ��Ă���B����͓d�͂ɂ��Č����C�d�̓V�X�e�����v�ȑO�̓d�͉�Ђɋ����`�����ۂ����Ă����̃V�~�����[�V�����ƌ����Ă��悢�B�d�͎��R�����y245�Łz ��͋����`�����P�p���ꂽ�̂ŁC��q�̂悤�Ȏ����ύt�͎�X�̎s��̑n�݂Ɠ��D���x�ɂ���ĉ��������݂��Ă���B�������ݕ⏕�͓������ꂽ���{�̌Œ��̉����ۏႷ����̂�����C����ɑ�ւ���ɂ͑n�݂��ꂽ�s��̋@�\������I�������\�ɂ���悤�ɓ����K�v������B���������݂܂ł̂Ƃ���C�e�ʎs��ł͓��D���i�����肳���邱�Ƃ���������I�ȓd���������m�ۂł��邩���s�����ł���C���\���d�����x����Ă���Ă͂��邪�@�\���Ȃ��܂܍Č�������Ƃ����悤�ȏ������Ă���B�m���I�Ȑ��i������������T�[�r�X�ɂ��āC�ڕW�Ƃ��ׂ��͌��E��p�ɂ�鎑���z���������ɒB�����邩�ł���B���x�Ƃ��Č����I�Ȏs���v���鎎�݂ł́C����̃V�X�e�����v�ɉ��������Ă��邩���c�_���Ȃ���Ȃ�Ȃ��B
�R�j�m���I�ɕϓ�������v�Ƀ}�b�`���O���鋟��−������u�������ʁv�ƌĂ��−�ɂ͂ǂ̂悤�ɓw�͂��Ă����ԍ���������B���ꂪ�}−�V�Ŏ�������t�Ƃ����ʑ��̂���ł���B�ʑ��̂���͓d�͂Ɍ��炸�W�c�I��������ł͂ǂ̃T�[�r�X�ɂ��Ă����݂���B�{�e�ł���ɂ��ė�������Ȃ������̂́C�����{�i�I�ɕ��͂���ɂ́C���f����O�ςƂ����T�O�����Ȃ���Ȃ�Ȃ�����ł���8�j�B�����𗘗p�ł���ƁC���́u���b�v�Ƃ����T�͂�苭�͂ȃc�[���ƂȂ�B�����ĊO����قȂ�悤�Ɍ�����^�A�T�[�r�X�ł��C�W�c�I��������̈�p�̒n�ʂ��߂邱�Ƃ��ł���B
�S�j�������ݕ⏕�ɂ�����Ԏ���U�Ƃ����H�v�́C���v���Ƃ̗��j�ɂ����Ắu���[�g�E���C�L���O�v�Ƃ������̉���100�N�߂��O����_�����Ă������̂ł���B19���I��������v���ƃT�[�r�X�������ɕ��y�����邽�߂ɂ́C�P����̎g�p�����i���E������j���ł������������邱�Ƃ��s��̊J���ɕK�{�ł������B�����ŏW�c����ɉ����i�T�u�X�N���C�u�j���錠�������邢�͕ۏ؋��Ƃ��āC��{���Ȃǂ̈ꊇ�ꎞ������������������C���݂ɑ���܂ő������Ă���B���R���ɂ���Ēn��Ɛ�`�Ԃ͉������ꂽ�Ƃ��Ă��C�P����̗��p������Ⴍ����H�v�Ƃ��Ă���͗L���ł���B���ۍŋ߂̃g�����h�Ƃ��ė��s���Ă���u�T�u�X�N�v�Ƃ����x�������@�́C�Ώۂ������I�ȃT�[�r�X�Ƃ͈قȂ�Ƃ͌����C�����ȏ��i���w�������P�����y���ނƂ����ړI�Ől�C������B�܂�C�o�ϕ��͏�͗��ۉ��i���ƐԎ����Ƃ����`�i�O�o�i11�j�����邢�́i13�j���j�Ř_�������C���̏��������������͈ӊO�ɑ����C�����ɑ��݂��Ă���B
Armstrong, M and J.Vickers�i2001�j, �gCompetitive Price Discrimination.�h Rand Journal of Economics, 32�i4�j:579-605.
������ �i2010�j �hCompetitive Non-Linear Pricing and Bundling.�h Review of Economic Studies, 77�i1�j: 30-60.
Coase, Ronald H. �i1946�j. �hThe Marginal Cost Controversy.�h Economica, 13�i51�j: 169-82.
Hotelling, Harold�i1938�j. �gThe General Welfare in Relation to Problems of Taxation and of Railway and Utility �y246�Łz Rates.�h Econometrica, 6�i3�j: 242-69.
Frischmann, Brett M. and Hogendorn, Christiaan�i2015�j. �gThe Marginal Cost Controversy.�h Journal of Economic Perspectives, 29�i1�j: 193-206.
Vickrey, William �i1948�j. �gSome Objections to Marginal Cost Pricing.�h Journal of Political Economy, 56 �i3�j: 218-38.
�F��O���i1994�j�w�Љ�I���ʎ��{�����R�����Y�Ɠs�s�x�i�F��O���E�Ζ؈���Y�ҁ@������w�o�ʼn�C1994�N�j��P�� �Љ�I���ʎ��{�̊T�O pp.15-45
���c�́i2021�j�w�Q�[�����_ ��R�Łx�@��W�́@�Q�l�����
�k�v��i1974�j�w���v���Ƙ_�x�i���m�o�ϐV��Ёj
�암�ߕF�i1983�j�w���{�̌���Ɓx�i����s�G�E�A���v�ғ�����w�o�ʼn�j��R�͉��ipp.66-78
�������i1994�j�w�F��E�ΖؑO�f���x��Q�́u���v���Ƃ̊T�O�ƎЉ�I���ʎ��{�vpp.47-69
�������i2010�j�u�Љ�I���ʎ��{�Ƃ��Ă̎����\�Ȉ�ÃV�X�e���v�ی���ÉȊwvol.59,No.1,pp.2-9
�������i2022�j�u�o�ϊw�̎��_���猩���d���C�w�̓d�ꃁ�J�j�Y���v�w�K�@��w�o�ϊw�_�W�@��59���R��
�������i2025���s�\��j�u�W���I��������T�[�r�X�Ƃ��Ắu���v���Ɓv�����d�͎Y�Ƃ̎������J�j�Y���v�i����j